Match List I with List II and select the correct answer using the codes given below the lists :

A
abcdsrpq
B
abcdqsrp
C
abcdsrpq
D
abcdqspr
Text Solution
The correct Answer is:A
tan−1(12x+1)+tan−1(14x+1)=tan−1.2x2
⇒tan−1(3x+14x2+3x)=tan−1.2x2
⇒3x2−7x−6=0
⇒x=−23,3
But for x−23, L.H.S is negative and R.H.S. is positive
Hence, the only solution is x=3
Note : Solution of the remaining parts are given in their respective chapters
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Solved Examples And Exercises
231 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank
24 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - JEE Main Previous Year
2 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year
20 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
Similar Questions
Knowledge Check
Match List I with List II and select the correct answer using the code given below the Lists :
 APQRS3412BPQRS1243CPQRS3321DPQRS2314
APQRS3412BPQRS1243CPQRS3321DPQRS2314
Match List I with List II and select the correct answer using the code given below the lists

View SolutionMatch List I with List II and select the correct answer using the code given below the lists:

View SolutionMatch List I with List II and select the correct answer using the code given below the lists:

View SolutionMatch List I with List II and select the correct answer using the code given below the lists:

View SolutionMatch List I with List II and select the correct answer using the code given below the Lists :
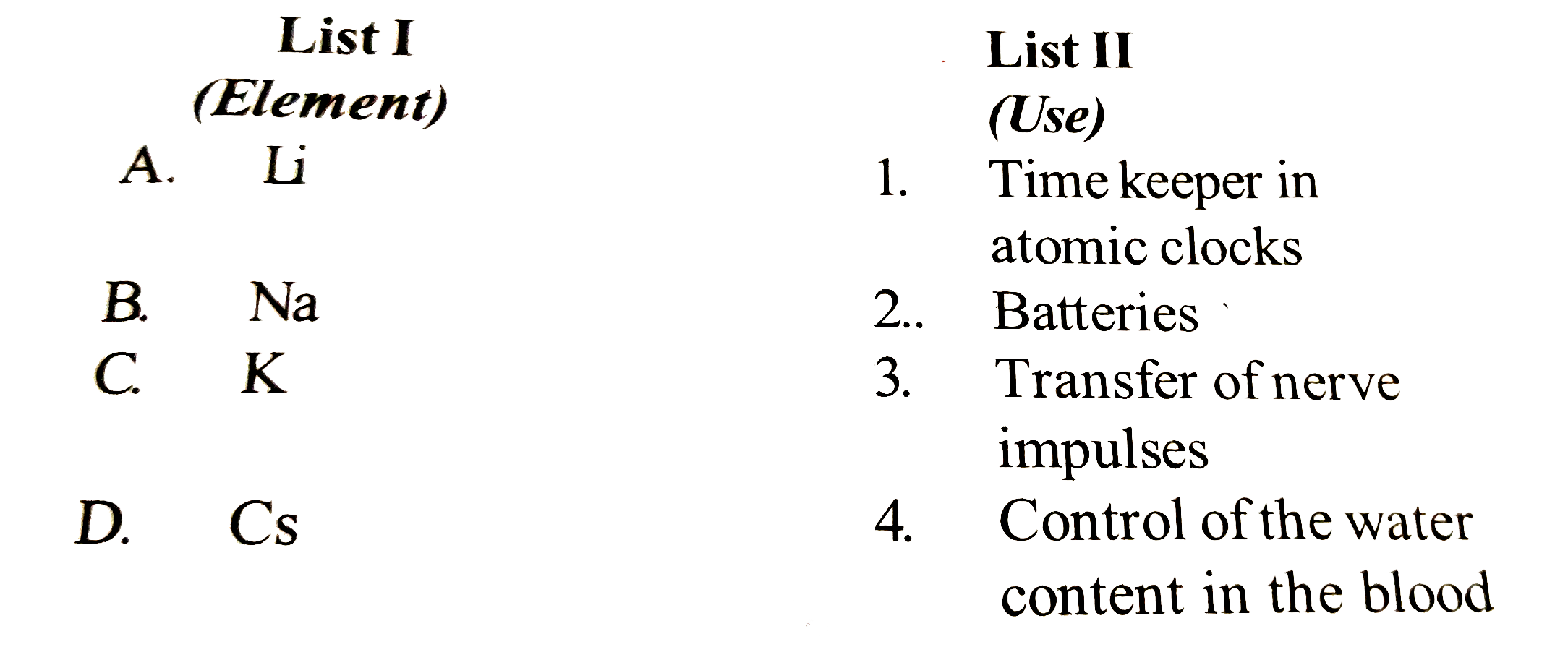
View SolutionMatch list I with List II and select the correct answer using the code given below the lists

View SolutionMatch List I with List II and select the correct answer using the code given below the Lists:

View Solution


