Complete Solutions to Solved Examples of chapter CAPACITOR AND CAPACITANCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CAPACITOR AND CAPACITANCE |
| CENGAGE PHYSICS | Solved Examples |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
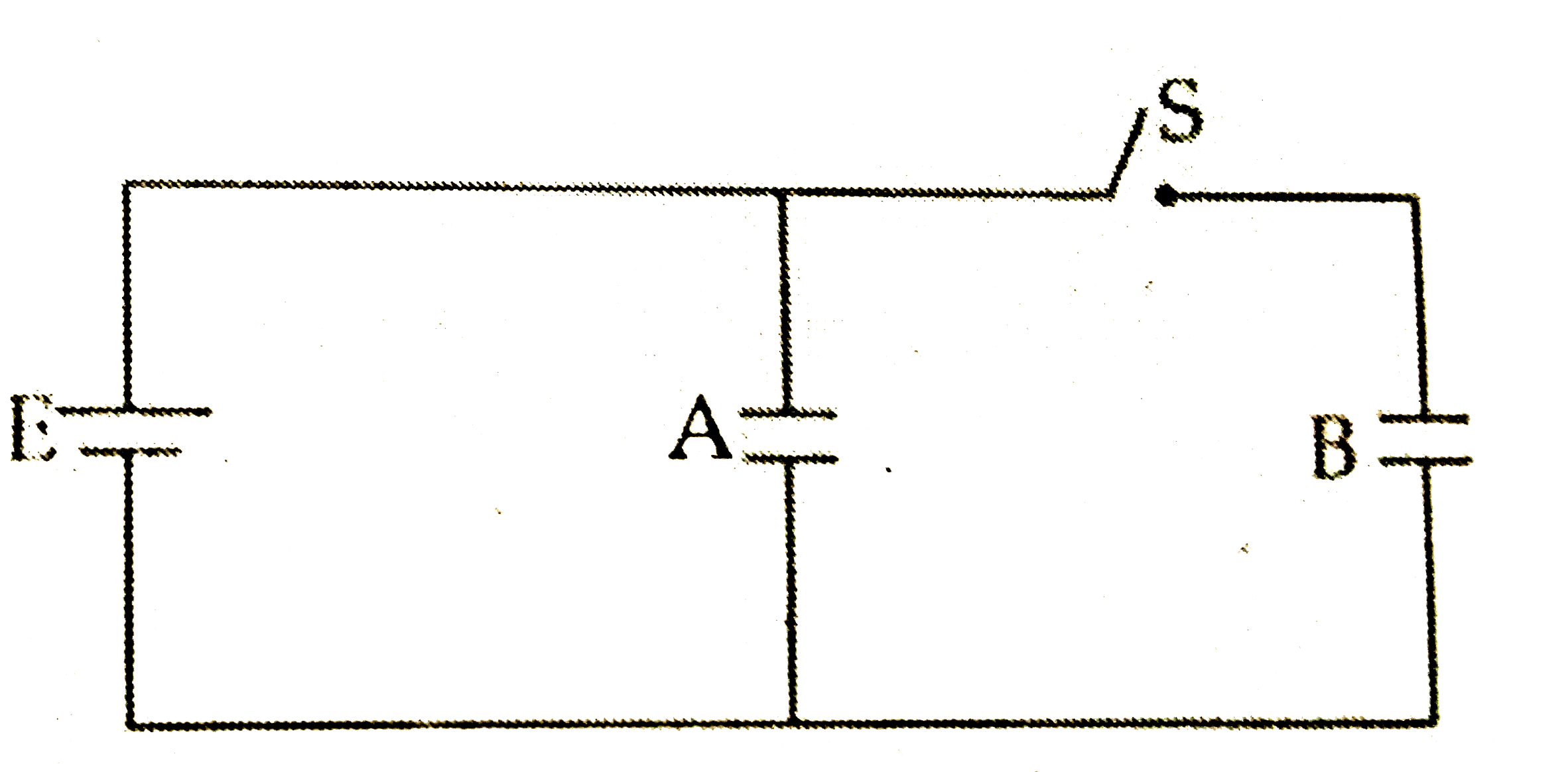
Two identical parallel plate capacitors A and B are
connected to a battery of V volts with the switch S
closed . The switch is now opend and the free
space between the plantes of the capacitors is filled
with a dielectric of dielectric constant K. Find the
rario of the total electrostatic energy stored in both
capacitors before and after the introduction of the dielectric.
View SolutionTwo parallel plate capacitors of capacitance C each are connected in series with a battery of emf `epsilon`. Then, one of the capacitors is filled with a dielectric of dielectric constane K.
i. Find the change in electric field in the two capacitors, if any
ii. What amount of charge flows through the battery?
iii Find the change in the energy stored in the circuit, if any.
View SolutionFive identical conducting plates, `1, 2,3,4` and `5` are fixed parallel pltes equidistant from each other (see figure). A conductor connects plates 2 and 5 while another conductor joins 1 and 3. The junction of 1 and 3 and the plate 4 are connected to a source of constant emf `V_0`. Find

(a) the effective capacity of the system between the terminals of source.
(b) the charges on the plates 3 and 5. Given, `d =` distance between any two successive plates and `A = ` area of either face of each plate.
View SolutionTwo parallel plate capacitors A and B have the same separation `d=8.85xx10^-4m` between the plates. The plate area of A and B are `0.04m^2` and `0.02m^2` respectively. A slab of dielectric constant (relative permittivity) `K=9` has dimensions such that it can exactly fill the space between the plates of capacitor B.
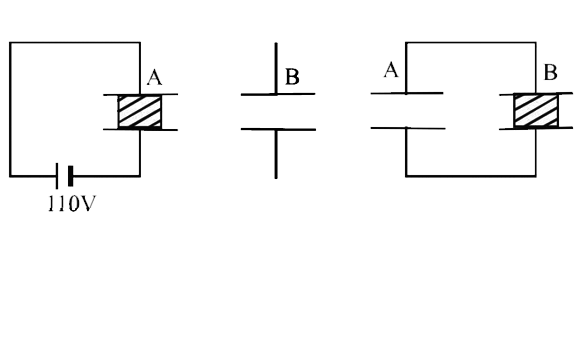
(i) The dielectric slab is placed inside. A as shown in figure (a). A is then charged to a potential difference of 110V. Calculate the capacitance of A and the energy stored in it.
The battery is disconnected and then the dielectric slab is moved from A. Find the work done by the external agency in removing the slab from A.
(iii) The same dielectric slab is now placed inside B, filling it completely, The two capacitors A and B are then connected as shown in figure(c). Calculate the energy stored in the system.
View SolutionTwo capacitors A and B with capacities `3 muF` and `2 muF` are charged to a potential differece of `100 V` and `180 V`, respectively. The plates ot the capacitors are connected as shown in, with one wire free from each capacitor. The upper plate of A is positive and that of B is negative An uncharged `2muF` capacitor C with lead wires falls on the free ends to complete the circuit.
i. Calculate the final charge on the three capacitors,
ii. Find the amount of electrostatic energy stored in the system before and after the completion of the circuit.
 .
.
View SolutionIn the circuit shown , the emf of each battery is `60 V` and `C_(1)=2 muF` and `C_(2)=3 muF`. Find the charges that will flow through the sections `1 , 2` and `3` after the Key is closed.
 .
.
View SolutionFind the capacitance between the terminals `A` and `C_(3)` If `epsilon_(r) = 2`
View SolutionTwo parallel plate capacitors differ only in the spacing between their (very thin) plates , AB has a spacing of `5` mm and a capacitance of `20 pF`, while CD has a spacing of `2 mm` . Plates `A` and `C` carry charges of `+1 nC`, while B and D each carry `-1 nC`, What are the potential diffences ` V_(AB)` and `V_(CD)` after the capacitor `CD` is slid centrally between and parallel ot the plates of AB without touching them ? Would it make any difference if CD was not centrally paced between A and B ?
 .
.
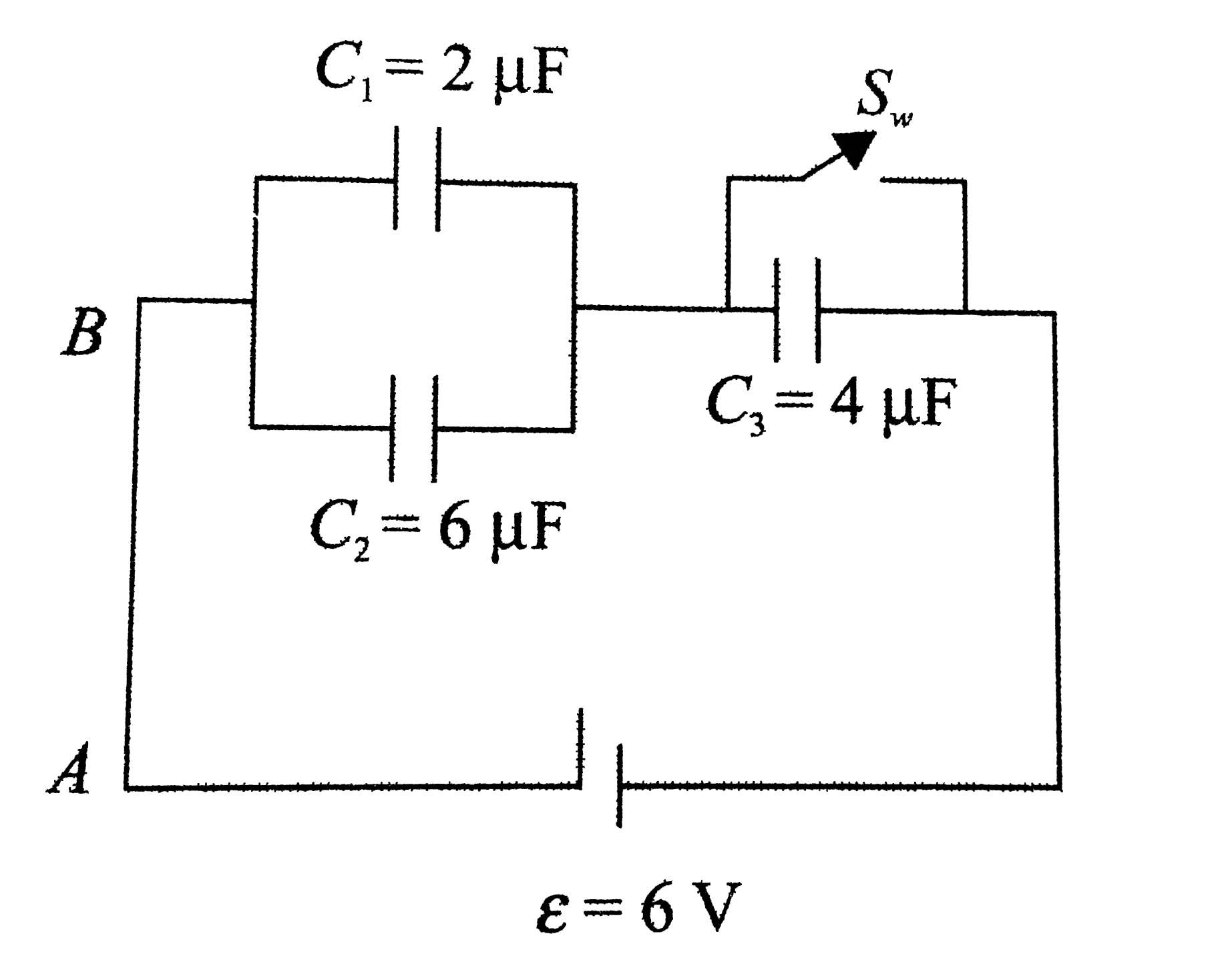
View SolutionIn, all the capacitors are in steady state initially.
i. What is the charge flowing through the switch when it is closed?
ii. What is the charge flowing section AB?
iii. What is the work done by the battery?
iv. What is the heat produced when (S) is closed?
 .
.
View SolutionIn the circuit shown in , capacitor A has capacitance `C_(1)=2 muF` when filled with a dielectric slab `(k=2)`. Capacitors `B` and `C` are air capacitors and have capacitaces `C_(2)=3 muF` and `C_(3)=6 muF`, respectively.
 .
.
A is charged by closing the switch `S_(1)` alone.
i. Calculate the energy supplied by the battery during the process of charging.
Switch `S_(1)`is now opened and is closed.
ii. Calculate the charge on B and the energy stored in the system when an electrical equilinrium is atained.
Now switch `S_(2)` is also opened, and the slab of A is removed. Another dielectric slab of `K=2`, which can just fill the space in B, is inserted into it and then switch `S_2` alone is closed.
iii. Calculate by how many time the electric field in B is increased. Calculate also the loss of energy during the redistribution of charge.
View Solution
Solved Examples questions and complete solutions for chapter CAPACITOR AND CAPACITANCE of CENGAGE PHYSICS (ENGLISH) of Class 12