Complete Solutions to MCQ s of chapter ELECTRIC FLUX AND GAUSS LAW of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC FLUX AND GAUSS LAW |
| CENGAGE PHYSICS DPP | MCQ s |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
Electric flux through a surface are `10 m^(2)` lying in the xy plane is `(ifvecE= hati + sqrt2hatj + sqrt3 hatk N//C)`
View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View SolutionA point charge q is placed near hemisperical suface without base, cylindrical surface with one end open sperical surface and hemispherical surface with base as shown in the figure in (a) (b) (c) and (d) respectively In wihich of the following cases m the flux crossing through the surface is zero ?

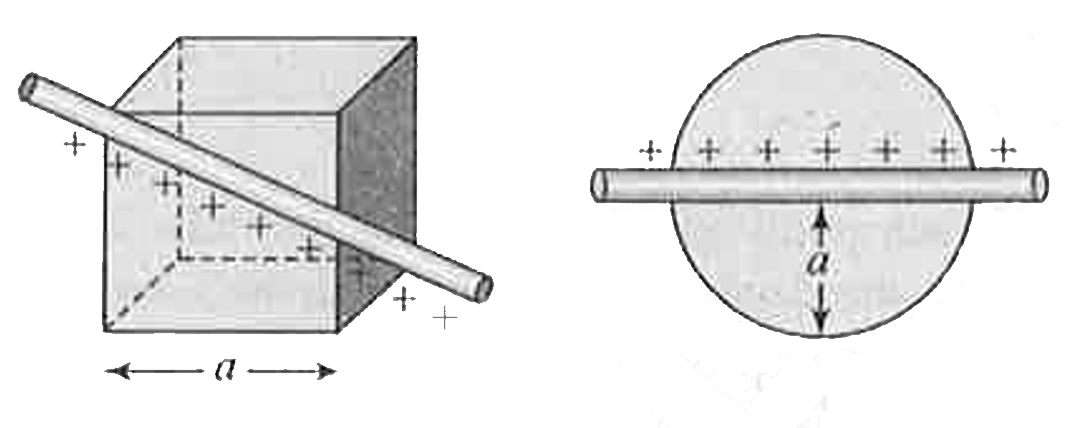
View SolutionA linear charge having linear charge density `lambda` penterates a cube diagonally and then it penterates a sphere diametrically as shown. What will be the ratio of flux coming out of cube and sphere ?
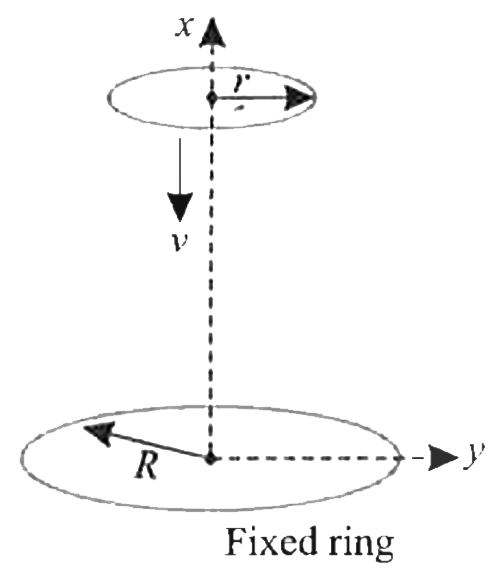
View SolutionA ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius `r(ltltR)` and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux `(phi)` passing through the smaller ring with position will be best represent by :
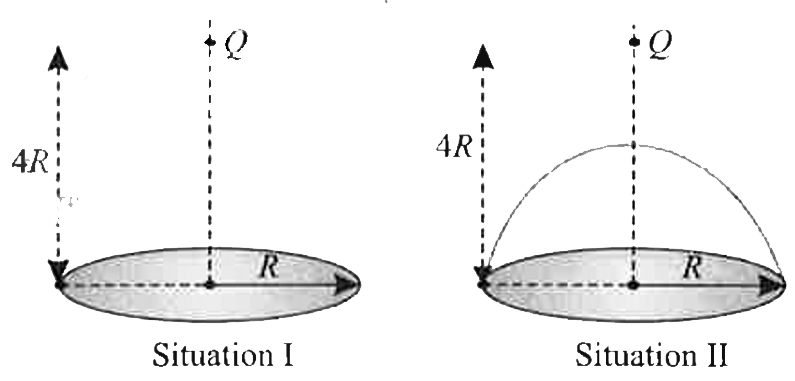
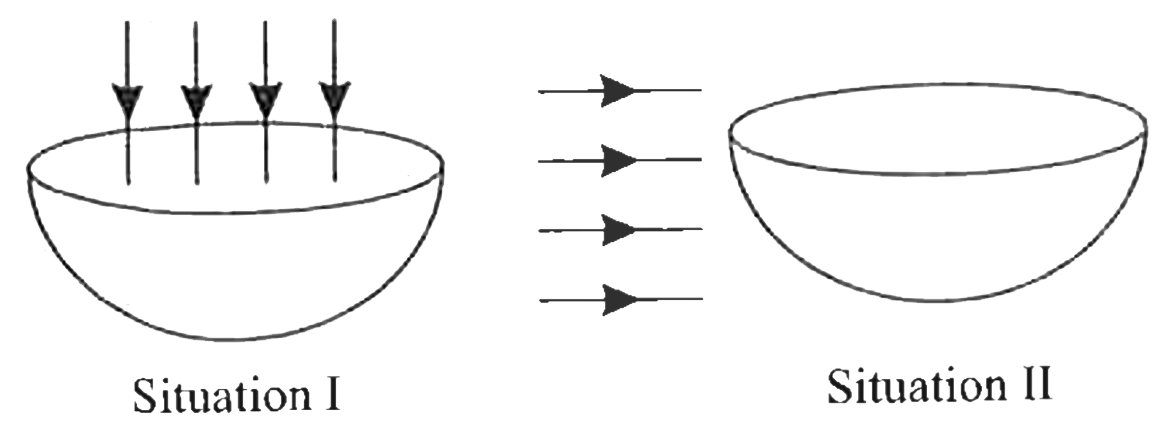
View SolutionA positive point charge Q is placed (on the axis of disc) at a distance of 4 R . Above the centre of a disc of radius R as shown in situation I. the magnitude of electric flux through the disc is `(phi)`. Now a hemis pherical shell of radius R is placed over the disc. such that it forms a closed surface as shown in situation II. The flux through the curved suface in situation II taking direction of area vector along outward normal as positive is
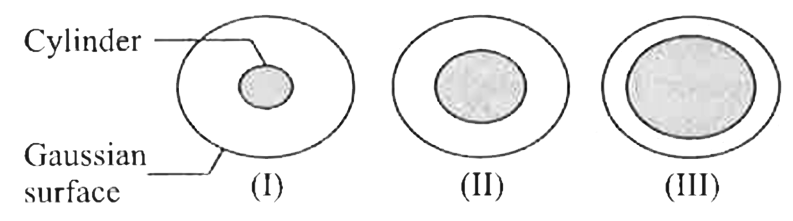
View SolutionFigure showns. In cross section m three solid cylinders, each of length L and uniform charge Q. Concntric with each cylinder is a cylindrical Gaussion surface, with all three surfaces having the same radius. Rank the Gussion surface according to the electric field at any point on the suface, greatest first.
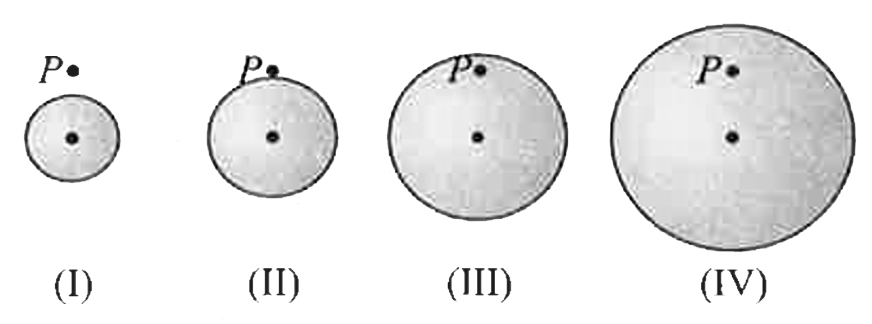
View SolutionFigure showns four solid spheres, each with charge Q uniformly distributed through its volume. The figure also shows a point P for each sphere. All at the same distance from the centre of the sphere. Rank the spheres according to the magnitude of the electric field they produce at point P.
View SolutionIn the figure a hemispherical bowl of bowl of radius R is shown Electric field of intensity E is present perpendicular to the circular cross section of the hemisohere.
View Solutionfigure shows, in cross section, two Gaussian spheres and two Gaussian cubes that are centered on a positively charged particle on a positively charged partical . Rank greatest first, and indicate whether the manitudes are unifrom or variable along each surface.
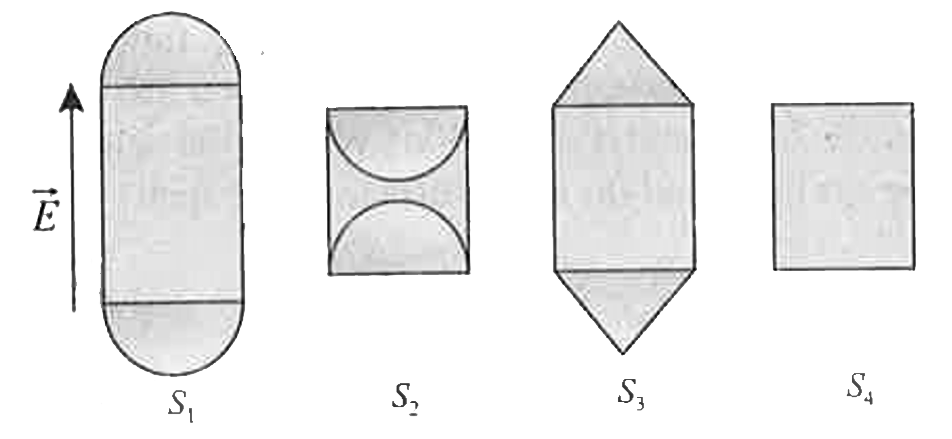
View SolutionFigure shows four Gaussion surfaces consisting of identical cylindrical midsections but different end caps. The surfaces central axis of each . Cylindrical midsection , the end caps have these shapes, `S_(1)` convex hemispheres `S_(2)` concave hermisphere `S_(3)` cones `S_(4)`e flat disks. rank the surfaces acccording to (a) the net electric flux through them and (b) the electric flux through the top end caps , greatest first.
View SolutionIn figure , a solid sphere of radius a = 2.00cm is concentric with a spherical conductiosn shell of inner raedius b =2.00 a and outer radius c=2.40 a. the sphere has a net unifrom charge `q_(1)=+5.00C`. The shell has a net charge `q_(2) =-q_(1)`. Distance (a) r=0 (b) r= a/2.00 (c) r=a (d) r = 1.50 a (e) r= 2.30a and (f) r= 3.50 a ? what si the net charge on the (g) inner and (h) outer surface of the shell ?
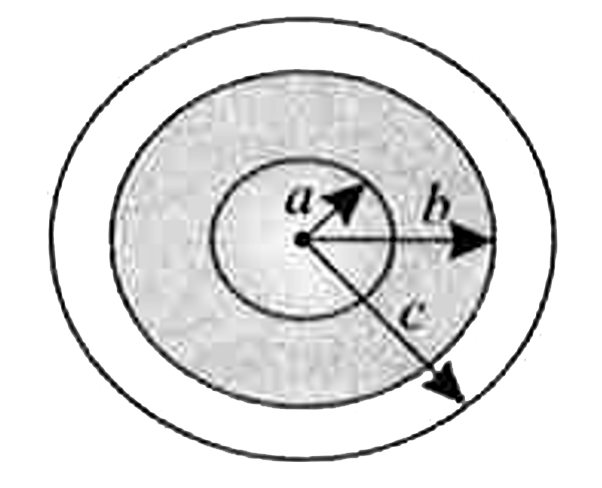
View SolutionA uniform charge density of `500 nC//m^(3)` is distributed throughout a spherical volume of radius 6.00cm .Consider a cubical Gussian surface with its center at the centre of the sphere. What is the elcetric flux through this cubical surface if its edge length is (a) 4.00cm and (b) 14.0 cm ?
View Solutionthe net electric flux through each face of a die (singular of dice) has a magnitude in units of `10^(3)N.m^(2)//C` that is exactly equal to the number of sport N on the face ( 1 through 6) the flux is inward for N odd outword for N even. What is the net charge inside the die ?
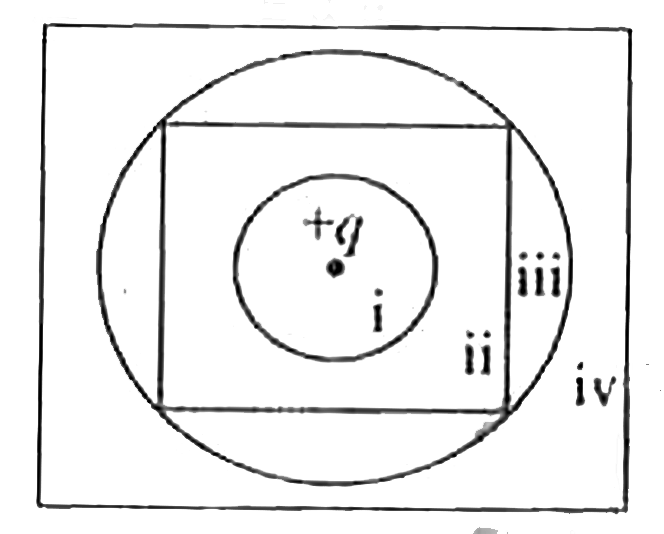
View SolutionA Gaussian surface S encloses two charges `q_(1)= q and q_(2) = -q`the field at p is
where `vecE_(1), vecE_(2)and vecE_(3)` are the field contributed by `q_(1),q_(2)and q_(3)at` P respectively.

View SolutionThe electric field in a region is radially outward with magnitude `E=Agamma_(0)`. The charge contained in a sphere of radius `gamma_(0)` centered at the origin is
View SolutionA charge q is placed at the centre of the open end of a cylindrical vessel . The flux of the electric field through the surface of the vessel is

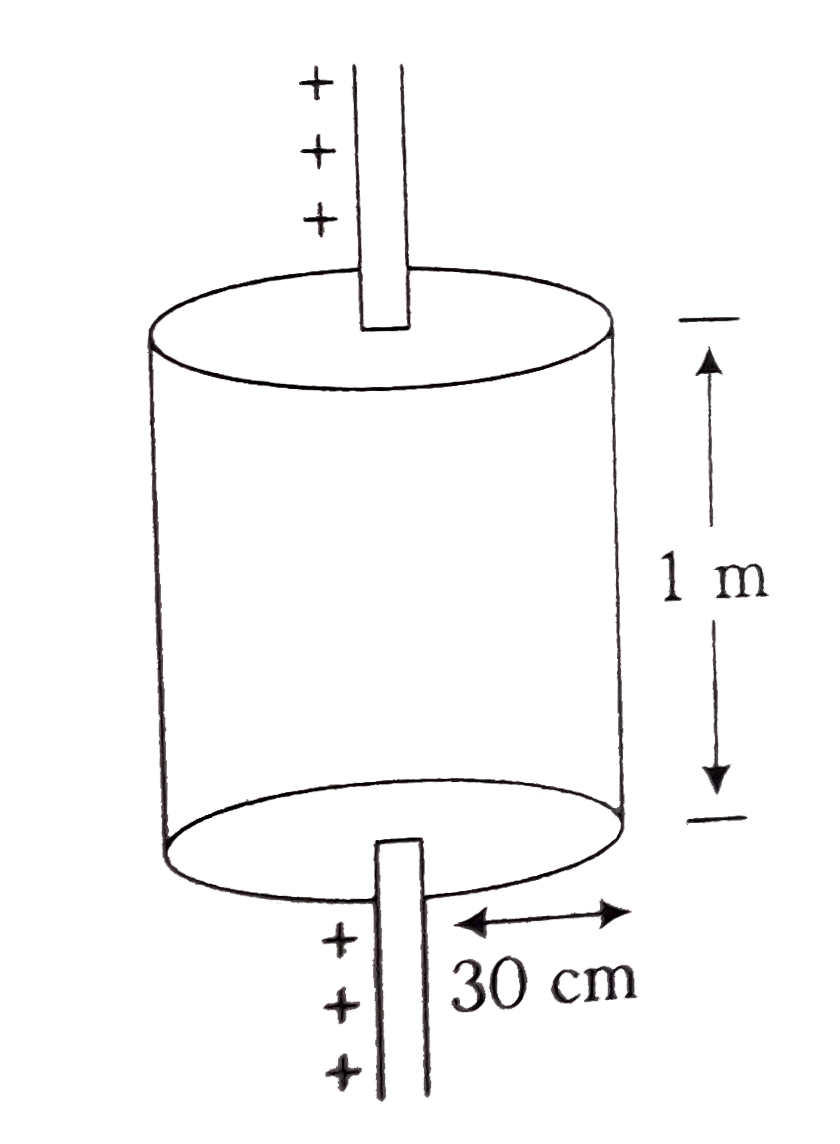
View SolutionElectric charge is uniformly distributed along a long straight wire of radius 1 mm. The charge per centimetre length of the wire is Q coulomb. Another cylindrical surface of radius 50 cm and length 1 m symmetrically enclosed the wire as shown in the figure. The total electric flux passing through the cylindrical surface is
View SolutionIn a region of space having a spherical symmetic distribution of charge , the electric flux enclosed by a concentric spherical Gaussion surface, varies with radius
`r" as "phi={(phi_(0)r^(2))/R^(3), r le R
phi_(0)`, `ltR` where R and `phi_(0)` are the constants.
View SolutionIn a region of space the electric field in the `x`-direction and proportional to `x`i.e., `vec(E )=E_(0)xhat(i)`. Consider an imaginary cubical volume of edge a with its parallel to the axes of coordinates. The charge inside this volume will be
View SolutionFigure shows a closed dotted surface which intersects a conduccting uncharged shere. If a positive charge is placed at the point P, the flux of the electric field through the closed surface

View Solutionfigure shows a neutral metallic sphere with a point charge +Q placed near its surface. Electrostatic equilibrium conditions exist on metallic sphere. Mark the correct statement :

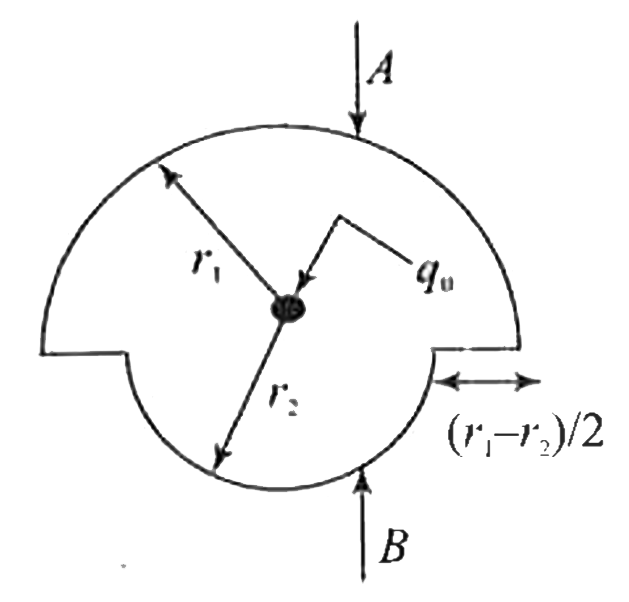
View SolutionA and B are semi - spherical surfaces of radius `r_(1)and r_(2) (r_(1) lt r_(2)) with E_(1) and E_(2)` as the electric fields a the their surfaces. Charge `q_(0)` is placed as shown. What is the condition which may be statisfied ?
View Solutionthe electric field intensity at all points is space is given by ` vecE=sqrt3hati-hatj` volts/meter. A square frame LMNO of side 1 meter is shown in the figure. The point N lies in x-y plane. The initial angle between line ON and x -axis is `theta = 60^(@)`
the magnitude of electric flux through area enclosed in square frame LMNO is
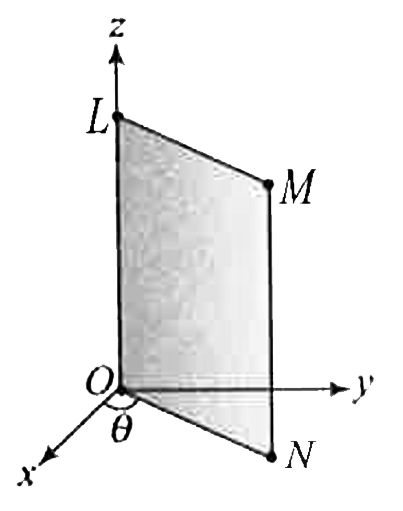
View Solutionthe electric field intensity at all points is space is given by ` vecE=sqrt3hati-hatj` volts/meter. A square frame LMNO of side 1 meter is shown in the figure. The point N lies in x-y plane. The initial angle between line ON and x -axis is `theta = 60^(@)`
The work done by electric field in taking a point charge `1muC` from origin O to point M is
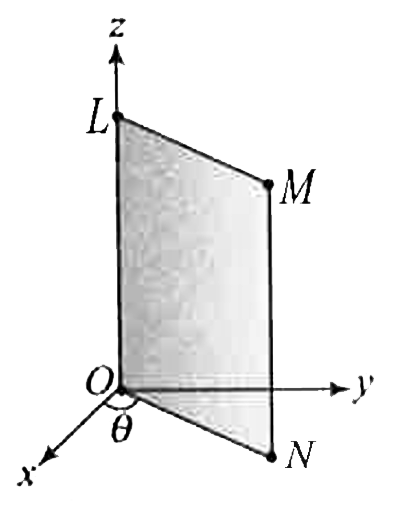
View Solutionthe electric field intensity at all points is space is given by ` vecE=sqrt3hati-hatj` volts/meter. A square frame LMNO of side 1 meter is shown in the figure. The point N lies in x-y plane. The initial angle between line ON and x -axis is `theta = 60^(@)`
the magnitude of electric flux through area enclosed in square frame LMNO is

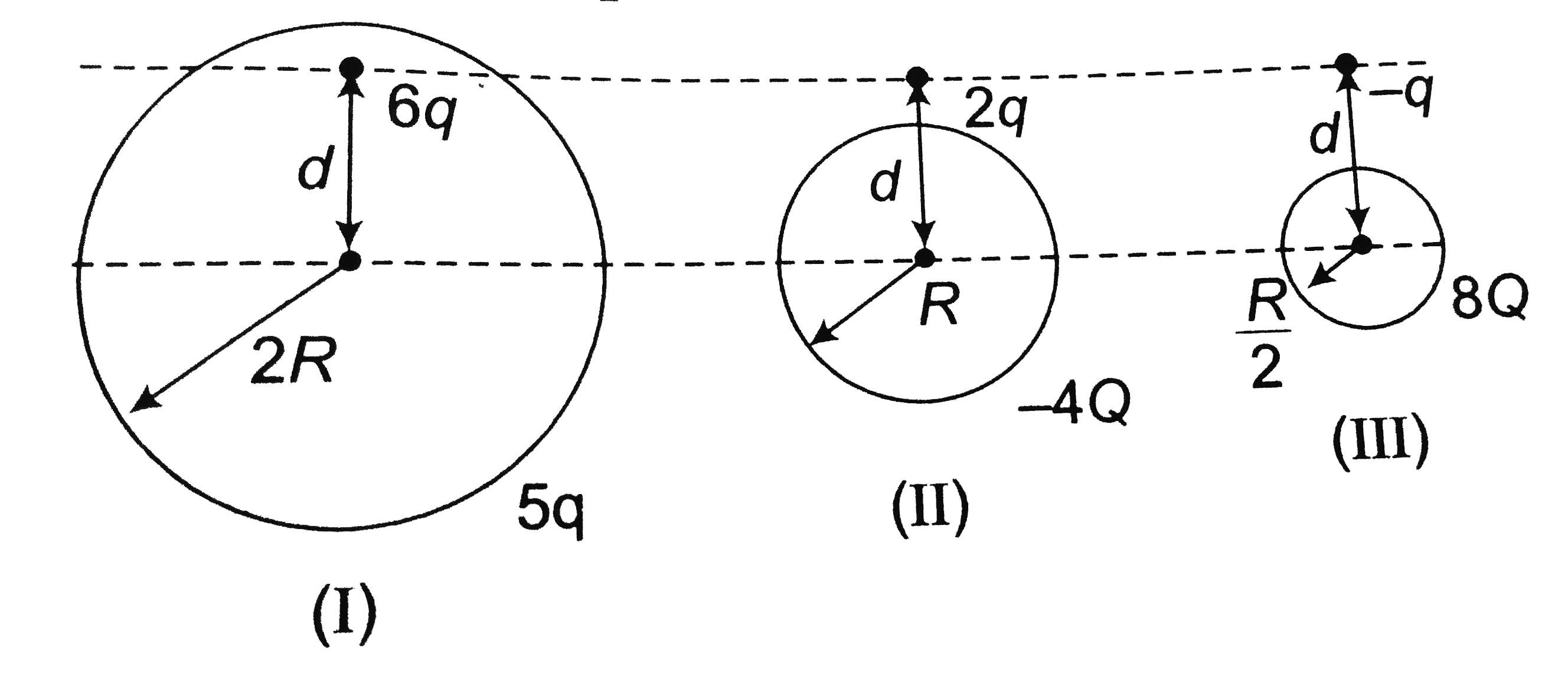
View SolutionFigure, shown above, shows three situations involving a charged particle and a uniformly charged spherical shell. The charges and radii of the shells are indicated in the figure. If `F_(1),F_(2)` and `F_(3)` are the magnitudes of the force on the particle due to the shell in situations (I),(II) and (III) then
View SolutionThere are three concentric thin spheres of radius `a,b,c (agtbgtc)`. The total surface charge densities on their surfaces are `sigma,-sigma,sigma` respectively. The magnitude of the electric field at `r` (distance from centre) such that `agtrgtb` is:
View SolutionThe electric field inside a sphere having charge density related to the distance from the centre as`rho=alpha r` (`alpha` is a constant) is :
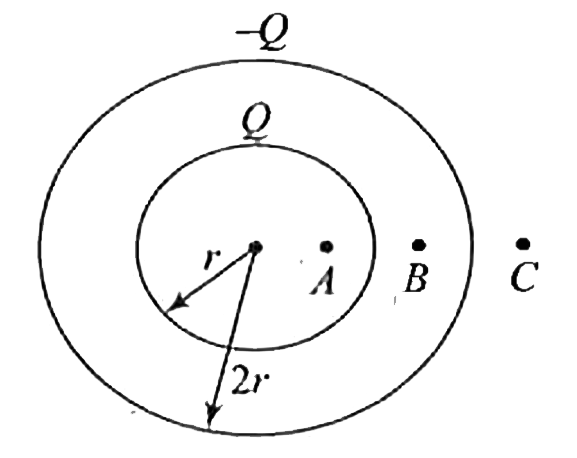
View Solutionconsider two thin unifromly charged concentric shells of radii r and 2r charges Q and -Q respectively , as shown. Three points A,Band C are marked at distances `r/2 , (3r)/2and (5r)/2` respectively from their common centre. If `E_(A) E_(B) and E_(C)` are magniudes of the electric fields at points A, Band C respectivly ,then
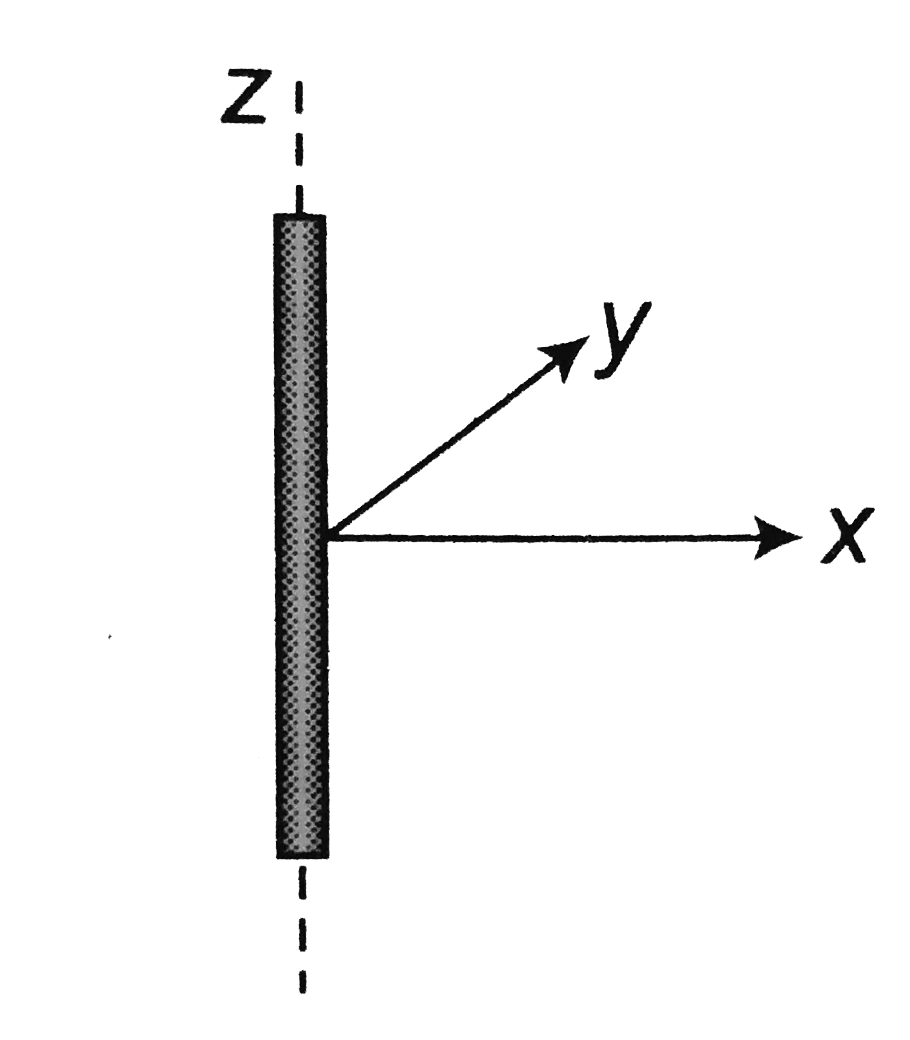
View SolutionAn infinitely long wire is kept along `z`-axis from `z=- oo` to `z=oo`, having uniform linear charge density `(10)/(9) nC//m`. The electric field at point `(6 cm,8cm,10 cm)` will be
View SolutionTwo conentric conducting thin spherical shells A and B having radii `r_(A)` and `r_(B) (r_(B) gt r_(A))` are charged to `Q_(A)` and `-Q_(B) (|Q_(B)| gt Q_(A)|)`. The electrical field along a line, (passing through the centre) is
View Solutiontwo large conducting thin plates are placed parallel to each other. They carry the charges as shown. The variation of magnitude of eclectric field in space due to this system is best given by
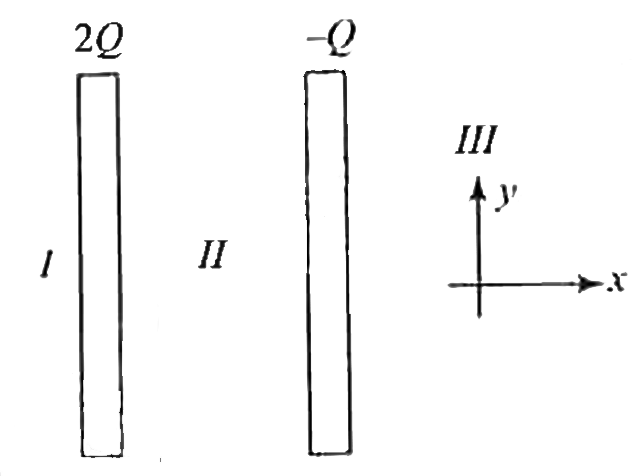
View SolutionA positively charge sphere of radius `r_0` carries a volume charge density `rho`. A spherical cavity of radius `r_0//2` is then scooped out and left empty. `C_1` is the center of the sphere and `C_2` that of the cavity. What is the direction and magnitude of the electric field at point B?

View SolutionThe absolute charge on an electron is -
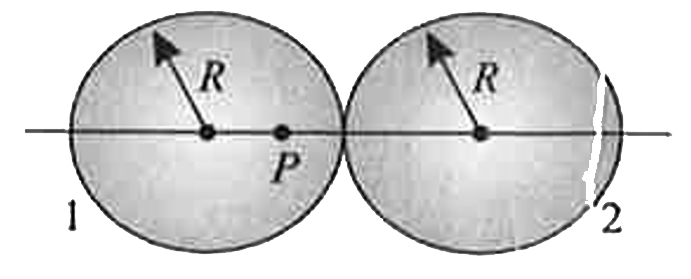
View Solutionfigure shows, in cross section, two solid spheres with uniformaly distributed charge throughout their volumes. Each has radius R. point P lies on a line connecting the centres of the spheres, at radial distance r/2.00 from the centre of sphere 1 . If the net electric field at point P is zero what is the ratio `q_(2)//q_(1)` of the total charges ?
View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density `sigma` . A very long uniformaly charged line charge( linear charge density `lambda`) is placed along the ctlinder axis. If electric field intensity vector outside the cylinder is zerom then :
View SolutionTwo infinte plane sheets A and B are shown in the figure the surface charge densities on A and B are `(2//pi) xx 10^(-9)C//m^(2) and (-1 //pi) xx 10 ^(-9)C//m^(2)` rospectively .C,D, E are three points where electric fields (in N/C) are `E_(C) , E_(D) and E_(E)` repectively.
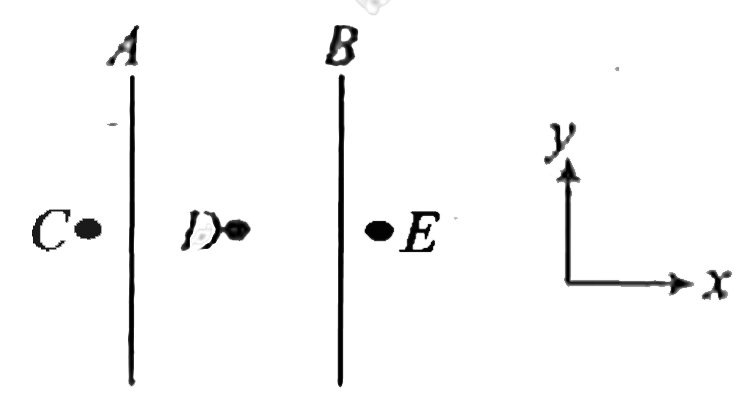
View Solution
MCQ s questions and complete solutions for chapter ELECTRIC FLUX AND GAUSS LAW of CENGAGE PHYSICS (ENGLISH) of Class 12