There are three concentric thin spheres of radius a,b,c(a>b>c). The total surface charge densities on their surfaces are σ,−σ,σ respectively. The magnitude of the electric field at r (distance from centre) such that a>r>b is:
0
σε0r2(b2−c2)
σε0r2(a2+b2)
none of these
The correct Answer is:b
To solve the problem of finding the electric field at a distance r from the center of three concentric spheres with surface charge densities σ, −σ, and σ on spheres of radii a, b, and c respectively (where a>b>c), we will use Gauss's Law.
1. Identify the Regions:
We have three concentric spheres:
- Sphere 1 (radius c): surface charge density σ
- Sphere 2 (radius b): surface charge density −σ
- Sphere 3 (radius a): surface charge density σ
We are interested in the region where b>r>c.
2. Apply Gauss's Law:
According to Gauss's Law, the electric field E through a closed surface is proportional to the charge enclosed by that surface:
ΦE=∮E⋅dA=Qencϵ0
Here, dA is the differential area element on the Gaussian surface, and Qenc is the total charge enclosed by the Gaussian surface.
3. Choose a Gaussian Surface:
We will take a spherical Gaussian surface of radius r (where b>r>c). The area of this surface is:
A=4πr2
4. Calculate the Enclosed Charge Qenc:
The charge enclosed by the Gaussian surface includes the charge from the inner sphere (radius c) and excludes the charge from the outer sphere (radius b):
- Charge from sphere with radius c:
Qc=σ⋅4πc2
- Charge from sphere with radius b:
Qb=−σ⋅4πb2
Thus, the total enclosed charge is:
Qenc=Qc+Qb=4πc2σ−4πb2σ=4πσ(c2−b2)
5. Substitute into Gauss's Law:
Now substituting Qenc into Gauss's Law:
E⋅4πr2=4πσ(c2−b2)ϵ0
6. Solve for Electric Field E:
Dividing both sides by 4πr2:
E=σ(c2−b2)ϵ0r2
Final Answer:
The magnitude of the electric field at a distance r from the center, where b>r>c, is given by:
E=σ(c2−b2)ϵ0r2
We have three concentric spheres:
- Sphere 1 (radius c): surface charge density σ
- Sphere 2 (radius b): surface charge density −σ
- Sphere 3 (radius a): surface charge density σ
According to Gauss's Law, the electric field E through a closed surface is proportional to the charge enclosed by that surface:
ΦE=∮E⋅dA=Qencϵ0
Here, dA is the differential area element on the Gaussian surface, and Qenc is the total charge enclosed by the Gaussian surface.
We will take a spherical Gaussian surface of radius r (where b>r>c). The area of this surface is:
A=4πr2
The charge enclosed by the Gaussian surface includes the charge from the inner sphere (radius c) and excludes the charge from the outer sphere (radius b):
- Charge from sphere with radius c:
Qc=σ⋅4πc2
- Charge from sphere with radius b:
Qb=−σ⋅4πb2
Thus, the total enclosed charge is:
Qenc=Qc+Qb=4πc2σ−4πb2σ=4πσ(c2−b2)
Now substituting Qenc into Gauss's Law:
E⋅4πr2=4πσ(c2−b2)ϵ0
Dividing both sides by 4πr2:
E=σ(c2−b2)ϵ0r2
The magnitude of the electric field at a distance r from the center, where b>r>c, is given by:
E=σ(c2−b2)ϵ0r2
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective type
Explore 7 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 15 Videos
Similar Questions
Three concentric spherical metallic spheres A,B and C of radii a,b and c(a<b<c) have surface charge densities σ,−σ and σ respectively.
View SolutionThree concentric metallic spherical shells A,B and C of radii a,b and c(a<b<c) have surface charge densities +σ,−σand +σ respectively ,the potential of shell B is
View Solution
Knowledge Check
Three concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−sigam and σ respectively. If VA,VB and VC denote the potentials of the three shells, then for c=a+b, we have
AVC=VB=VABVC=VA≠VBCVC=VB≠VADVC≠VB≠VA
A long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View SolutionThree concentric metallic spherical shell A,B and C or radii a,b and c(a<b<c) have surface charge densities −σ,+σand−σ. Respectively. The potential of shel A is :
View SolutionThree concentric spherical metal shells A.B.C of radii a,b,c(c>b>a) have surface charge density +σ,−σand+σ respectively. The potential of the middle shell is σε0 times
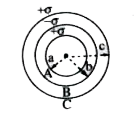
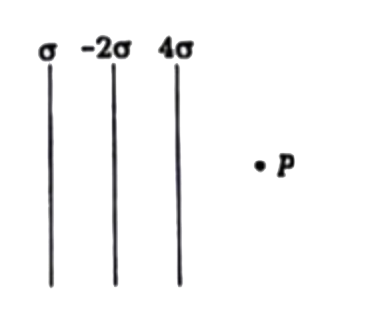
View SolutionThree non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
View SolutionThree concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−σ and σ respectively. If VA,VB and VC denote the potentials of the three shells, then for c=q+b, we have
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionThree concentric spherical metallic shells A,B and C of radii a,b and c (a<b<c) have surface charge densities σ,−σandσ respectively.
If the potential of shell B is VB=σ∈0(anb−b+c) and the potential of shell C is VC=σ∈0(anc−bnc+c) then n is .
View Solution
