Complete Solutions to Exercise 3.2 of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| CENGAGE PHYSICS | Exercise 3.2 |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
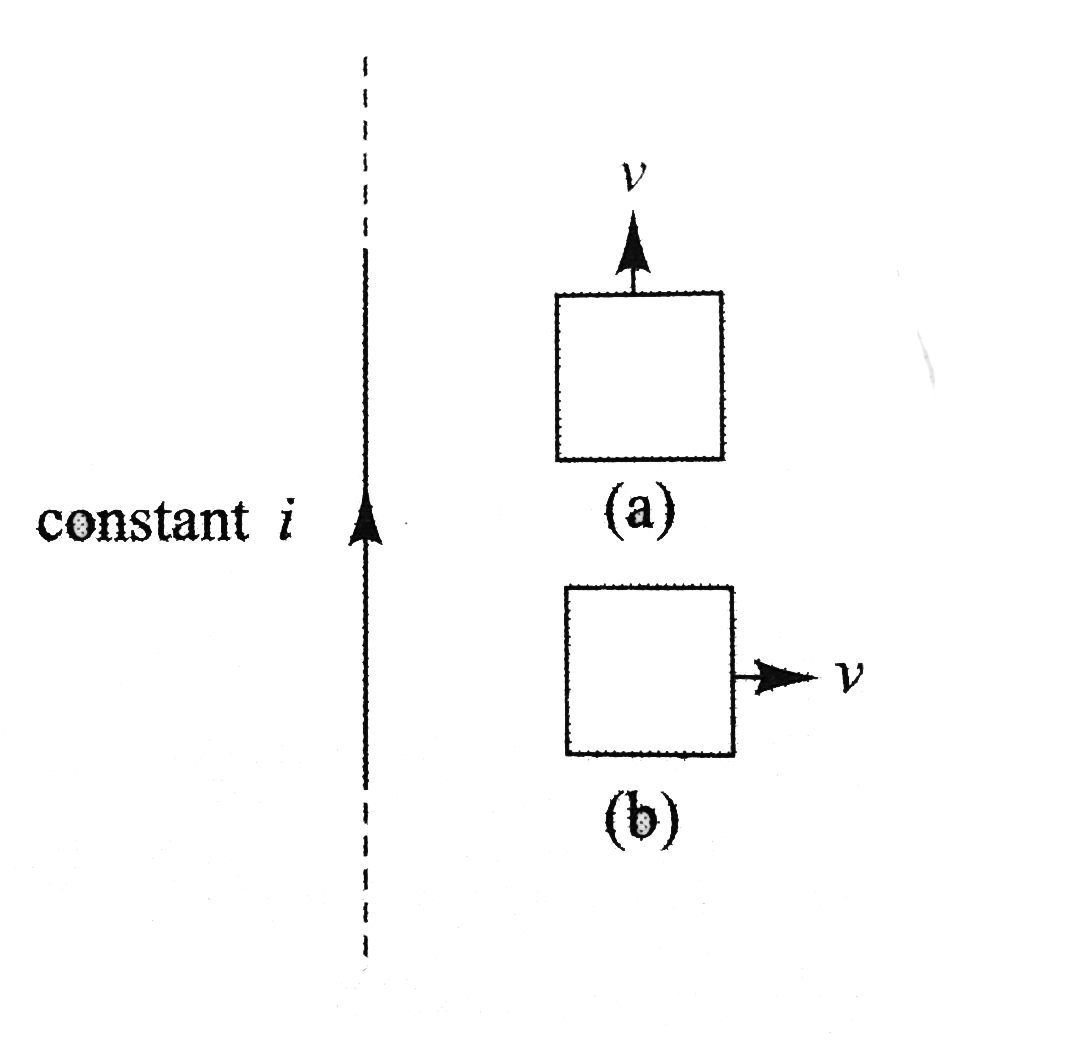
Shows a long current carrying wire and two rectangular loops moving with of velocity `v`. Find the direction of current in each loop.
View SolutionA rod of length `l` is moving velocity `v` "in magnetic field" `b` as seen in . Find the emf induced in all three cases.
(a)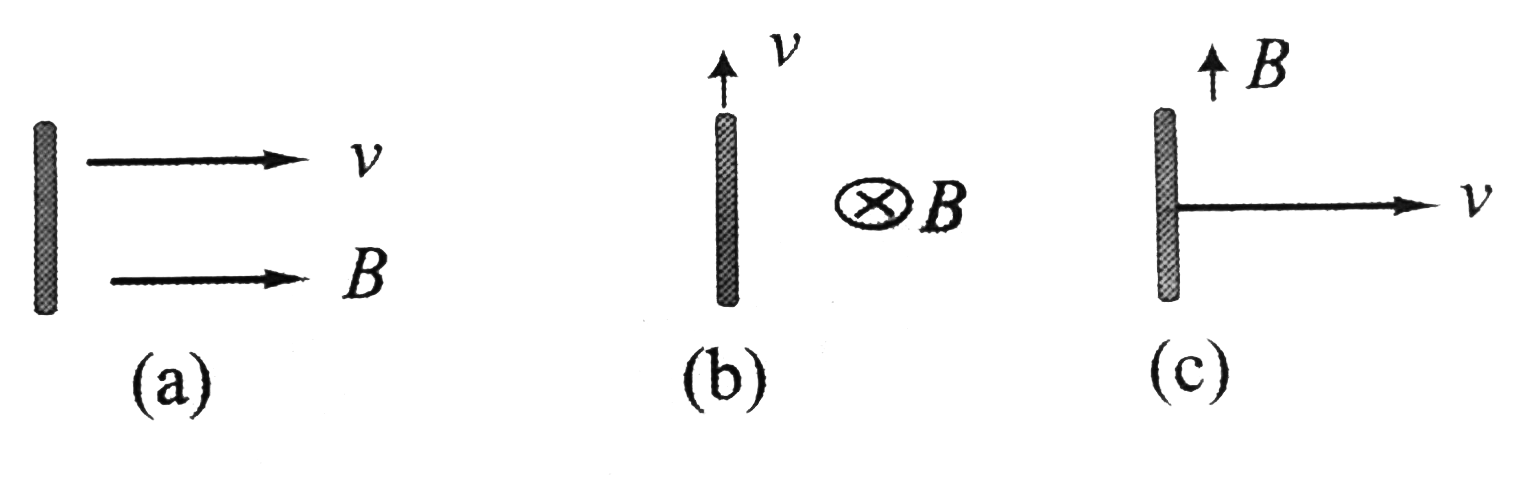
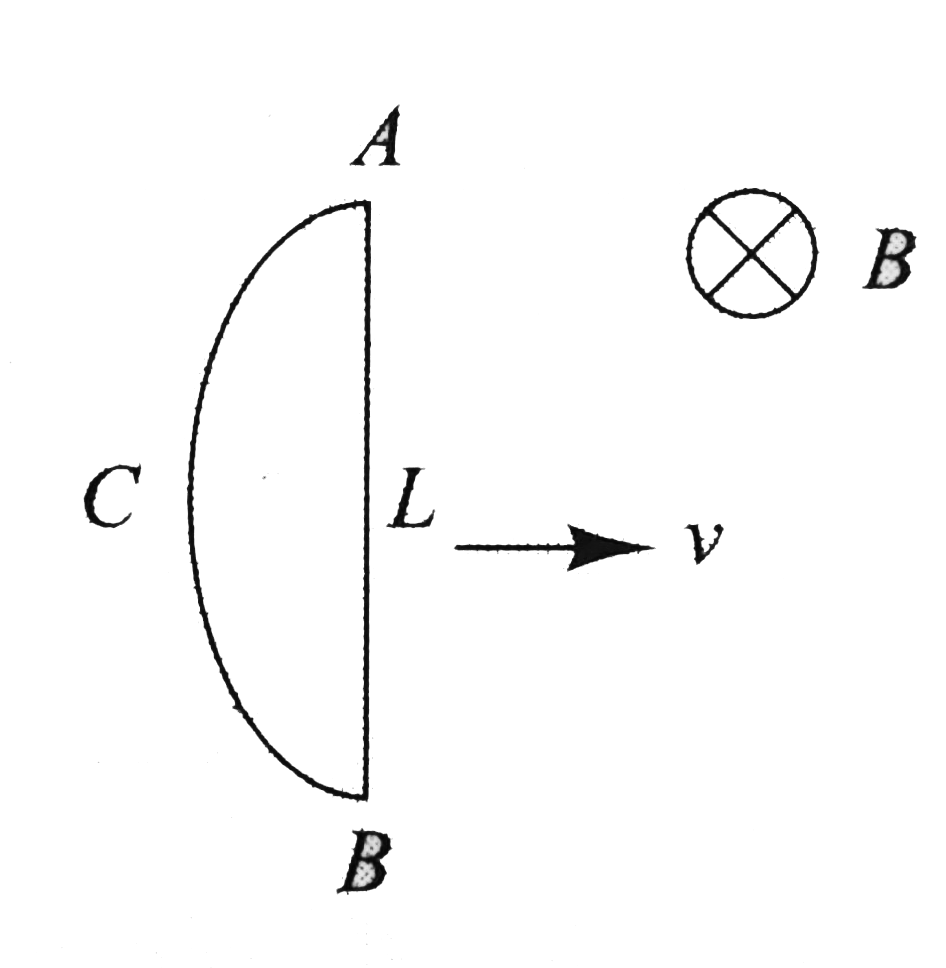
View SolutionShows a closed coil `ABCL` moving in a uniform magnetic field `B` with a velocity `v`.
Find
(a) emf induced in the coil.
(b) emf induced in curve part `ACB` and straight `AB` as `vev(L) xx vec(B)`
View SolutionShows an irregular shaped wire `AB` moving with velocity `v`. Find the emf induced in the wire.

View SolutionFind the emf across points `P` and `Q` which are diametrically opposite points of a semicircular closed loop moving in a magnetic field as shown in .

View SolutionFind the emf across points `P` and `Q` which are diametrically opposite points a semicircular closed loop moving in a magnetic field as shown in . Also draw the electrical equivalence od each branch.

View SolutionShows a rectangular loop moving in a uniform magnetic equivalence of each branch. What is the net induced emf.

View SolutionShows a rod of length `l` and resistance `r` moving on two rails shorted by a resistance `R`. A uniform magnetic field `B` is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
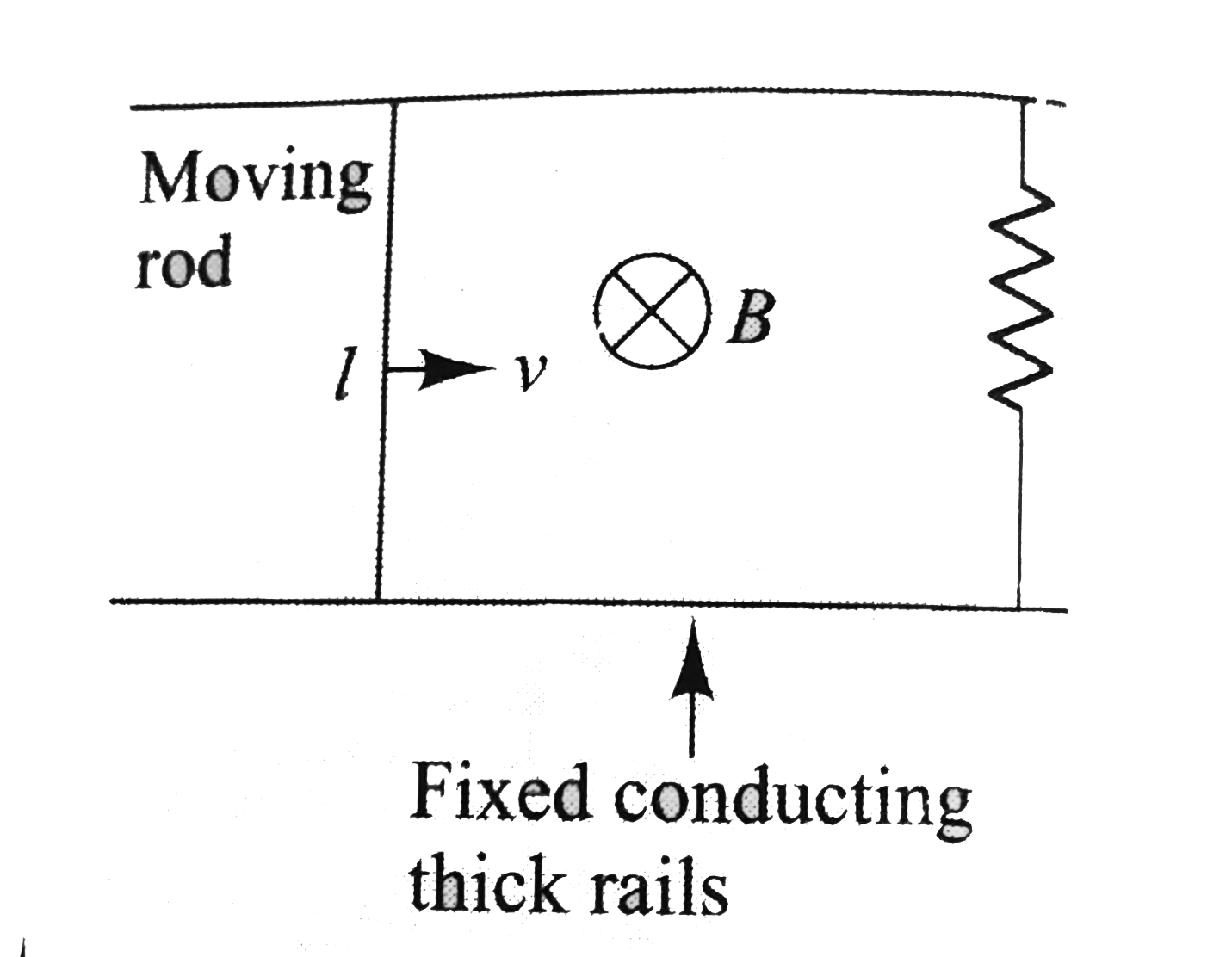
View SolutionA rod of length `l` is kept parallel to a long wire carrying constant current `i` . It is moving away from the wire with a velocity `v. Find the emf induced in the wire when its distance in the wire when its distance from the long wire is `x`.
View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current `I. Find the emf induced in the rectangualr loop.

View SolutionA rod of length `l` is placed perpendicular to a long wire carrying current `i`. The rod is moved parallel to the wire with a velocity `v`. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA rectangular loop is moving parallel to a long wire carrying current `i` with a velocity `v`. Find the emf induced in the loop (Fig. 3.68) if its nearest end is at a distance a from the wire. Draw equivalent electrical diagram.

View SolutionRod `PQ` of length `2l` is rotating about one end `P` in a uniform magnetic field `B` which is perpendicular to the plane of rotation of the rod . Point `M` is the mid- point of the rod. Find the induced emf between `M` and `Q` if the potential between `P` and `Q` is `100 V`.

View SolutionRod `PQ` of length `2l` is rotating about its midpoint `C` in a uniform magnetic field `B` which is perpendicular to the plane of rotation of the rod . Find the induced emf between `PQ` and `PC`. Draw the circuit diagram of parts `PC` and `CQ`.

View SolutionA rod of length `L` and resistance `r` rotates about one end as shown in . Its other end touches a conducting ring of negligible resistence. A resistence `R` is connected between the center and periphery. Draw the electrical equivalence and find the current in resistance `R`. There is a uniform magnetic field `B` directed as shown in .
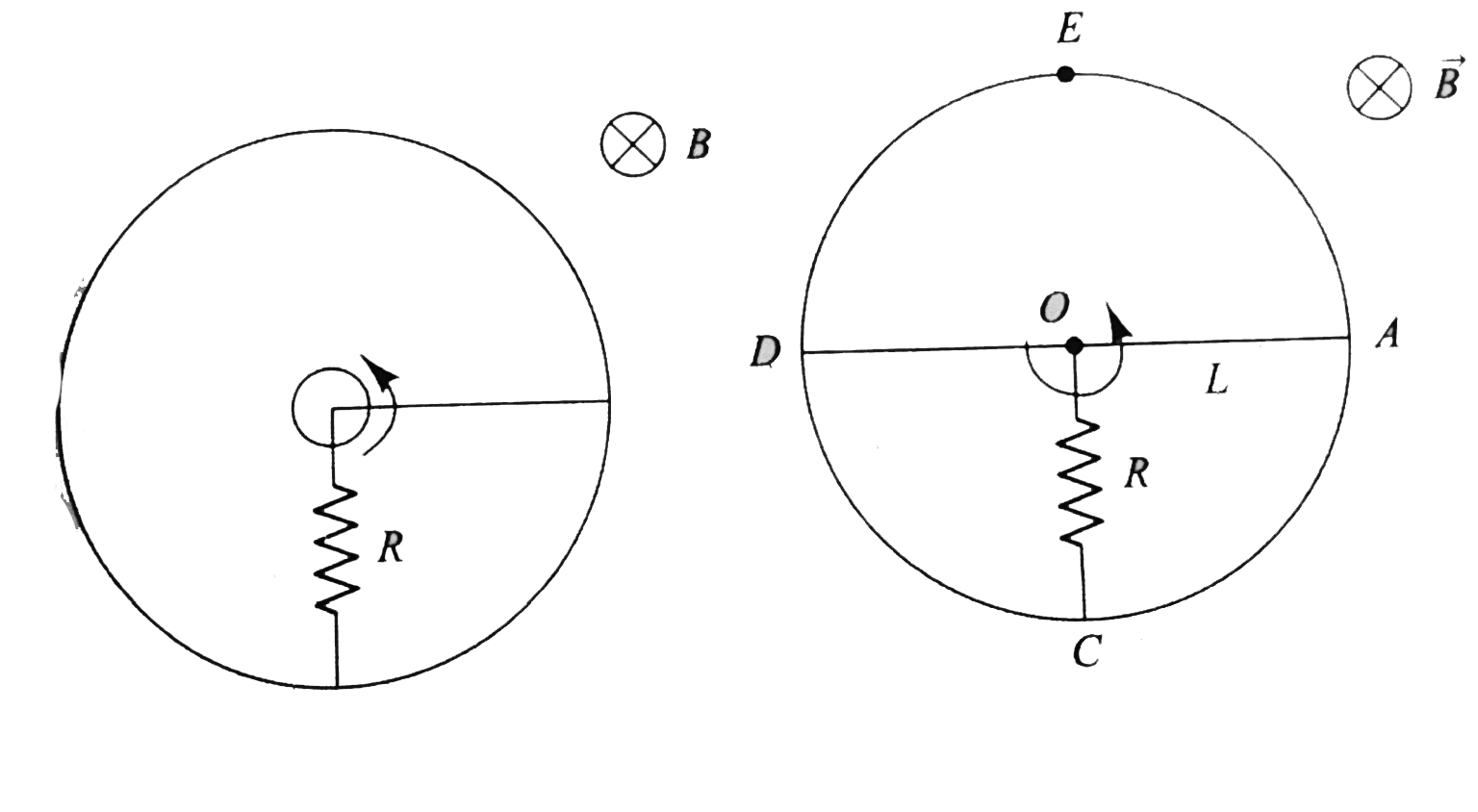
View SolutionSolve problem `15` if the length of rod is `2L` and resistance `2r` and it is rotating about its center. Both ends of the rod now touch the conducting ring.
View SolutionA rod of length `l` is rotating with an angular speed `omega` about one of its ends which is at a distance a from an infinitely long wire carrying current `i`. Find the emf induecd in the rod at the instanr shown in .
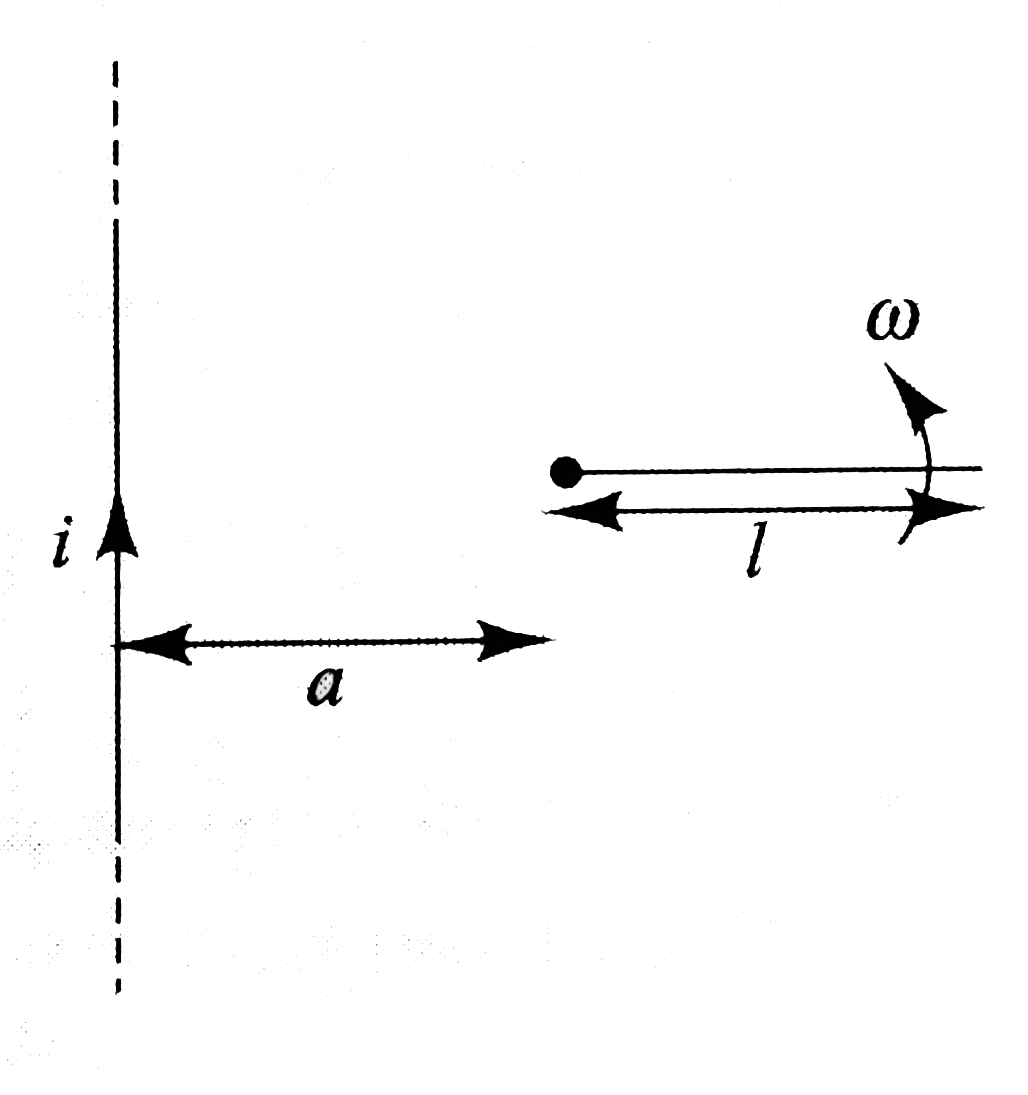
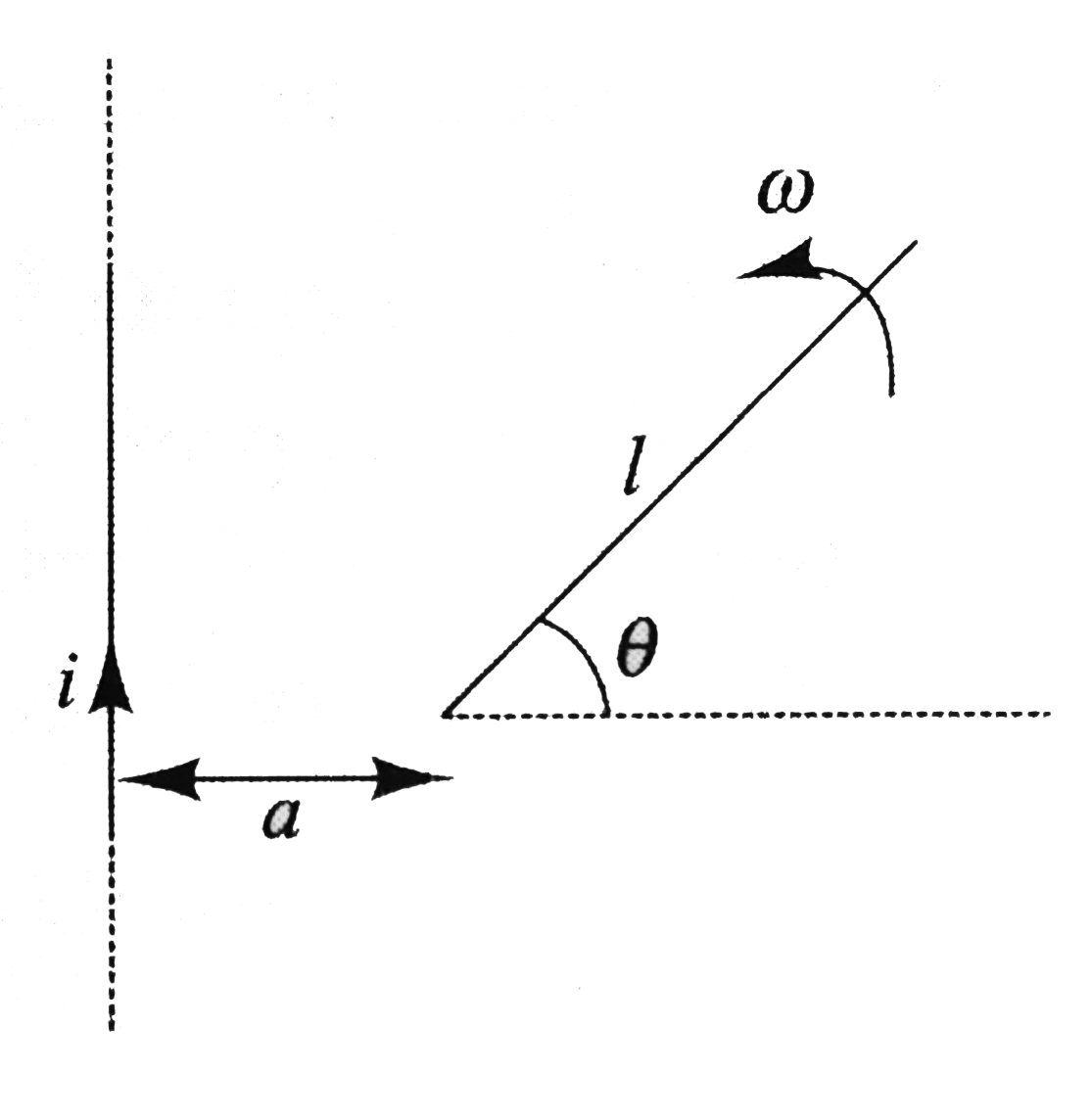
View SolutionA rod of length `l` is rotating with an angular speed `omega` about one of its ends which is at a distance a from an infinitely lonf wire carrying current `i`. Find the emf induced in the rod at the instant shown in .
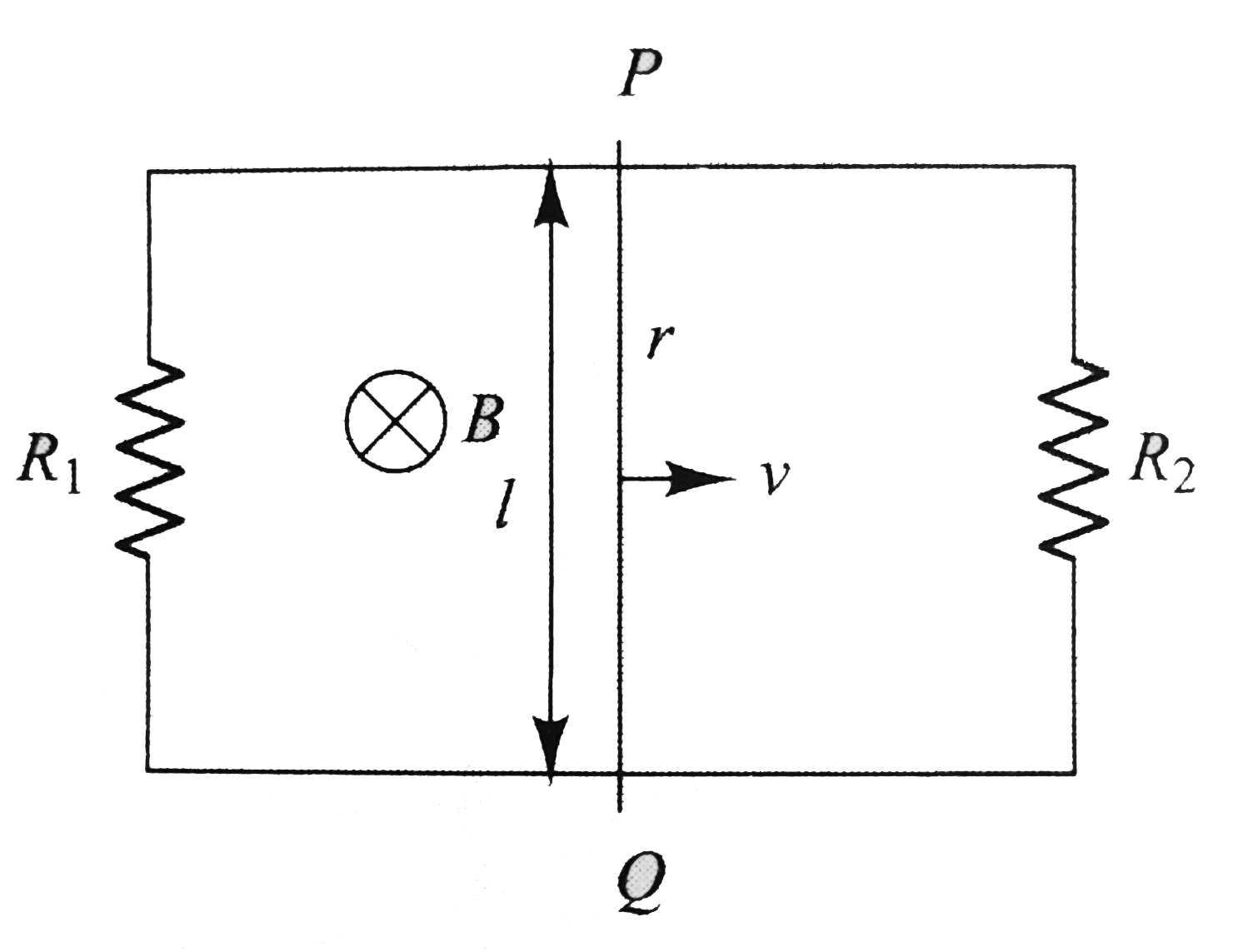
View SolutionShows rod `PQ` of mass `m` and resistance `r` moving on two fixed, resistanceless, smooth conducting rails (closed on both sides by resistances `R_(1) and R_(2)`). Find the current in the rod (at the instant its velocity is `v`).
View SolutionA rod `PQ` of length `l` is rotating about end `P`, with an angular velocity `omega`. Due to electrifugal forceed the free electrons in the rod move toward the end `Q` and an emf is created. Find the induced emf.

View SolutionA ring rotates with angular velocity `omega` about an axis perpendicula to the plane of the ring passing through the center of the ring (Fig. 3.77). A constant magnetic field `B` exists parallel to the axis. Find the emf induced in the ring.

View SolutionA ring rotates with angular velocity `omega` about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field `B` exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.

View Solutiona conducting rod of length `L = 30.0 cm` movies in a magnetic field `vec(B)` of magnitude `0.450 T` directed into the plane of the figure. The rod moves with speed `v = 5.00 m s^(-1)` in the direction shown.
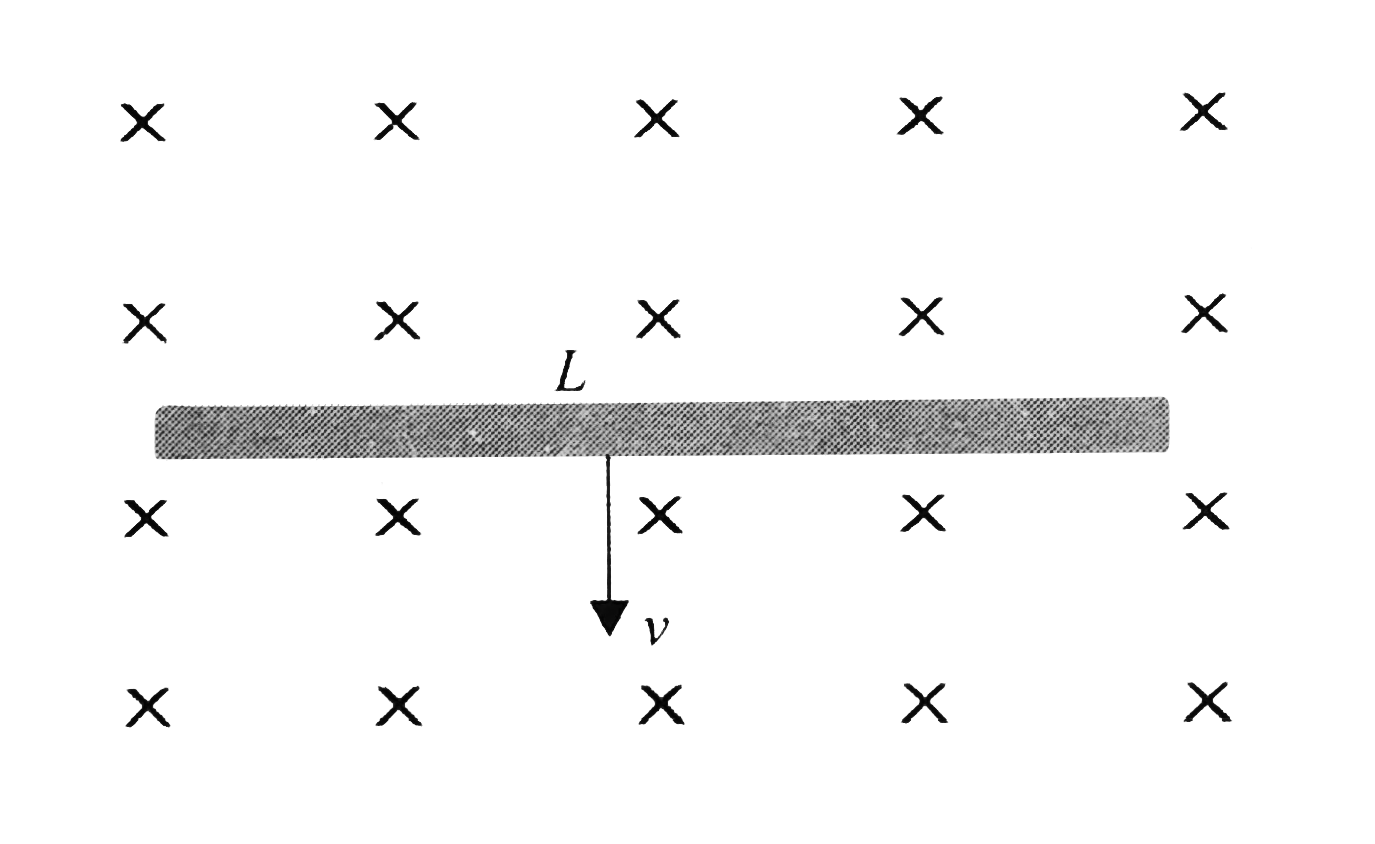
(a) What is motional emf inuced in the rod ?
(b) What is the potential difference between the ends of the rod?
( c) When point, `a or b`, is at higher potential?
(d) When the charges in the rod are in equilibrium, what are the magnitude and direction of the electric field within the rod?
(e) When the charges in the rod are in the rod in equilibrium, which point, `a or b`, has an excess of positive charge?
View SolutionThe cube shown in, `50.0 cm` on a side, is in a uniform magnetic field of `0.120 T`, directed along the positive y-axis. Wires `A, C, and D` move in the direction indicated, each with a speed of `0.350 ms^(-1)`. (Wire `A` moves parallel to the x-y plane, `C` moves at an angle of `45.0^(@)` below the x-y plane, and `D` moves parallel to the x-z plane.) What is the potential difference between the ends of each wire?

View SolutionA rod of mass `m`, length `l` and resistance `R` is sliding down on a smooth inclined parallel rails with a cinstant velocity `v`. If a uniform horizontal magnetic field `B` exists, then find thevalue of `B`.
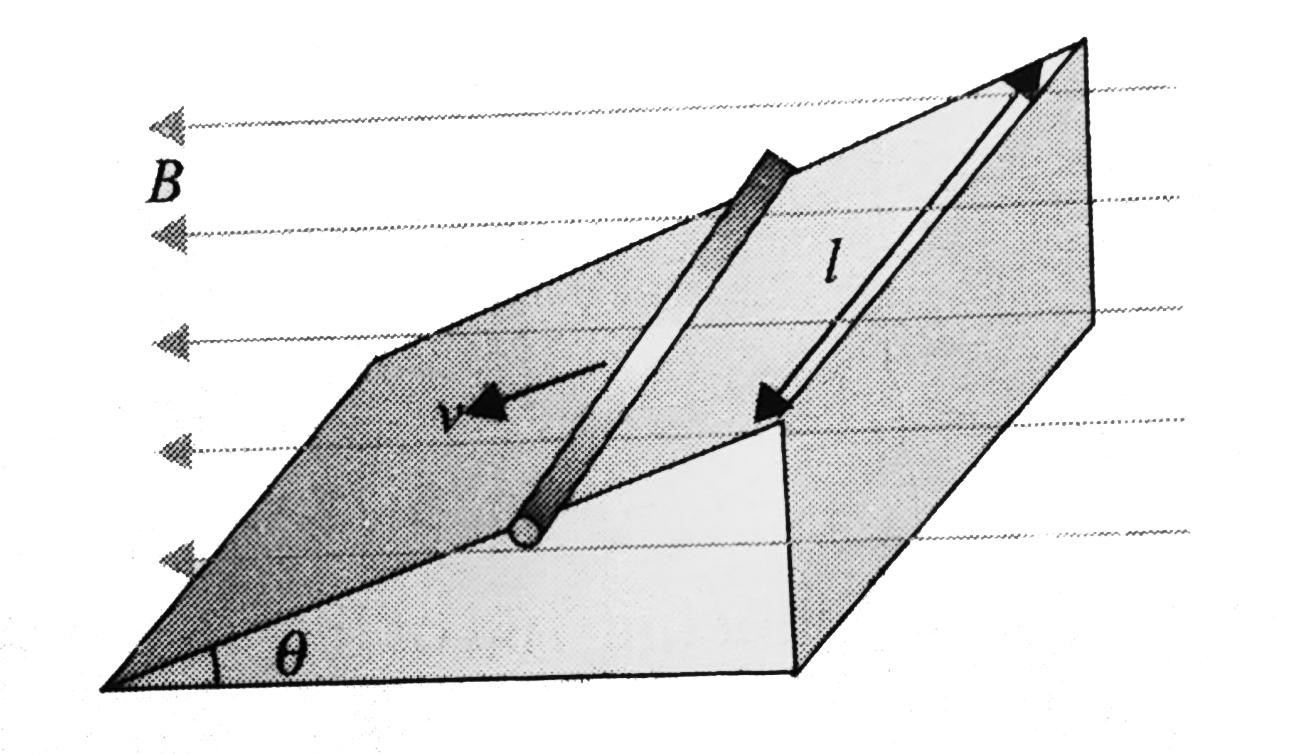
View SolutionA conducting rod `AC` of length `4l` is rotated about point `O` in a uniform magnetic field `vec(B)` directed into the plane of the paper. `AO = l and OC = 3l`. Find `V_(A) - V_(C)`.

View SolutionConsider the sliding wire circuit shown in . The wire slides at constant speed and the plane of the circuit is perpendicular to a uniform magnetic field. Show that the induced emf is given by `E = Blv^(2)t//D` foe `0 lt t lt D//v` What is the expression for the emf for `t gt D//v`?
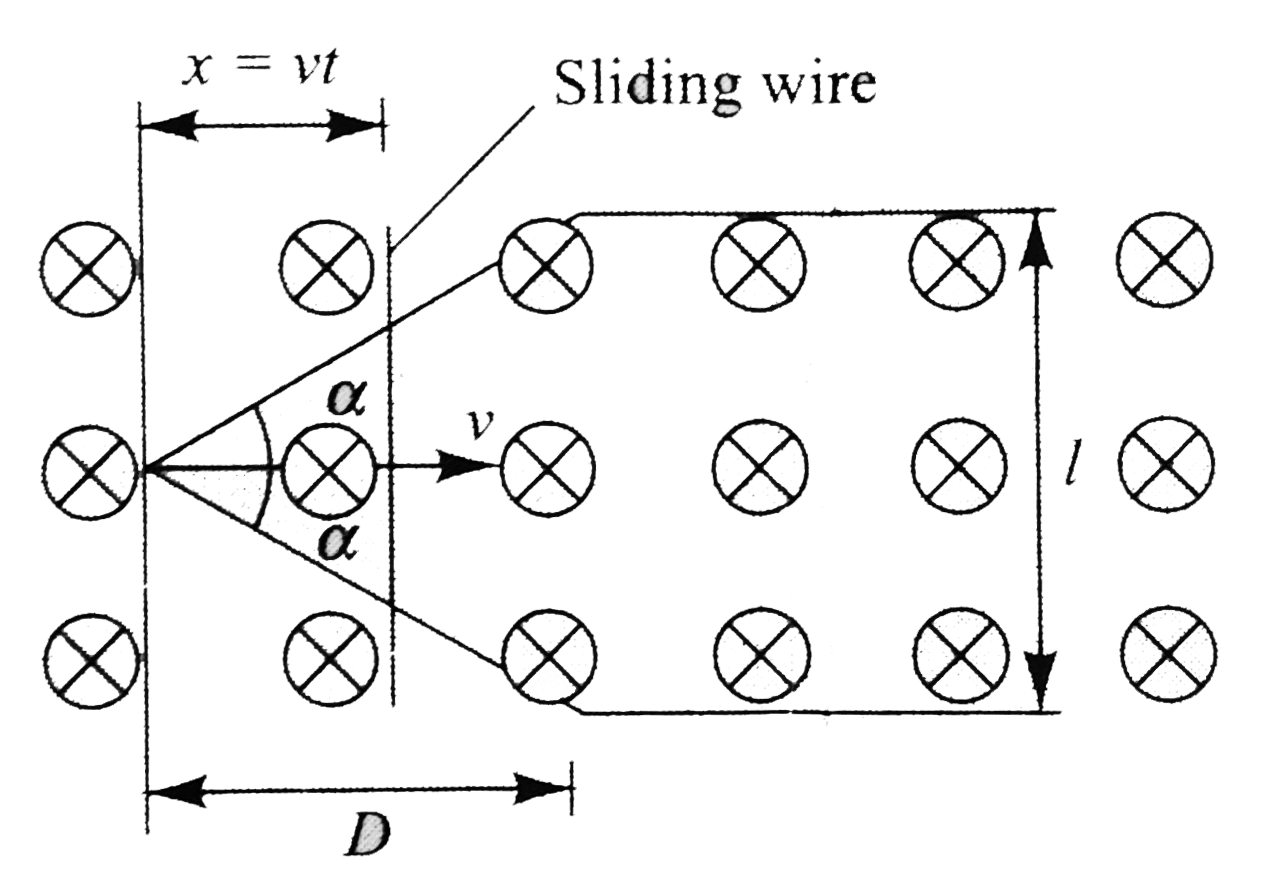
View Solution
Exercise 3.2 questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of CENGAGE PHYSICS (HINGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS ELECTROMAGNETIC INDUCTION
- Archives Asserton - Reasoning
- Archives Fill In The Blanks
- Archives Multiple Correct
- Archives Single Correct
- comprehensive
- comprehensive type
- compression type
- Exercise 3.1
- Exercise 3.2
- Exercises Asserton - Reasoning
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises Subjective
- Illustration
- Multiple correct Answer Type
- single correct
- single correct
- single correct answer
- Single Correct Answer Type
- Solved Example