Complete Solutions to Interger Answer type of chapter MISCELLANEOUS VOLUME 3 of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MISCELLANEOUS VOLUME 3 |
| CENGAGE PHYSICS | Interger Answer type |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
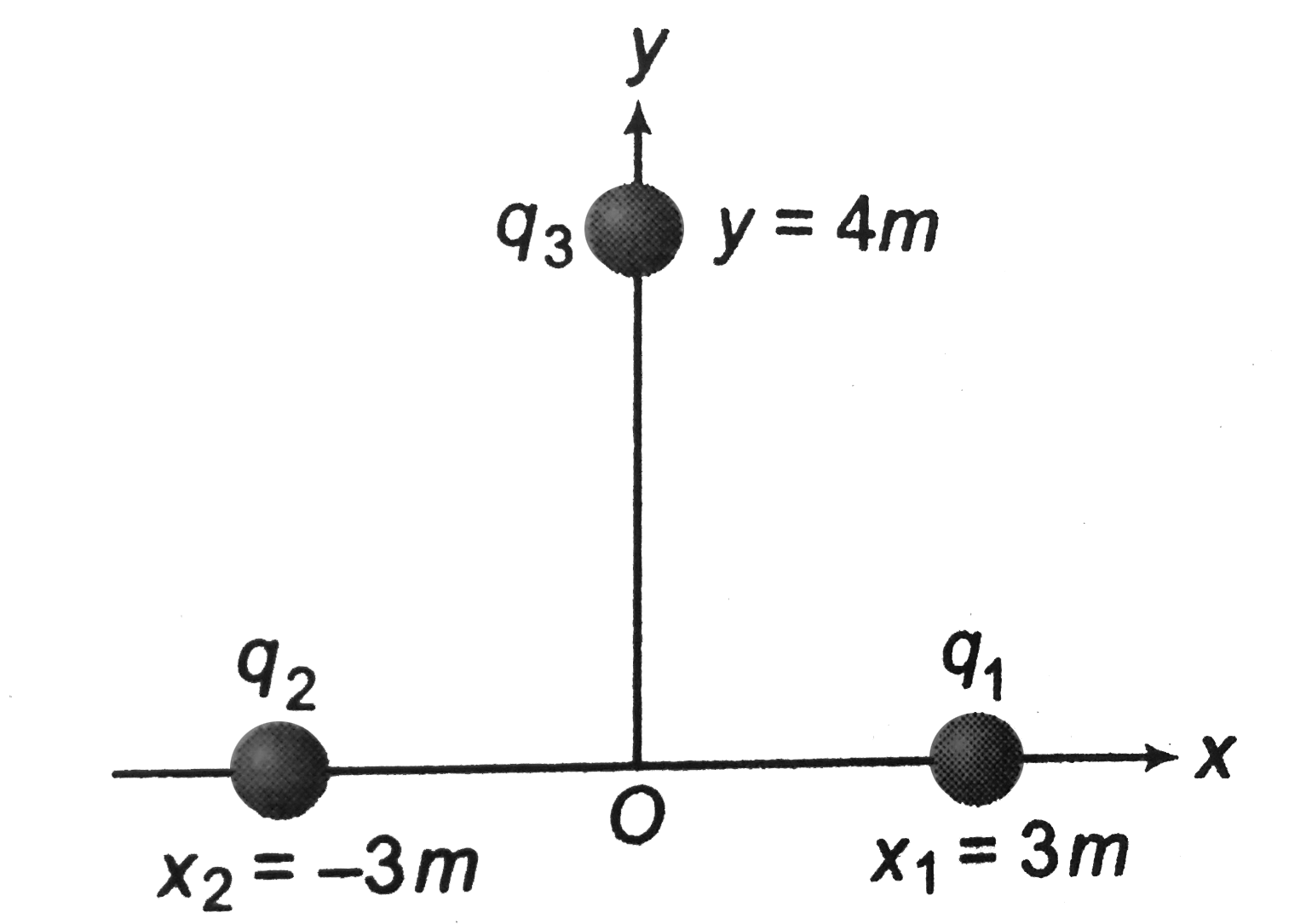
Two point charges `q_1=q_2=2muC` are fixed at `x_1=+3 m` and `x_2=-3m` as shown in figure. A third particle of mass 1 g and charge `q_3=-4muC` are released from rest at `y=4.0m`.Find the speed of the particle as it reaches the origin.
View SolutionTwo concentric spherical conducting shells of radii `R` and `2R` carry charges `Q` and `2Q`respectively.Change in electric potential on the outer shell when both are connected by a conducting wire is `(k=(1)/(4 pi varepsilon_(0)))`
View SolutionThe capacitance of a capacitor between` 4//3` times its original value if a dielectric slab of thickness `t=d//2` is inserted between the plates (d is the separation between the plates). What is the dielectric consant of the slab?
View SolutionA particle having charge that of an electron and mass `1.6xx10^(-30)`kg is projected with an initial speed u at the angle `45^(@)` to the horizontal from the lower plate of a parallel-plate capacitor as shown in fig. The plates are sufficiently long and have a separation of 2 cm, find the maximum value of the velocity of he particle so that it does not hit the upper plate. Take the electric field between the plates as `10^(3)Vm^(-1)` directed upward.

View SolutionThe electric field in a region is radially outward with magnitude `E = ar`. If `a = 100 Vm^(-2)` and `R = 0.30m`, then the value of charge contained in a sphere of radius R centred at the origin is `W xx 10^(-10)C`. Find W.
View SolutionA wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
View SolutionA Uniform electric field of `10NC ^(-1)` exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50cm.
View SolutionThe kinetc energy of a chargd particle decreased by 10 J as it moves from a point at potential 100 V to a point at potential 200V . Find the charge on the particle.
View SolutionA charge of 20 `muC` is placed on the positive plante of on isolated parailel - plate capacitor of capacitance `10 muF` calculate the potential difference developed between the plates .
View SolutionA capacitor with stored energy `4.0J` is connected with an identical capacitor with no electric fileld in between . Find the total energy stored in the two capactors .
View SolutionExcess electrons are placed on a small lead sphere of mass `6.90 ` g so that its net charge is `-3.20 xx 10^(-9)C`. Find the number of excess electorns ( in terms of `xx 10^(10))` on the sphere.
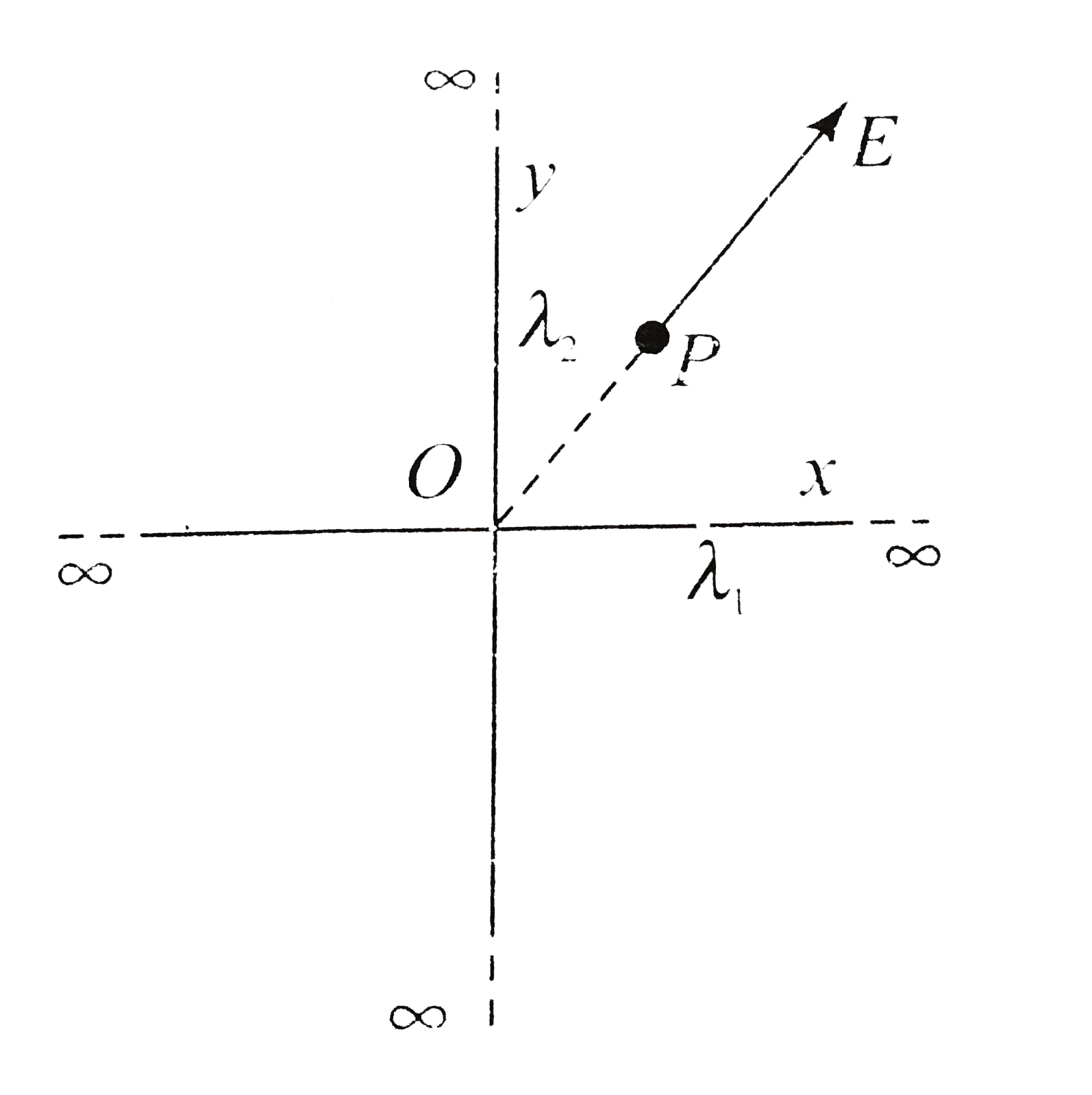
View SolutionTwo mutually perpendicular infinite wires along x-axis and y-axis carry charge densities `lambda_1 and lambda_2`. The electric line of force at P is along the line `y = x//(sqrt3)`, where P is also a point lying on the same line. Find `lambda_2//lambda_1`.
View SolutionThe electric field strength depends only on the x, y, and z coordinates according to the law `E = (a(xhati+yhatj+zhatk))/(x^2+y^2+z^2)^3//2`, where ` a = 280 Nm^2C^(-1)` is a constant. If the potential difference between (3,2,6) and (0,3,4) is `x^2`. What is the value of x.
View SolutionA positive charge `+q_1` is located to the left of a negative charge `-q_2`. On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity.The first place is between the charge and is 4.00 cm to the left of the negative charge. The second place is 7.00 cm to the right of the negative charge. If `q_2 = -12muC and q_1 = 11 xx xmuC`, what is the value of x.
View SolutionFigure shows, in cross section , two solid spheres with uniformly distributed charge throughout their volumes. Each has radius R. Point O lies on a line connecting the centers of the spheres, at radial distance `R//2` from the center of sphere 1. If the net electric field at point P is zero, and `Q_1 is 64muC` and `Q_2 = 8xmuC`, what is the value of x.
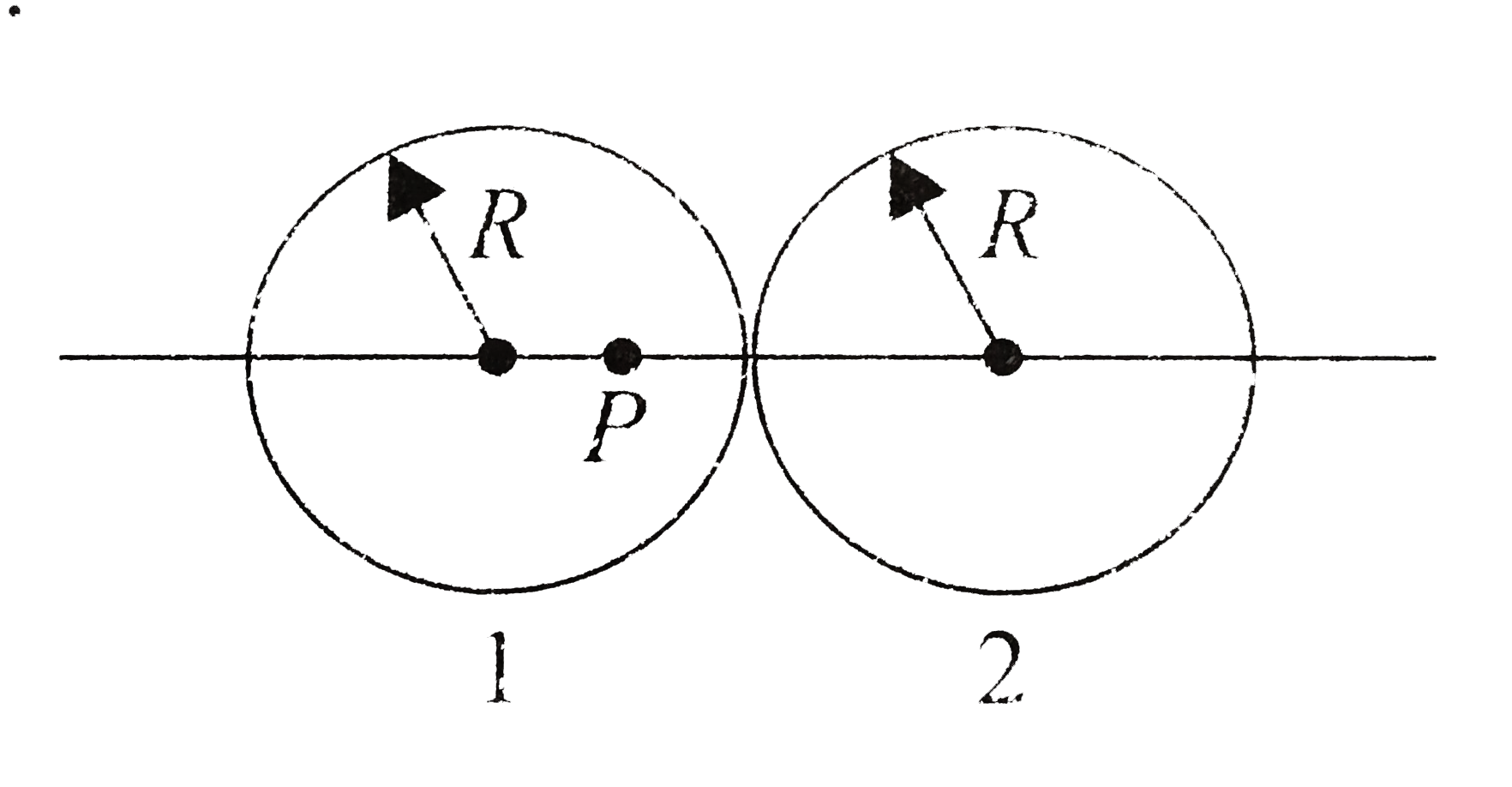
View SolutionA positively charged particle starts at rest 25 cm from a second positively charged particle, which is held stationary throughout the experiment. The first particle is released and accelerates directly away from the second particle. When the first particle has moved 25 cm, it has reached a velocity of `10(sqrt2)ms^(-1)` . What is the maximum velocity `(in xx 10 ms^(-1))` that the first particle will reach?
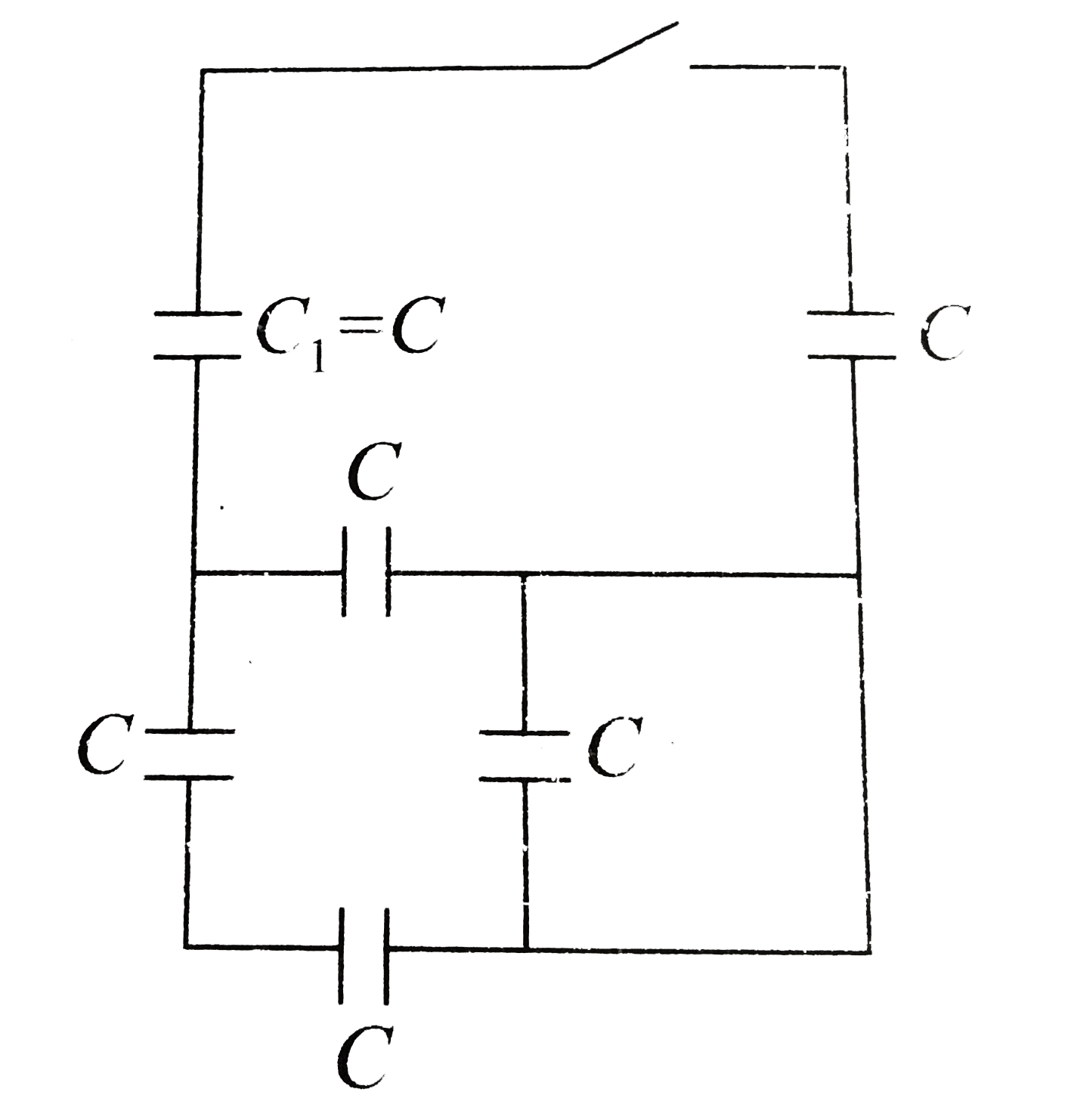
View SolutionIn the circuit shown, all capacitors are identical. Initially, the switch is open and the capacitor marked `C_1` is the only one charged to a value `Q_0`. After the switch is closed and the equilibrium is reestablished, the charge on the capacitor marked `C_1` is Q. Find the ratio initial change to final charge in capacitor `C_1`.
View SolutionTwo small spheres are attached to the ends of a long light nonconducting rod at a distance 40 mm from each other. All three spheres are nonconducting, have identical masses `m = 1 g`, and a positive charge `q = 1C` is distributed evenly on the surface of each sphere. The whole system is placed on a horizontal frictionless nonconducting surface. Initially, all three spheres are at rest and the middle sphere is located a distance 30 mm from one of the ends of the rod and a distance 10 mm from the other. Find the maximum speed v `(in ms^(-1))` of the middle sphere after the system is released.
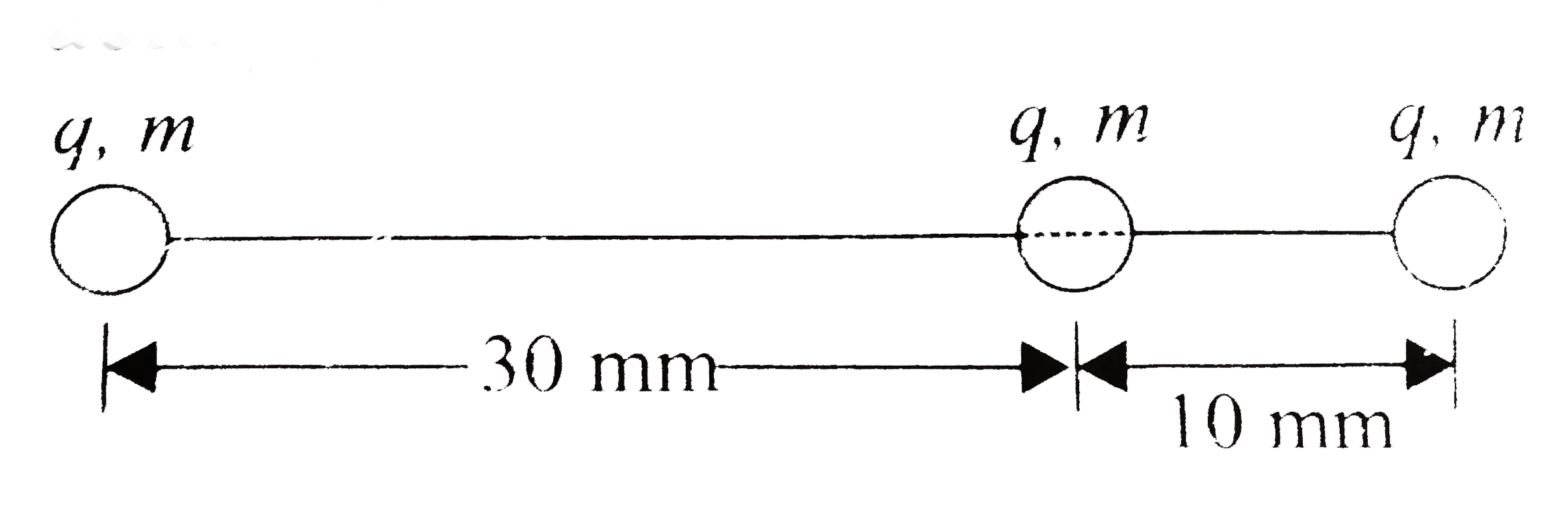
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density `rho=kr^a`, where k and a are constants and r is the distance from its centre. If the electric field at `r=(R)/(2)` is `1/8` times that `r=R`, find the value of a.
View SolutionAn infinitely long solid cylinder of radius ` R` has a uniform volume charge density `rho`. It has a spherical cavity of radius `R//2` with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point `P`, which is at a distance `2 R` form the axis of the cylinder, is given by the expression `( 23 r R)/( 16 k e_0)` . The value of `k` is .
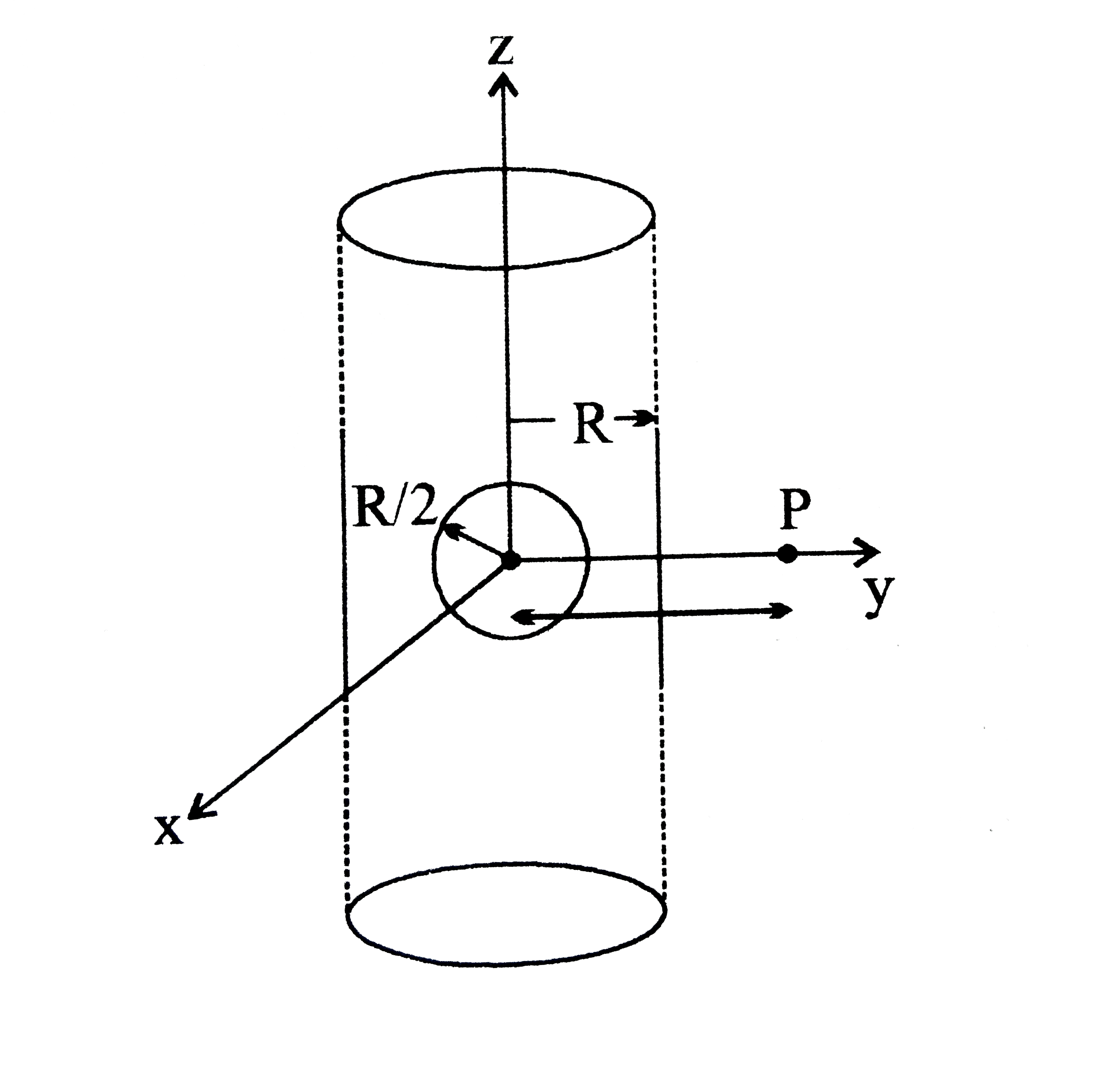 .
.
View Solution
Interger Answer type questions and complete solutions for chapter MISCELLANEOUS VOLUME 3 of CENGAGE PHYSICS (HINGLISH) of Class 12