Complete Solutions to Comprehension Type of chapter CENGAGE PHYSICS DPP of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CENGAGE PHYSICS DPP |
| CENGAGE PHYSICS | Comprehension Type |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
If a particle starts moving along a straight ine withinitial velocity u under contact acceleration a, its displacement with time is given by the relation `x=ut+(1)/(2)at^2`
Q. Differentiation of `x` w.r.t. `t` will be
View SolutionIf a particle starts moving along a straight ine withinitial velocity u under contact acceleration a, its displacement with time is given by the relation `x=ut+(1)/(2)at^2`
Q. The concerned deviation of positon time realtion w.r.t will be. Differentiation of above result w.r.t. `t` will be
View SolutionIf charge flown through a wire is given by `q=3sin(3t)`, then
Q. Find out the amount of charge flown through the wire at `t=((pi)/(6))` seconds.
View SolutionIf charge flown through a wire is given by `q=3sin(3t)`, then
Q. Find out the current flown through the wire at `t=(pi)/(9)` second.
View SolutionVelocity of a particle varies as `v=2t^3-3t^2` in `(km)/(hr)` If `t=0` is taken at 12:00 noon
Q. Find the expression for the acceleration of the particle.
View SolutionVelocity of a particle varies as `v=2t^3-3t^2` in `(km)/(hr)` If `t=0` is taken at 12:00 noon
Q. Find the time between 12:00 noon and 1:00 pm which speed is maximum
View SolutionVelocity of a particle varies as `v=2t^3-3t^2` in `(km)/(hr)` If `t=0` is taken at 12:00 noon
Q. The time at which speed of the particle is minimum.
View SolutionVelocity of a particle varies as `v=2t^3-3t^2` in `(km)/(hr)` If `t=0` is taken at 12:00 noon
Q. What is the velocity of the particle at 12:00 noon?
View SolutionIf `a=(3t^2+2t+1)` `m/s^2` is the expression according to which the acceleration of a particle varies. Then-
`a=(3t^2+2t+1)` `(m)/(s^2)`
Q. The expression for instantaneous velocity at any time `t` will be (if the particle was initially at rest)-
View SolutionIf `a=(3t^2+2t+1)` `m/s^2` is the expression according to which the acceleration of a particle varies. Then-
`a=(3t^2+2t+1)` `(m)/(s^2)`
Q. The change in velocity after 3 seconds of its start is:
View SolutionIf `a=(3t^2+2t+1)` `m/s^2` is the expression according to which the acceleration of a particle varies. Then-
`a=(3t^2+2t+1)` `(m)/(s^2)`
Q. Find displacement of the particle after 2 seconds of start.
View SolutionA man is standing on top of a building 100 m high. He throws two ball vertically, one at `t=0` and after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. At `t=2`, both the balls reach to their and second ball is `+15m`.
Q. The speed of first ball is
View SolutionA man is standing on top of a building 100 m high. He throws two ball vertically, one at `t=0` and after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. At `t=2`, both the balls reach to their and second ball is `+15m`.
Q. The time interval between the throw of ball is
View Solution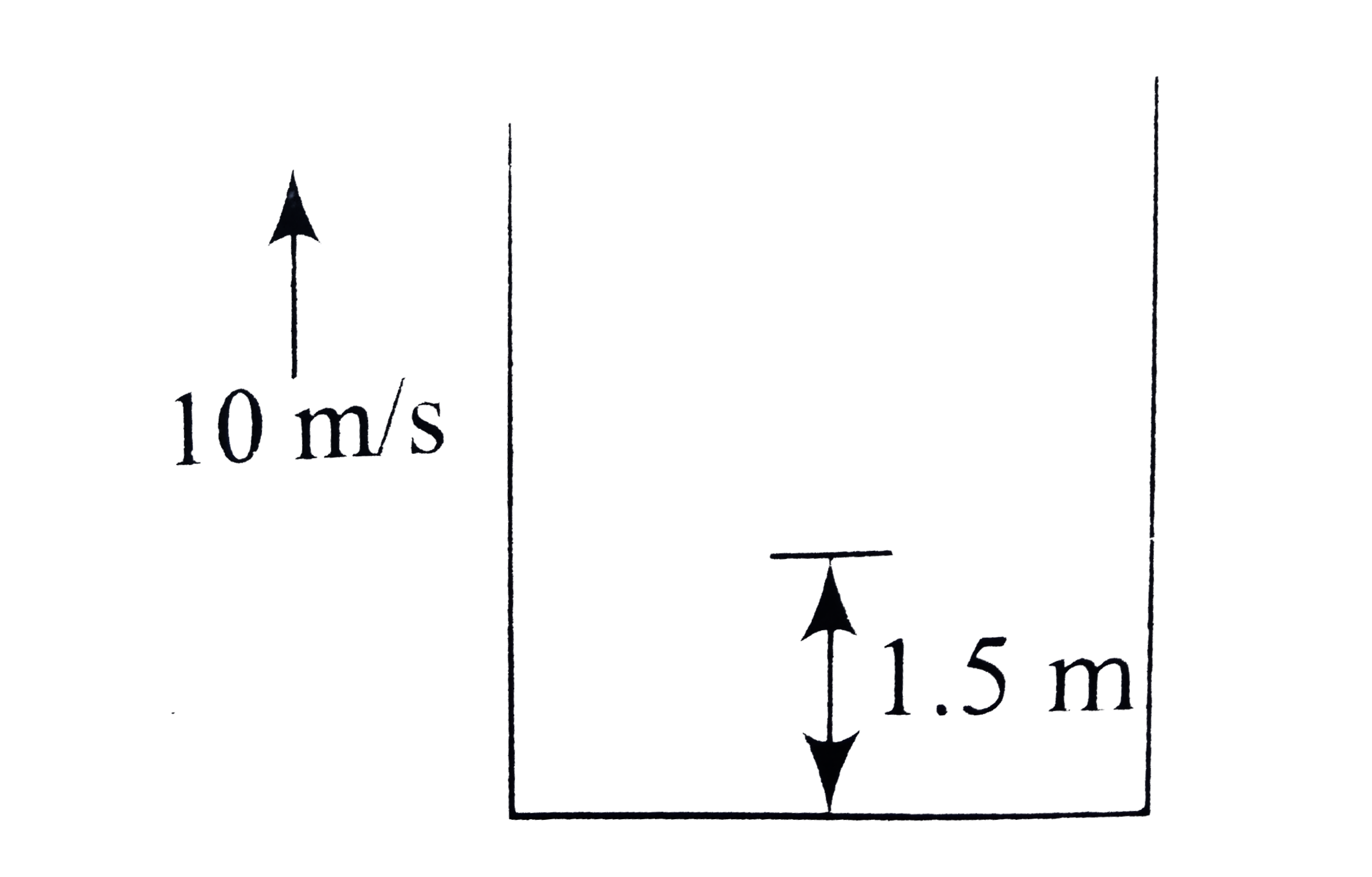
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the acceleration of the elevator in upward direction, `((ms)/(s^2))`:
View Solution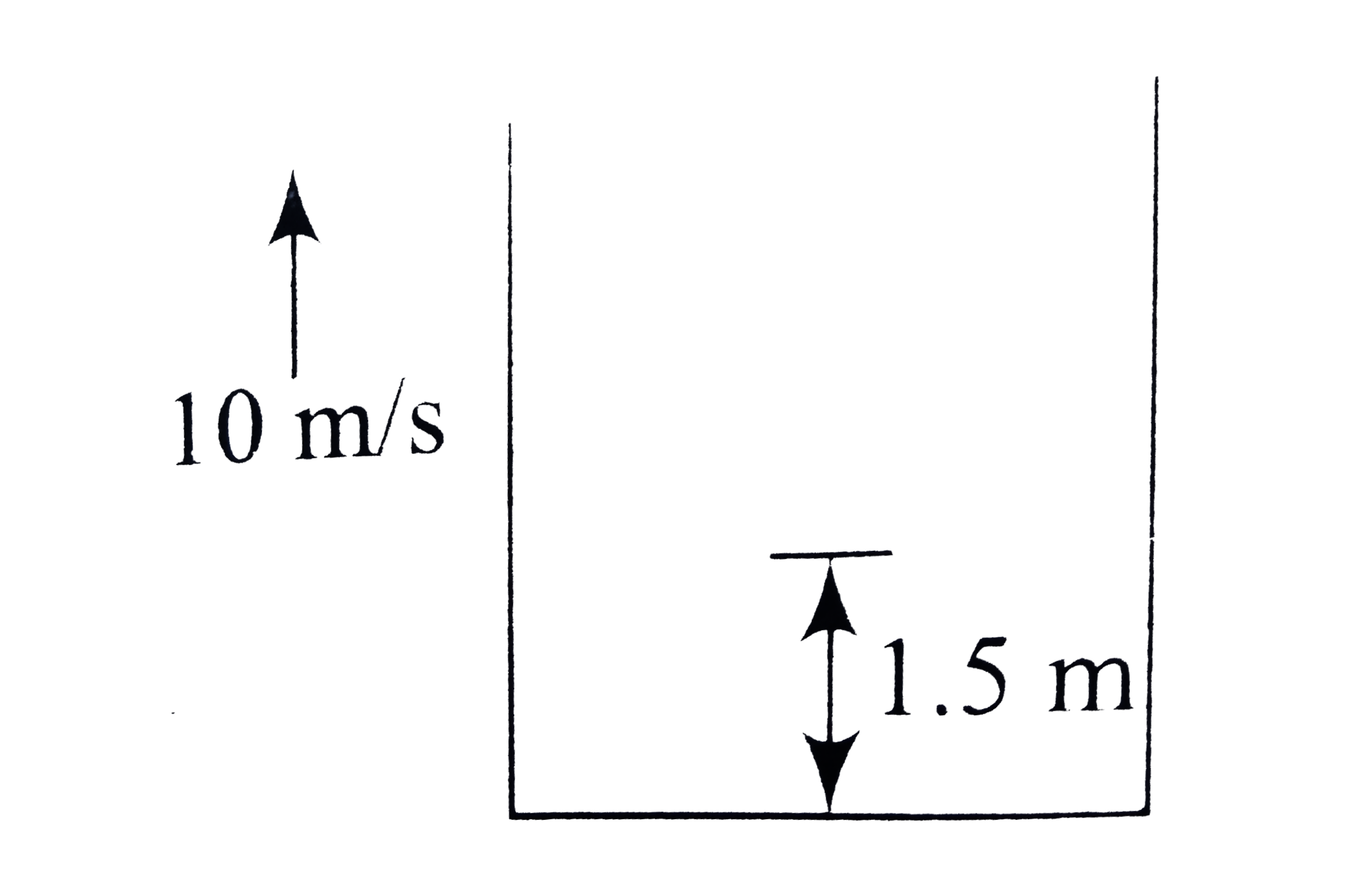
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the displacement of the bullet relative to ground during its flight:
View Solution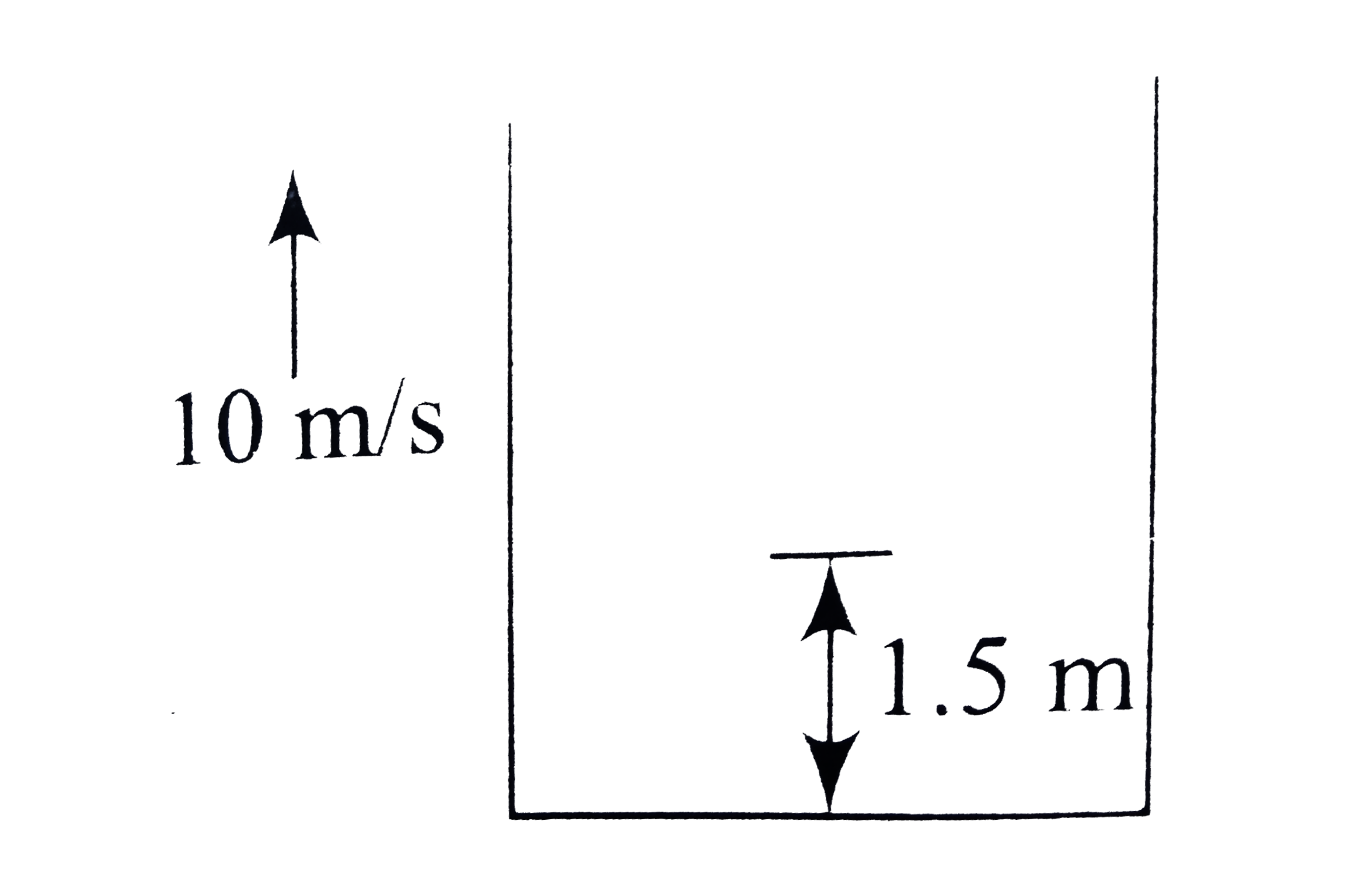
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :
View Solution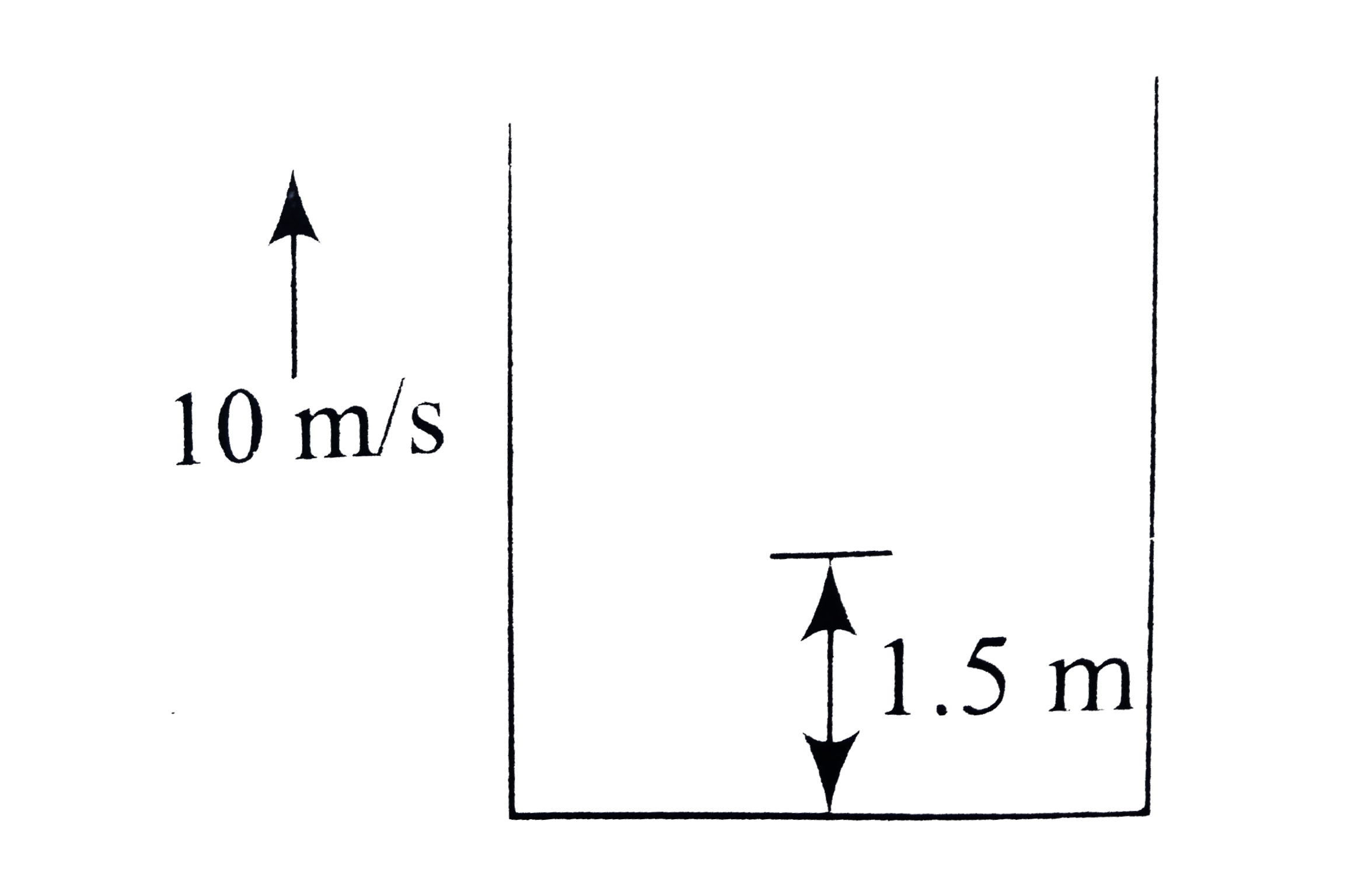
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the distance travelled by bullet during its flight:
View SolutionPoints `A` and `C` are on the horizontal ground and `A` and `B` are in same vertical plane at a distance of `1500 m`. Simultaneously bullets are fired from `A,Bll` and `C` and they collide at `O`. The bullets at `B` is fired at an angle of `30^(@)`with horizontal towards the ground iat velocity `100 m//s`. the bullet at `C` is projected vertically upwards at velocity of `100 m//s`. the bullet projected from `A` reaches its maximum height at `O`.
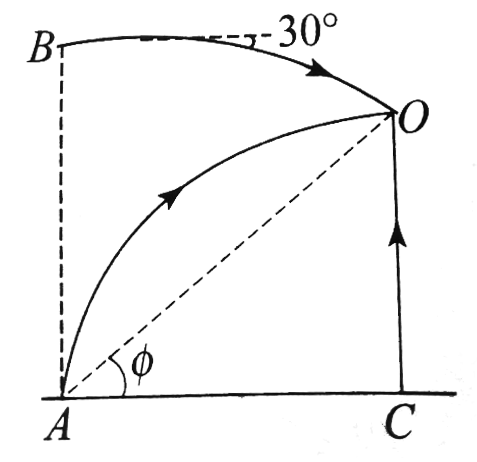
Find the time in which bullets will collide (seconds ):
View SolutionPoints `A` and `C` are on the horizontal ground and `A` and `B` are in same vertical plane at a distance of `1500 m`. Simultaneously bullets are fired from `A,Bll` and `C` and they collide at `O`. The bullets at `B` is fired at an angle of `30^(@)`with horizontal towards the ground iat velocity `100 m//s`. the bullet at `C` is projected vertically upwards at velocity of `100 m//s`. the bullet projected from `A` reaches its maximum height at `O`.
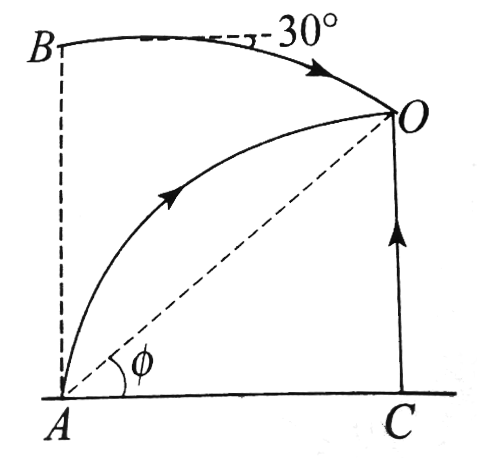
Find the elevation angle `angletheta=angleOAC`:
View SolutionPoints `A` and `C` are on the horizontal ground and `A` and `B` are in same vertical plane at a distance of `1500 m`. Simultaneously bullets are fired from `A,Bll` and `C` and they collide at `O`. The bullets at `B` is fired at an angle of `30^(@)`with horizontal towards the ground iat velocity `100 m//s`. the bullet at `C` is projected vertically upwards at velocity of `100 m//s`. the bullet projected from `A` reaches its maximum height at `O`.
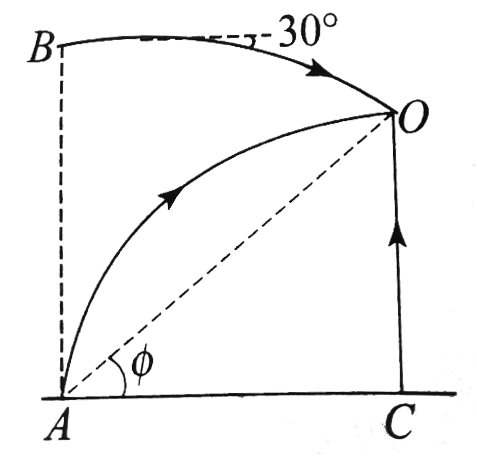
Find the velocity of bullet at `A`:
View Solution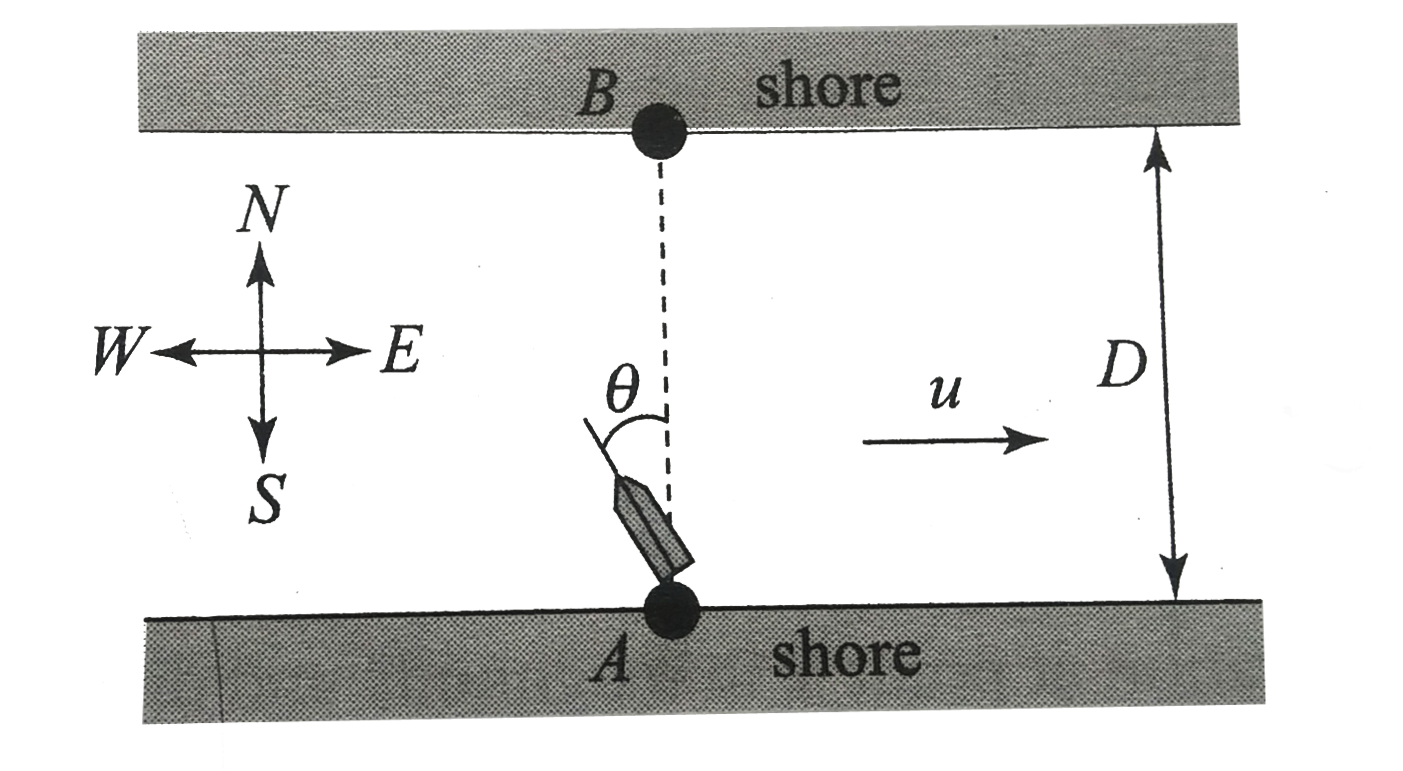
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume `v=2u`
Q. What is the direction of the velocity of boat relative to river `theta`, sothat it crosses directly on a line from A to B?
View Solution
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume `v=2u`
Q. Suppose the boat wants to cross the river from A to the other side in the shortest possible time. Then what should be the direction of the velocity of boat relative to river?
View Solution
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume `v=2u`
Q. The boat crosses the river from A to the other side in shortest possible time, then how far is the boat from the port B after crossing the river
View Solution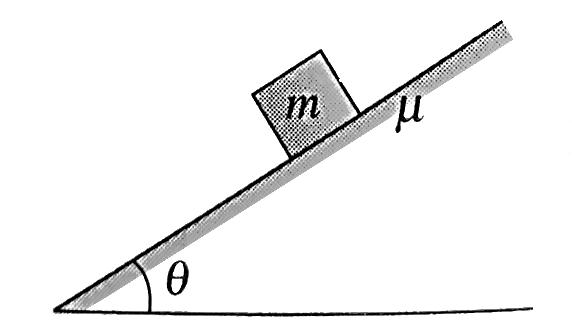 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If the entire system, were accelerated upward with acceleration `a` the angle of repose, would:
View Solution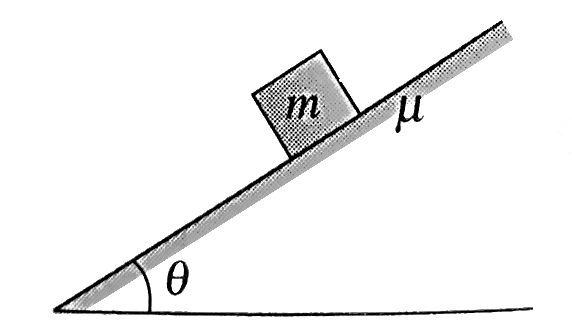 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. For what value of `theta` will the block slide on the inclined plane:
View Solution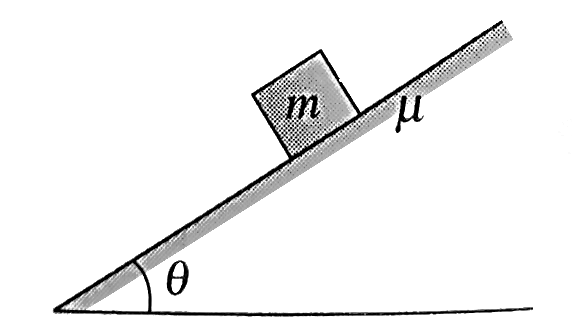 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If `mu=(3)/(4)` then what will be frictional force (shear force) acting between the block and inclined plane when `theta=30^@`:
View Solution
A block B is placed over a cart which in turn lies over a smooth horizontal floor. Block A and Block C are connected to block B with light inextensible strings passing over light frictionless pulleys fixed to the cart as shown. Initially the blocks and the cart are at rest. All the three blocks have mass m and the cart has mass `M(M=3m)`. Now a constant horizontal force of magnitude F is applied to block A towards right.
Assuming friction to be absent everywhere, the magnitude of acceleration of cart at the shoen instant is
View Solution
A block B is placed over a cart which in turn lies over a smooth horizontal floor. Block A and Block C are connected to block B with light inextensible strings passing over light frictionless pulleys fixed to the cart as shown. Initially the blocks and the cart are at rest. All the three blocks have mass m and the cart has mass `M(M=3m)`. Now a constant horizontal force of magnitude F is applied to block A towards right.
Q. Taking friction to be absent every where the magnitude of tension in the string connecting block B and block C is
View Solution
A block B is placed over a cart which in turn lies over a smooth horizontal floor. Block A and Block C are connected to block B with light inextensible strings passing over light frictionless pulleys fixed to the cart as shown. Initially the blocks and the cart are at rest. All the three blocks have mass m and the cart has mass `M(M=3m)`. Now a constant horizontal force of magnitude F is applied to block A towards right.
Q. Let the coefficient of friction between block B and cart is `mu(mugt0)` and friction is absent everywhere else. Then the maximum value of force F applied to block A such that there is no relative acceleration between block B and cart is
View Solution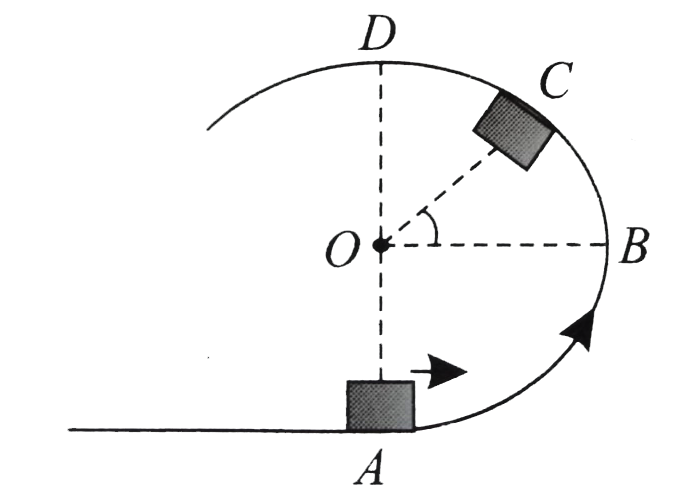
A small block of mass m is pushed on a smooth track from position A with a velocity `(2)/(sqrt(5))` times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
Q. When the block reaches the point B, what is the direction (in terms of angle with horizontal) of acceleration of the block?
View Solution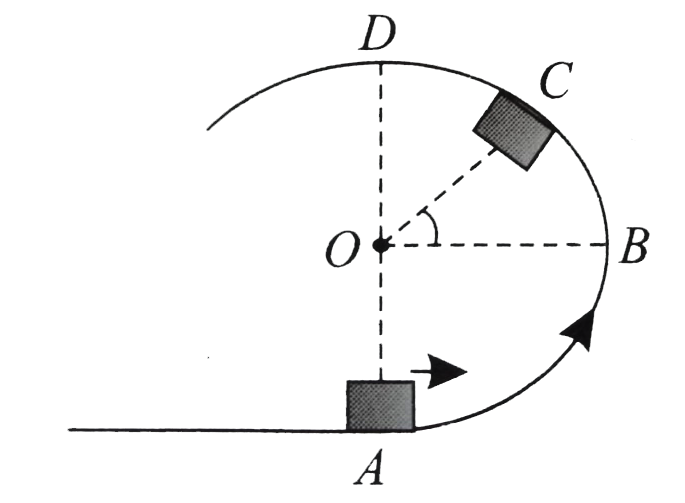
A small block of mass m is pushed on a smooth track from position A with a velocity `(2)/(sqrt(5))` times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
Q. Find where the maximum contact force occurs betwee the block and the track .
View Solution
Comprehension Type questions and complete solutions for chapter CENGAGE PHYSICS DPP of CENGAGE PHYSICS (HINGLISH) of Class 12