Complete Solutions to EXAMPLES of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| CHHAYA PRAKASHINI | EXAMPLES |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
Current I flows through a wire depends on time t as follows`I=3 t^2+2t+5` How much charge flows through the cross section of the wire from t=0 to t=2 s ?
View SolutionIf a current `I=4pi sin pi t` ampere flows through a wire, then find the amount of charge that flows through the wire in (i) t=0 to t=1s and (ii) t=1 s to t=2s.
View SolutionA battery is charged at potential of 15 V for 8 h by means of a current of 10A. While discharging it supplies a current 5A for 15h at a potential difference of 14 V. Calculate the watt-hour efficiency of the battery.
View SolutionThe length,radius and resistivity of two wires are each in the ratio 1:3. The resistance of the comparatively thin wire is `20 Omega`. Determine the resistance of the other wire.
View SolutionIF the length of a copper wire is increased by 0.1%, show that the resistance of the copper wire will increase by 0.2%.
View SolutionA lump of copper of mass 10 g and of density `9g.cm^-3` is given, what should be the length and cross section of the wire made from it so that its resistance is 2 ohm. (Given ,specific resistance of copper `1.8 times 10^-6 Omega cm`).
View SolutionA wire of resistance `5 Omega` is stretched 20%. IF the volume remains constant , find the new resistance.
View SolutionA lump of copper is stretched into a wire 5mn in diameter. Another wire of 1 cm diameter is made from another lump of copper of the same mass. Find the ratio of the resistances of the two wires.
View SolutionThe length of a wire of cylindrical cross section is increased by 100%. Find out the percentage change is the resistance,taking into account the consequent decrease in the diameter of the wire.
View SolutionWhat will be the resistance of a semicircle.[fig.1.7] between points A and B? Given that radial thickness =3cm, axial thickness=4 cm, inner radius=6 cm and resistivity `=4 times 10^-6 Omega` cm.

View SolutionThe temperature coefficient of resistance of copper is `42.5times10^(-4^@)C^-1`. The resistance of a coll of copper at `30^@C` is `8Omega`.What is the resistance at `100^@C`?
View SolutionIF `rho` is the resistivity at temperature T, then the temperature coefficient of resistivity is defined as `alpha=(1drho)/(rhodT)`, which is a constant physical quantity for a given metal, show that `rho=rho_0e^(a(T-T_0)),` where `rho_0` = resistivity at temperature `T_0`.
View SolutionThree resistance of magnitudes `20Omega,30Omega and 40Omega` are connected in series.(i) What is the equivalent resistance? (ii) IF the potential difference across the resistance `20Omega` is 1V, calculate the potential differences across the other two resistances and also the total potential difference across the combination.
View Solution`rho_1` and `rho_2` are the resistivities of the materials of two wires of the same dimensions, what will be the equivalent resistvity of the series combination of the two wires?
View SolutionThe equivalent resistance of two coils connected in series and in parallel are `12Omega` and `5/3 Omega` respectively. Calculate the value of each resistance.
View SolutionA 5 ampere current is distibuted in three branches. The ratio of the lengths of the wires in the three branches is 1:2:3.Determine the magnitude of current in each branch. The material and the cross sectional area of each wire are the same.
View SolutionCurrent is allowed to pass in a circuit formed by two wires of the same material connected in a parallel combination.The ratio of the lengths and the radii of the two wires are 4:3 and 2:3 respectively, Determine the ratio of the current flowing through the two wires.
View SolutionABC is a traingle formed by wires. The resistance of the sides AB,BC and CA are respectively `40 Omega,60 Omega and 100 Omega`. What is the equivalent resistance between the point A and B?

View SolutionDetermine the equivalent resistance between the points A and B [fig.1.13]

View SolutionThe two circuits in the fig.1.14 draw equals currents from the battery.But the current through the resistance R in the second circuit is `1/10`th of that in the first circuit, Determine the values of `R_1` and `R_2`.

View SolutionYou are given several identical resistances,each of value `R= 10 Omega` and each capable of carrying a maximum current of 1A. It is required to make a suitable combination of these resistances to obtain a resistance of `5 Omega` which can carry a current of 4A, FInd the mninimum number of resistances of the type R that will be required.
View SolutionA wire of uniform cross section and length l has a resistance of `16 Omega`. It is cut into four equal parts.Each part is stretched uniformly to length l and all the four streteched parts are connected in parallel. Calculate the total resistance of the combination so formed. Assume that stretching of wire does not cause any change in the density of its material.
View SolutionA resistor is fabricated by connecting two wires of the same material .The radii of the two wires are 1 mm and 3mm respectively and their lengths are 3 cm and 5 cm respectively. IF the two ends of the resistor are connected to the two terminals of a battery of emf 16 V and of negligible Internal resistance, what will be the potential difference between the two ends of the wire of shorter length?
View SolutionA heater of resistance `140 Omega` capable of carrying a current of `1.2 A` is put in a dc mains of 210 V. Find out the minimum value of an additional resistance to be added to run the heater.
View SolutionTo the parallel combination of two resistances `3 Omega` and `1 Omega`, a series combination of resistances `2.15 Omega` and `1 Omega` and a battery are connected. The interval resistance of the battery is `0.1 Omega` and the emf is 2V. Determine the values of current flowing through the resistances. Draw the diagram of the circuit.
View SolutionThe electromotive force of a cell is 2V. The potential difference becomes 1.5 V when a resistance of `15 Omega` is added to the two ends of the cell. Determine the internal resistance of the cell and the lost volt.
View SolutionIn the given diagram [Fig.1.17 (a)], What is the current sent by the battery?
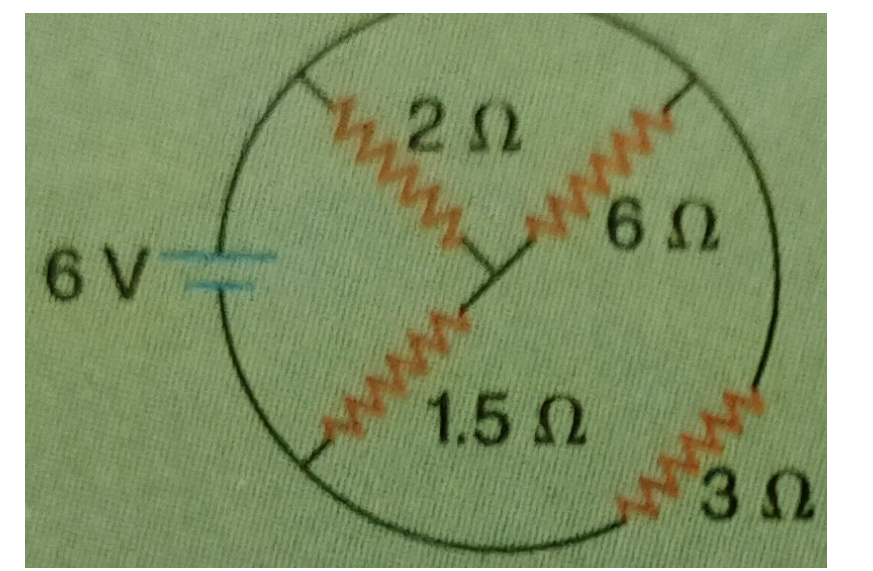
View SolutionTo reduce the action of the galvanometer by 25 times,a shunt is added to it. IF the galvanometer resistance is `1000 Omega` what is the resistance of the stunt?
View SolutionIf a stunt of `1 Omega` is connected to a galvanometer of resistance `99 Omega`, what fraction of the main current will flow through the galvanometer?
View SolutionA battery of internal resistances zero is connected to a galvanometer of resistance `80 Omega` and a resistance of `20 Omega` in series . A current flows through the galvanometer If a shunt of `1 Omega` resistance is connected to the galvanometer, show that the current that will now flow through the galvanometer becomes `1/17` of the previous current.
View SolutionThe internal resistance of a battery of 100 V is `5 Omega`. When the emf of the battery is measured by a voltmeter `20%` error is found. What is the resistance of the voltmeter?
View SolutionIn a supply line of 100 V there is a resistance of `1000 Omega`. In between our terminal of the resistance and its mid point, a voltmeter is connected which gives a reading of 40 V. determine the resistance of the voltmeter.
View SolutionWhen a voltmeter of resistance `100 Omega`is connected with an electric cell, the reading of the voltmeter is 2V. When the cell is connected with a resistance of `15 Omega`. An ammeter of resistance `1 Omega` given the reading of 0.1 A.Determine the emf of the cell.
View SolutionTwo identical cells each of emf 1.5V are connected in series. IF this combination of cells is connected to a resistance and a galvanometer in series, the current that flows through the circuit is 1A.If the cells are connected in parallel the current becomes 0.6 A, Determine the internal resistance of each cell.
View Solution48 similar cells each of emf 1.5V and internal resistance `2 Omega` are used for sending current through a resistance of `6 Omega`. What will be the current if the cells are connected in the following way: 6 rows and 8 cells in a row
View Solution48 similar cells each of emf 1.5V and internal resistance `2 Omega` are used for sending current through a resistance of `6 Omega`. What will be the current if the cells are connected in the following way: 4 rows and 12 cells in a row
View SolutionWhat is the minimum number of cells each of emf 10 V and internal resistance `1 Omega` to pass a current of 10 A through a resistance R of `3 Omega` ? What is the discharging power of R?
View SolutionElectromotive forces of `E_1` and `E_2` [fig:1.28] are respectively 4V and 8V, `r_1=0.5 Omega,r_2=1 Omega`, Determine the current and the terminal potential difference for each cell.
View SolutionA 100V battery has an internal resistance `3 Omega`. What is the reading of a voltmeter having resistance `200 Omega`, when placed across the terminals of the battery? What should be the minimum value of the voltmeter resistance so that the error in finding the emf of the battery may not be more than 1%?
View SolutionA wire of resistance `10 Omega` is used to form a circular ring of circumference 10 cm. IF two current carrying conductors are connected at any two points, the sub circuit so formed has a resistance of `1 Omega`. Find the positions of the two points.
View Solution12 cells each having the same emf are connected in series and are kept in a closed box. Some of the cells are wrongly connected. This battery is connected in series with an ammeter and two similar cells . The current is 3A when the two cells aid the battery and is 2A when the cells and the battery oppose each other. How many cells in the battery are wrongly connected?
View SolutionA cell of emf 1.4V and internal resistance `2 Omega` is connected in series with a resistance of `100 Omega` and an ammeter. The resistance of the ammeter is `4/3 Omega`.To measure the potential difference between the two ends of the resistance a voltmeter is connected .Draw the circuit
View SolutionA cell of emf 1.4V and internal resistance `2 Omega` is connected in series with a resistance of `100 Omega` and an ammeter. The resistance of the ammeter is `4/3 Omega`.To measure the potential difference between the two ends of the resistance a voltmeter is connected IF the reading of the ammter is 0.02 A.what is the resistance of the voltmeter?
View SolutionA cell of emf 1.4V and internal resistance `2 Omega` is connected in series with a resistance of `100 Omega` and an ammeter. The resistance of the ammeter is `4/3 Omega`.To measure the potential difference between the two ends of the resistance a voltmeter is connected IF the reading of the voltmeter is 1.10V, what will be its error?
View SolutionIn the given fig.1.32 what is the equivalent resistance between the two points A and B?

View SolutionA circuit is given in fig.1.34 The emf of the battery is 1.8 V and internal resistance is `2/3 Omega` .Calculate the current through the `3 Omega` resistance.What is the amount of dissipated energy in the whole circuit?

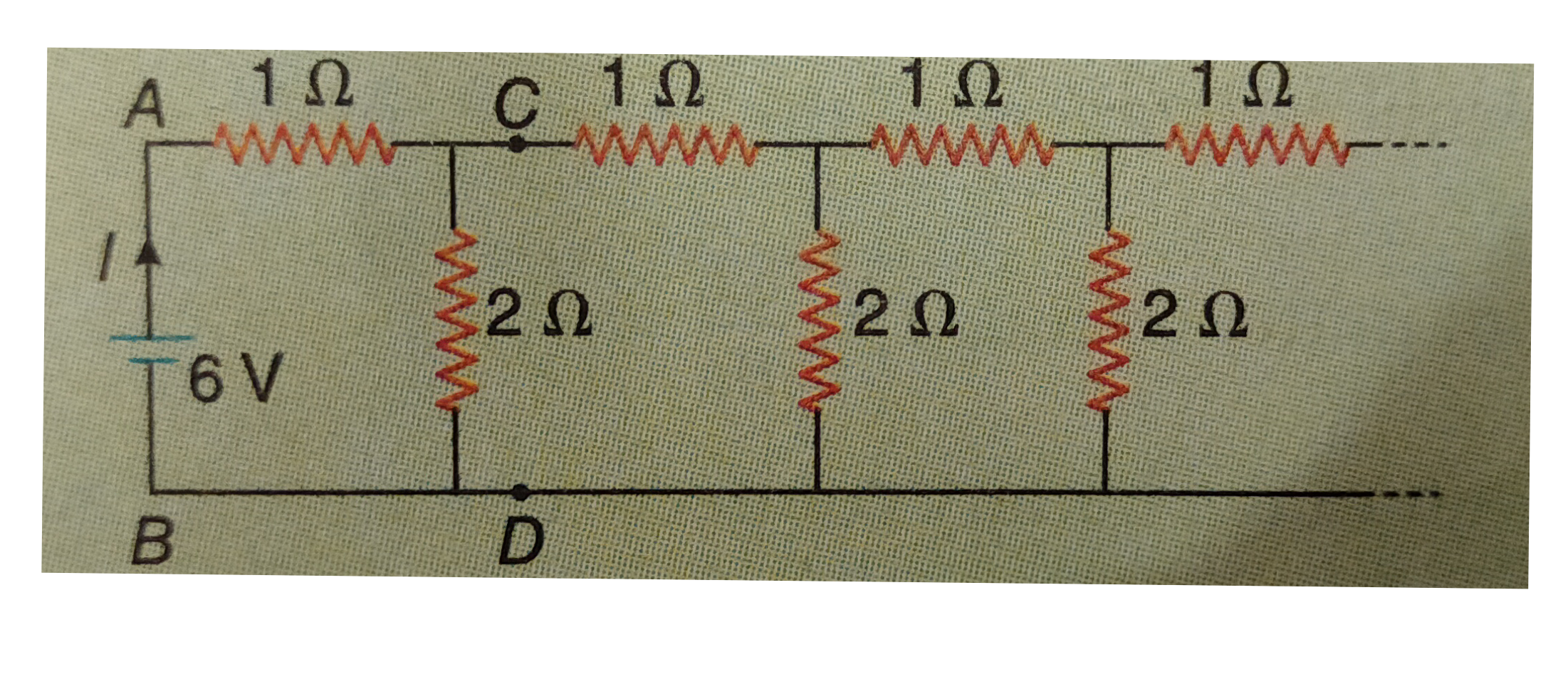
View SolutionAn infinite ladder network of resistances is constructed with `1 Omega` and `2 Omega` resistances as shown in fig. 1.36. The 6V battery A and B has negligible internal resistance. (i) Show that the effective resistance between A and B is `2 Omega` (ii) What is the current that passes through the `2 Omega` resistance nearest to the battery?
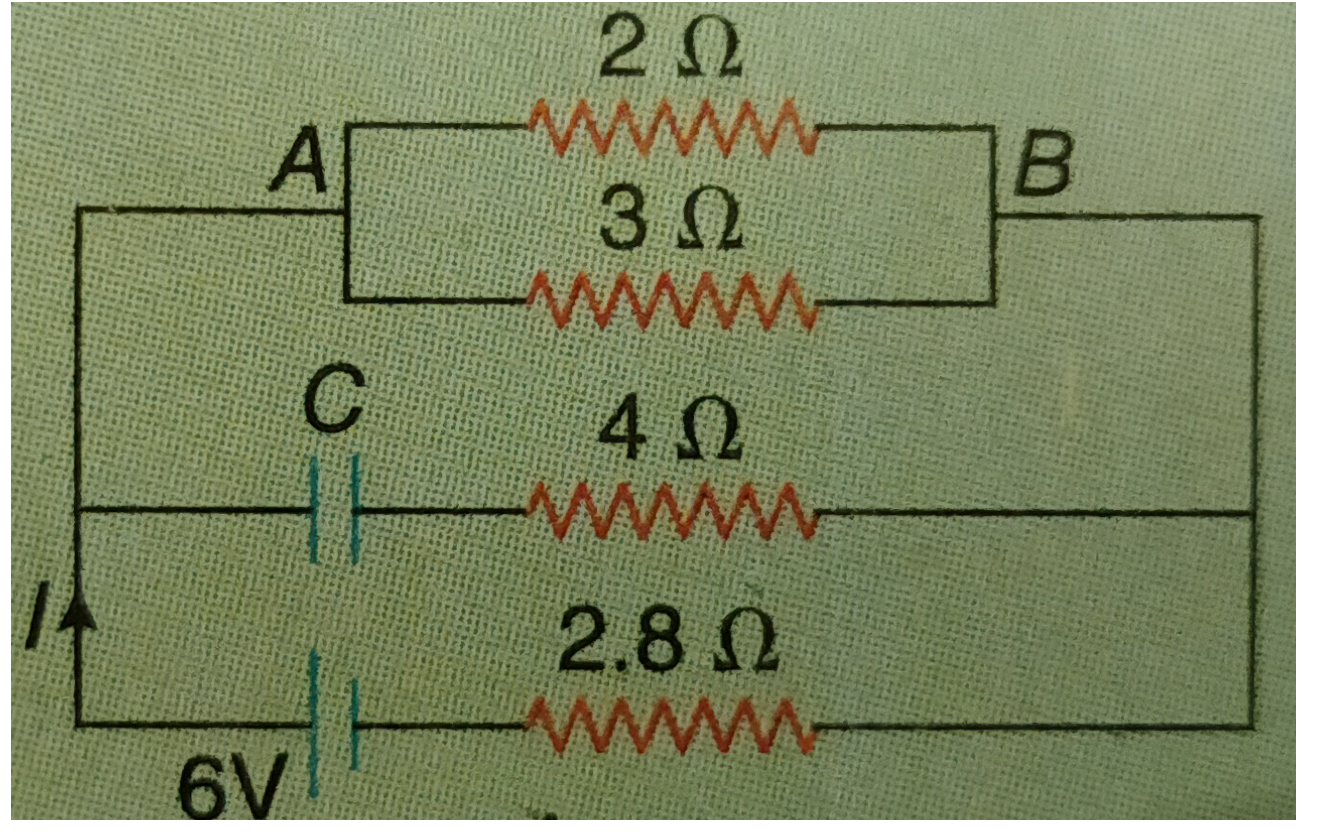
View SolutionIn the circuit shown in the fig.1.38,calculate the first current (dc) through the `2 Omega` resistance. The internal resistance of the battery is negligible and `C=0.2 mu F`.
View SolutionThree resistances A , B and C are connected in such a way that their combined equivalent resistance is equal so that of B. IF A and B are `10 Omega` and `30 Omega` respectively, find the three possible values of C and draw the corresponding circuits.
View SolutionTwo cells one of emf 1.4 V and internal resistance `0.6 Omega` the other of emf 2.5. V and internal resistance `0.3 Omega` are connected in parallel and the combination is connected in series with an external resistance of `4 Omega`. What is the current through this resistance?
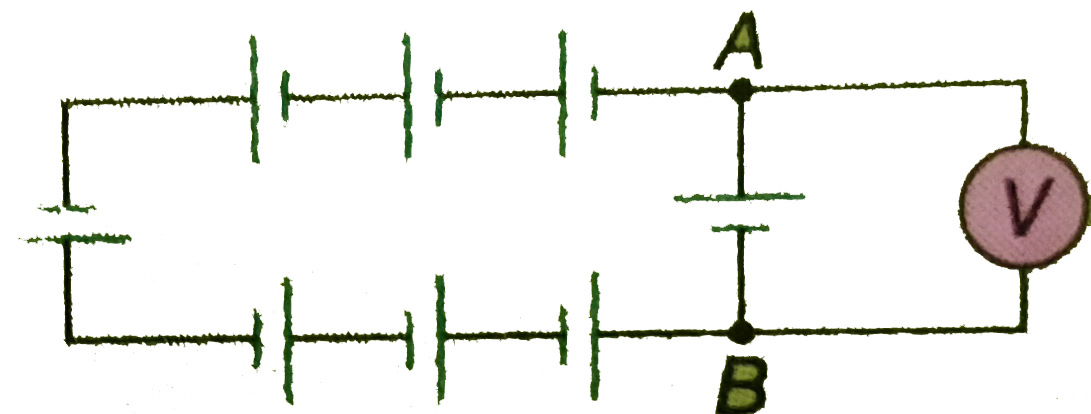
View SolutionIn the circuit fig.1.41 shown, each battery is 5V and has an internal resistance of `0.2 Omega` If the voltmeter is an ideal one, what is its reading?
View SolutionA few storage cells in series are to be charged from a 200 V dc supply. The emf of each cell is 2.5 V, Internal resistance `0.1 Omega` and the charging current is 8A. In this arrangement how many cells can be charged and what extra resistance is required to be conncted in the circuit?
View SolutionA copper wire of cross-sectional area `1 mm^2` carries a current of 0.21A Find the drift velocity of free electrons. Given density of free electrons in copper `=8.84 times 10^(24)m^-3` and electronic charge `e=1.6 times 10^-19 C`.
View SolutionA copper wire of diameter `2/(3sqrtpi)mm` is carrying a current of 1 amp. Calculate the number of free electrons which flow past any cross section of the wire per sec Also find the average speed with which free electrons are flowing in the copper wire assuming that there is one free electron per atom of copper. Number of atmos per `cm^3` of copper `=9 times 10^22`, electronic charge `=1.6 times 10^-19` coulomb.
View SolutionEstimate the average drift speed of conduction electrons in a copper wire of cross sectional area `1 times 10^-7 m^2` carrying a current of 1.5 A.Assume that each copper atom contributes one conduction electron. The density of copper is `9 times 10^3 kg.m^-3` and its atomic mass is `63.5 u`.
View SolutionCompare the drift speed obtained above with (a) thermal speed of electrons carrying the current at room temperature and (b) speed of propagation of electric field along the conductor which causes the drift motion.Avogadro's number=`6.0 times 10^26` per kg atom. Boltzmanm constant , `k=1.38 times 10^-23 J.K^-1` mass of electron `=9.1 times 10^-31 kg`.
View SolutionWhen an iron wire of diameter 1 cm is copper plated uniformly. Resistance of iron reduces to `1/3` of its original value. Calculate the thickness of copper plating, Resistivities of copper and iron are `1.8 times 10^-6 Omega`.cm and `1.98 times 10^-5 Omega`.cm respectively.
View SolutionIn an aluminimum (Al) bar of square cross section, a square hole is drilled and is filled with iron (Fe) as shown in the figure. The electrical resistivities of AL and Fe are `2.7 times 10^-8 Omega`.m and `10 times 10^-8 Omega` m respectively. Calculate the electrical resistance between the two faces P and Q of the composite bar.

View SolutionA conductor of resistance `20 Omega` having uniform cross sectional area is bent in the form of a closed ring. A cell of emf 1.5 V and of negligible internal resistance is joined to the ring between two points dividing the circumference of the ring in the ratio 3:1 Find the currents flowing through the two parts of the ring .
View Solution
EXAMPLES questions and complete solutions for chapter CURRENT ELECTRICITY of CHHAYA PHYSICS (BENGALI ENGLISH) of Class 12
All Exercises from CHHAYA PRAKASHINI Class 12 PHYSICS CURRENT ELECTRICITY
- CBSE SCANNER
- ENTRANCE CORNER(ASSERTION REASON TYPE)
- ENTRANCE CORNER(COMPREHENSION TYPE)
- ENTRANCE CORNER(INTEGER ANSWER TYPE)
- ENTRANCE CORNER(MULTIPLE CORRECT ANSWERS TYPE)
- EXAMINATION ARCHIVE WITH SOLUTIONS(AIPMT)
- EXAMINATION ARCHIVE WITH SOLUTIONS(JEE MAIN)
- EXAMINATION ARCHIVE WITH SOLUTIONS(NEET)
- EXAMINATION ARCHIVE WITH SOLUTIONS(WBCHSE)
- EXAMINATION ARCHIVE WITH SOLUTIONS(WBJEE)
- EXAMPLES
- EXERCISE ( HOT NUMERICAL PROBLEMS)
- EXERCISE ( MULTIPLE CHOICE QUESTION)
- EXERCISE ( PROBLEM SET-I)
- EXERCISE ( PROBLEM SET-II)
- EXERCISE ( SHORT ANSWER TYPE QUESTION-I)
- EXERCISE ( SHORT ANSWER TYPE QUESTION-II)
- EXERCISE ( VERY SHORT ANSWER TYPE QUESTION)
- HIGHER ORDER THINKING SKILL (HOTS) QUESTION
- NCERT EXEMPLAR QUESTION WITH ANSWER HINT(MCQ-1)
- NCERT EXEMPLAR QUESTION WITH ANSWER HINT(MCQ-2)
- NCERT TEXTBOOK QUESTION WITH ANSWER HINT