An infinite ladder network of resistances is constructed with 1Ω and 2Ω resistances as shown in fig. 1.36. The 6V battery A and B has negligible internal resistance. (i) Show that the effective resistance between A and B is 2Ω (ii) What is the current that passes through the 2Ω resistance nearest to the battery?
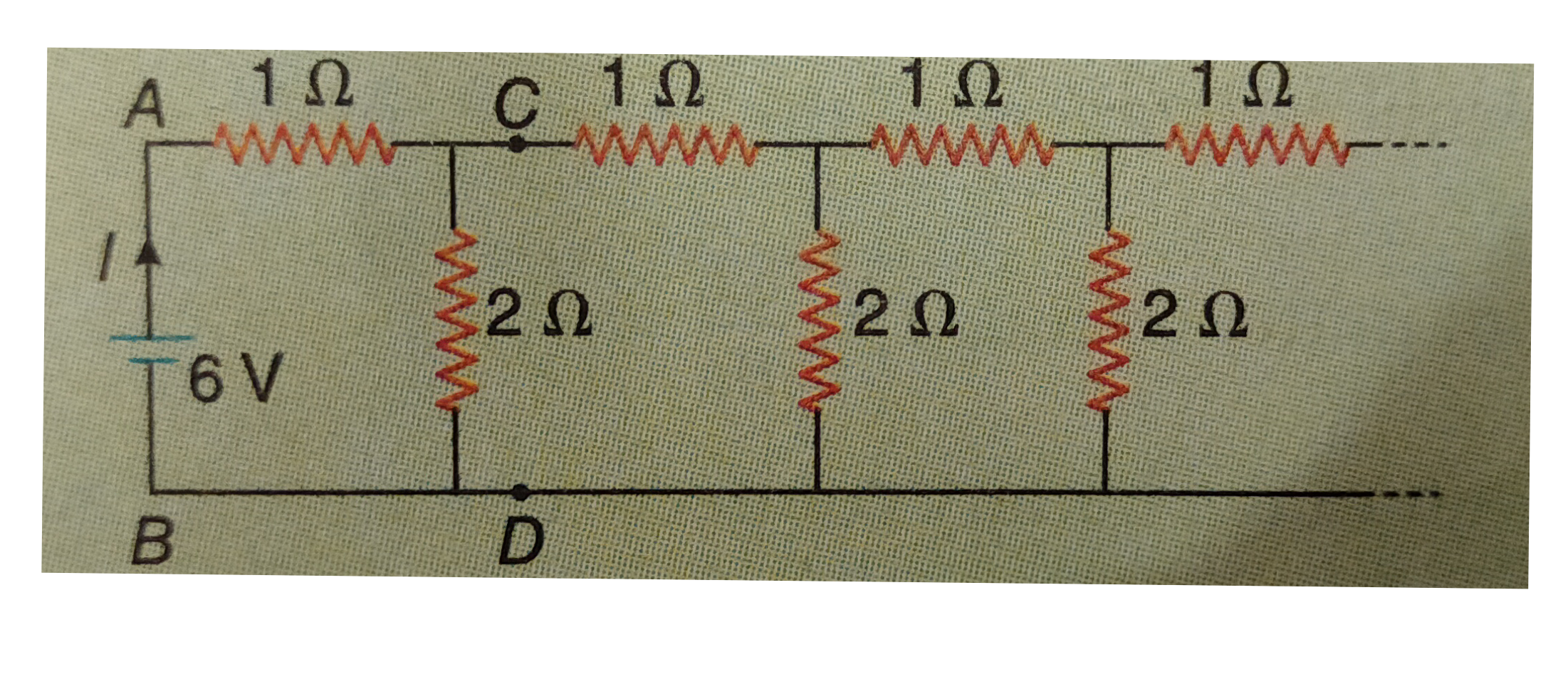
Suppose effective resistance between A and B =R. From the fig.1.36 it is clear that on the right side of CD the infinite network is equivalent to that on the right side of AB,because deleting one chain does not affect the equivalent resistance R. So the circuit shown in the fig.1.37 is the equivalent circuit of the fig.1.36.
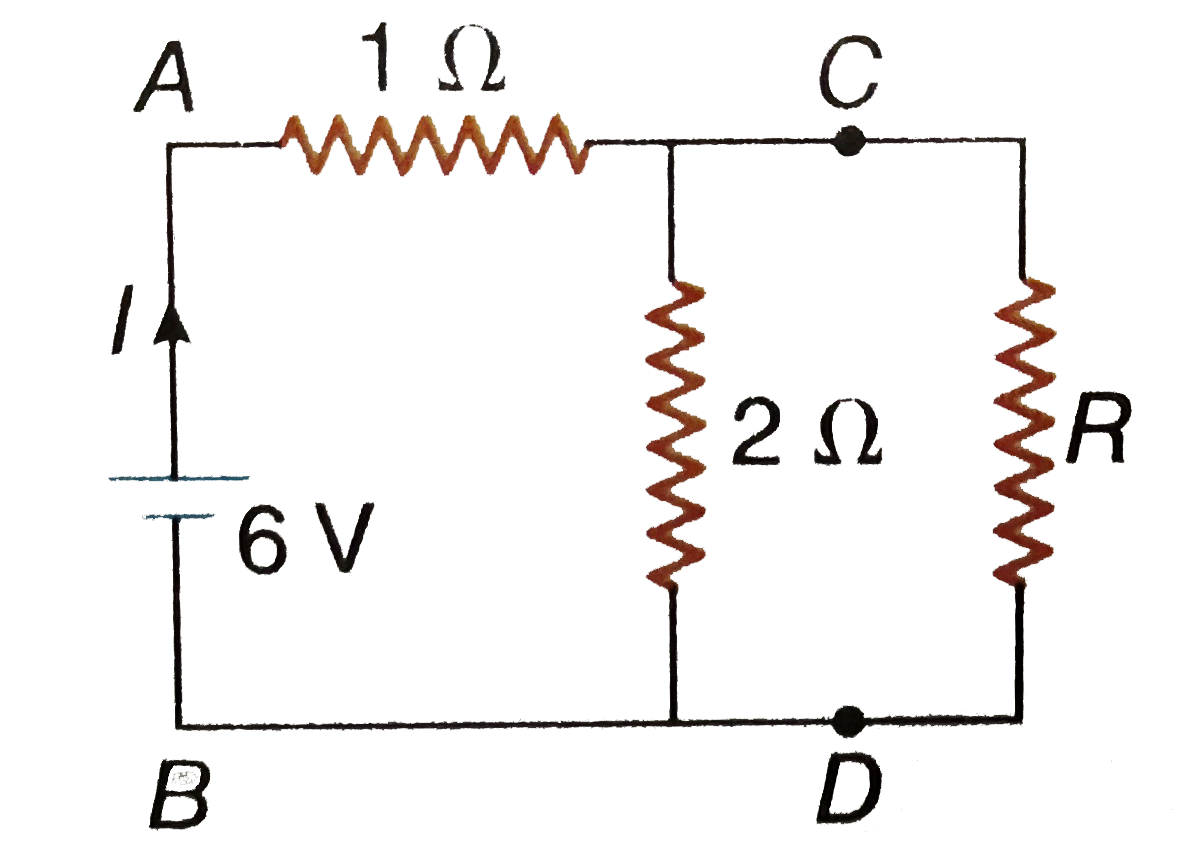
(i) From the fig.1.37 effective resistance between A and B is
R=1+2R1+Ror,R=2+3R2+R
or,R2−R−2=0or,(R+1)(R−2)=0
Obviously R≠−1
Hence , R=2 Ω
(ii) Main current , I=6R=62=3A
∴VAC=I×1=3×1=3V
∴VCD=6−3=3V
So, current through the 2Ω resistance nearest to the battery
VCD3=32=1.5A.
Topper's Solved these Questions
- CURRENT ELECTRICITY BOOK - CHHAYA PUBLICATIONCHAPTER - CURRENT ELECTRICITY EXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTION
26 Videos
- CURRENT ELECTRICITY BOOK - CHHAYA PUBLICATIONCHAPTER - CURRENT ELECTRICITY EXERCISE - NCERT TEXTBOOK QUESTION WITH ANSWER HINT
4 Videos
- COMMUNICATION STSTEMBOOK - CHHAYA PUBLICATIONCHAPTER - COMMUNICATION STSTEMEXERCISE - CBSE SCANNER
28 Videos
- DIFFRACTION AND POLARISATION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - DIFFRACTION AND POLARISATION OF LIGHTEXERCISE - CBSE SCANNER
27 Videos
Similar Questions
Knowledge Check
An infinite ladder network is constructed with 1Ωand 2Ω resistors as shown. Find the equivalent resistance points A and B.
 A1ΩB2ΩC3ΩD4Ω
A1ΩB2ΩC3ΩD4Ω
An infinite ladder network is constructed with 1Ωand 2Ω resistors as shown. Find the equivalent resistance points A and B.

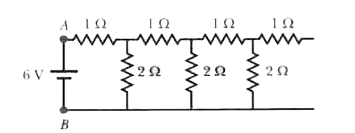
View SolutionAn infinite ladder is constructed with 1(Ω)and 2(Ω)resistor as shown in figure.(a)Find the effective resistance between the point A and B. (b) Find the current that passes through the (2Ω) resistor nearest to the battery.

View SolutionAn infinite ladder is constructed with 1(Ω)and 2(Ω)resistor as shown in figure.(a)Find the effective resistance between the point A and B. (b) Find the current that passes through the (2Ω) resistor nearest to the battery.

View SolutionAn infinite ladder is constructed with 1Ωand2Ω resistors as shown in Fig 27-49. Find the effective resistance between the points A and B.
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA 10 V battery of negilgible internal resistance is connected across a 200V battery and a resistance of 38Ω as shown in figure.
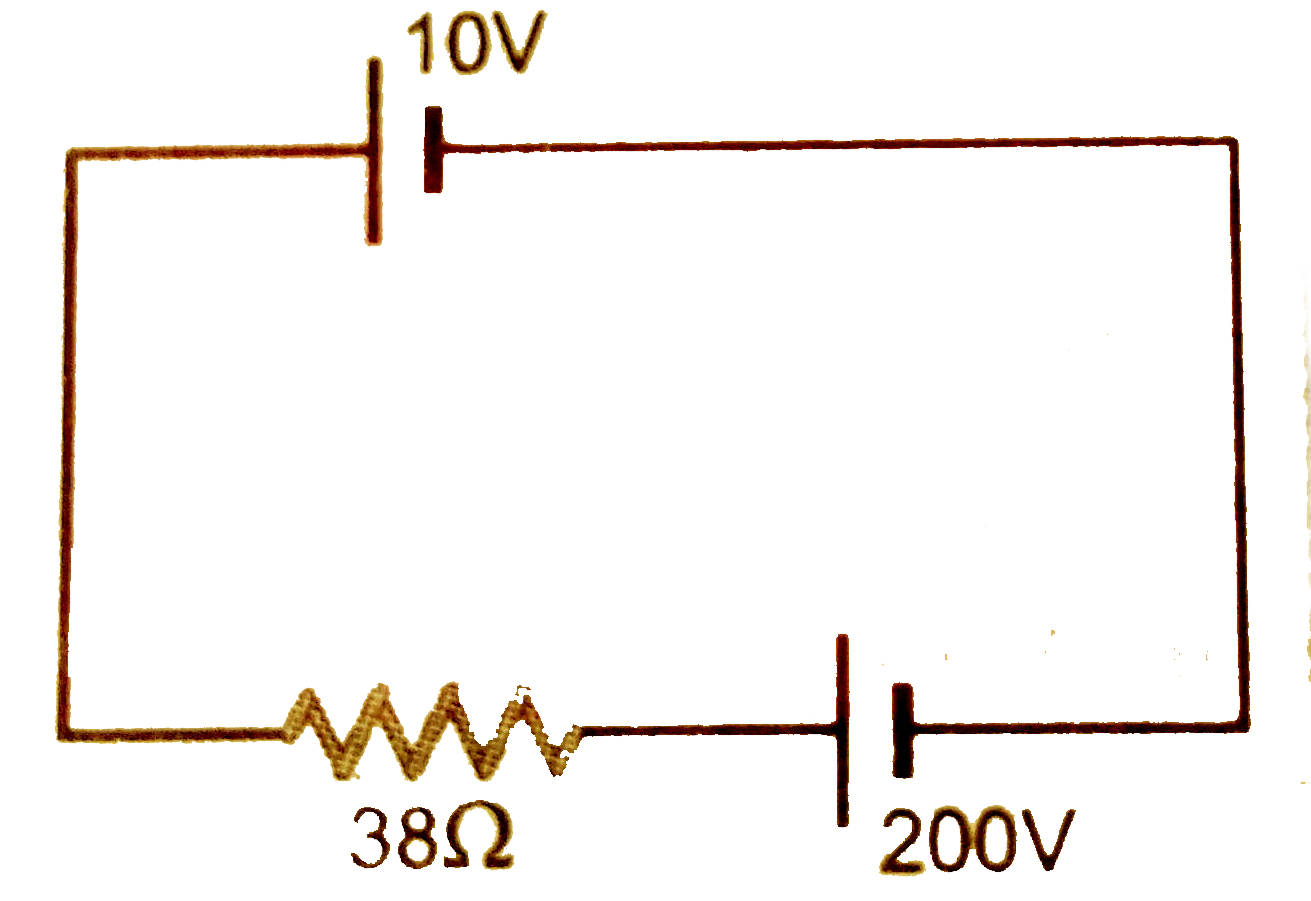 . Find the value of current in the circuit.
. Find the value of current in the circuit.
View Solution

