Complete Solutions to All Questions of chapter CIRCULAR,ROTATIONAL & SIMPLE HARMONIC MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CIRCULAR,ROTATIONAL & SIMPLE HARMONIC MOTION |
| D MUKHERJEE | All Questions |
| Number Of Questions | 88 |
| Academic Year | 2023-24 |
A particle of mass m is tied to light string and rotated with a speed v along a circular path of radius r. If T=tension in the string and `mg=` gravitational force on the particle then actual forces acting on the particle are
View SolutionA particle of mass m is tied to a light string of length l and rotated along a vertical circular path. What should be the minimum speed at the highest point of its path so that the string does not become slack at any position ?
View SolutionA simple pendulum has a string of length l and bob of mass m. When the bob is at its lowest position , it is given the minimum horizontal speed necessary for it to move in a circular path about the point point of suspension. The tension in the string at the lowest position if the bob is
View SolutionIn the previous question, when the string is horizontal, the net force on the bob is
View SolutionIn a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle `theta` with the vertical.
View SolutionA particle of mass m is fixed to me one end of a light right rod of length l and rotated in a vertical circular path about its other end. The minmum speed of the particle at its highest point must be
View SolutionIn the previous question, if the particle is released from rest at its highest position then the tension in the road
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity `omega` in gravity free space. The increase in length of the spring is

View SolutionA particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration `a_(c)` is varying with time t as `a_(c) = k^(2)rt^(2)`, where k is a constant. The power delivered to the particle by the forces acting on it is :
View SolutionA car is moving in a circular horizonta track of radius 10m with a constant speed of 10 m/s. A pendulum bob is suspended from the roof of the cat by a light rigid rod of length 1.00m. The angle made by the rod with track is
View Solution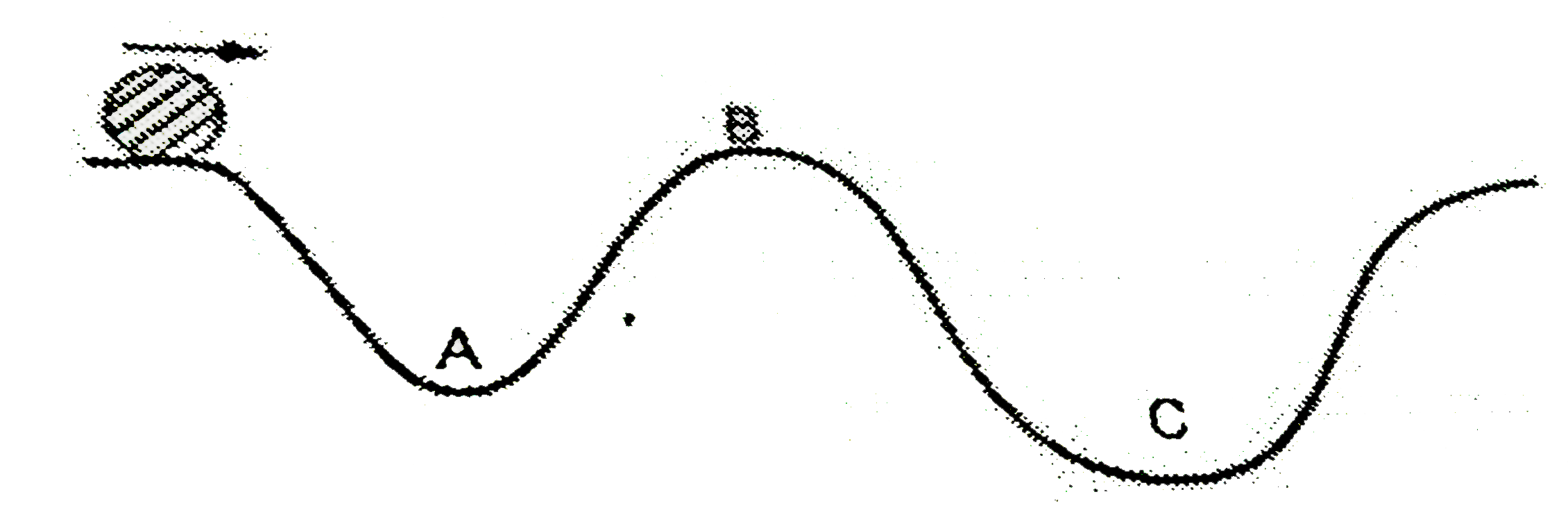
A body moves along an uneven horizontal road surface with constant speed at all points. The normal reaction of the road on the body is
View SolutionIn gravity free space, a particle is in constant with the inner surface of a hallow cylinder and moves in a circular path along the surface. There is some friction between the particles and the surface. The retardation of the particle is :
View SolutionThe narrow tube AC forms a quarter circles in a vertical plane. A ball B has an area of cross-section slighly smaller than that of the tube and can move without friction through it. B is placed at A and displaced slightly. During the motion from A to C it will :

View SolutionA car moves along a horizontal circular road of radius r with constant speed v. The coefficient of friction between the wheels and the road is `mu`. Which of the following statement is not true ?
View SolutionWhen a car negotiates a curve, the normal force exerted on the inner and outer wheels are `N_(2)` and `N_(1)` respectively. Then `N_(1)//N_(2)` is
View SolutionA curved section of a road is banked for a speed `v`. If there is no friction between the road and the tyres then.
View SolutionA cyckist moves along a curved road with a velocity `v`. The road is banked for speed `v`. The angle of banking is `theta`. Which of the following statement is not true?
View SolutionTwo point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
View SolutionA man stands at one end of a boat which is stationary in water. Neglect water resistance. The man now moves to the other end of the boat and again becomes stationary. The centre of mass of the man plus boat system will remain stationary with respect to water.
View SolutionA strick is thrown in the air and lands on the ground at some distance from the centre of mass of the stick will move along a paranolic path
View SolutionA man hangs from a rope attached to a hot-air balloon. The mass of the man is greater than the mass of the balloon and its constents. The system is stationary in air. If the man now clims up to the balloon using the rope, the centre of mass of the man plus balloon system will
View SolutionThere are some passeger inside a stationary railway compartment. The centre of mass of the compartment itself (without the passngers) is `C_(1)` while the centre of mass of the compartment plus passengers system is `C_(2)` if passenger move about inside the comparment
View SolutionFor a system to be in equilibrium, the torques acting on it must balance. This is true only if the torques are taken about
View SolutionA uniform horizontal meter scale of mass m is susopended by two certical string attached to its two ends. A body of mass 2m is place on the `75-cm` mark. The tensions in the two strings are in the ratio
View SolutionThe line of action of the resultant of two like parallel forces shifts by one-fourth of the distance between the forces when the two forces are interchanged. The ratio of the two forces is:
View SolutionA rectangular block has a square base measuring `axxa` , and its height is h. It moves with a speed v on a smooth horizontal surface.
View SolutionA rectangular block has a square base measuring `axxa` and its height is `h`. It moves on a horizontal surface in a direction perpendicular to one of the edges. The coefficient of friction is `mu`. It will topple if
View SolutionA flywheel rotates with a uniform angular acceleration. Its angular velocity increases from `20pi rad//s` to `40pi rad //s` in 10 seconds. How many rotations did it make in this period ?
View SolutionWhen a ceiling fan is switched on, it makes 10 rotations in the first 3 seconds. Assuming a uniform angular acceleration, how many rotation it will make in the next 3 seconds?
View SolutionWhen a celling fan is switched off, its angular velocity falls to half while it makes `36` rotations. How many more rotations will it make before coming to rest ?
View SolutionA flywheel rotates about an axis. Due to friction at the axis, it experiences an angular retardation proportional to its angular velocity. If its angular velocity falls to half while it makes `n` rotations, how many more rotations will it make before coming to rest?
View SolutionAn external device, e.g an electric motor supplies constant power to a rotating system e.g., a flywheel through a torque `tau` power angular velocity of the system is `omega` Both `tau` and `omega` are variable
View SolutionTwo identical rods are joined to form an `'X'`. The smaller angle between the rods is `theta`. The moment of inertia of the system about an axis passing through point of intersection of the rods and perpendicular to their plane is proportional to:
View SolutionA uniform rod of mass m and length l makes a constant angle `theta` with an axis of rotation which passes through one end of the rod. Its moment of inertia about this axis is
View SolutionA disc of mass `m` and radius `R` has a concentric hole of radius `r`. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionThe radius of gyration of a thin disc of radius 4 cm about a diameter is
View SolutionThe radius of gyration of a solid shapere of radius r about a certain axis is r. The distance of this axis from the centre of the shpere is
View SolutionThree identical rods, each of length `L`, are joined to form a rigid equilateral triangle. Its radius of gyration about an axis passing thorugh a corner and perpendicular to plane of triangle is
View SolutionLet `I` be the moment of interia of a uniform square plate about an axis `AB` that passses through its centre and is parallel to two its sides. `CD` is a line in the plane of the plate that passes through the centre of the plate and makes an angle `theta` with `AB`. The moment of inertia of the plate about the axis `CD` is then equal to-
View SolutionIf radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionA man spinning in free space can change the moment of inrtia of his body (I) by charging its shape. In this process,
View SolutionA small ball strikes a stationery uniform rod, which is free to rotate, in gravity-free space. The ball does not stick to the rod. The rod will rotate about
View SolutionThree identical solid spheres move down three incline `A, B` and `C` are all of the same dimensions. A is without friction, the friction between `B` and a sphere is sufficient to cause rolling without slipping, the friction between `C` and a sphere causes rolling with slipping. The kinetic energies, of `A, B, C` at the bottom of the inclines are `E_(A),E_(B),E_(C)`.
View SolutionA mass m moving with a constant velocity along a line parallel to the axis, away from the origin. Its anguarl momentum with respect to the origin
View SolutionA stone of mass m tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by `T = Ar^n` where A is a constant, r is the instantaneous radius of the circle and n=....
View SolutionFor a particle undergoing SHM, the velocity is plotted aginst displacement. The curve will be
View SolutionA particle undergoes `SHM` with a time period of `2` second in how much time it travel from its mean position to a displacement equal to half of its amplitude?
View SolutionTwo blocks of masses `m_1` and `m_2` are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block `(m_2)` drops off. The other block `(m_1)` will

View SolutionThe displacement `y` of a particle executing periodic motion is given by `y = 4 cos^(2) ((1)/(2)t) sin(1000t)`
This expression may be considereed to be a result of the superposition of
View SolutionA simple pendulum has a bob of mass `m` and swings with an angular amplitude `phi`. The tension in thread is `T`. At a certain time the string makes an angle `theta` with the vertical `(theta le phi)`
View SolutionA simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle `theta` with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
View SolutionA stone tied to a string of length `L` is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time the stone is at lowest position and has a speed `u` . Find the magnitude of the change in its velocity as it reaches a position, where the string is horizontal.
View SolutionA particle `P` of mass `m` is attached to a vertical axis by two strings `AP` and `BP` of legth `l` each. The separation `AB=l`, rotates around the axis with an angular velocity `omega`. The tension in the two string are `T_(1)` and `T_(2)`. Then
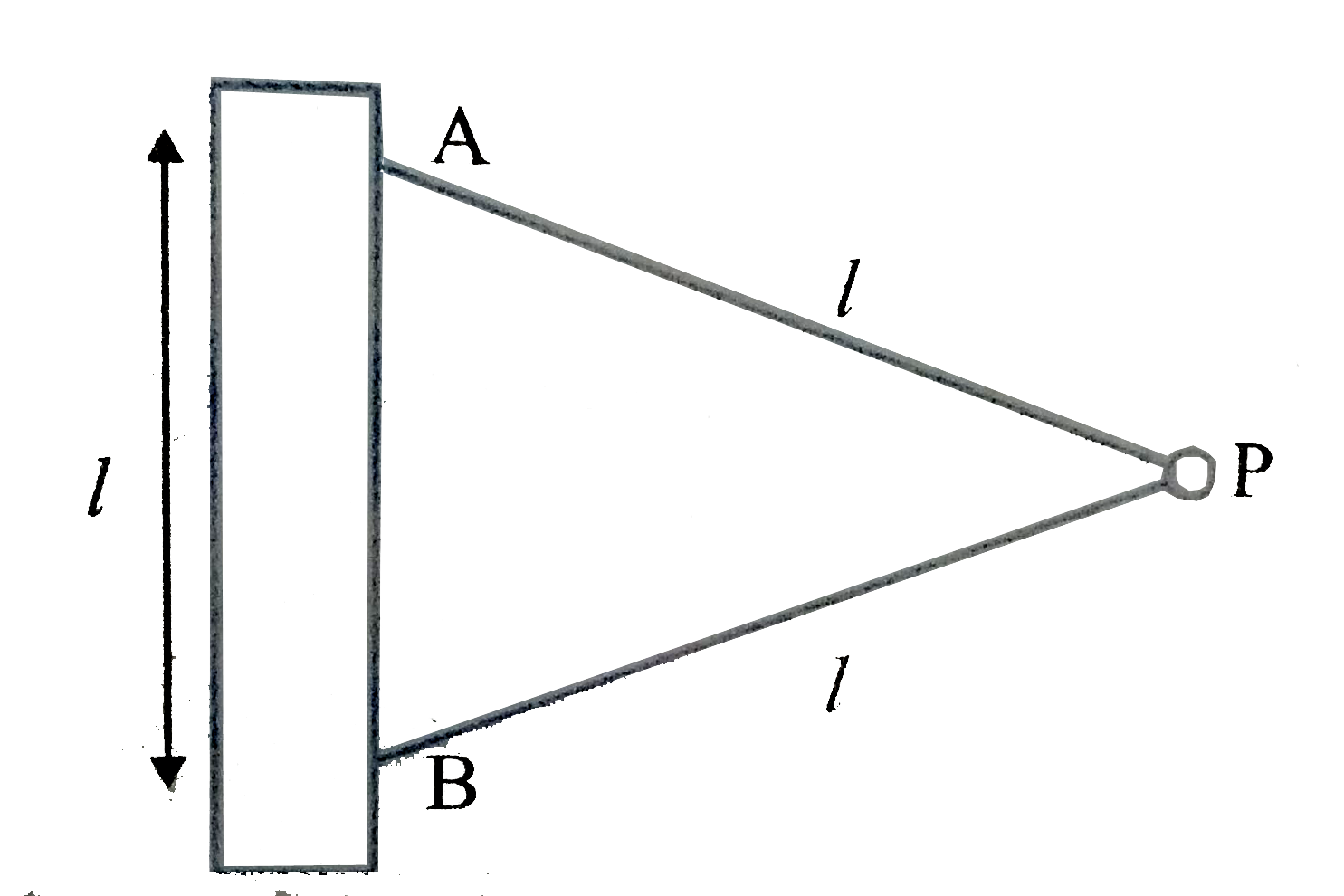
View SolutionA uniform rod of mass `m` and length `l` rotates in a horizontal plane with an angular velocity `omega` about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA tube of length L is filled completely with an incomeressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity `omega.` The force exerted by the liquid at the other end is
View SolutionA ring of mass `m` and radius `R` is being rotated about its axis with constant angular velocity `omega` in the gravity free space. Find tension in the ring.
View Solution`ABCDE` is a smooth iron track in the vertical plane. The sections `ABC` and `CDE` are quarter circles. Points `B` and `D` are very close to `C.M` is a small magnet of mass `m`. The force of attraction between `M` and the track is `F`, which is constant and always normal to the track. `M` starts from rest at `A`, then:
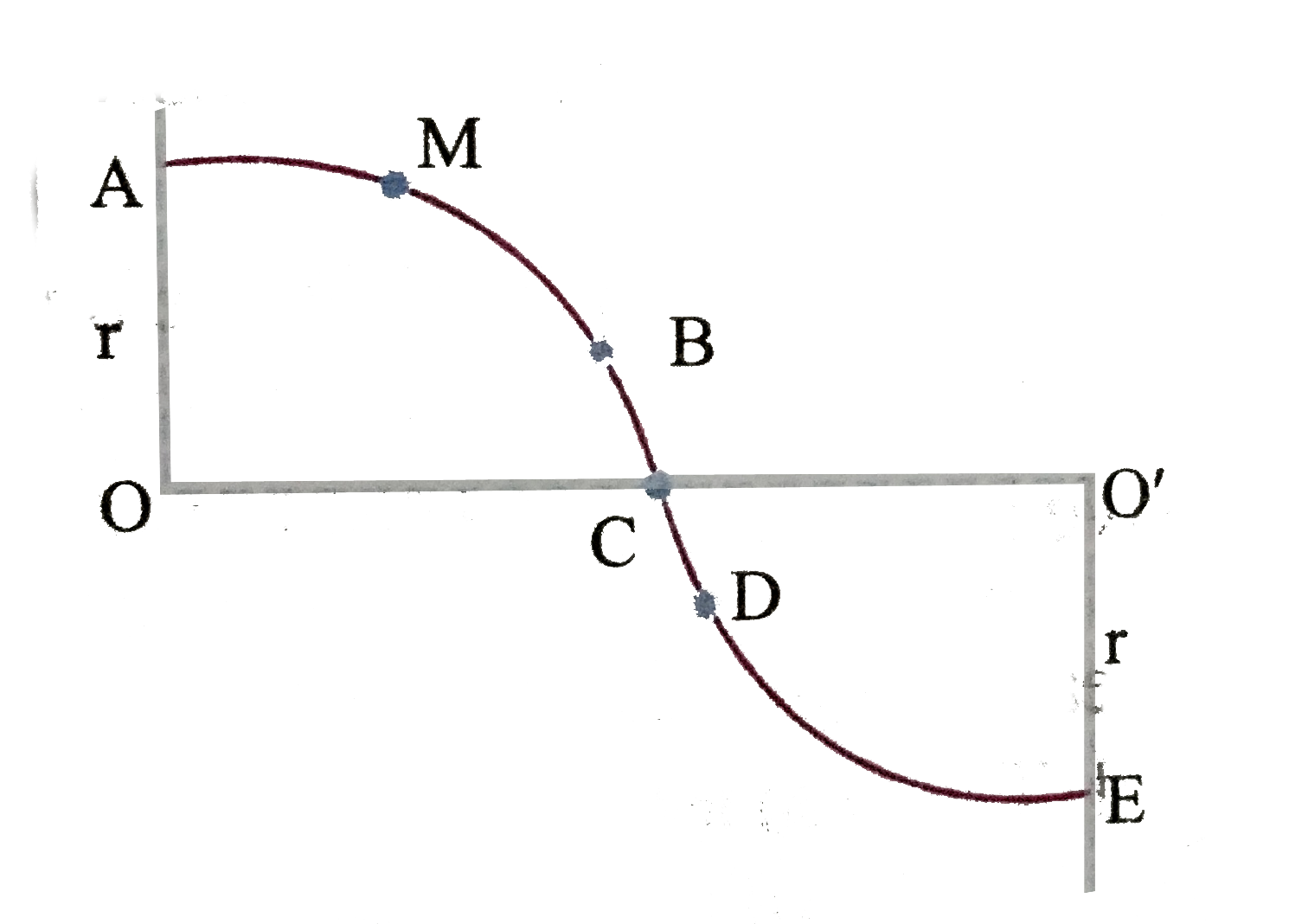
View SolutionThe earth rotates from west to east. A wind mass begins movings due north from the equator, along the earth's surface. Neglect all effects other than the rotation of the earth. The wind mass will
View SolutionA geostationary staellite S is stationed above a point P on equator. A particle is fired from S directly towards P.
View SolutionA body moves on a horizontal circular road of radius `r`, with a tangential acceleration `a_(t)`. The coefficient of friction between the body and the road surface Is `mu`. It begins to slip when its speed is `v`.
(i) `v^(2)=murg`
(ii) `mug=(v^(4)/(r^92))+a_(t))`
(iii) `mu^(2)g^(2)=(v^(4)/(r^(2)+a_(t)^(2))`
(iv) The force of friction makes an angle `tan^(-1)(v^(2)//a_(t)r)` with the direction of motion at the point of slipping.
View SolutionThe density of a rod AB increases linearly from A to B its midpoint is O and its centre of mass is at C. four axes pass through A, B, O and C, all perpendicular to the length of the rod. The moment of inertial of the rod about these axes are `I_(A), I_(B), I_(O)` and `I_(C)` respectively.
View SolutionA square plate lies in the xy plane with its centre at the origin and its edges parallel to the x and y axes. Its moments of inertia about the x, y and z axes are `I_(x), I_(y)` and `I_(Z)` respectively, and about a diagonal it is `I_(D)`
View SolutionFour identical rods each of mass `m` and length `l` are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about
View SolutionP is the centre of mass of four point masses A,B, C and D which are lying in the same length but not along the same straight line then.
View SolutionWhen slightly different weights are placed on the two pans of a beam balance, the beam comes to rest at an angle with the horizontal. The beam is supported at a single point P by a pivot.
View SolutionA body is in equilibrium under the influence of a number of forces. Each has a different line of action. The minimum number of forces required is.
View SolutionA block with a square base measuring axa and height `h`, is placed on an inclined place. The coefficient of friction is `m`. The angle of inclination `(theta)` of the plane is gradually increased. The block will.
View SolutionTwo men support a uniform horizontal beam at its two ends, if one of them suddenly lets go, the force exerted by the beam on the other man will
View SolutionA man spinning in free space changes the shape of his body, eg. By spreading his arms or curling up. By doing this, he can change his.
View SolutionA man standing on a platform holds weights in his outstretched arms. The system is rotated about a central vertical axis. If the man now pulls the weights inwards close to his body then
View SolutionA horizontal disc rotates freely about a vertical axis through its centre. A ring, having the same mass and radius as the disc, is now gently placed on the disc. After some time, the two rotate with a common angular velocity, then
View SolutionTwo horizontal discs of different radii are free to rotate about their central vertical axes: One is given some angular velocity, the other is stationary. Their rims arc now brought in contact. There is friction between the rims. Then
View SolutionA constant external torque `tau` acts for a very brief period `/_\t` on a rotating system having moment of inertia `I` then
View SolutionTwo identical spheres `A` and `B` are free to move and I, rotate about their centres. They are given the same impel `J`. The lines of action of the impulses pass through tht centre of `A` and away from the centre of `B`, then
View SolutionThe motion of a sphere moving on a rough horizontal surface changes from pure sliding (without rolling) to pure rolling (without slipping). In this process, the force of friction
(`i`) intially acts opposite to the direction of motion and late in the direction of motion
(`ii`) cause linear retardation
(`iii`) causes angular acceleration
(`iv`) stops acting when pure rolling begins
View SolutionA disc of circumference `s` is at rest at a point `A` on a horizontal surface when a constant horizontal force begins to act on its centre. Between `A` and `B` there is sufficient friction toprevent slipping, and the surface is smooth to the right of `B.AB = s`. The disc moves from `A` to `B` in time `T`. To the right of `B`,
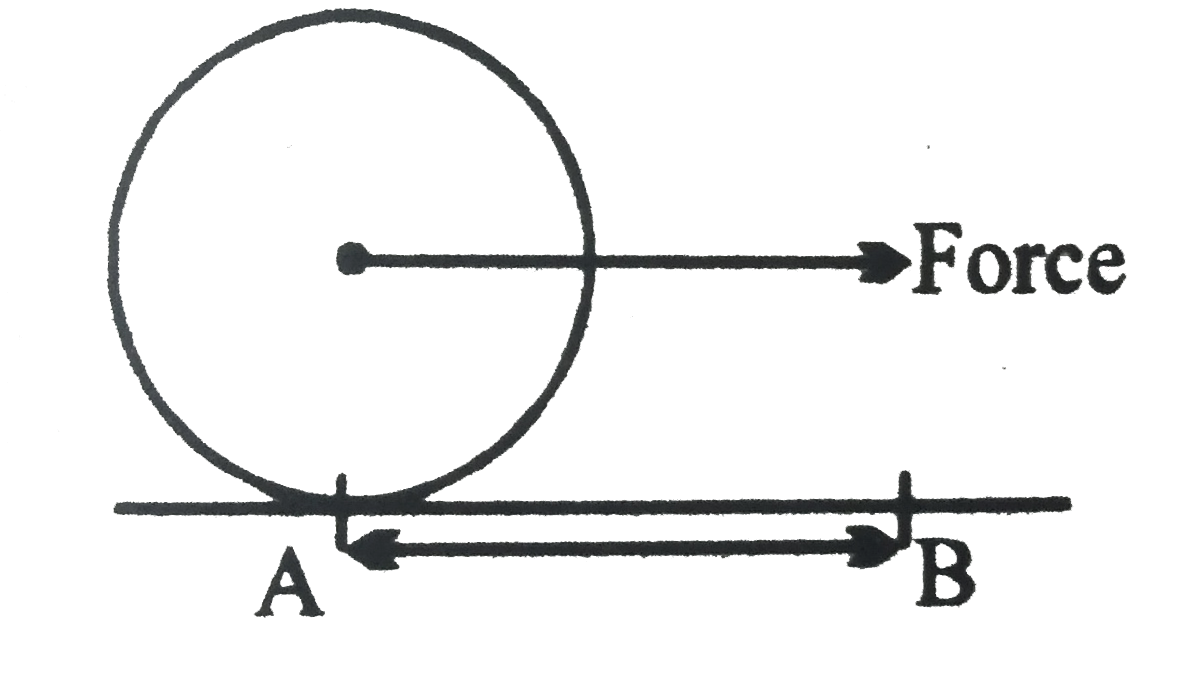 .
.
View SolutionA ring (`R`), a disc (`D`), a solid sphere (`S`) and a hollow sphere with thin walls (`H`), all having the same mass but different radii, start together from rest at the top of inclined plane and roll down without slipping. Then
View SolutionA solid sphere rolls without slipping on a rough horizontal floor, moving with a speed `v`. It makes an elastic collision with a smooth vertical wall. After impact
View SolutionA sphere `S` rolls without slipping with a constant speed on a plank `P`. The friction between the upper surface of `P` and the sphere is sufficient to prevent slipping, while the lower surface of `P` is smooth and rest on the ground. Initially `P` is fixed on the ground by a pin `N`. If `N` is suddenly removed

View SolutionA ring rolls without slipping on the ground. Its centre `C` moves with a constant speed `u.P` is any point on the ring. The speed of `P` with respect to the ground is `v`.
View Solution
A uniform circular ring rolls without slipping on a horizontal surface. At any instant, its position is as shown in the figure. Then
View SolutionA wheel of radius `r` rolls without slipping with a speed `v` on a horizontal road. When it is at a point `A` on the road, a small blob of mud separates from'the wheel at- its highest point and lands at point `B` on the road:
View SolutionIn the figure, the disc `D` does not slip on the surface `S`, the pulley `P` has mass and the string does not slip on it. The string is wound around the disc.

View Solution
A spring block system undergoes SHM on a smooth horizontal surface, the block is now given some charge and a uniform horizontal electric field E is switched on as shown in Fig. As a result
View SolutionA simple pendulum has a time period T. The bob is now given some positive charge –
(1) If some positive charge is placed at the point of suspension, T will increases
(2) If some positive charge is placed at the point of suspension, T will not change
(3) If a uniform downward electric field is switched on, T will increase
(4) If a uniform downward electric field is switched on, T will decrease
View SolutionA coin is placed on a horizontal platform, which undergoes horizontal simple harmonic motion about a mean position O. The coin does not slip on the platform. The force of friction acting on the coin is F.
(i) F is always directed towards O
(ii) F is directed towards O when the coin is moving away from O, and away from O when the coin moves towards O
(iii) `F=0` when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
(iv) F is maximum when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
View SolutionIn the previous question, the angular frequency of the simple harmonic motion is `omega`. The coefficient of friction between the coin and the platform is `mu`. The amplitude of oscillation is gradually increased. The coin will begin to slip on the platform for the first time
(i) at the extreme positions of oscillations
(ii) at the mean position
(iii) for an amplitude of `(mug)/(omega^2)`
(iv) for an amplitude of `(g)/(muomega^2)`
View SolutionA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency `omega`. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View Solution
All Questions questions and complete solutions for chapter CIRCULAR,ROTATIONAL & SIMPLE HARMONIC MOTION of D MUKHERJEE PHYSICS (HINGLISH) of Class 12