Complete Solutions to Type 1 of chapter KINEMATICS, FORCES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | KINEMATICS, FORCES |
| D MUKHERJEE | Type 1 |
| Number Of Questions | 79 |
| Academic Year | 2023-24 |
A particle has an initial velocity of `3hat(i) + 4 hat(j)` and an acceleration of `0.4 hat(i) + 0.3 hat(j)`. Its speed after `10s ` is :
View SolutionA bird flies for 4 seconds with a velocity of `|t-2|m//sec.` In a straight line, where `t=` time in seconds. It covers a distance of
View SolutionA particle has an initial velocity of `9m//s` due east and a constant acceleration of `2m//s^(2)` due west. The distance coverd by the particle in the fifth second of its motion is :
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss in kinetic energy for any displacement x is proportional to
View SolutionFor a particle moving along a straight line, the displacement x depends on time t as `x = alpha t^(3) +beta t^(2) +gamma t +delta`. The ratio of its initial acceleration to its initial velocity depends
View SolutionA body is thrown vertically upwards from `A`. The top of a tower . It reaches the ground in time `t_(1)`. It it is thrown vertically downwards from `A` with the same speed it reaches the ground in time `t_(2)`, If it is allowed to fall freely from `A`. then the time it takes to reach the ground.
 .
.
View SolutionWater drops fall at regular intervals from a roof. At an instant when a drop is about to leave the roof, the separations between 3 successive drops below the roof are in the ratio
View SolutionThree particles A, B and C are thrown from the top of a tower with the same speed. A is thrown up, B is thrown down and C is horizontally. They hit the ground with speeds `v_(A),v_(B) and v_(C)` respectively then,
View SolutionA balloon starts rising from the ground with an acceleration of `1.25ms^-2`. After 8 seconds, a stone is released from the balloon. After releasing, the stone will:
View SolutionA particle thrown up vertically reaches its highest point in time `t_(1)` and returns to the ground in a further time `t_(2)`. The air resistace exerts a constant force on the particle opposite to its direction of motion.
View SolutionAn aeroplane at a constant speed releases a bomb.As the bomb drops away from the aeroplane,
View SolutionA projectile is moving at `60 m//s` at its highest point, where it breaks into two equal parts due to an internal explosion. One part moves vertically up at `50m//s` with respect to the ground. The other part will move at
View SolutionTwo particles are projected simultaneously in the same vertical plane, from the with speed `u_(1)` and `u_(2)` at angle of projection `theta_(1)` and `theta_(2)` respectively with the horizontal. The path followed by one, as seen by other (as long as both are in flight), is
View SolutionTwo particles are projected simultaneously in the same vertical plane from the same point, with different speeds `u_(1)` and `u_(2)`, making angles `theta_(1)` and `theta_(2)` respectively with the horizontal, such that `u_(1) cos theta_(1) = u_(2) cos theta_(2)`. The path followed by one, as seen by the other (as long as both are in flight), is
View SolutionA stone is thrown with a velocity `v` at an angle `theta` with the horizontal.Its speed when it makes an angle `beta` with the horizontal is
View Solution
A hollow vertical cylinder of radius r and height h has a smooth internal surface. A small particle is placed in contact with the inner side of the upper rim, at point A, and given a horizontal speed u, tangentical t the rim. it leaves the lower rim at point B, vertically below A. If n is an integer then
View SolutionA light particle moving horizontally with a speed of `12 m//s` strikes a very heavy block moving in the same direction at `10 m//s`. The collision is one-dimensional and elastic. After the collision, the particle will
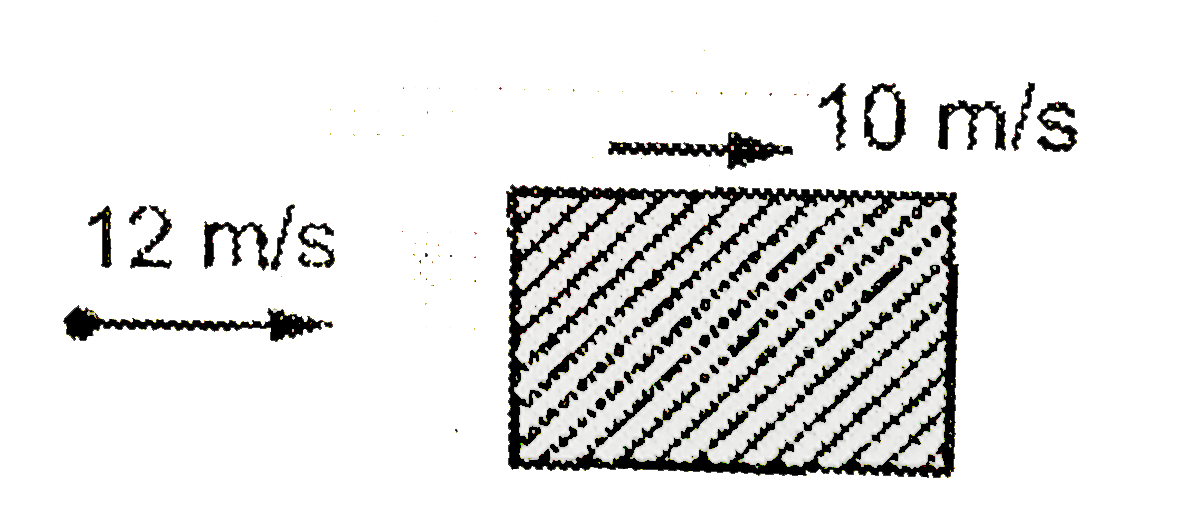
View SolutionA ball falls vertically onto a floor with momentum `p`, and then bounces repeatedly. If the coefficient of restitution is `e`, then the total momentum imparted by the ball on the floor till the ball comes to rest is
View SolutionA ball falls from rest from a height h onto a floor, and rebounds to a height `h//4`. The coefficient of restitution between the ball and the floor is
View SolutionA particle of mass m moving with velocity u makes an elastic one-dimentional collision with a stationary particle of mass `m`. They come in contact for a very small time `t_0`. Their force of interaction increases from zero to `F_0` linearly in time `0.5t_0`, and decreases linearly to zero in further time `0.5t_0` as shown in figure. The magnitude of `F_0` is
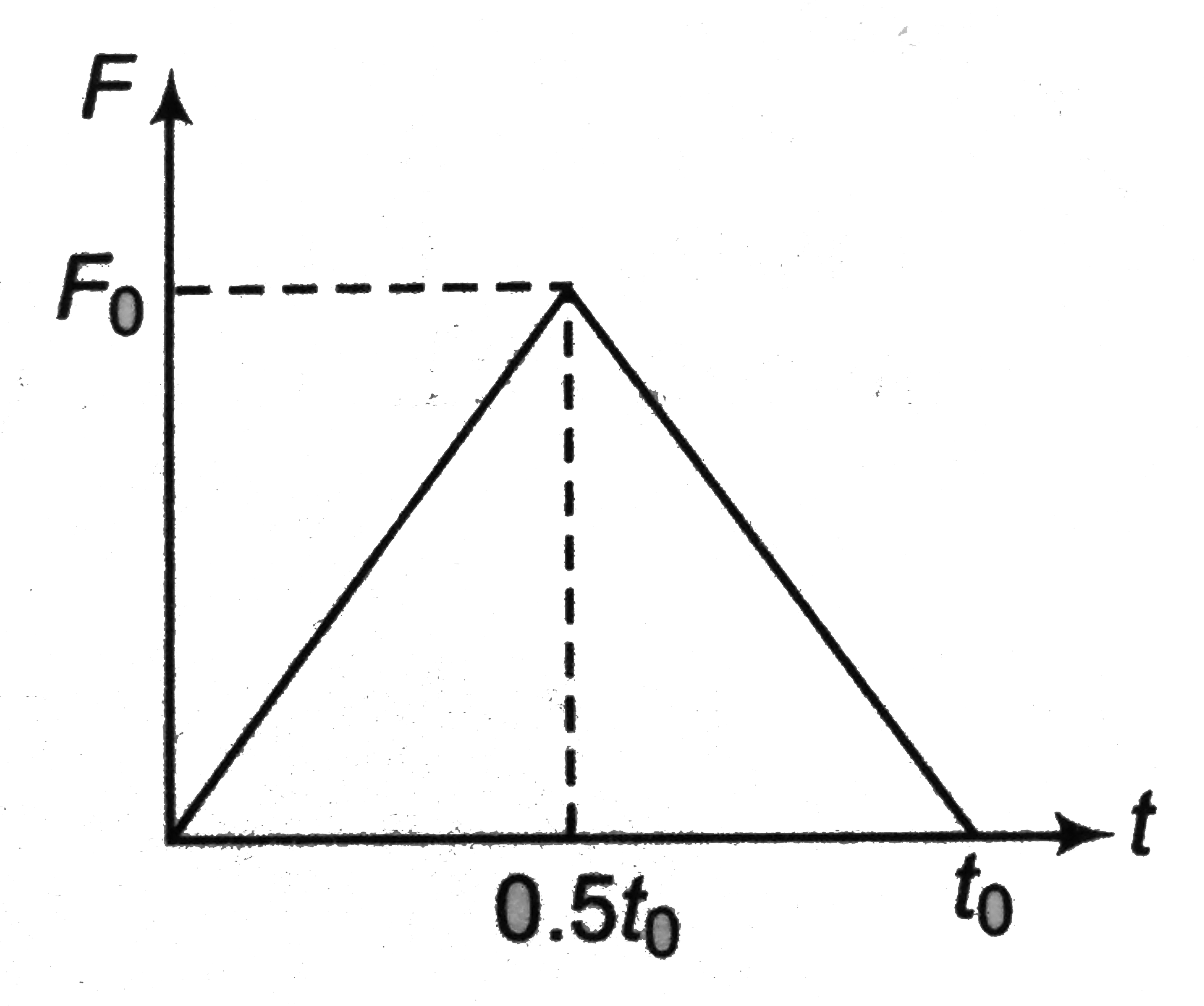
View SolutionA particle of mass `m` , initially at rest , is acted upon by a variable force `F` for a brief interval of time `T`. It begins to move with a velocity `u` after the force stops acting . `F` is shown in the graph as a function of time. The curve is a semicircle.

View SolutionTwo identical spheres move in opposite directions with speeds `v_(1)` and `v_(2)` and pass behind an opaque screen, where they may either cross without touching (Even 1) or make an elastic hand-on collision (Event 2).
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle `theta` to the vertical, and rebounds with a speed `v`, at an angle `phi` to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
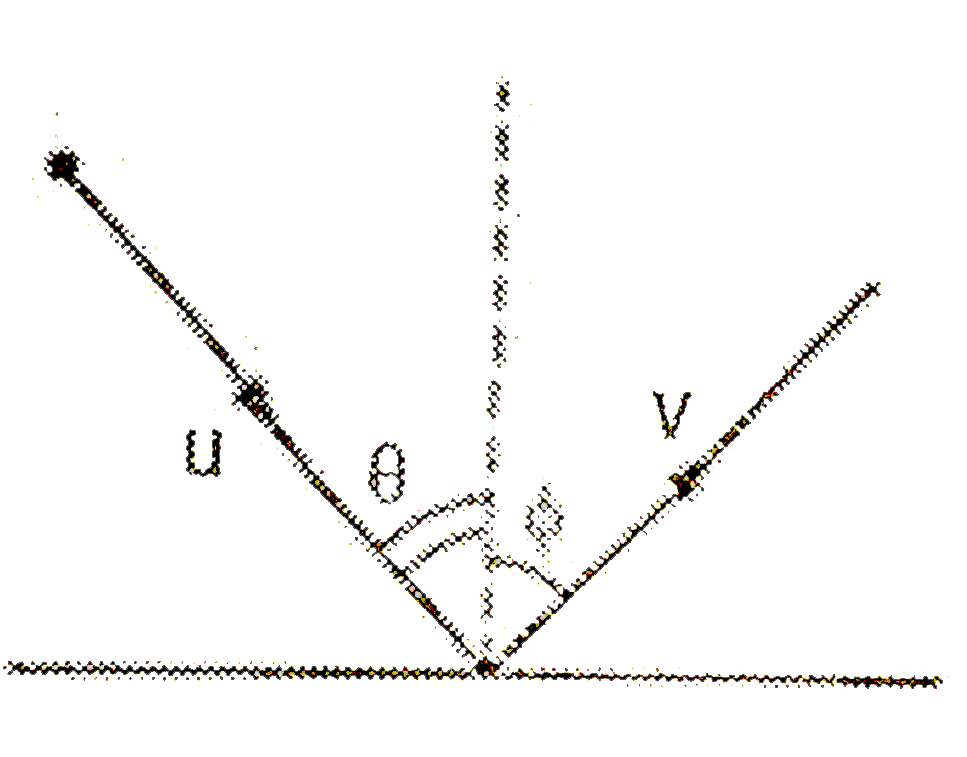
View SolutionIn the previous question the angle `phi` is equal to
View SolutionA particle of mass `m_(1)` makes an elastic, one-dimensional collision with a stationary particle of mass `m_(2)`.What fraction of the kinetic energy of `m_(1)` is carried away by `m_(2)`?
View SolutionA block of mass M is attached to the lower end of a vertical rope of mass m. An upward force P acts on the upper end of the rope. The system is free to move. The force exerted by the rope on the block is `(PM)/(M+m)`
View SolutionBlocks A and B have masses of 2 kg and 3 kg. respectively. The ground is smooth. P is an external force of 10 N. The force exerted by B on A is

View SolutionA man slides down a light rope whose breaking strength is `eta` times his weight (`etalt1`) . What should be his minimum acceleration so that the rope just breaks?
View SolutionA particle of small m is joined to a very heavy body by a light string passing over a light pulley. Both bodies are free to move. The total downward force on the pulley is
View SolutionA uniform chain of mass m hangs from a light pulley, with unequal lengths of the chain hanging from the two sides of the pulley. The force exerted by the moving chain on the pulley is
View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are placed in contact with each other on a horizontal platform. The coefficient of friction between the platform and the two blocks is the same. The platform moves with an acceleration. The force of interaction between the blocks is `:`

View SolutionIn the figure, the blocks A,B and C of mass m each have accelerations `a_(1),a_(2)` and `a_(3)` respectively. `F_(1)` and `F_(2)` are external forces of magnitude 2mg and mg respectively.

View SolutionIn the figure, the vertical sections of the string are long A is released from rest from the position show.
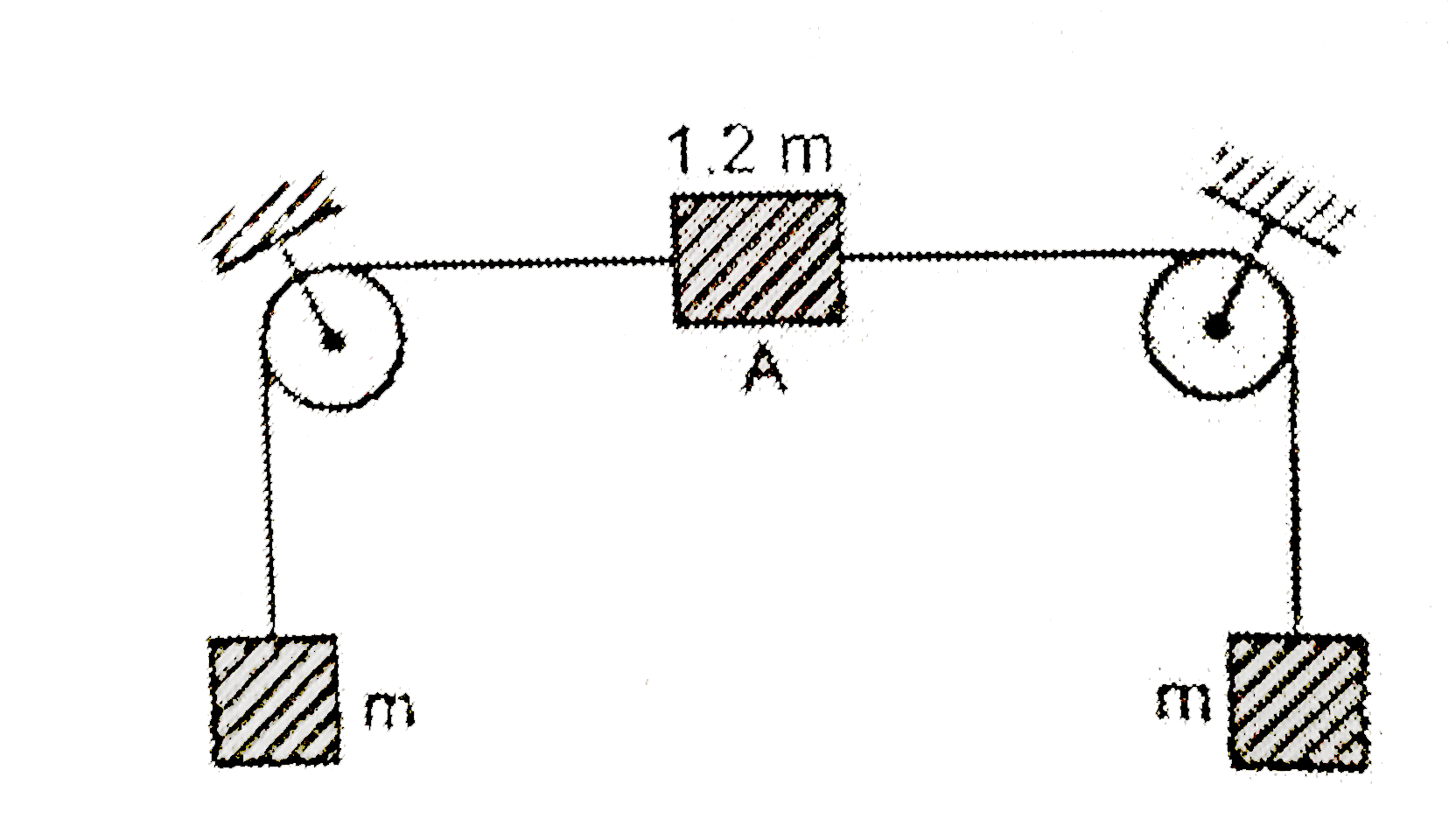
View SolutionA strip of wood of length l is placed on a smooth horizontal surface. An insect starts from one end of the strip, walks with constant velocity and reaches the other end in time `t_(1)`. It then flies off vertically. The strip moves a further distance l in time `t_(2)`.
View SolutionIn a gravity free space, man of mass `M` standing at a height `h` above the floor, throws a ball of mass `m` straight down with a speed `u`. When the ball reaches the floor, the distance of the man above the floor will be.
View Solution
Two persons pull each other through a massless rope in `tug of war` game. Who will win?
View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?

View SolutionIn the arrangement shown, the pulleys are fixed and ideal, the strings are light, `m_(1)gtm_(2)` and S is a spring balance which is itself massless. The readings of S (in units of mass) is
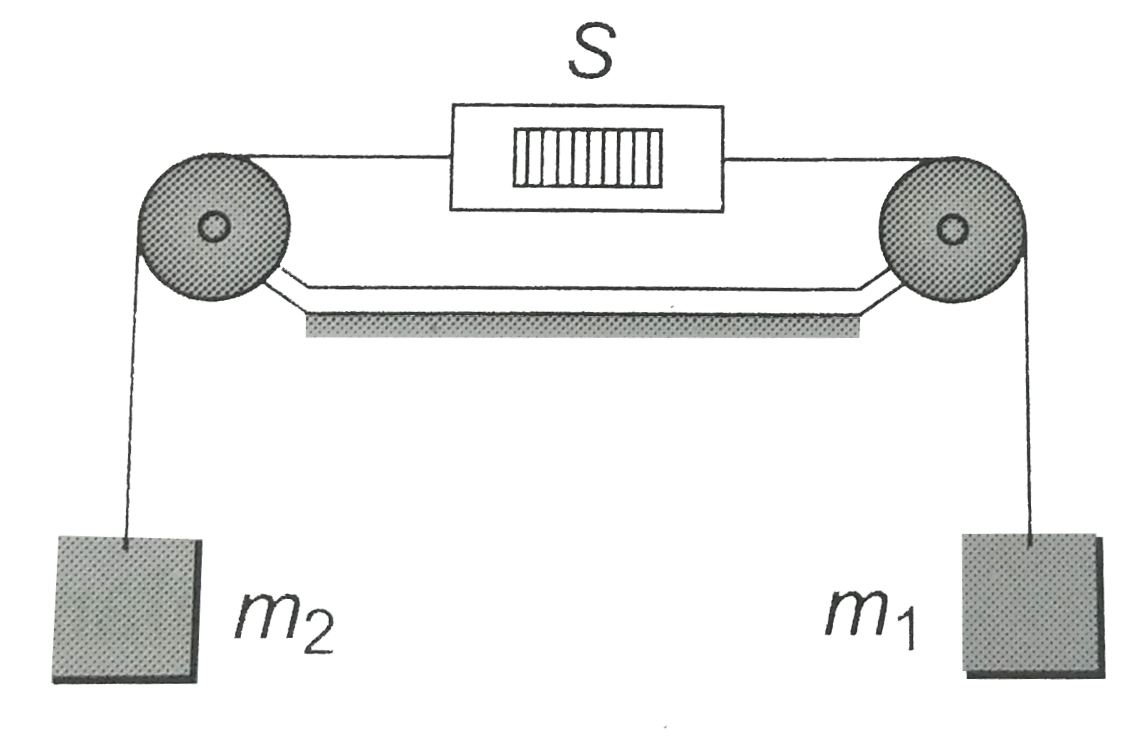
View SolutionBlock A is placed on block B. There is friction between the blocks, while the ground is smooth. A horizontal force P, increasing linearly with time, begins to act on A. The accelerations `a_(1) & a_(2)` of A and B respectively. Are plotted against time (t). Time correct graph is :

View SolutionA bicycle moves on a horizontal road with some acceleration. The forces of friction between the road and the front and rear wheels are `F_(1)` and `F_(2)` respectively.
View SolutionA car starts from rest to cover a distance s. the coefficient of friction between the road and the tyres is `mu`. The minimum time in which the car can cover the distance is proportional to
View SolutionA car starts from rest and moves on a surface in which the coefficient of friction between the road and the tyres increases linearly with distance (x). The car moves with the maximum possible acceleration. The kinetic energy (E) of the car will depend on x as
View SolutionA particle falls from rest under gravity. Its potential energy with respect to the ground (PE) and its kinetic energy (KE) are plotted against time (t). Choose the correct graph.
View SolutionIn the figure, block A is released from rest when the spring is its natural length for the block B of mass m to leave contact with the ground at some stage what should be the minimum mass of block A?
 .
.
View SolutionA force `F=-K(yhati+xhatj)` (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point `(a, 0)`, and then parallel to the y-axis to the point `(a, a)`. The total work done by the force F on the particle is
View SolutionA block of mass `m` is pushed towards a movable wedge of mass `nm` and height `h`, with a velocity `u`. All surfaces are smooth. The minimum value of `u` for which the block will reach the top of the wedge is
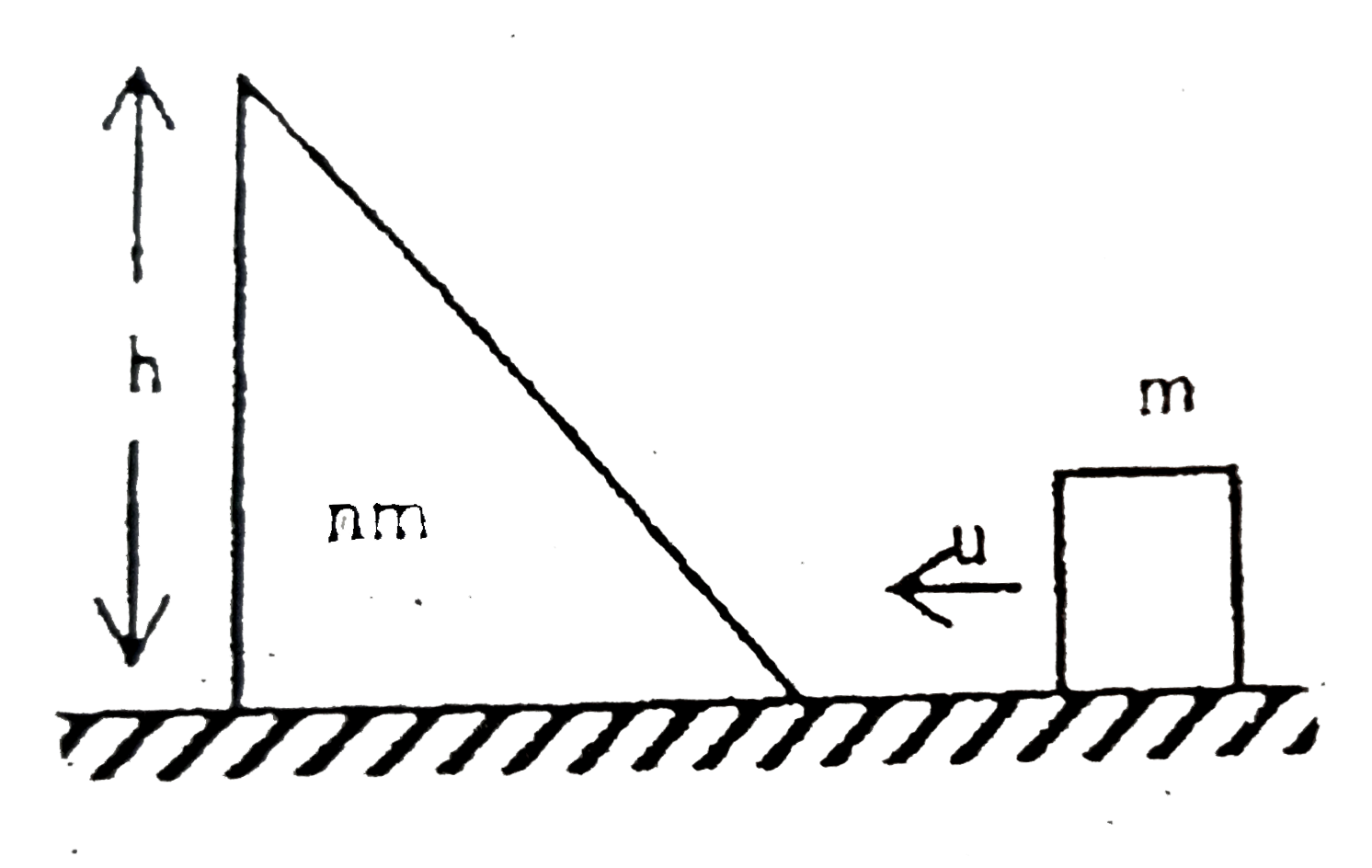
View SolutionA uniform chain of length `l` is placed on rough table with length `l//n` (where `n gt 1`) , hanging over the edge. If the chain just begins to slide off the table by itself from this position, the coefficient of friction between the chain and the table is
View SolutionA chain is held on a frictionless table with L/4 hanging over. Knowing total mass of the chain is M and total length L, the minimum work required to pull hanging part back to the table is :
View SolutionA spring, which is initially in its unstretched condition, is first stretched by a length x and then again by a further length x. The work done in the first case is `W_(1)` and in the second case is `W_(2)`.
View Solution
The ring R in the arrangement shown can slide along a smooth, fixed, horizontal rod XY. If is attached to the block B by a light sring. The blocks is released from rest, with the string horizontal.
View SolutionA strip of wood of mass M and length l is placed on a smooth horizontal surface. An insect of mass m starts at one end of the strip and walks to the other end in time t, moving with a constant speed.
View SolutionA charged particle X moves directly towards another charged particle Y. For the 'X plus Y' system, the total momentum is p and the total energy is E.
View SolutionIn a one-dimensional collision between two particles, their relative velocity is `vec(v)_(1)` before the collision and `vec(v)_(2)` after the collision.
View SolutionA sphere A moving with a speed u and rotating with an angular velocity `omega`, makes a head-on elastic collision with an identical stationary sphere B. There is no friction between the surfaces of a and B. Disregard gravity.
View SolutionIn an elastic collision between spheres A and B of equal mass but unequal radii, A moves along the x-axis and B is stationary before impact. Which of the following is possible after impact ?
View SolutionIn a one dimensional collision between two identical particles A and B, B is stationary and A has momentum p before impact. During impact, B gives impulse J to A.
View SolutionWhen a cannot sheel explodes in mid-air,
View SolutionA cannot shell is fired to hit a target at a horizontal distance R. However, it breaks into two equal parts at its highest point. One part (A) returns to the cannon. The other part
View SolutionA particle moving with a speed v changes direction by an angle `theta`, without change in speed.
View SolutionA block of weight 9.8N is placed on a table. The table surface exerts an upward force of 10 N on the block. Assume `g = 9.8 m//s^(2)`.
View Solution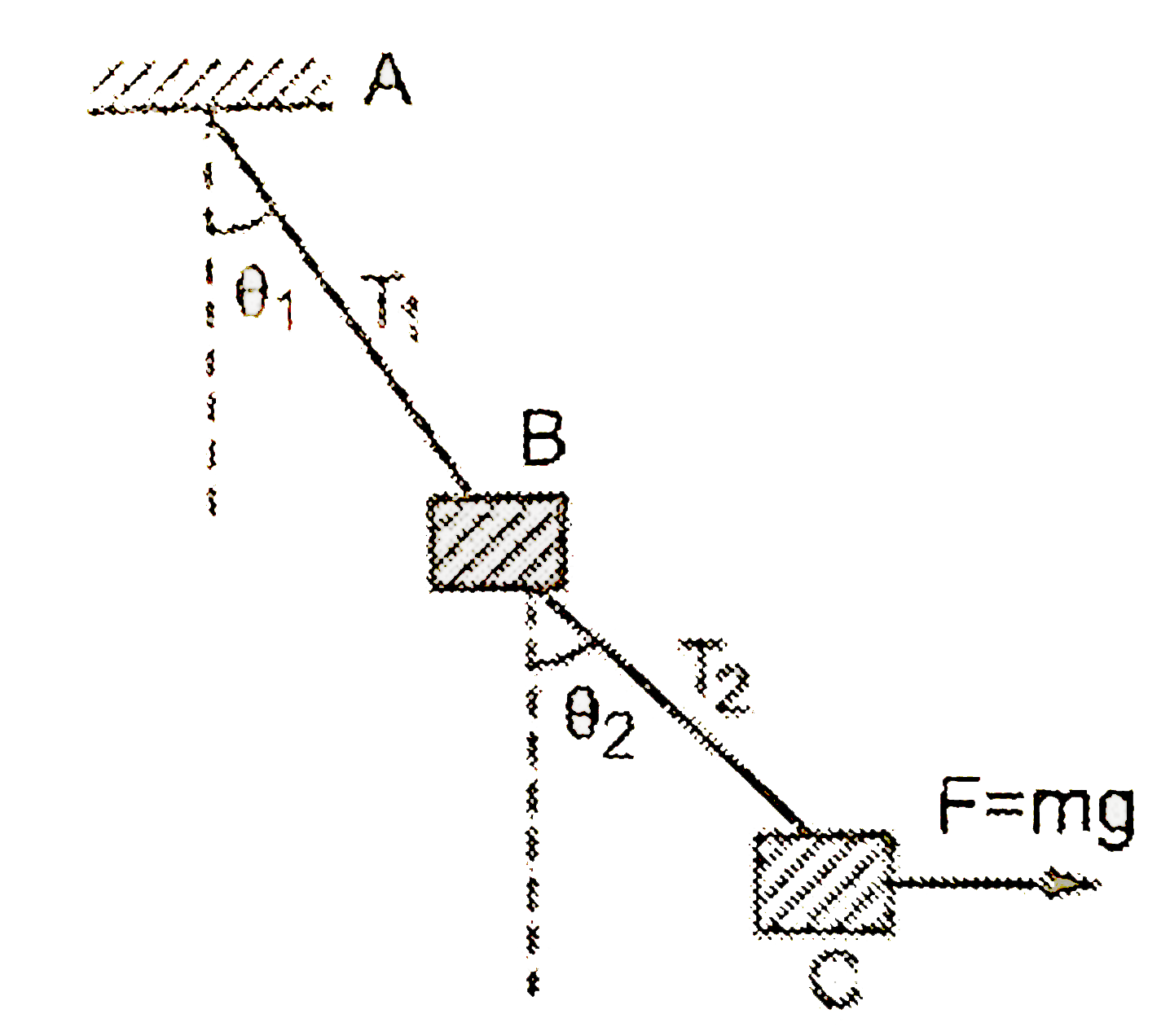
The blocks B and C in the figure have mass m each. The strings AB and BC are light, having tensions `T_(1)` and `T_(2)` respectively. The system is in equilibrium with a constant horizontal force mg acting on C.
View SolutionA particle of mas 70g, moving at `50cm//s`is acted upon by a variable force opposite to its direction of motion. The force F is shown as a function of time t.

View SolutionA monkey of mass mkg slides down a light rope attached to a fixed spring balance, with an acceleration a. The reading of the spring balance is W kg. [g = acceleration due to gravity]
View SolutionA block of weight W is suspended from a spring balance. The lower surface of the block rests on a weighing mechine. The spring balance reads `W_(1)` and the weighing machine reads `W_(2)(W,W_(1),W_(2)` are in the same unit).
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal acceleration a.
View SolutionTwo masses M and `m(M gt m)` are joined by a light string passing over a smooth light pulley.

View SolutionAn ideal massless spring S can compressed `1.0` m in equilibrium by a force of `100 N`. This same spring is placed at the bottom of a friction less inclined plane which makes an angle `theta =30^@` with the horizontal. A `10 kg` mass `m` is released from the rest at top of the inclined plane and is brought to rest momentarily after compressing the spring by `2.0 m.` the distance through which the mass moved before coming to rest is.
View SolutionA block of mass of mass 1 kg moves under the influence of external forces on a rough horizontal surface. At some instant it has a speed of 1m/s due east and an acceleration of `1 m//s^(2)` due north . The force of friction acting on it is F.
View SolutionA long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is `mu`:
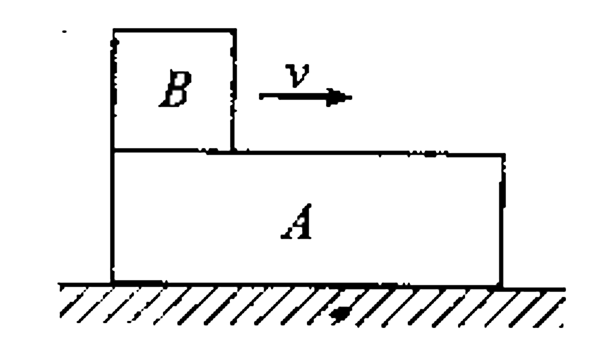
View SolutionA 10-kg block is placed on a horizontal surface. The coefficient of friction between them is `0.2`. A horizontal force P = 15 N first acts on it in the eastward direction. Later, in addition to P a second horizontal force Q = 20 N acts on it in the northward direction.
View SolutionA block of mass m is placed on a rough horizontal surface. The coefficent of friction between them is `mu`. An external horizontal force is applied to the block and its magnitude is gradually increased. The force exerted by the block on the surface is R.
View Solution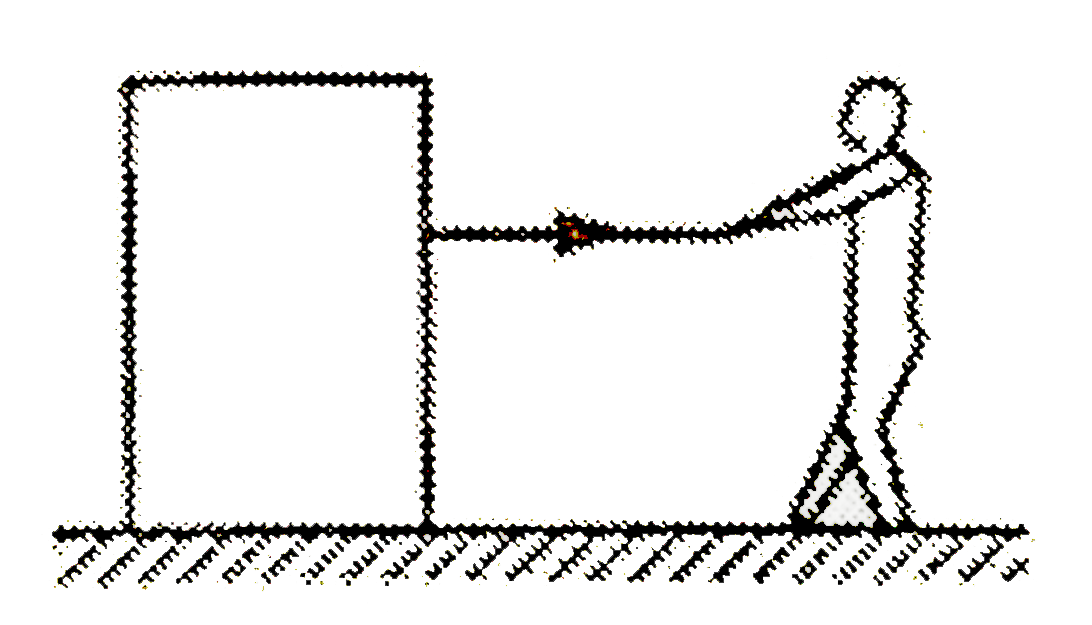 A man pulls a block heavier than himself with a lioght rope. The coefficient if friction is the same between the man and the ground, and between the block and the ground.
A man pulls a block heavier than himself with a lioght rope. The coefficient if friction is the same between the man and the ground, and between the block and the ground.
View SolutionA car of mass `m_(1)` rests on a plank P of mass `m_(2)`. The plank rests on a smooth floor. The string and pulley are ideal. The car starts and moves towards the pulley with acceleration.
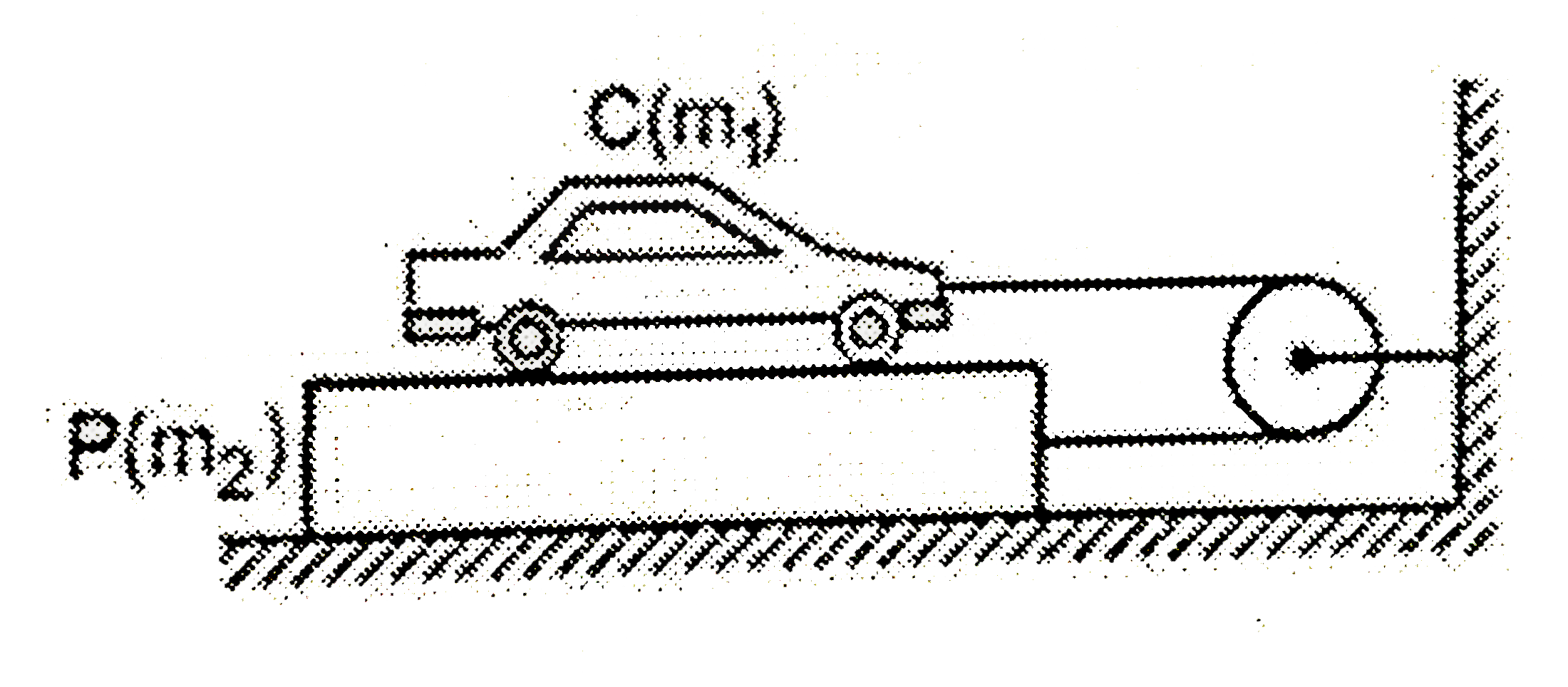
View Solution
A man tries to remain in equilibrium by pushing with his hands and feet against two parallel walls. For equilibrium,
View SolutionTwo men of unequal masses hold on to the two sections of a light rope passing over a smooth light pulley. Which of the following are possible ?
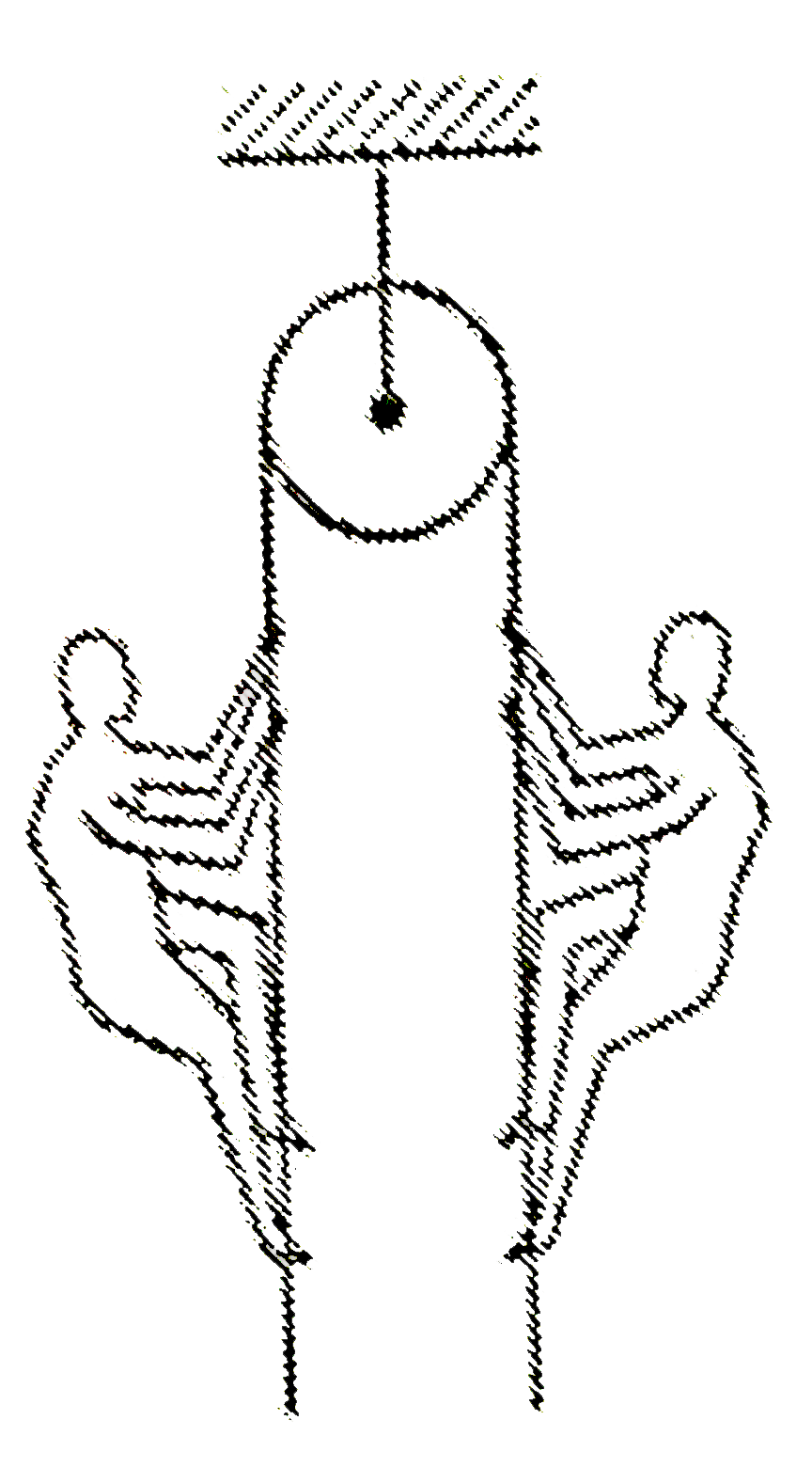
View SolutionInitially both blocks are at rest on a horizontal surface and string is just tight. At t=0, two constant horizontal force `F_(1)` and `F_(2)` start acting on blocks as shown. `f_(1)` and `f_(2)` are frication foces acting on `10 kg` and `20 kg` block (co-efficient of frication between and ground are `0.5`). Values of `F_(1)` and `F_(2)` are given column-I. Then match magnitudes of `f_(1), f_(2)` and direction of `overset(vec)(f_(1))` with corresponding values of `F_(1)` and `F_(2)` given in column-I
`[g = 10 m//s^(2)]`.

View SolutionAn object is given a quick push up an inclined plane. It slides up and then comes back down. It is known that the ratio of the ascent time `(t_("up"))` to the descent time `(t_("dawn"))` is equal to the coefficient of kinetic friction `(mu)`. Find the angle `theta` that the inclined plane makes with the horizontal. Also find the range of `mu` for which the situation described is possible. Assume, that the coefficient of static and kinetic friction are equal.
View SolutionTwo blocks are in contect moving on an inclined plane of inclination `alpha` with the horizontal. The masses of the blocks are equal to `m_(1)` and `m_(2)` and the coefficients of friction between the inclined plane and the blocks are equal to `mu_(1)` and `mu_(2) (mu_(1) gt mu_(2))` respectively. Find (a) common acceleration of the blocks and (b) the contact force between the blocks.

View SolutionA ball of mass `m` is attached to the lower end of a light vertical spring of force constant `K`. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal `(` unstretched `)` length, and comed to rest again after descending through a distance `x`.
View Solution
Type 1 questions and complete solutions for chapter KINEMATICS, FORCES of D MUKHERJEE PHYSICS (HINGLISH) of Class 12