A particle falls from rest under gravity. Its potential energy with respect to the ground (PE) and its kinetic energy (KE) are plotted against time (t). Choose the correct graph.


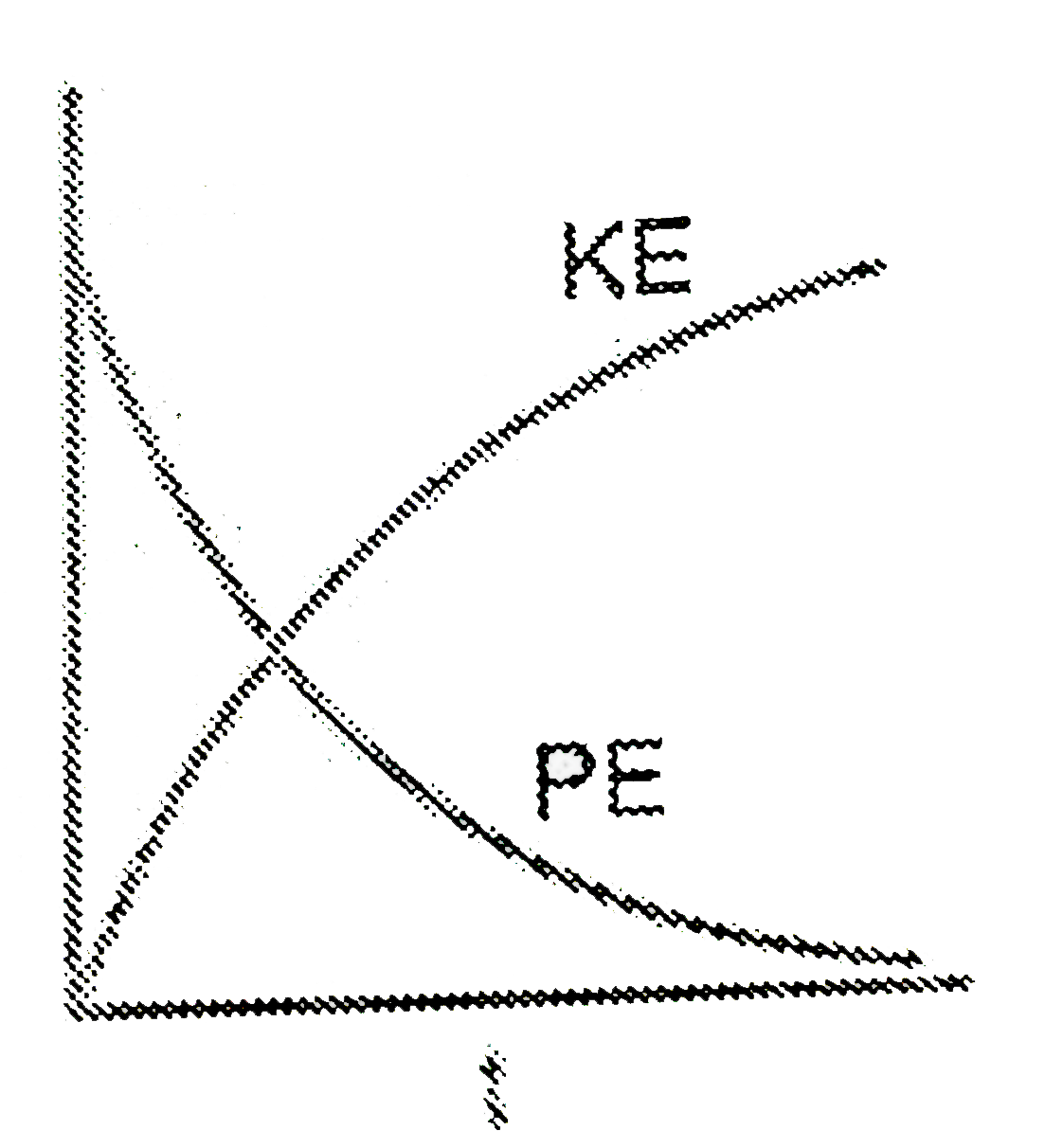
The correct Answer is:B
To solve the problem of determining the correct graph for the potential energy (PE) and kinetic energy (KE) of a particle falling from rest under gravity, we need to analyze how both energies change over time.
1. Understanding the Motion:
- A particle falls from rest under the influence of gravity. Initially, it has zero kinetic energy and maximum potential energy.
2. Potential Energy (PE):
- The potential energy of the particle with respect to the ground can be expressed as:
PE=mgh
where h is the height of the particle above the ground. As the particle falls, h decreases, leading to a decrease in potential energy.
3. Kinetic Energy (KE):
- The kinetic energy of the particle can be expressed as:
KE=12mv2
where v is the velocity of the particle. As the particle falls, its velocity increases, leading to an increase in kinetic energy.
4. Relationship Between PE and Time:
- Since the particle falls under gravity, the height h can be expressed as:
h=12gt2
- Substituting this into the potential energy formula gives:
PE=mg(12gt2)=12mgt2
- This shows that potential energy is proportional to t2 and decreases as the particle falls.
5. Relationship Between KE and Time:
- The velocity v of the particle can be expressed as:
v=gt
- Substituting this into the kinetic energy formula gives:
KE=12m(gt)2=12mg2t2
- This shows that kinetic energy is also proportional to t2 and increases as the particle falls.
6. Graphical Representation:
- As time progresses:
- Potential energy decreases quadratically (downward curve).
- Kinetic energy increases quadratically (upward curve).
- The total mechanical energy (PE + KE) remains constant if we ignore air resistance.
Conclusion:
The correct graph will show:
- A downward-opening parabola for potential energy (PE) as it decreases over time.
- An upward-opening parabola for kinetic energy (KE) as it increases over time.
- A particle falls from rest under the influence of gravity. Initially, it has zero kinetic energy and maximum potential energy.
- The potential energy of the particle with respect to the ground can be expressed as:
PE=mgh
where h is the height of the particle above the ground. As the particle falls, h decreases, leading to a decrease in potential energy.
- The kinetic energy of the particle can be expressed as:
KE=12mv2
where v is the velocity of the particle. As the particle falls, its velocity increases, leading to an increase in kinetic energy.
- Since the particle falls under gravity, the height h can be expressed as:
h=12gt2
- Substituting this into the potential energy formula gives:
PE=mg(12gt2)=12mgt2
- This shows that potential energy is proportional to t2 and decreases as the particle falls.
- The velocity v of the particle can be expressed as:
v=gt
- Substituting this into the kinetic energy formula gives:
KE=12m(gt)2=12mg2t2
- This shows that kinetic energy is also proportional to t2 and increases as the particle falls.
- As time progresses:
- Potential energy decreases quadratically (downward curve).
- Kinetic energy increases quadratically (upward curve).
- The total mechanical energy (PE + KE) remains constant if we ignore air resistance.
The correct graph will show:
- A downward-opening parabola for potential energy (PE) as it decreases over time.
- An upward-opening parabola for kinetic energy (KE) as it increases over time.
Topper's Solved these Questions
- KINEMATICS, FORCESBOOK - D MUKHERJEECHAPTER - KINEMATICS, FORCESEXERCISE - Type 2
22 Videos
- KINEMATICS, FORCESBOOK - D MUKHERJEECHAPTER - KINEMATICS, FORCESEXERCISE - Revision Exercise
26 Videos
- IIT QUESTIONS 5BOOK - D MUKHERJEECHAPTER - IIT QUESTIONS 5EXERCISE - Matrix matching type
2 Videos
- MISCELLANEOUS QUESTION 1BOOK - D MUKHERJEECHAPTER - MISCELLANEOUS QUESTION 1EXERCISE - Miscellaneous Questions-1 (Straight-Objective Type)
54 Videos
Similar Questions
Knowledge Check
Potential energy (PEn) and kinetic energy (KEn) of electron in nth orbit are related as
APEn=KEnBPEn=−2KEnCPEn=2KEnDPEn=KEnA particle is realesed from a height H from ground. At certain height its kinetic energy is three times its gravitational potential energy with respect to ground. Then choose the correct option(s). (Given 'g' is acceleration due to gravity is constant).
AThe height of the particle at that instant is H2BThe height of the particle at that instant is H4CThe speed of the particle at that instant is √3gH2DThe speed of the particle at that instant is √3gH2A block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
A2 FtmB2FtmCFtmDF2t22m
A particle is performing linear S.H.M. at a point A, on the path, its potential energy is three times kinetic energy. At another point B on the same path, its kinetic energy is 3 times the potential energy. The ratio of the potential energy at A to its potential energy at B is
View SolutionAn alpha particle is accelerated from rest through a potential difference of 100 volt. Its final kinetic energy is
View SolutionA particle is performing linear S.H.M. at a point A, on the path, its potential energy is three times kinetic energy. At another point B on the same path, its kinetic energy is 3 times the potential energy. The ratio of the kinetic energy at A to its kinetic at B is
View SolutionA body is projected vertically up. At certain heighth above the ground, the ratio of its potential energy to the kinetic energy is 2:3. At what height above the ground, the ratio of its kinetic energy to the potential energy will be 2 : 3 ?
View SolutionA particle is projected from the ground with a kinetic energy E at an angle of 60° with the horizontal. Its kinetic energy at the highest point of its motion will be
View Solution
