Complete Solutions to Type 2 of chapter PROPERTIES OF MATTER,FLUIDS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | PROPERTIES OF MATTER,FLUIDS |
| D MUKHERJEE | Type 2 |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
A n object is weighed at the North Pole by a beam balance and a spring balance, giving reading of `W_(B)` and `W_(S)` respectively. It is again weighed in the same manner at the equator, giving readings of `W_(B)'` and `W_(S)'` respectively. Assume that the acceleration due to gravity is the same everywhere and that the balances are sensitive.
View SolutionLet `omega` be the angular velocity of the earth's rotation about its axis. Assume that the acceleration due to gravity on the earth's surface has the same value at the equator and the poles. An object weighed by a spring balance gives the same reading at the equator as at a height `h` above the poles `(h lt lt R)`. The value of `h` is
View SolutionUse the assumptions of the previous question. An object weighed by a spring balance at the equator gives the same reading as a taken at a depth d below the earth's surface at a pole `(d lt lt R)`. The value d is
View SolutionA double star is a system of two stars of masses `m` and `2m`, rotating about their centre of mass only under their mutual gravitational attraction. If `r` is the separation between these two stars then their time period of rotation about their centre of mass will be proportional to
View SolutionThree point masses are at the corners of an equilateral traingle of side `r`. Their separations do not change when the system rotates about the centre of the triangle. For this, the time period of rotation must be proportional to
View SolutionFor a planet moving around the sun in an elliptical orbit, which of the following quantities remain constant ?
View SolutionThe escape velocity for a planet is `v_e`. A particle starts from rest at a large distance from the planet, reaches the planet only under gravitational attraction, and passes through a smooth tunnel through its centre. Its speed at the centre of the planet will be
View SolutionThe escape velocity for a planet is `v_(e)`. A particle is projected from its surface with a speed `v`. For this particle to move as a satellite around the planet,
View SolutionIf a satellite orbits as close to the earth's surface as possible,
View SolutionFor a satellite to orbit around the earth, which of the following must be true?
View SolutionA satellite close to the earth is in orbit above the equator with a period of rotation of `1.5` hours. If it is above a point `P` on the equtor at some time, it will be above `P` again after time ...........
View SolutionA satellite is to be geo-stationary, which of the following are essential conditions?
View SolutionTwo small satellies move in a circular orbits around the earth, at disatnce `r` and `(r + dr)` from the centre of the earth. Their time periods of rotation ate `T` and `T + dT (Delta r lt lt r, DeltaT lt lt T)`. Then
View SolutionLet S be an imaginary closed surface enclosing mass m.Let `dvec(S)` be an element of area on S, the direction of `dvec(S)` being outward from S. Let `vec(E)` be the gravitational intensity at `dvec(S)`. We define `phi = phi_(s)vec(E).dvec(S)`, the integration being carried out over the entire surface S.
View SolutionA small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done ( by an external agent) in doing this is
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
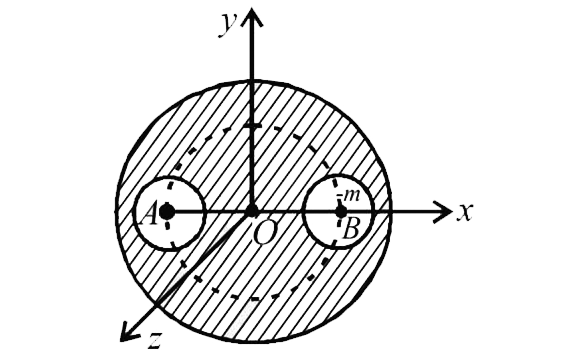
View SolutionThe magnitude of the gravitational field at distance `r_(1)` and `r_(2)` from the centre of a uniform sphere of radius `R` and mass `M` are `F_(1)` and `F_(2)` respectively. Then:
View SolutionAn elastic metal rod will change its length when it
View SolutionThe wires `A` and `B` shown in Fig. are made of the same material and have radii `r_(A)` and `r_(B)`, respectively. The block between them has a mass `m`. When the force `F` is `mg//3`, one of the wires breaks. Then

View SolutionA body of mass `M` is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is `l`.
View SolutionA metal wire of length L, area of cross-section A and young's modulus `Y` is stretched by a variable force `F` such that `F` is always slightly greater than the elastic forces of resistance in the wire. When the elongation of the wire is `l`
View Solutionn drops of a liquid, each with surface energy E. joining to form a single drop
(a). Some energy will be released in the process
(b). Some energy will be absorbed in the process
(c). The energy released or absorbed will be `E(n-n^(2//3))`
(d). the energy released or absorbed will be `nE(2^(2//3)-1)`
View SolutionWhen an air bubble rise from the bottom of a deep lake to a point just below the water surface, the pressure of air inside the bubble
View SolutionWhen a capillary tube is dipped in a liquid, the liquid rises to a height h in the tube. The free liquid surface inside the tube is hemispherical in shape. The tube is now pushed down so that the height of the tube outside the liquid is less than `h`. Then
View SolutionA vertical glass capillary tube, open at both ends, contains some water. Which of the following shapes may not be taken by the water in the tube?
View SolutionA spring balance reads `W_(1)` when a ball is suspended from it. A weighing machine reads `W_(2)` when a tank of liquid is kept on it. When the ball is immersed in the liquid, the spring balance reads `W_(3)` and the weighing machine reads `W_(4)`. Then, which of the following are not correct?
View SolutionIn the previous question,
View Solution_E01_126_Q01.png)
A massless conical flask filled with a liquid is kepth on t a table in a vacuum the force exerted by the liquid on the bse of the flask is `W_(1)`. Th force exerted by the flask on the table is `W_(2)`
View SolutionThe vessel shown in the figure has a two sections of areas of cross-section `A_1` and `A_2`. A liquid of density `rho` fills both th sections, up to a height `h` in each Neglect atmospheric pressure. Choose the wrong option.
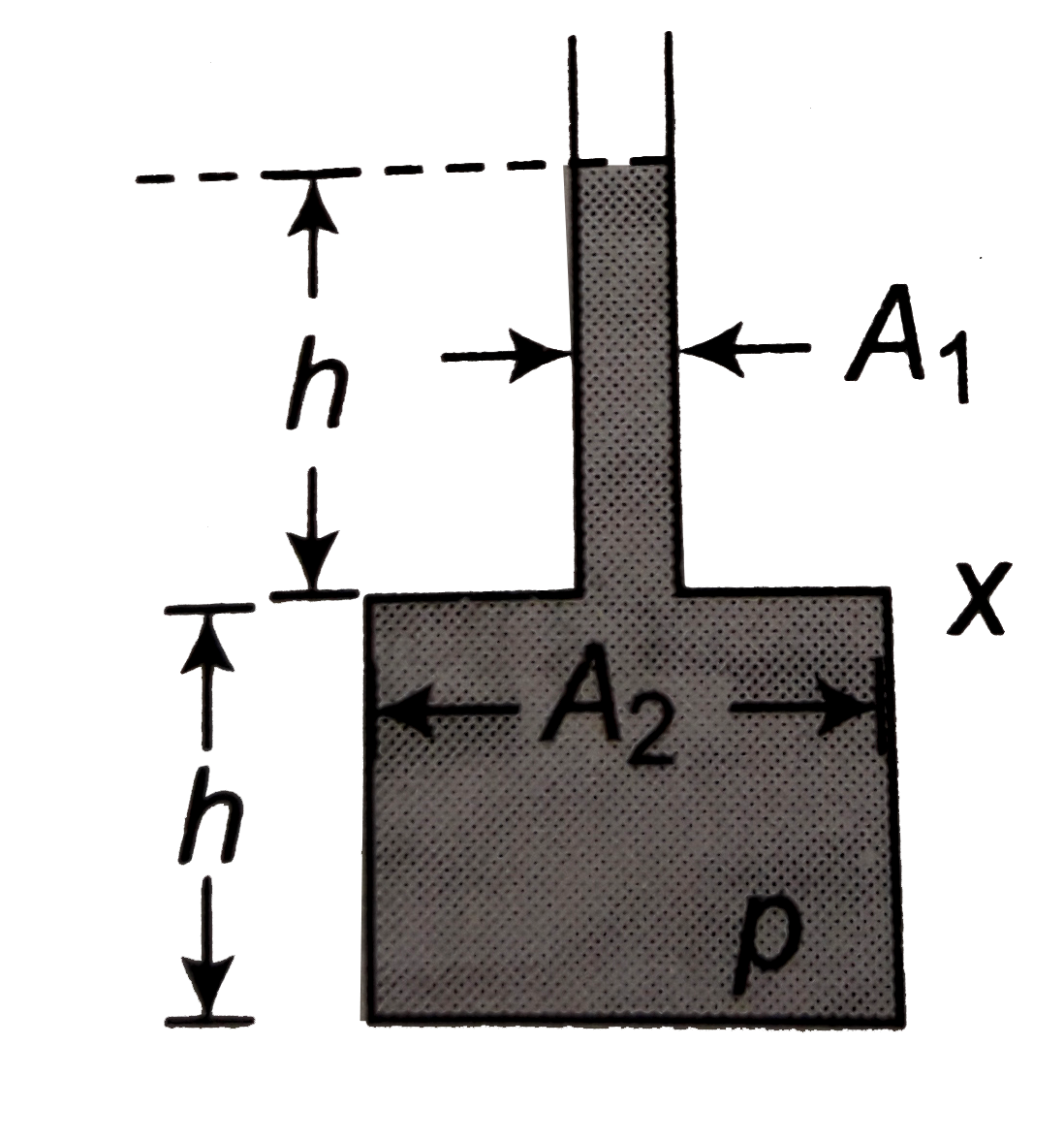 .
.
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
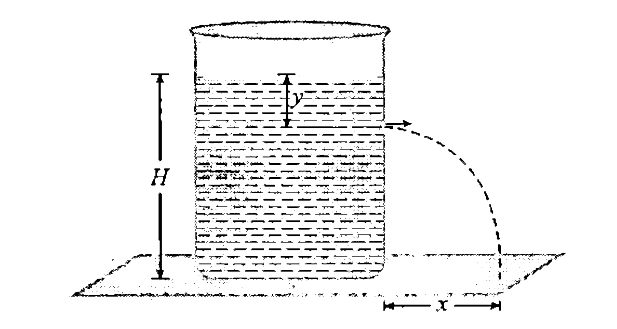
View SolutionIn the figure, an ideal liquid flows through the tube, which is of uniform cross section. The liquid has velocities `v_(A)` and `v_(B)`, and pressures `P_(A)` and `P_(B)` at the points `A` and `B`, respectively. Then
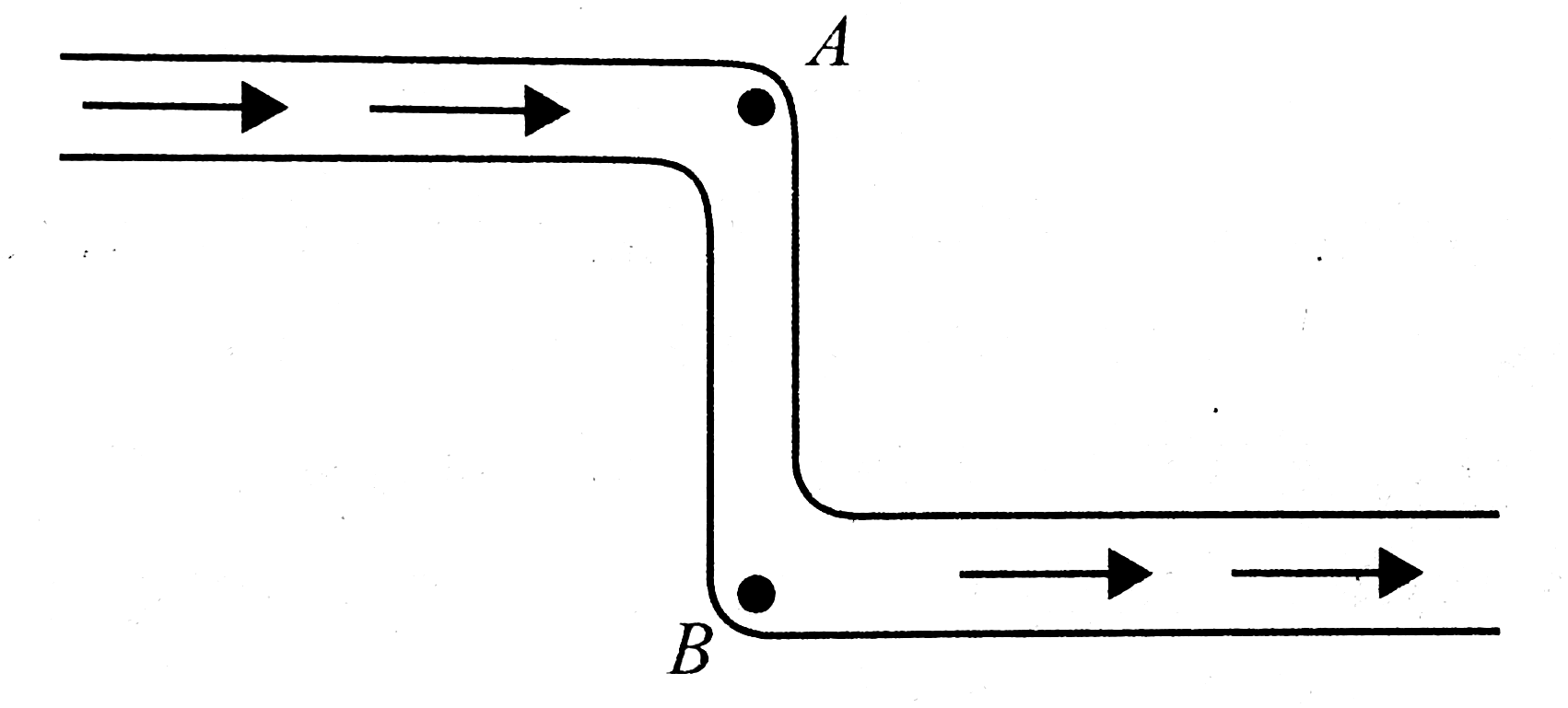
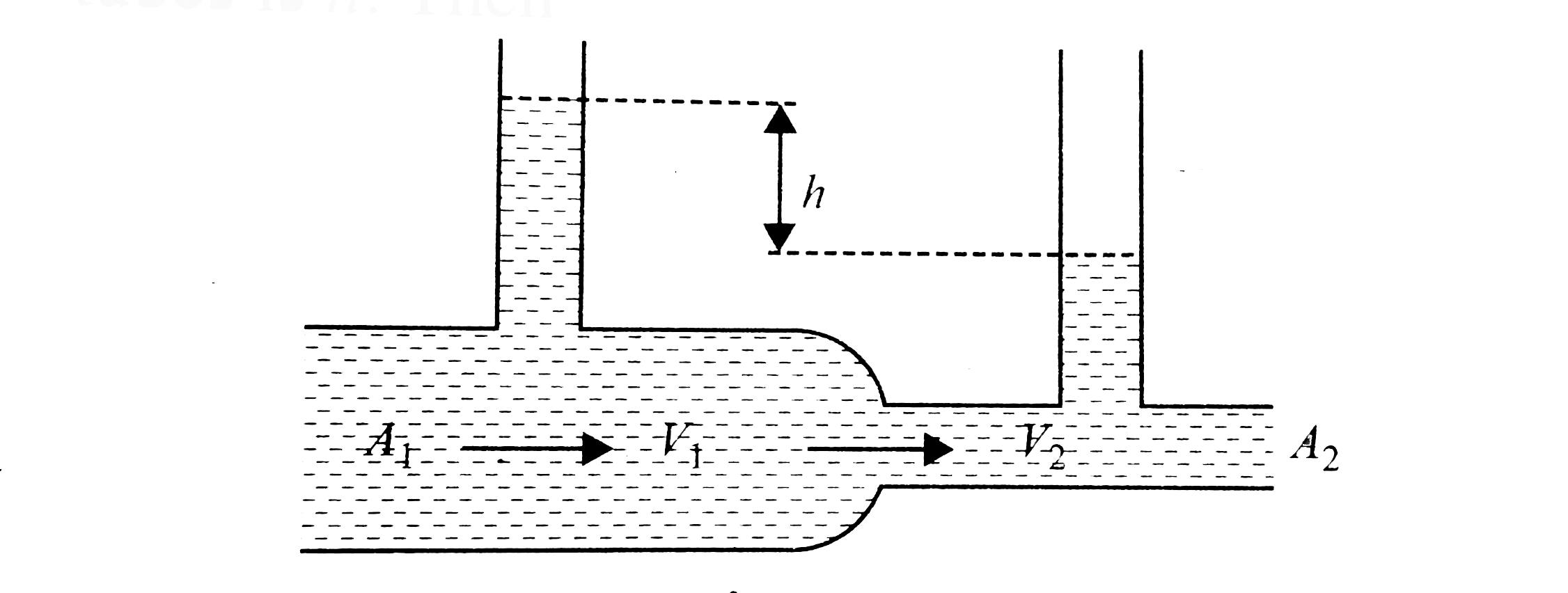
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section `A_(1)` and `A_(2)` are `v_(1)` and `v_(2)` respectively. The difference in the levels of the liquid in the two vertical tubes is `h`. Then
View SolutionA liquid of density `rho` comes out with a velocity `v` from a horizontal tube of area of cross-section `A`. The reaction force exerted by the liquid on the tube is `F`. Choose the incorrect option.
View SolutionA rectangular block of mass `m` and area of cross-section `A` floats in a liquid of density `rho`. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period `T`.
(i) `T prop sqrt(m)`
(ii) `T prop sqrt(rho)`
(iii) `T prop (1)/(sqrt(A))`
(iv) `T prop (1)/(sqrt(rho))`.
View SolutionA vertical `U-tube` contains a liquid. The total length of the liquid column inside the tube is `1`. When the liquid is in equilibrium, the liquid surface in one of the arms of the `U-tube` is pushed down slightly and released. The entire liquid column will undergo a periodic motion.
View Solution
Type 2 questions and complete solutions for chapter PROPERTIES OF MATTER,FLUIDS of D MUKHERJEE PHYSICS (HINGLISH) of Class 12