Complete Solutions to Type 1 of chapter PROPERTIES OF MATTER,FLUIDS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | PROPERTIES OF MATTER,FLUIDS |
| D MUKHERJEE | Type 1 |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
The rotation of the earth about its axis speeds up such that a man on the equator becomes weightless. In such a situation, what would be the duration of one day ?
View SolutionTwo identical trains `A` and `B` move with equal speeds on parallel tracks along the equator. A moves from east to west and `B` moves from west to east. Which train will exert greater force on the track?
View SolutionA small body of superdense material, whose mass is twice the mass of the earth but whose size is very small compared to the size of the earth, starts form rest at a height `H lt lt R` above the earth's surface, and reaches the earth's surface in time `t`. then `t` is equal to
View SolutionThe time period of a simple pendulum of infinte length is
View SolutionThe height of the point vertically above the earth's surface, at which acceleration due to gravtiy becomes 1% of its value at the surface is (Radius of the earth =R)
View SolutionAt what height above the earth's surface is the acceleration due to gravity 1% less than its value at the surface ? [R = 6400 km]
View SolutionLet the acceleration due to gravity be `g_(1)` at a height `h` above the earth's surface `g_(2)` at a depth `d` below the earth's surface. If `g_(1)=g_(2),h lt lt R` and `d lt lt R` then
View SolutionIf different planets have the same density but diferent radii then the acceleration due to gravity (g) on the surface of the planet will depend on its radius (R) as
View SolutionP is a point at a distance r from the centre of a spherical shell of mass M and radius a, where `r lt a`. The gravitational potential at P is
View SolutionA particle of mass m is placed inside a spherical shell, away from its centre. The mass of the shell is M.
View SolutionP is a point at a distance r from the centre of a solid sphere of radius a. The gravitational potential at P is V. IF V is plotted as a function of r, which is the correct curve ?
View SolutionA point `P` lies on the axis of a fixed ring of mass `M` and radius `a`, at a distance `a` from its centre `C`. A small particle starts from `P` and reaches `C` under gravitational attraction only. Its speed at `C` will be.
View SolutionThe escape velocity for a planet is `v_(e)`. A tunnel is dug along a diameter of the planet and a small body is dropped into it at the surface. When the body reaches the centre of the planet, its speed will be
View SolutionIf a small part separates from an orbiting satellite, the part will
View SolutionA satellite going round the earth in a circular orbit loses some energy due to a collision. Its speed is `upsilon` and distance from the earth is d.
View SolutionThe distance of two satellites from the surface of the earth `R` and `7R`. There time periods of rotation are in the ratio
View SolutionInside a satellite orbiting very close to the earth's surface, water does not fall out of a glass when it is inverted. Which of the following is the best explanation for this ?
View SolutionIf a metal wire is stretched a little beyond its elastic limit (or yield point), and released, it will
View SolutionA metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
View SolutionOne end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
View SolutionA cord of mass m length L, area of cross section A and Young's modulus y is hanging from a ceiling with the help of a rigid support. The elogation developed in the wire due to its own weight is
View SolutionA liquid drop at temperature t, isolated from its surroundings, breaks into a number of droplets. The temperature of the droplets will be
View SolutionTwo vertical parallel glass plates are partially submerged in water. The distance between the plates is d and the length is `l`. Assume that the water between the plates does not reach the upper edges of the plates and the wetting is complete. The water will rise to height (`rho=` density of water and `alpha =` surface tension of water)
View SolutionProve that if two bubbles of radii `r_(1)` and `r_(2)(r_(1)ltr_(2))` come in contact with each other then the radius of curvature of the common surface `r=(r_(1)r_(2))/(r_(2)-r_(1))`
View Solution
The value V in the bent tube is initially kept closed. Two soap bubbles A (smaller) and B (larger) are formed at the two open ends of the tube. V is now opened, and air can flow freely between the bubbles.
View SolutionA liquid of density `rho` and coefficient of viscosity `eta`, flows with velocity `upsilon` through a tube of diameter D. A quantity `R = (rho upsilon D)/(eta)` determines whether the flow will be streamlined or turbulent. R has the dimension of
View SolutionA piece of wood floats in water kept in a breaker. IF the beaker moves with a vertical acceleration a, the wood will
View SolutionThe weight of a balloon is `W_(1)` when empty and `W_(2)` when filled with air. Both are weighed in air by the same sensitive spring balance and under identical conditions.
View Solution
A sealed tank containing a liquid of density `rho` moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA U-tube containing a liquid moves with a horizontal acceleration a along a direction joining the two vertical limbs. The separation between these limbs is d. The difference in their liquid levels is
View SolutionThe U-tube shown has a uniform cross-section. A liquid is filled in the two arms up to heights `h_(1)` and `h_(2)`, and then the liquid is allowed to move. Neglect viscosity and surface tension. When the levels equalize in the two arms, the liquid will

View SolutionThe tube shown in figure is of uniform cross-section. Liquid flows through it at a constant speed in the direction shown by arrows. Then the liquid exerts on the tube is:
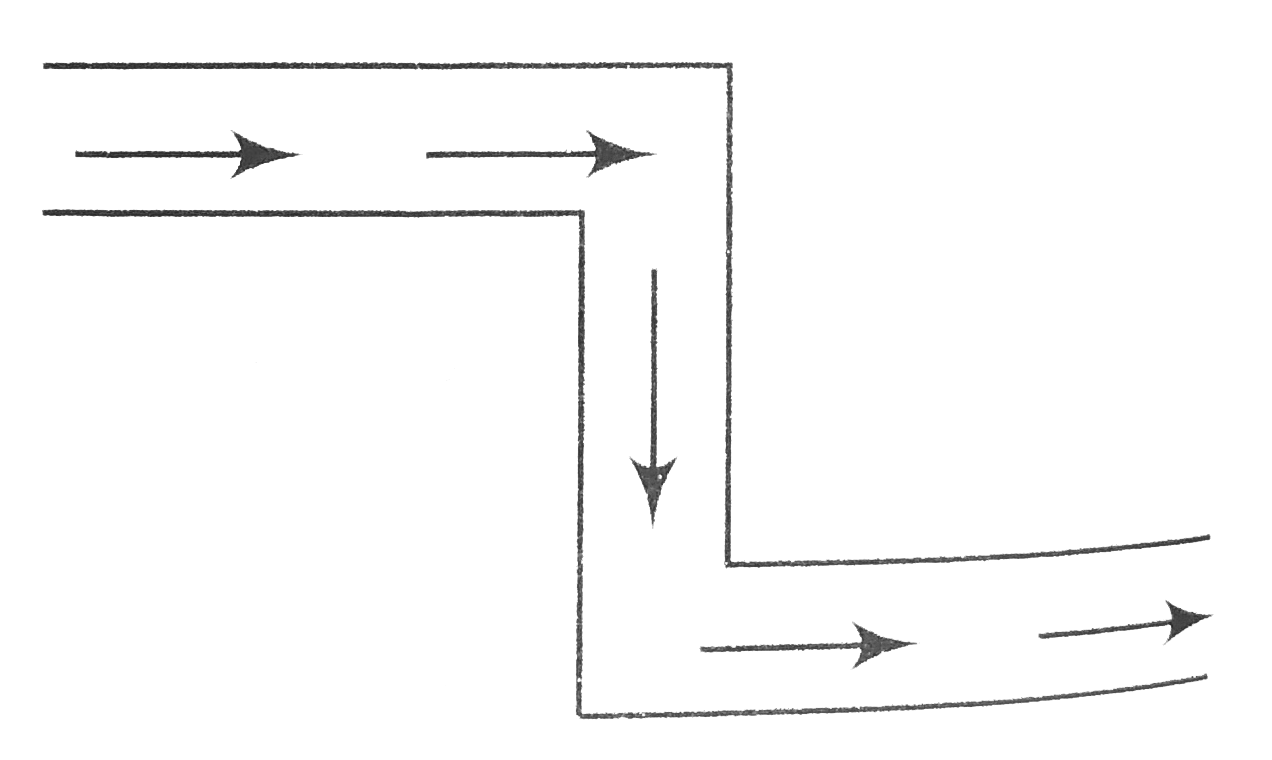
View SolutionBernoulli's principal (or equation) is a consquence of
View Solution_E01_111_Q01.png)
Water coming out of the mouth of a tap and falling vertically in stream line flow forms a tapering column. i.e., the area of cross-section of the liquid column decreases as it moves down which of the following is the most accurate explanation for this-
View SolutionA cylindrical drum, open at the top, contains `30` litres of water. It drains out through a small opening at the bottom. `10` litres of water comes out in time `t_1`, the next `10`litres in a further time `t_2` and the last `10` litres in a further time `t_3` Then,
View SolutionThere are two identical small holes on the opposite sides of a tank containing a liquid. The tank is open at the top. The difference in height between the two holes is `h`. As the liquid comes out of the two holes. The tank will experience a net horizontal force proportional to.
 .
.
View Solution
Type 1 questions and complete solutions for chapter PROPERTIES OF MATTER,FLUIDS of D MUKHERJEE PHYSICS (HINGLISH) of Class 12