Complete Solutions to Example of chapter ELECTROSTATICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| DC PANDEY | Example |
| Number Of Questions | 81 |
| Academic Year | 2023-24 |
How many electrons are there in on coulomb of negative charge?
View SolutionIf we comb our hair on a dry day and bring the comb near small pieces of paper, the comb attracts the pieces, why?
View SolutionDoes the attraction between the comb and the piece of papers last for longer period of time?
View SolutionCan two similarly charged bodies attract each other?
View SolutionDoes centre of mass of a body actually exist in reality? Does centre of mass of a solid body lie necessarily Inside it ?
View SolutionWhy a third hole in a socket provided for grounding?
View SolutionWhat is the smallest electric force between two charges placed at a distance of `1.0m`?
View SolutionThree charges `q_1=1muC, q_2=2muC` and `q_3=3muC` are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge `q_1`

View SolutionTwo identical balls each having a density `rho` are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle `theta` with vertical. Now, both the balls are immersed in a liquid. As a result the angle `theta` does not change. The density of the liquid is `sigma`. Find the dielectric constant of the liquid.
View SolutionAn electric field of `10^5 N//C` points due west at a certain spot. What are the magnitude and direction of the force that acts on a charge of `+2muC and -5muC` at this spot?
View SolutionTwo positive point charges `q_1=16muC` and `q_2=4muC` are separated in vacuum by a distance of `3.0m`. Find the point on the line between the charges where the net electric field is zero.-
View SolutionAs charge `q=1muC` is placed at point `(1m,2m,4m)`. Find the electric field at point `P(0,-4m,3m)`
View SolutionA uniform electric field `E_0` is directed along positive y-driection. Find the change in electric potential energy of a positive test charge `q_0` when it is displaced in this field from `y_i=a` to `y_f=2a` along the y-axis.
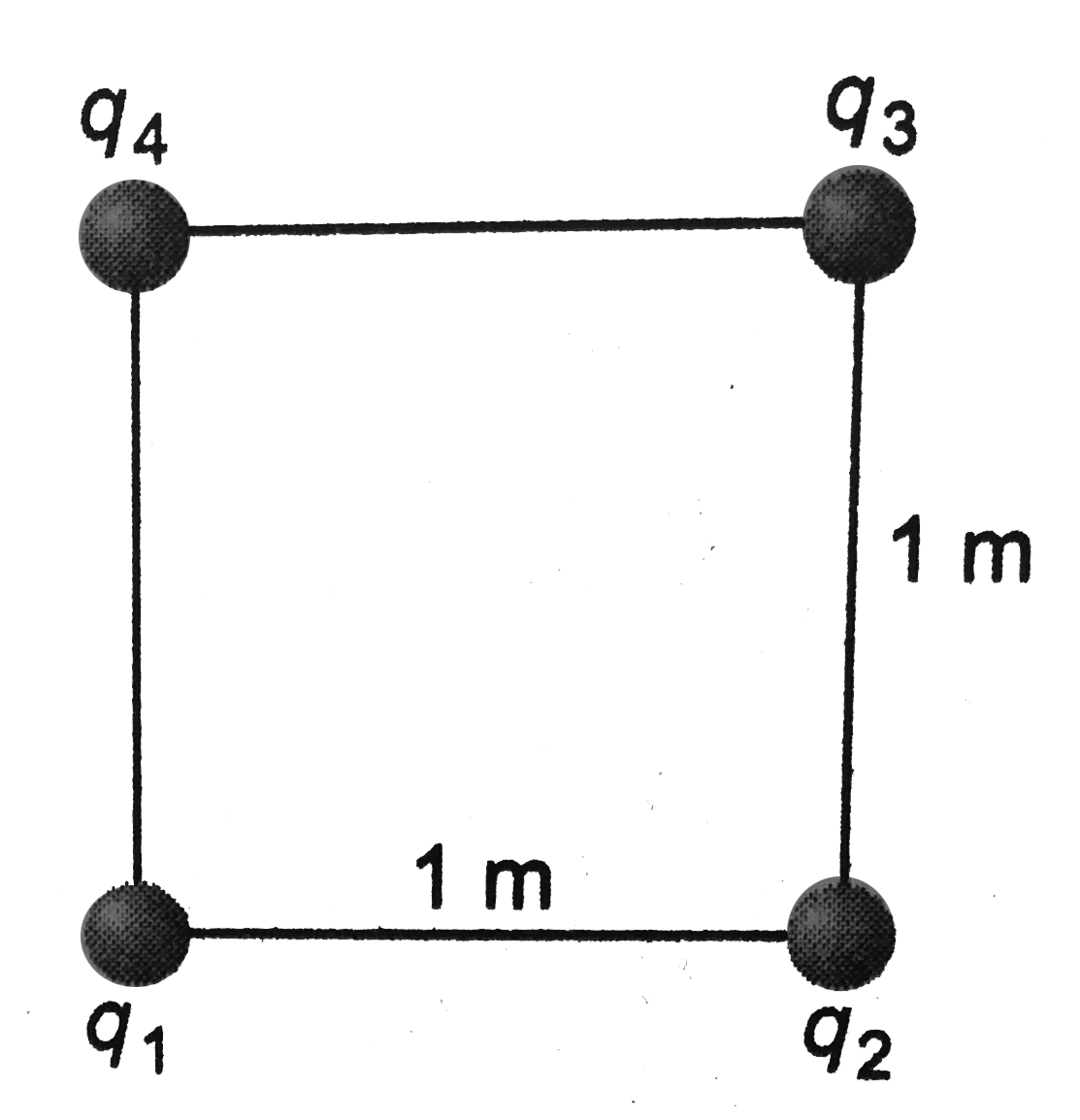
View SolutionFour charges `q_1=1muC, q_2=2muC, q_3=-3muC` and `q_4=4muC` are kept on the vertices of a square of side `1m`. Find the electric potential energy of this system of charges.
View SolutionTwo points charges are located on the x-axis, `q_1=-1muC` at `x=0 and q_2=+1muc` at `x=1m`.
a. Find the work that must be done by an external force to bring a third point charge `q_3=+1muC` from infinity to `x=2m`.
b. Find the total potential energy of the system of three charges.
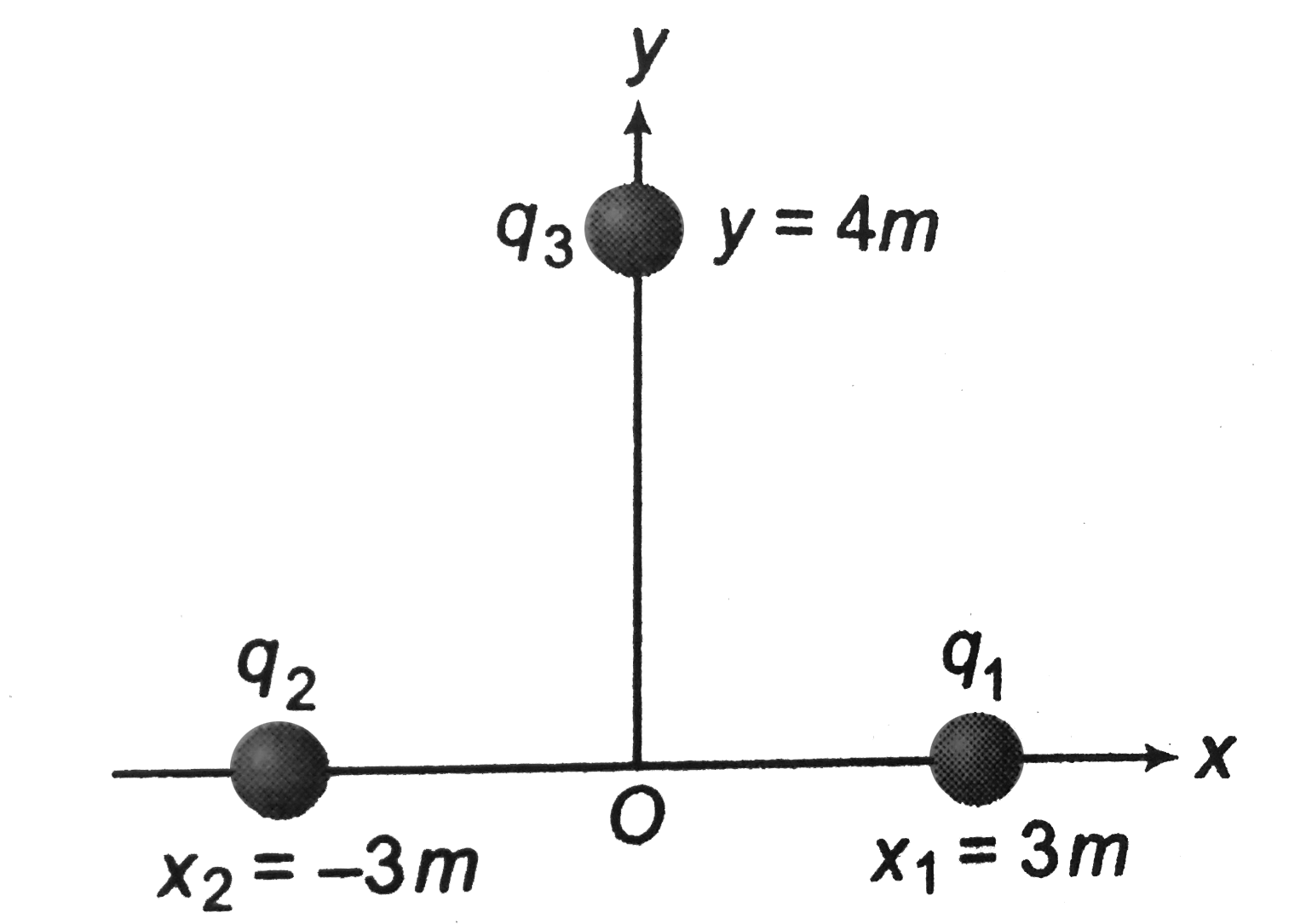
View SolutionTwo point charges `q_1=q_2=2muC` are fixed at `x_1=+3 m` and `x_2=-3m` as shown in figure. A third particle of mass 1 g and charge `q_3=-4muC` is released from rest at `y=4.0m`.Find the speed of the particle as it reaches the origin.
View SolutionThe electric potential at point `A` is `20 V` and at `B` is `-40 V`. Find the work done by an external and electrostatic force in moving an electron slowly from B to A.
View SolutionFind the work done by some external force in moving a charge `q=2muC` from infinity to a point where electric potential is `10^4` V.
View SolutionThree point charge `q_1=1muC, q_2=-2muC` and `q_3=3muC` are placed at `(1m, 0,0), (0,2m,0)` and `(0,0,3m)` respectively. Find the electric potential at the origin.
View SolutionA charge `q=10muC` is distributed uniformly over the circumference of a ring of radius 3m placed on x-y placed with its centre art origin. Find the electric potential at a point `P(0,0,4m)`
View SolutionFind out the points on the line joining two charges `+qand -3q`(kept at as distance of `1.0 m`) where electric potential is zero.
View SolutionThe electric potential in a region is represented a `v = 2x + 3y - z`. Obtain expression for electric field strength.
View SolutionThe electric potential V at any point x,y,z (all in metre) in space is given by `V=4x^2` volt. The electric field at the point `(1m, 0, 2m)` is ……………`V/m`.
View SolutionFind the `V_(ab)` in an electric field `E=(2hati+3hatj+4hatk)N/C`, where `r_a=(hati-2hatj+hatk)m` and `r_b=(2hati+hatj-2hatk)m`
View SolutionIn uniform electric field `E=10 N//C`, find

a. `V_A-V_B` , b. `V_B-V_C`
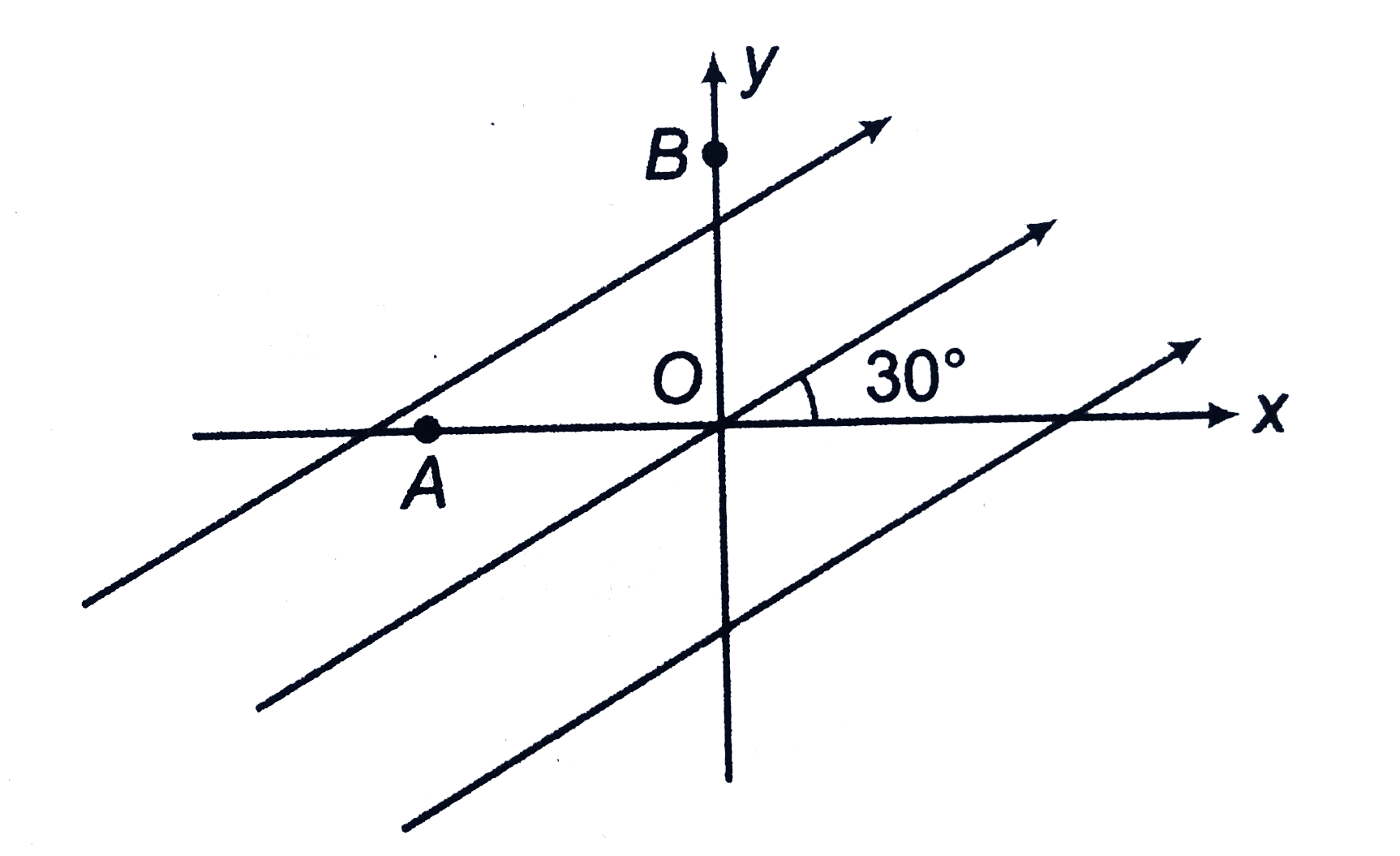
View SolutionA uniform electric field of `100 V//m` is directed at `30^@` with the positive x-axis as shown in figure. Find the potential difference `V_(BA)` if `OA=2`m and `OB=4 m.`
View SolutionA uniform electric field pointing in positive x-direction exists in a region. Let A be the origin, B be the point on the x-axis at `x=+1cm ` and C be the point on the y-axis at `y=+1`cm. then the potetial at the points A,B and C satisfy
a. `V_AltV_B`, b. `V_AgtV_B` c. `V_AltV_C` d. `V_AgtV_C`
View SolutionA non-conducting ring of radius `0.5 m` carries a total charge of `1.11xx10^(-10)`C distributed non-uniformly on its circumference producing an electric field E everywhere in space. The value of the integral `int_(l=oo)^(l=0)-E.dl (l=0` being centre of the ring) in volt is
View SolutionWhat is the total charge of a system containing five charges `+1, + 2, -3, +4` and `-5` in some arbitrary unit?
View SolutionHow many electrons are there in one coulomb of negative charge?
View SolutionA sphere of lead of mass 10 g has net charge `-25 xx 10^(-9)C`.
(i) Find the number of excess electrons on the sphere.
(ii) How many excess electrons are per lead atom ? Atomic number of lead is 82 and its atomic mass is 207 g/mol.
View SolutionA proton and an electron are placed 1.6 cm apart in free speace. Find the magnitude and nature of electrostatic force between them.
View SolutionThe electrostatic force on a small sphere of charege `0.4 muC` due to anther small sphere of charge `-0.8 mu C` in air 0.2 N (i) What is the distance between the two spheres? (ii) What is the force on the second sphere due to the first ?
View SolutionNucleus `._(92)U^(238)` emits `alpha`-particle `(._(2)He^(4))`. `alpha-`particle has atomic number 2 and mass number 4. At any instant `alpha-`particle is at distance of `9 xx 10^(-15)m` from the centre of nucleus of uranium. What is the force on `alpha-`particle at this instant?
`._(92)U^(238) rarr ._(2)He^(4) + ._(90)Th^(234)`
View Solution(a) Two identical sphereshaving positive charges are placed `3 m` apart repel each other with a force `8 xx 10^(-3) N`. Now charges are connected by a metallic wire, they begin to repel each other with a force of `9 xx 10^(-3) N`. Find initial charges on the spheres.
(b) Two identical spheres having charges of opposite signare placed `3 m` apart attract other with a force `2.4 xx 10^(-3) N`. Now spheres are touched and then placed at original separation repel with a force `10^(-3) N`. Find initial charges on the spheres.
View Solution(a) Two protons are placed at some separation in vacuum. Find the ratio of electric and gravitational force acting between them.
(b) Two point charges are placed at separation `3 m` in vacuum. What can be the minimum force between them.
(c ) A charge `Q` is to be divided on two objects. What should be the value of the charges in the objects so that the force between them is maximum ?
(d) Two insulating small spheres are rubbed against each other and placed `1.6 cm` apart. If they attract each other with a force of `0.9 N`, how many electrons were transferred from one sphere to the other during rubbing ?
View SolutionEqual charges each of `20 muC` are placed at `x = 0, 2,4,8,16 cm` on X-axis. Find the force experienced by the charge at `x = 2cm`.
View SolutionFive point charges, each of value +q are placed on five vertices of a regular hexagon of side Lm. What is the magnitude of the force on a point charge of value -q coulomb placed at the centre of the hexagon?
View SolutionThree charges `q_(1) = 1 mu C, q_(2) = -2 muC` and `q_(3) = 3mu C` are placed on the vertices of an equilateral triangle of side 1.0 m. find the net electric force acting on charge `q_(1)`.
How to proceed Charge `q_(2)` will attract charge `q_(1)` (along the line joining them) and charge `q_(3)` will repel charge `q_(1)`. Therefore, two forces will act on `q_(1)`, one due to `q_(2)` and another due to `q_(3)`. Since , the force is a vector quantity both of these force (say `F_(1)` and `F_(2)`) will be added by vector method. Following are two methods of their addition

View SolutionFour charge `Q, q, Q` and q are kept at the four corners of a square as shown below. What is the relation between Q and q, so that the net force on a charge q is zero ?

View SolutionTwo identical helium filled balloons A and B fastened to a weight of 5 g by threads floats in equilibrium as shown in figure. Calculate the charge on each balloons, assuming that they carry equal charge.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is `2theta` in equilibrium.
View SolutionTwo identical balls , each having a charge `q` and mass `m` , are suspended from a common point by two insultating strings each of length `L`. The balls are held at a separation `x` and then released. Find
(a) the electric force on each ball
(b) the component of the resultant force on a ball along and perpendicular to string
(c ) the tension in the string
(d) the acceleration of one of the balls. Consider the situation only for the instant just after the release.
View SolutionTwo identical balls each having a density `rho` are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle `theta` with vertical. Now, both the balls are immersed in a liquid. As a result the angle `theta` does not change. The density of the liquid is `sigma`. Find the dielectric constant of the liquid.
View SolutionAn electric field of `10^5 N//C` points due west at a certain spot. What are the magnitude and direction of the force that acts on a charge of `+2muC and -5muC` at this spot?
View SolutionCalculate the magnitude of the electric field which can just balance a deuteron of mass `3.2xx10^(-27) kg`
View Solutionfind the electric field strength due to a point charge of `5 muC` at a distance of 80 cm from the charge.
View SolutionTwo positive point charges `q_1=16muC` and `q_2=4muC` are separated in vacuum by a distance of `3.0m`. Find the point on the line between the charges where the net electric field is zero.
View SolutionAs charge `q=1muC` is placed at point `(1m,2m,4m)`. Find the electric field at point `P(0,-4m,3m)`
View SolutionA ball having charge `q` and mass `m` is suspended from a string of length `L` between two parallel plates where a vertical electric field `E` is established . Find the time period of simple pendulum if electric field is directed (a) downward and (b) upward.
View SolutionA ball of mass `m` having a charge `q` is released from rest in a region where a horizontal electric field `E` exists.
(a) Find the resultant force acting on the ball.
(b) Find the trajectory followed by the ball.
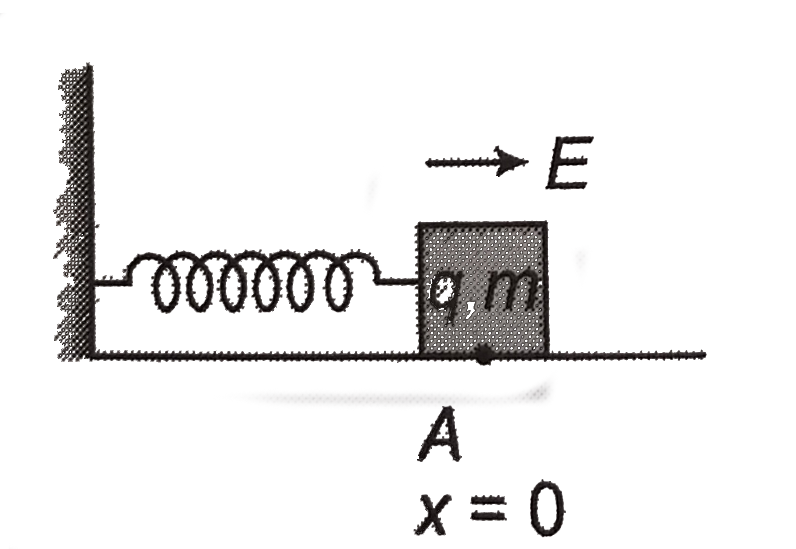
View SolutionA block of mass `m` having charge `q` is attached to a spring of spring constant `k`. This arrangement is placed in uniform electric field `E` on smooth horizontal surface as shown in the figure. Initially spring is unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
View SolutionAn infinite number of charges each equal to q, are placed along the X-axis at `x = 1, x = 2, x = 4, x = 8`,…….. and so on.
(i) find the electric field at a point `x = 0` due to this set up of charges.
(ii) What will be the electric field if the above setup, the consecutive charges have opposite signs.
View SolutionFour charges are placed at the corners of a square of side 10 cm as shown in figure. If q is `1 mu C`, then what will be electric field intensity at the centre of the square?

View SolutionWhat charge would be required to electrify a sphere of radius 25 cm, so as to get a surface charge density of `(3)/(pi)Cm^(-2)`?
View SolutionSixty four spherical drops each of radius `2 cm` and carrying `5 C` charge combine to form a bigger drop. Its capacity is.
View SolutionA charge of `4xx10^(-9)C` is distributed uniformly over the circumference of a conducting ring of radius 0.3m. Calculate the field intensity at a point on the axis of the ring at 0.4m from its centre, and also at the centre.
View SolutionCharges `+- 20nC` are separated by `5mm`. Calculate the magnitude and direction of dipole moment.
View SolutionA system has two charges `q_(A)=2.5xx10^(-7) C` and `q_(B)=-2.5xx10^(-7) C` located at points A, `(0, 0, -0.15 m)` and B, `(0, 0, +0.15 m)` respectively. What is the total charge and electric dipole moment of the system?
View SolutionThree charges are placed as shown . Find dipole moment of the arrangements .
(a)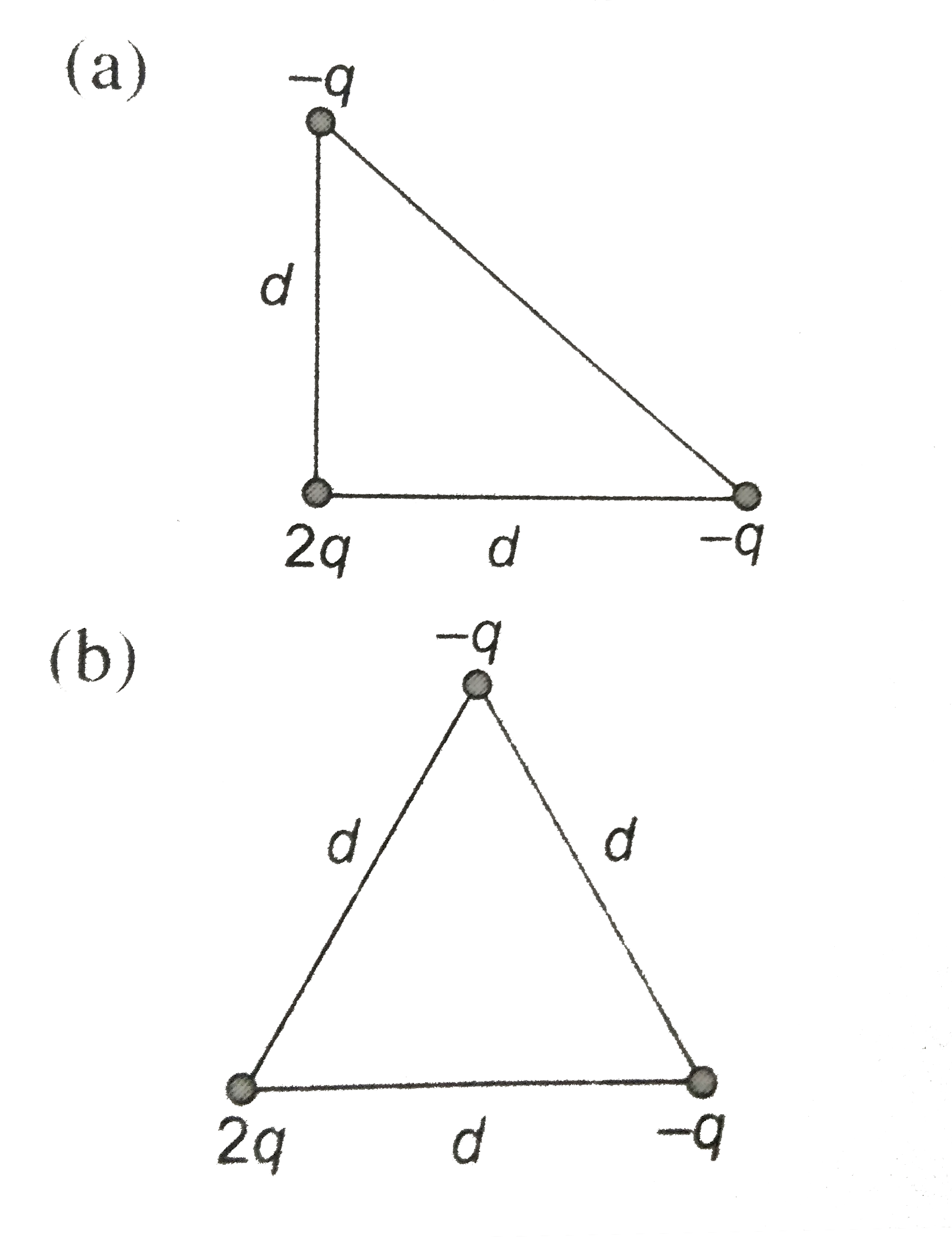
View SolutionTwo opposite charges each of magnitude `2 muC` are 1 cm apart. Find electric field at a distance of 5 cm from the min-point on axid line of the dipole. Also, find the field on equatorial line at the same distance from mid-point
View SolutionWhat is the magnitude of electric intensity due to a dipole of moment `2xx10^(-8)C-m` at a point distant `1 m` from the centre of dipole, when line joining the point to the center of dipole makes an angle of `60^(@)` with dipole axis ?
View SolutionAn electric dipole with dipole moment `4xx10^(-9) C m` is aligned at `30^(@)` with the direction of a uniform electric field of magnitude `5xx10^(4) NC^(-1)`. Calculate the magnitude of the torque acting on the dipole .
View SolutionAn electric dipole of dipole moment `p = 5 xx 10^(-18)C - m` is lying along uniform electric field `E = 4 xx 10^(4) NC^(-1)`. Calculate the work done in rotating the dipole by `60^(@)`.
View SolutionThe electric field in a region is given by `E=ahati+bhatj`. Hence as and b are constants. Find the net flux passing through a square area of side `l` parallel to y-z plane.
View SolutionA rectangular surface of sides `10 cm and 15 cm` is palaced inside a uniform electric field fo `25 Vm^(-1)`, such that normal to the surface makes an angle of `60^(@)` with the direction of electric field. Find the flux of electric field through the rectangular surface.
View SolutionThe electric field in a region is given by `vec (E ) = (E_(0))/(a) x hat(i)`. Find the electric flux passing through a cubical volume bounded by the surfaces `x = 0 , x = a , y = 0 , y = a , z = 0` and `z = a`.
View SolutionA cylinder of radius `R` and length `L` is placed in a uniform electric field `E` parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of `80.0 mu C//m^(2)`. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View SolutionA point charge causes an electric flux of `-1.0xx10^(3) N m^(2)//C` to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface ? (b) What is the is the value of the point charge ?
View SolutionA point charge q is placed at the centre of a cube. What is the flux linked.
a with all the faces of the cube?
b. with each face of the cube?
c. if charge is not at the centre, then what will be the answer of parts a and b ?
View SolutionIf a point charge q is placed at one corner of a cube, what is the flux linked with the cube?
View SolutionA hemispherical body of radius R is placed in a uniform electric field E. What is the flux linked with the curved surface if, the field is (a) parallel to the base, (b) perpendicular to the base.
View SolutionAn infinite line charge produces a field of `9xx10^(4) NC` at a distance of `2cm`. Calculate the linear charge density.
View SolutionA long cylindrical wire carries a positive charge of linear density `lambda`. An electron `(-e ,m)` revolves around it in a circular path under the influence of the attractive electrostatic force. Find the speed of the electron.
View SolutionA large plane sheet of charge having surface charge density `5xx10^(-16) Cm^(-2)` lies in XY plane. Find electric flux through a circular area of radius `1cm`. Given normal to the circular area makes an angle of `60^(@)` with Z-axis.
View SolutionTwo large, thin metal plates are parallel and close to each other. On their faces, the plates have surfaces charge densities of opposite sign and of magnitude `.177 xx 10^(-11)` coulomb per square metre. What is electric field
(i) to the left of the plates ?
(ii) to the right of the plates ?
(iii) in between the plates ?
View SolutionA thin spherical shell of metal has a radius of `0.25 m` and carries charge of `0.2 mu C`. Calculate the electric intensity at `3.0 m` from the centre of the shell.
View SolutionAt a point `20 cm` from the centre of a uniformly charged dielectric sphere of radius `10 cm`, the electric field is `100 V//m`. The electric field at `3 cm` from the centre of the sphere will be
View SolutionTwo non-conducting sphere of radius R have charge Q uniformly distributed. The centres of sphere are `x = 0` and `x = 3R`. Find the magnitude and direction of the net electric field on the X-axis
(i) `x = 0`
(ii) `x = (R)/(2)`
(iii) `x = (3R)/(2)`
(iv) `x = 4R`
View SolutionA non-conducting sphere of radius `R` has a spherical cavity of radius `R//2` as shown. The solid part of the sphere has a uniform volume charge density `rho`. Find the magnitude and direction of electric field at point (a) O and (b) A.

View Solution
Example questions and complete solutions for chapter ELECTROSTATICS of DC PANDEY PHYSICS (HINGLISH) of Class 12
All Exercises from DC PANDEY Class 12 PHYSICS ELECTROSTATICS
- Assertion and Reason
- Check point 1.1
- Check point 1.2
- Check point 1.3
- Check point 1.4
- Check point 1.5
- Example
- Example Type 5
- Example Type 6
- Example Type 8
- Exercise 24.1
- Exercise 24.2
- Exercise 24.3
- Exercise 24.4
- Exercise 24.5
- Exercise 24.6
- Exercise 24.7
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Single Correct
- Match the columns
- Medical entrances gallery
- SUBJECTIVE_TYPE
- Taking it together