Complete Solutions to Taking it together of chapter MAGNETIC FIELD AND FORCES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC FIELD AND FORCES |
| DC PANDEY NEET | Taking it together |
| Number Of Questions | 75 |
| Academic Year | 2023-24 |
Biot-Savart law indicates that the moving electrons (velocity `vecv` ) produce a magnetic field `vecB` such that
View SolutionA current flows in a conductor from east to west. The direction of the magnetic field at a points above the conductor is
View SolutionIn a cyclotron, a charged particle
View SolutionAn electron is projected with uniform velocity along the axis of a current carrying long solenoid. Which of the following is true?
View SolutionA proton is moving along the negative direction of X-axis in a magnetic field directed along the positive direction of Y-axis. The proton will be deflected along the negative direction of
View SolutionLet `[epsilon_(0)]` denote the dimensional formula of the permittivity of the vacuum, and `[mu_(0)]` that of the permeability of the vacuum. If `M = mass ,L = length, T = time and I = electric current`,
View SolutionIn a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.
View SolutionA current `-` carrying circular loop of radius `R` is placed in the `XY-` plane with centre at the origin. Half of the loop with `xgt0` is now bent so that is now lies in the `XY-` plane
View SolutionA particle of charge `q` and mass `m` moves in a circular orbit of radius `r` with angular speed `omega`. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionThe maximum energy of a deuteron coming out a cyclotron is 20 MeV. The maximum energy of proton that can be obtained from this acceleration is
View SolutionA long thin hollow metallic cylinder of radius `'R'` has a current `i` ampere. The magnetic induction `'B'` -away from the axis at a distance `r` from the axis varies as shown in
View SolutionIn hydrogen atom, an electron is revolving in the orbit of radius `0.53 Å` with `6.6xx10^(15) rotations//second`. Magnetic field produced at the centre of the orbit is
View SolutionA particle of charge `q` and velocity v passes undeflected through a space with non-zero electric field E and magnetic field B. The undeflecting conditions will hold, if
View SolutionThe magnetic field at the centre of a circular coil of radius `r` carrying current `l` is `B_(1)`. The field at the centre of another coil of radius `2r` carrying same current `l` is `B_(2)`. The ratio `(B_(1))/(B_(2))` is
View SolutionThree long straight wires `A`, `B` and `C` are carrying current as shown in figure. Then the resultant force on `B` is directed
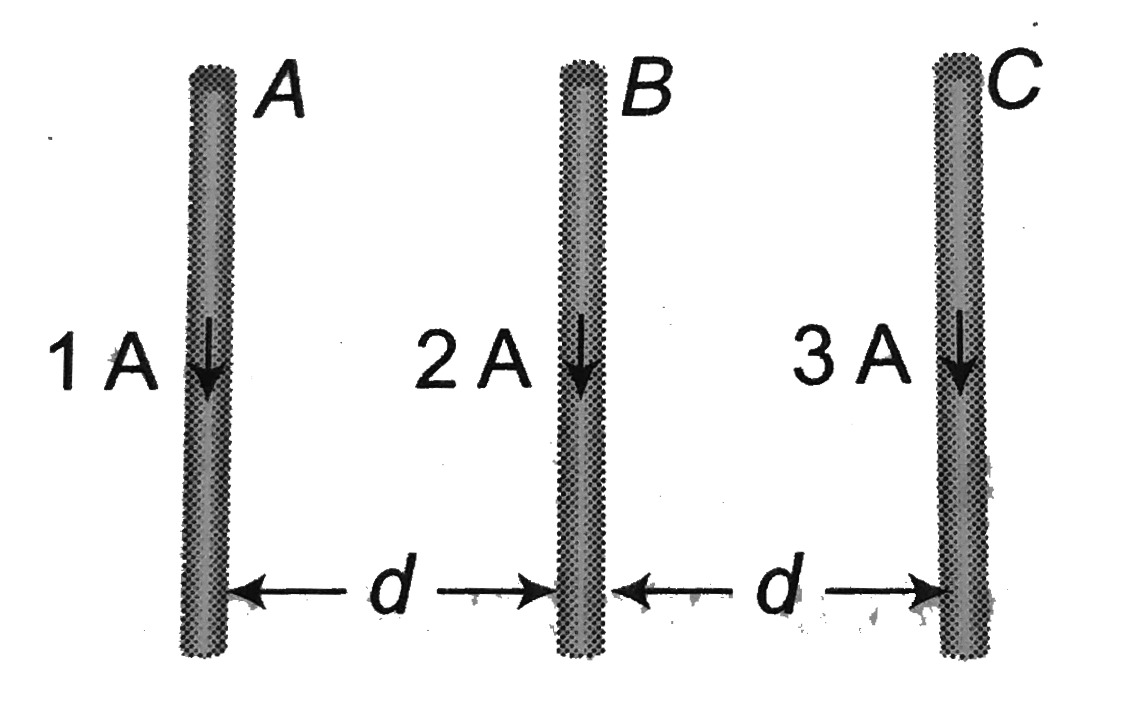
View SolutionA wire of length 2 m carrying a current of 1 A is bend to form a circle. The magnetic moment of the coil is (in `A-m^(2)`)
View SolutionA current carrying conductor of length `l` is bent into two loops one by one. First loop has one turn of wire and the second loop has two turns of wire. Compare the magnetic fields at the centre of the loops
View SolutionTwo charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field `vec(B)=B_(0)hat(K)`
View SolutionWhen a certain length of wire is turned into one circular loop, the magnetic induction at the centre of coil due to some current flowing is `B_(1)` If the same wire is turned into three loops to make a circular coil, the magnetic induction at the center of this coil for the same current will be
View SolutionA long solenoid carrying a current I is placed with its axis vertical as shown in the figure. A particle of mass m and charge q is released from the top of the solenoid. Its acceleration is (g being acceleration due to gravity)
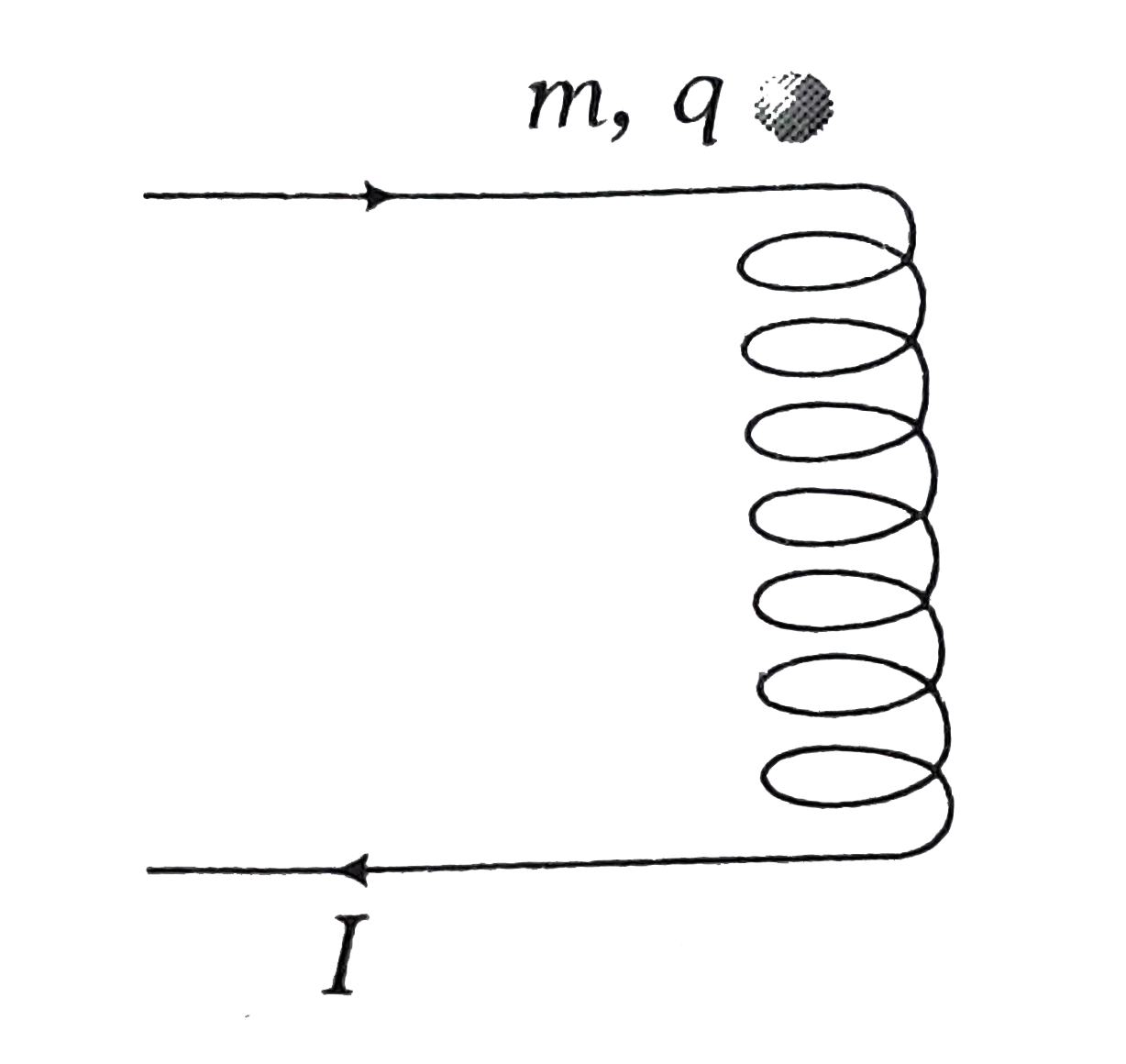
View SolutionA proton moves at a speed `v = 2xx10^(6) m//s` in a region of constant magnetic field of magnitude B = 0.05 T. The direction of the proton when it enters this field is `theta = 30^(@)` to the field. When you look along the direction of the magnetic field, then the path is a circle projected on a plane perpendicular to the magnetic field. How far will the proton move along the direction of B when two projected circles have been completed?
View SolutionAn electric current I enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged paricle q moving along the axis of the circular wire passes through its centre at speed v. The magnetic force acting on the particle when it passes through the centre has a magnitude
View SolutionA particle of mass `m` and charge `q` moves with a constant velocity `v` along the positive `x` direction. It enters a region containing a uniform magnetic field `B` directed along the negative `z` direction, extending from `x = a` to `x = b`. The minimum value of `v` required so that the particle can just enter the region `x gt b` is
View SolutionA proton of mass `1.67xx10^(-27)` kg charge `1.6xx10^(-19) C` is projected in xy-plane with a speed of `2xx10^(6) m//s` at an angle of `60^(@)` to the X-axis. If a uniform magnetic field of 0.14 T is applies along the Y-axis, then the path of the proton is
View SolutionAn equilateral triangle of side length `l` is formed from a piece of wire of uniform resistance. The current `I` is as shown in figure. Find the magnitude of the magnetic field at its centre `O`.

View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R meter. The magnetic induction at the centre of loop is
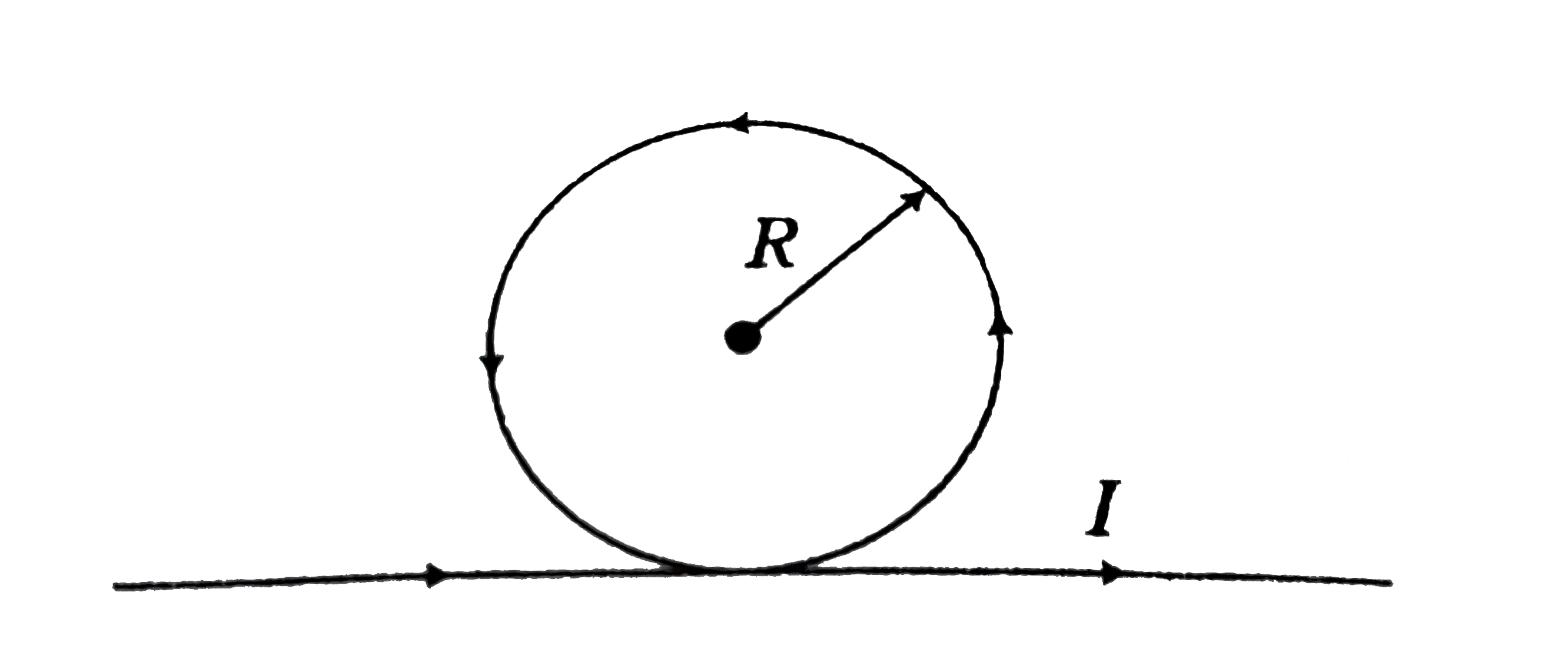
View SolutionMagnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
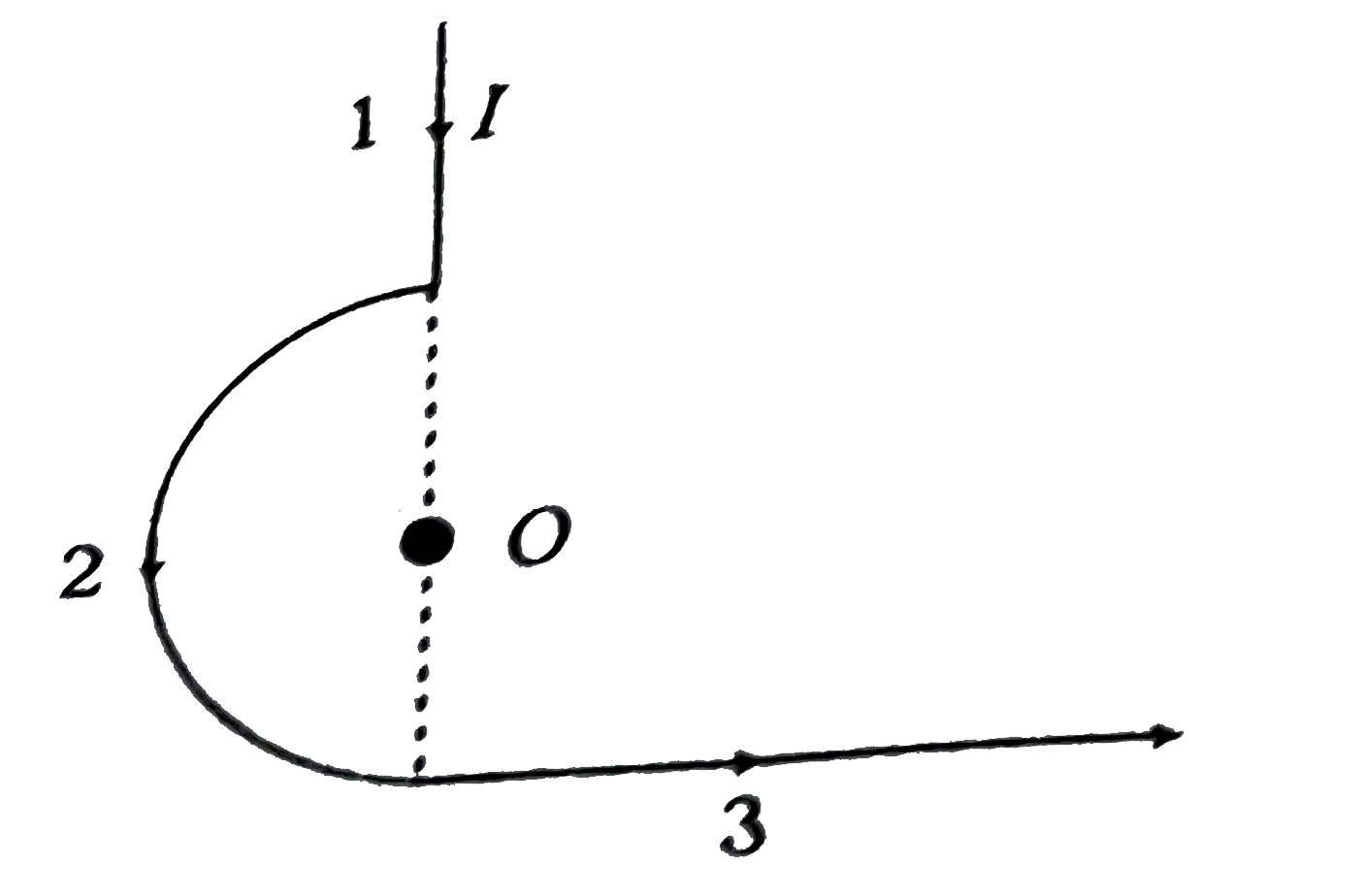
View SolutionTwo identical coils carry equal currents have a common centre and their planes are at right angles to each other. The ratio of the magnitude of the resulatant magnetic field at the centre and the field due to one coil is
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionAn electron moves in a circular orbit with a uniform speed `v`.It produces a magnetic field `B` at the centre of the circle. The radius of the circle is proportional to
View SolutionTwo wires of same length are shaped into a square and a circle. If they carry same current, ratio of the magnetic moment is
View SolutionTwo particles `X` and `Y` with equal charges, after being accelerated throuhg the same potential difference, enter a region of uniform magnetic field and describe circular paths of radii `R_(1)` and `R_(2)` respectively. The ratio of the mass of `X` to that of `Y` is
View SolutionTwo long thin wires ABC and DEF are arranged as shown in Fig. They carry equal currents I as shown. The magnitude of the magnetic field at O is
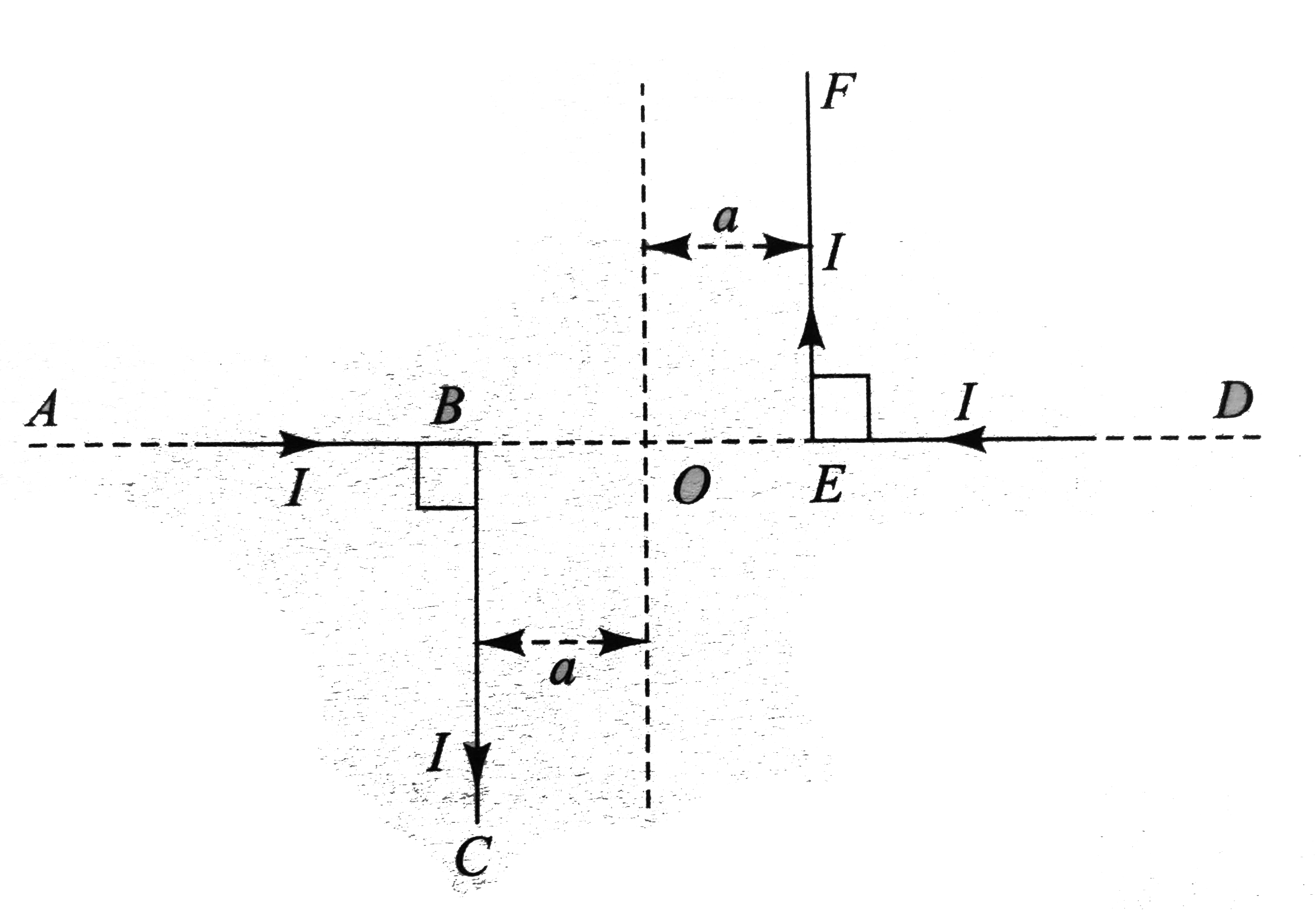
View SolutionA circular conductor of uniform resistance per unit length, is connected to a battery of 4 V. The total resistance of the conductor is `4omega`. The net magnetic field at the centre of the conductor is

View SolutionFigure shows, three long straight wires parallel and equally speed with identical currents. Then, the force acting on each wire due to the other is
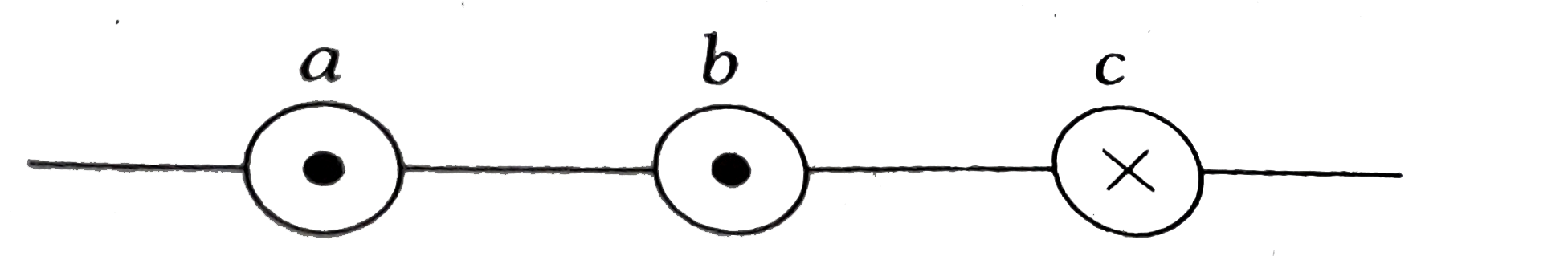
View Solution`A, B` and `C` are parallel conductors of equal length carrying currents `I, I` and `2I` respectively. Distance between `A` and `B` is `x`. Distance between `B` and `C` is also `x`. `F_(1)` is the force exerted by `B` on `A` and `F_(2)` is the force exerted by `B` on `C` choose the correct answer

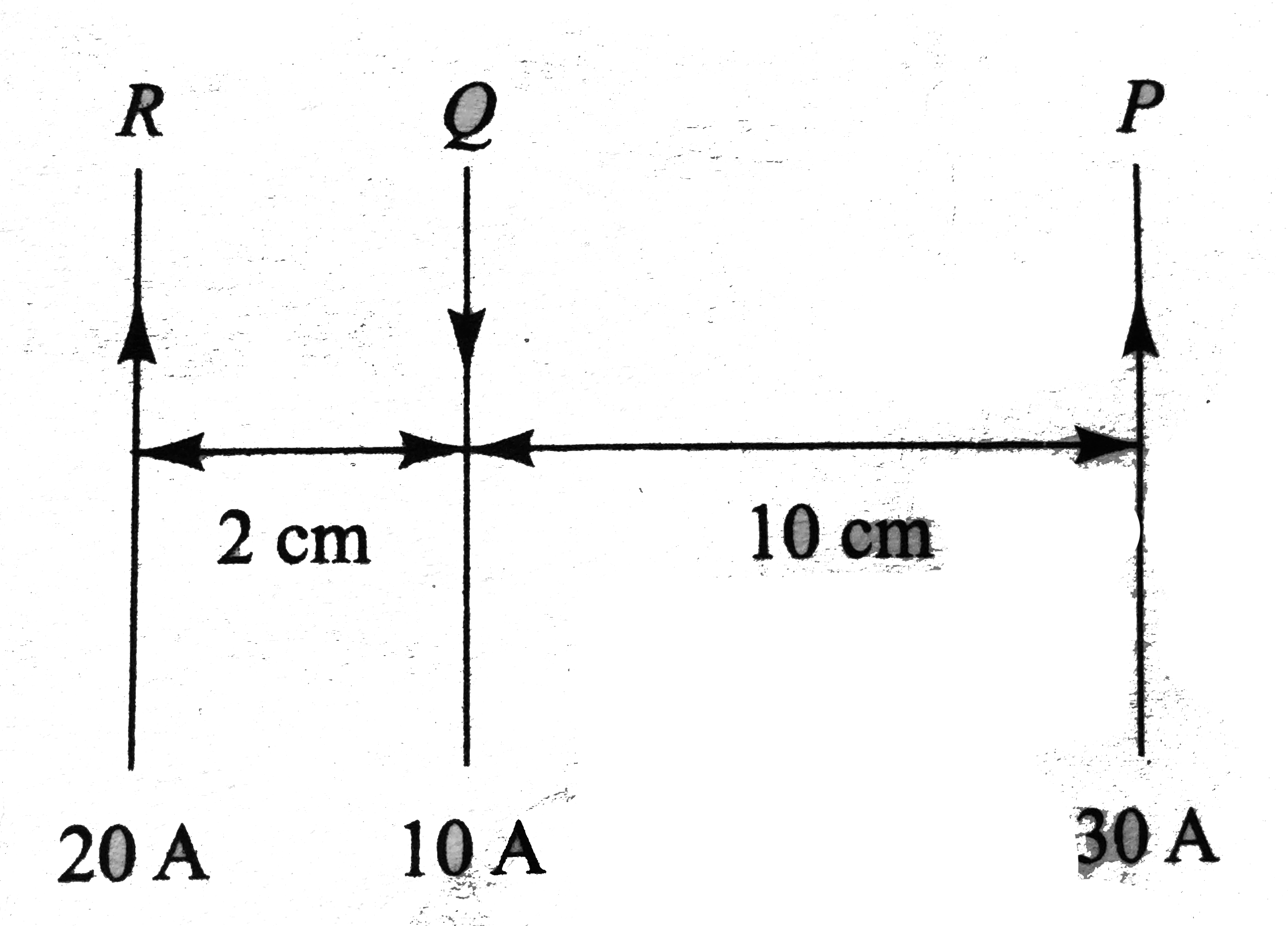
View SolutionThree long, straight and parallel wires are arranged as shown in Fig. The forces experienced by 10 cm length of wire Q is
View SolutionA current of `10` ampere is flowing in a wire of length `1.5m`. A force of `15 N` acts on it when it is placed in a uniform magnetic field of `2` tesla. The angle between the magnetic field and the direction of the current is
View SolutionAn ionized gas contains both positive and negative ions . If it is subjected simultaneously to an electric field along the ` +x` - direction and a magnetic field along the ` +y` - direction and the negative ions towardws `-y` - direction
View SolutionA charged particle P leaves the origin with speed `v=v_0` at some inclination with the x-axis. There is a uniform magnetic field B along the x-axis. P strikes a fixed target T on the x-axis for a minimum value of `B=B_0`. P will also strike T if
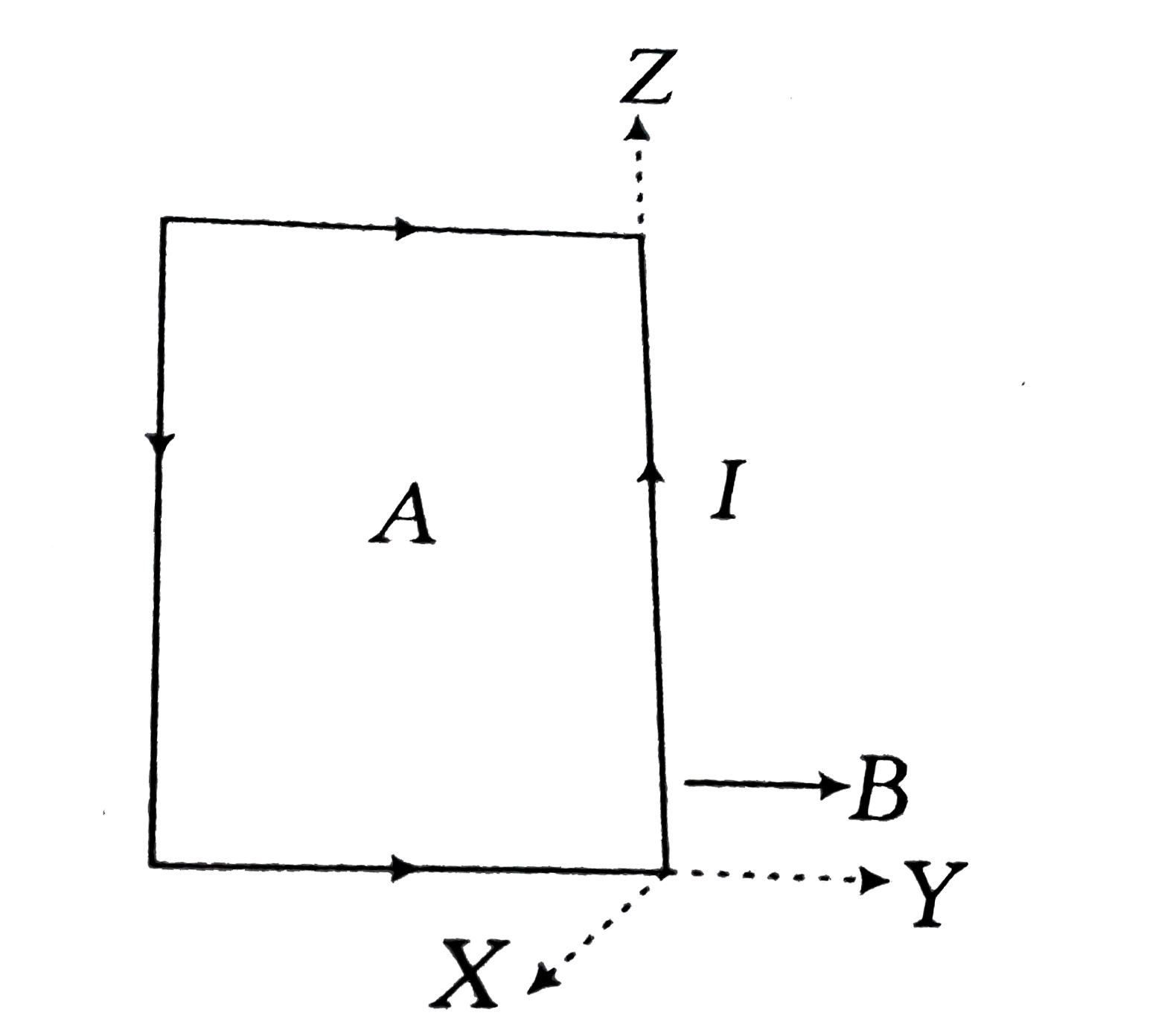
View SolutionThe rectangular coil of area A is in a field B. Find the torque about the Z-axis when the coil lies in the position shown and carries a current I.
View SolutionIn hydrogen atom, the electron is making `6.6xx10^(15) rev//sec` around the nucleus in an orbit of radius `0.528 A`. The magnetic moment `(A-m^(2)) will be
View SolutionTwo infinitely long conductors carrying equal currents are shaped as shown. The short sections are all of equal lengths. The point P is located symmetrically with respect to the two conductors. The magnetic filed at due to any one conductor is B. The total field at P is:

View SolutionA particle of mass m and having a positive charge q is projected from origin with speed `v_(0)` along the positive X-axis in a magnetic field B = `-B_(0)hatK`, where `B_(0)` is a positive constant. If the particle passes through (0,y,0), then y is equal to
View SolutionA 100 turns coil shown in figure carries a current of 2 amp in a magnetic field `B=0.2 Wb//m^(2)`. The torque acting on the coil is
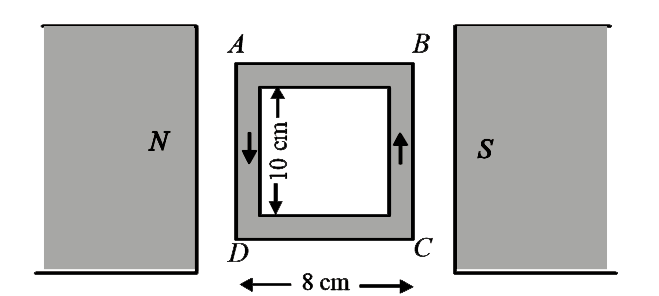
View Solution` H^(+), He^(+) and O^(++)` all having the same kinetic energy pass through a region in which there is a uniform magnetic field perpendicular to their velocity . The masses of ` H^(+), He^(+) and O^(2+)` are `1 amu, 4 amu and 16 amu` respectively . Then
View SolutionA battery is connected between two points `A and B` on the circumference of a uniform conducting ring of radius `r` and resistance `R` . One of the arcs `AB` of the ring subtends an angle `theta` at the centre . The value of the magnetic induction at the centre due to the current in the ring is
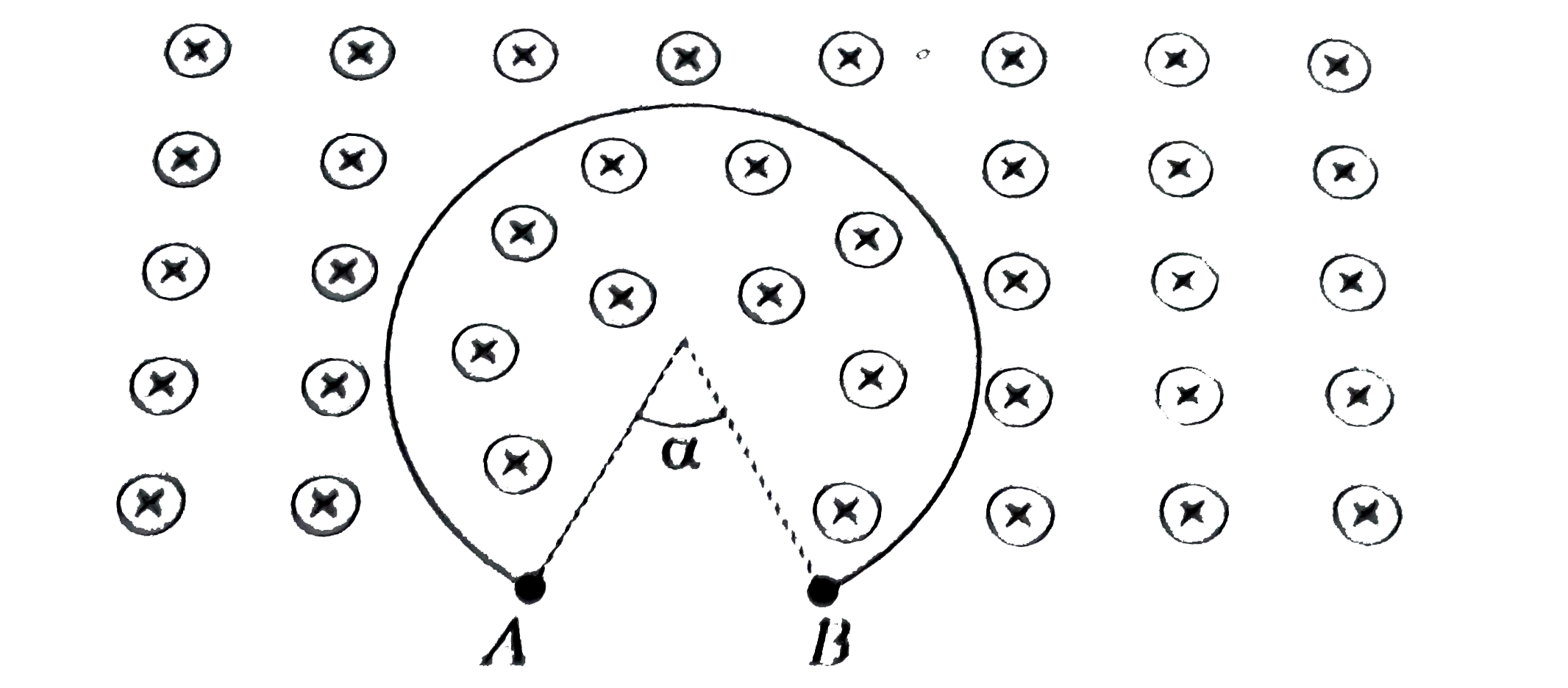
View SolutionA circular loop which is in the form of a major arc of a constant magnetic field B is applied in the vertical direction such that the magnetic lines of forces go into the plane. If R is the radius of circle and it carries a current I in the clockwise direction, then the force on the loop will be
View SolutionTwo protons are projected simultaneously from a fixed point with the same velocity `v` into a region, magnetic there exists a uniform magnetic field. The magnetic field strength is `B` and it is perpendicular to the initial direction of `v`. One proton starts at time t=0 and another proton at `t = (pim)/(2qB)`. The separation between them at time `t = (pim)/(qB)` (where, m and q are the mass and charge of proton), will be approximately
View SolutionA disc of radius R rotates with constant angular velocity `omega` about its own axis. Surface charge density of this disc varies as `sigma = alphar^(2)`, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionA rigid circular loop of radius `r` and mass `m` lies in the `XY-` plane of a flat table and has a current `I` flowing in it. At this particular place. The Earth's magnetic field `vec(B)=B_(x)i+B_(z)k`. The value of `I` so that the loop starts tilting is `:`
View SolutionTwo circular coils 1 and 2 are made from the same wire but the radius of the 1st coil is twice that of the 2nd coil. What is the ratio of potential difference applied across them so that the magnetic field at their centres is the same?
View SolutionA circular loop of mass m and radius r in X-Y plane of a horizontal table as shown in figure. A uniform magnetic field B is applied parallel to X-axis. The current I in the loop, so that its one edge just lifts from the table is
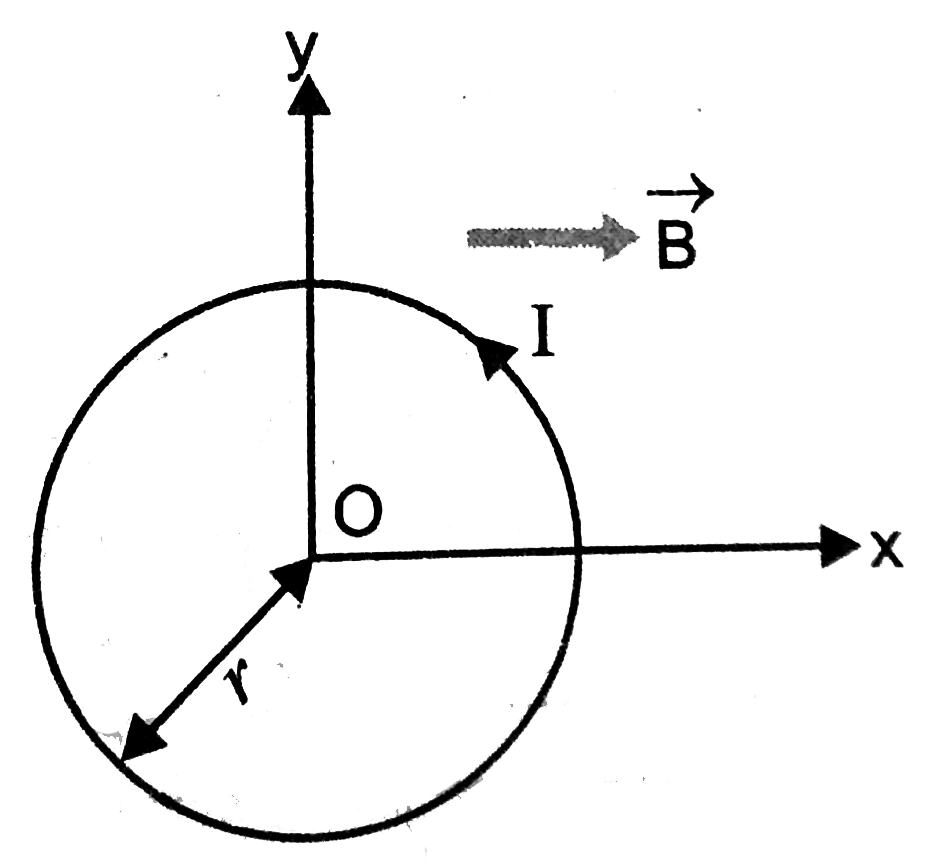
View SolutionA charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
View SolutionThe coil of a moving coil galvanometer has an effective area of 4xx10^(-2)m^(2)`. It is suspended in a magnetic field of `5xx10^(-2)` Wb `m^(-2)`. If deflection in the galvanometer coil is 0.2 rad when a current of 5 mA is passed through it, then
View SolutionA large metal sheet carries an electric current along its surface. Current per unit length is `lambda` . Magnetic field near the metal sheet is.

View SolutionLet current `i=2A` be flowing in each part of a wire frame as shown in Fig. 1.138. The frame is a combination of two equilateral triangles ACD and CDE of side 1 m. It is placed in uniform magnetic field ` B= 4 T` acting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is
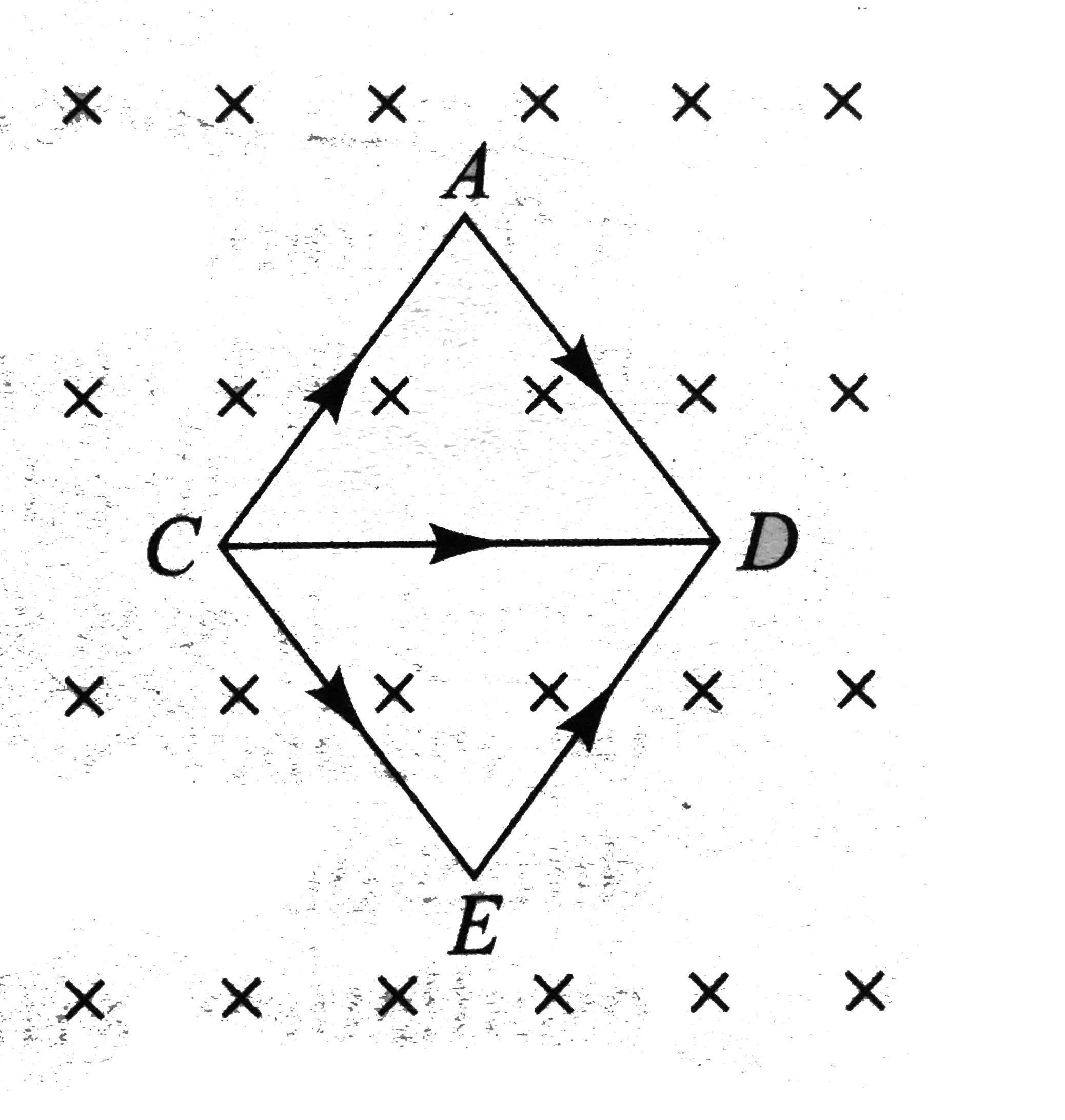
The pithc of the helical path followed by the particle is p. The radius of the helix will be
View SolutionA conducting stick of length 2L and mass m is moving down a smooth inclined plane of inclination `60^(@)` with constant speed 5m/s. A current 2A is flowing in the conductor perpendicular to the paper inwards. A vertically upward magnetic field B exists in space there. The magnitude of magnetic field B is
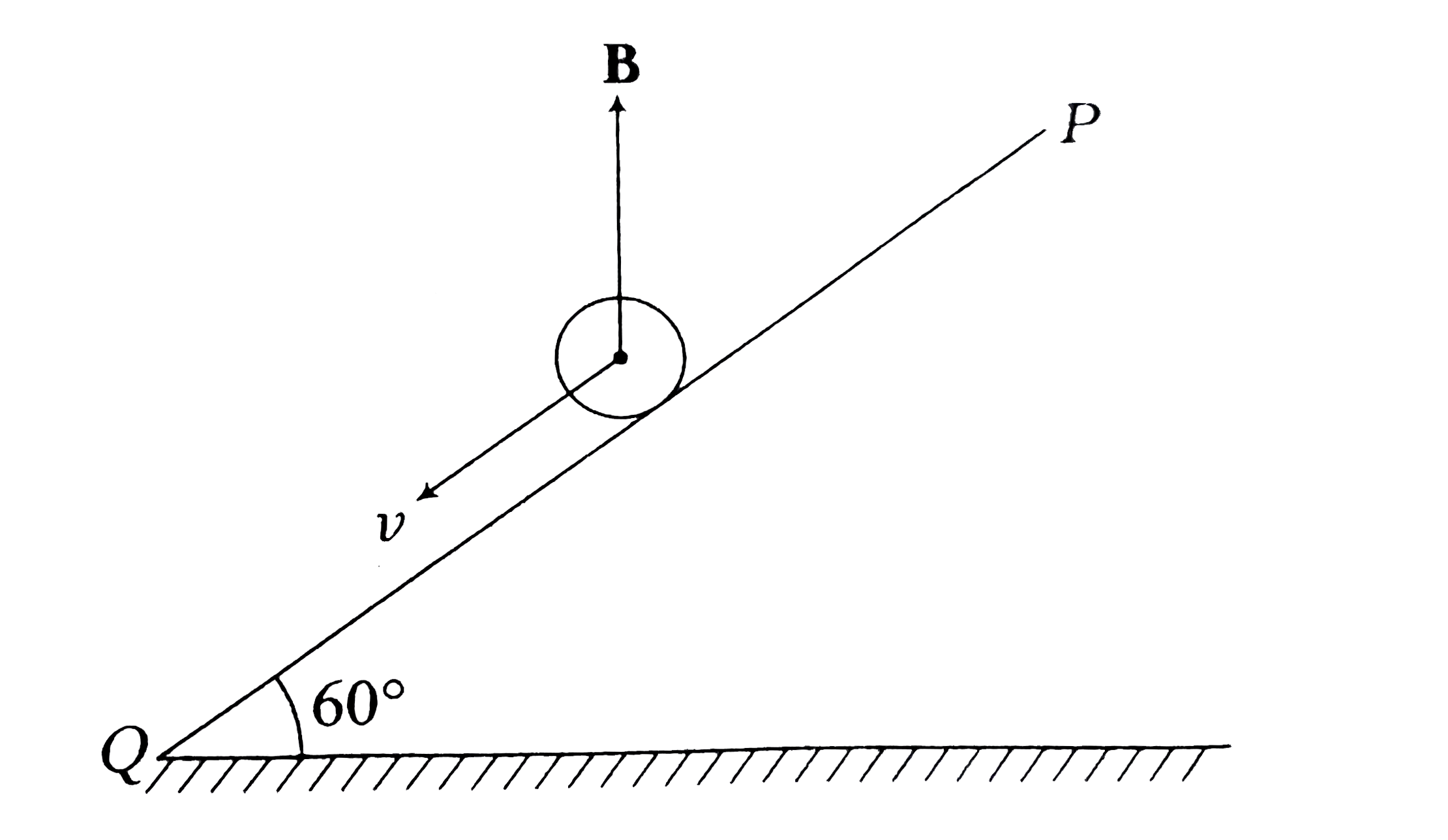
View SolutionA charge q is moving with a velocity `v_(1)=1hati` m/s at a point in a magnetic field and experiences a force `F=q[-hatj+1hatk]` N. If the charge is moving with a velocity `v_(2)=hatj` m/s at the same point then it experiences a force `F_(2)=q(1hati-1hatk)` N. The magnetic induction B at that point is
View SolutionA square frame of side `l` carries a current produces a field `B` at its center. The same current is passed through a circular loop having same perimeter as the square. The field at its center is `B'`, the ratio of `B//B'` is
View SolutionThe magnetic field existing in a region is given by `vecB =B_0(1+(x)/(l))vec k.` A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
View SolutionTwo straight infinitely long current carrying wires are kept along Z-axis at the coordinates (0,a,0) and (0, -a, 0) respectively, as shown in the figure. The current in each of the wire is equal and along negative Z-axis (into the plane of the paper).
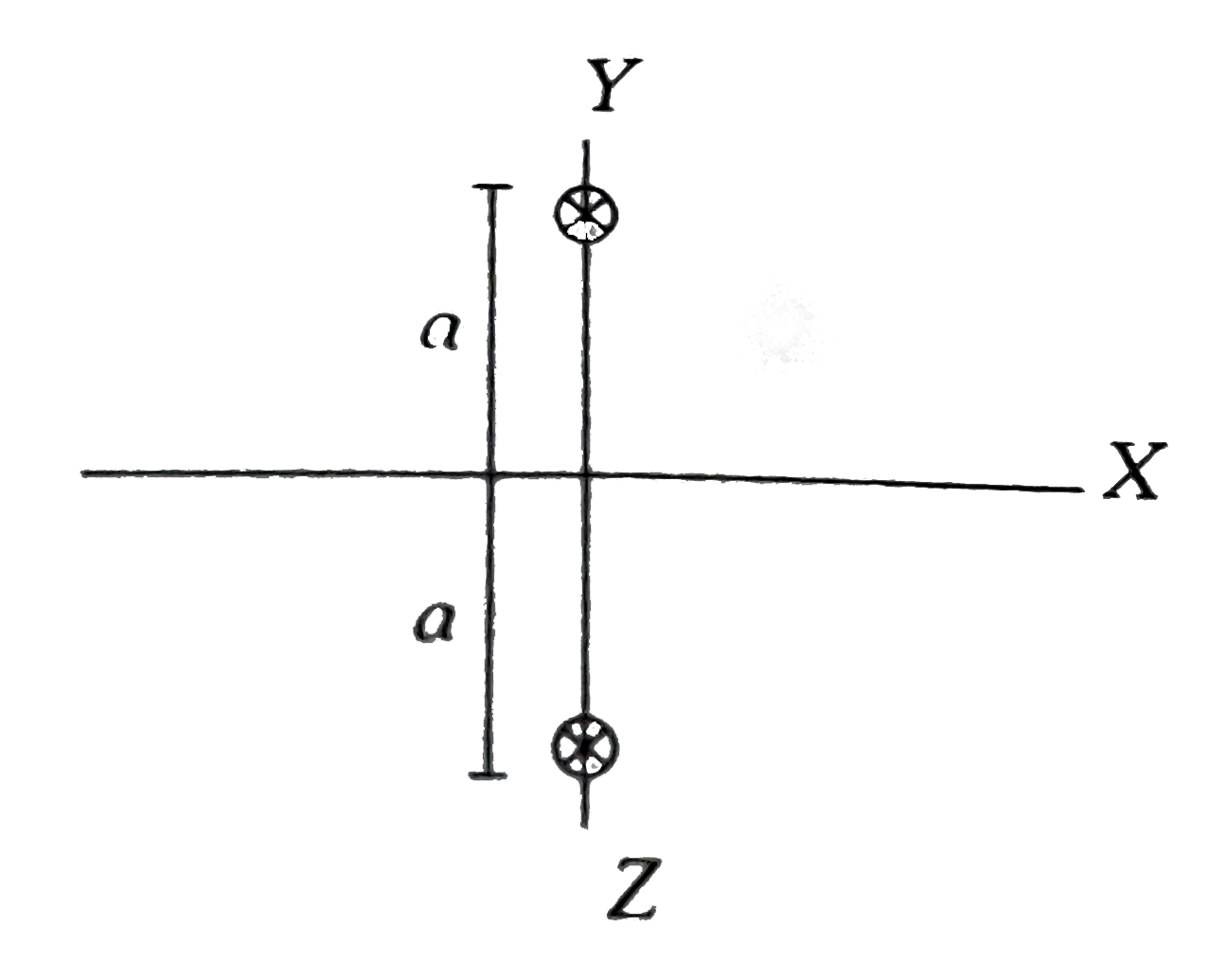
The variation of magnetic field on the X-axis will be approximately
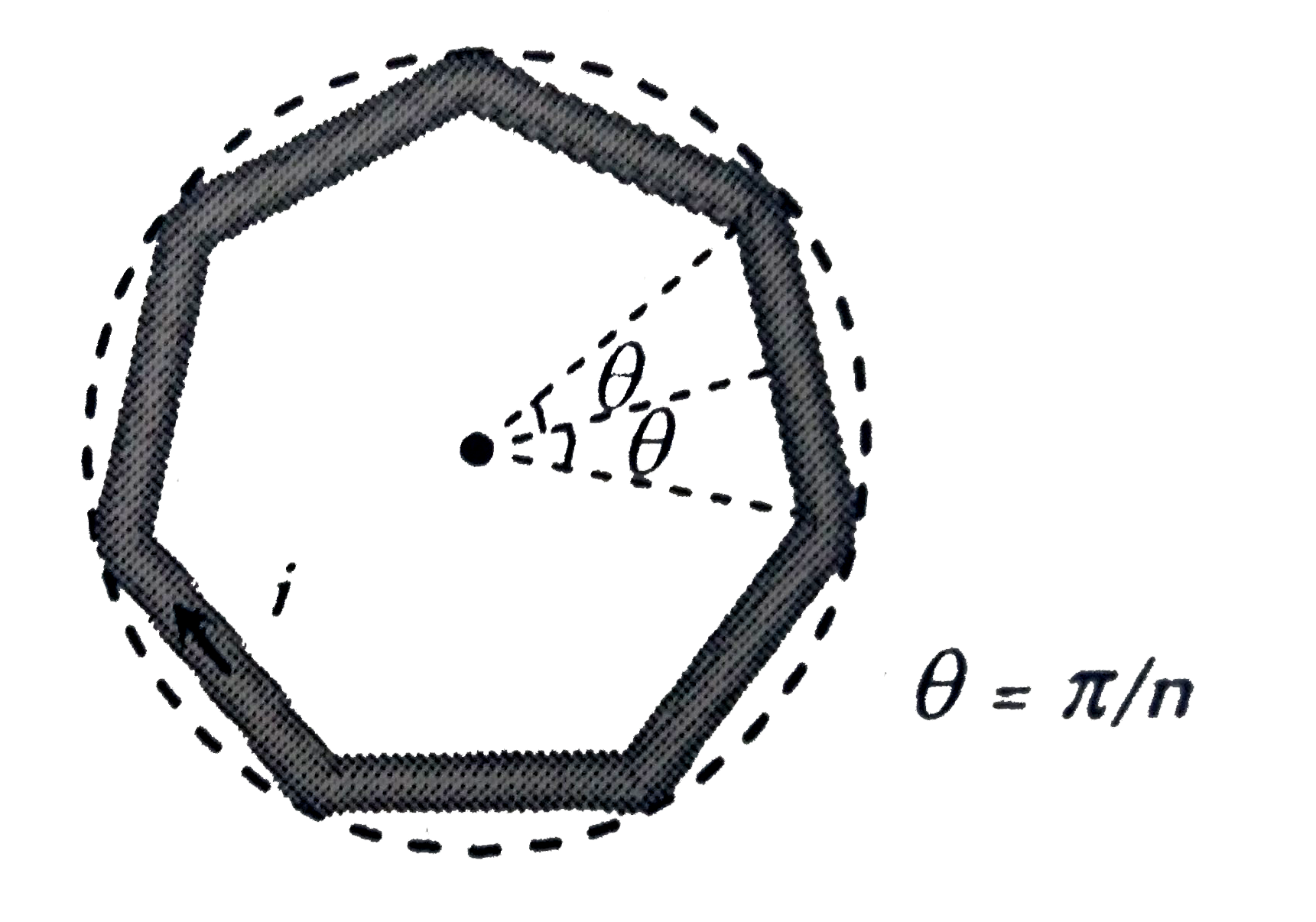
View SolutionIn the following figure a wire bent in the form of a regular polygon of `n` sides is inscribed in a circle of radius `a`. Net magnetic field at centre will be
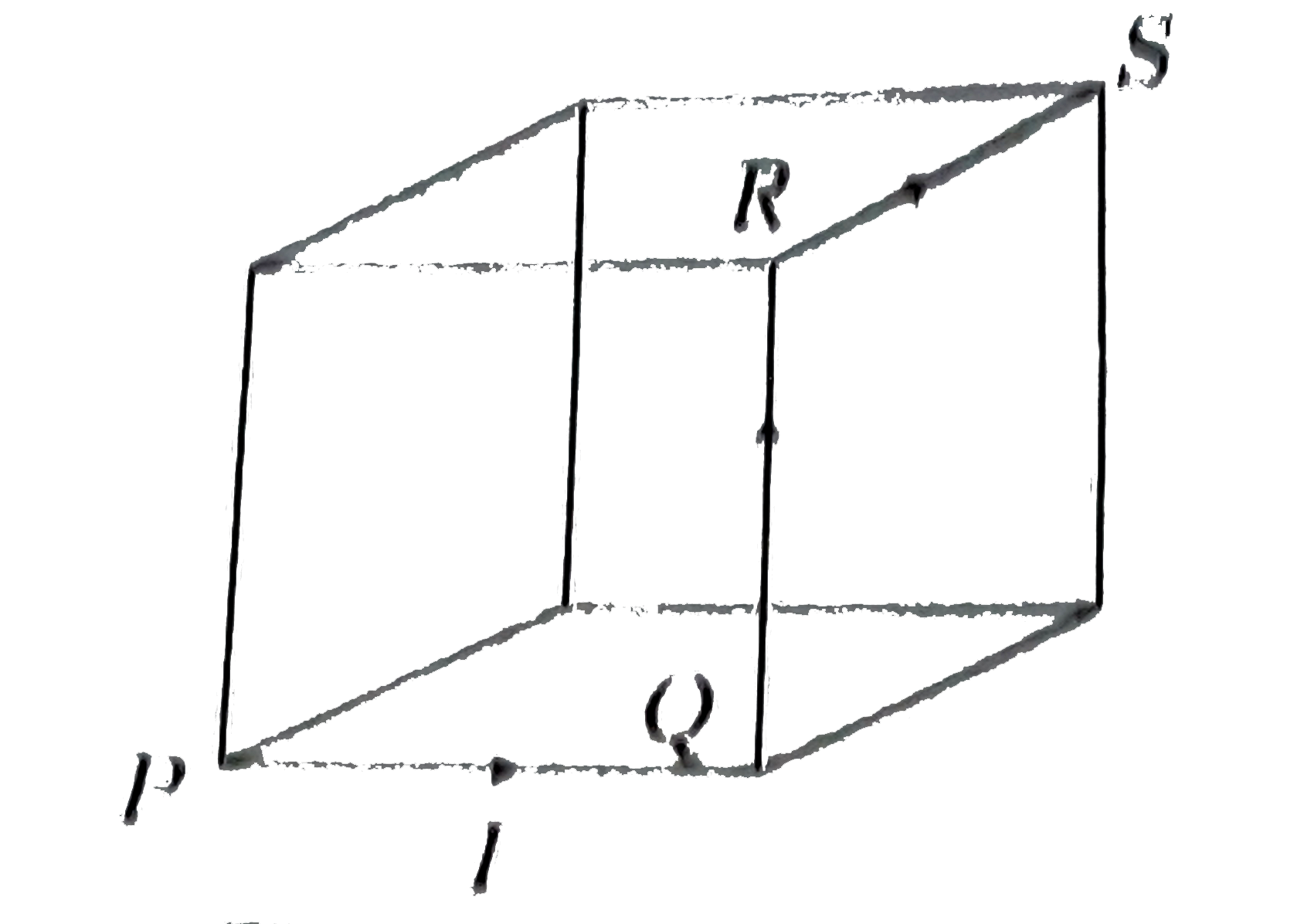
View SolutionA wires PQRS carrying a current I runs along three edges of a cube of side l as shown in figure. There exists a uniform magnetic field of magnitude B along one of the sides of cube. The magnitude of the force acting on the wire is
View SolutionThe magnetic field at the centre of square of side a is
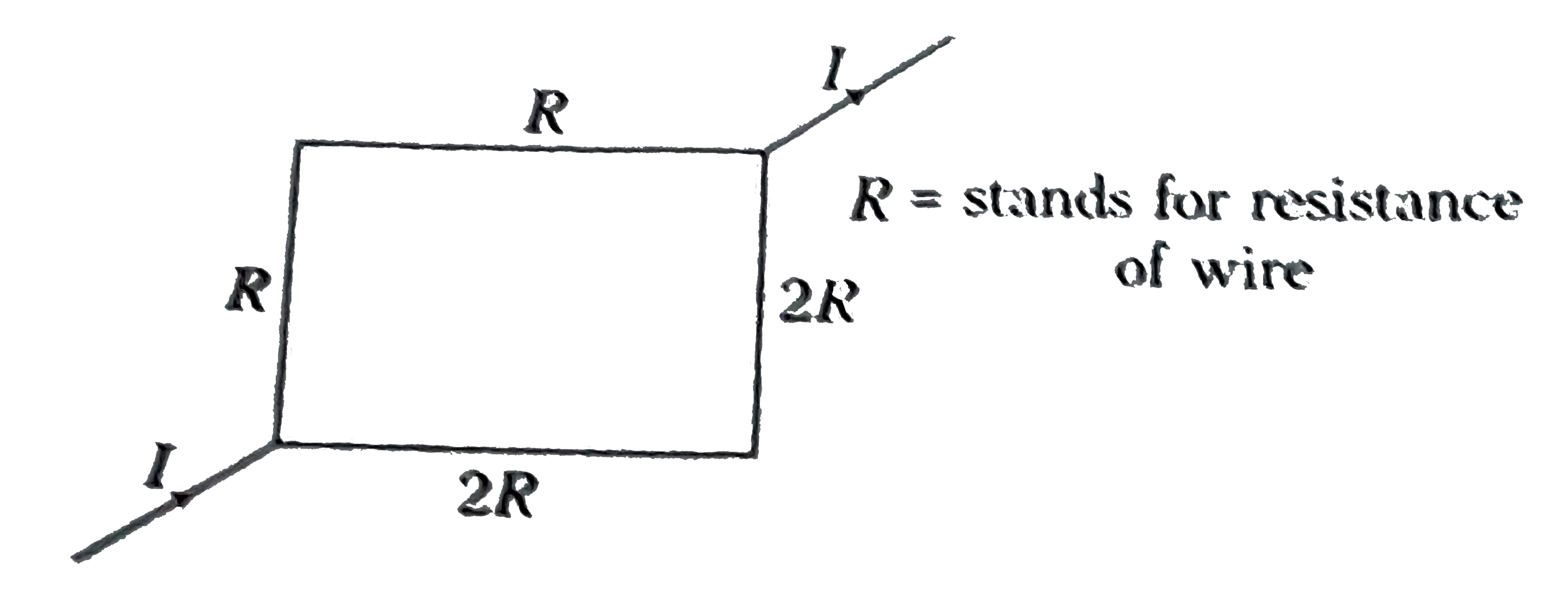
View SolutionA straight rod of mass m and lenth `L` is suspended from the identical spring as shown in the figure The spring stretched by a distance of `x_(0)` due to the weight of the wire The circuit has total resistance `Romega` When the magnetic field perpendicular to the plane of the paper is switched on, springs are observed to extend further by the same distance The magnetic field strength is

View SolutionA particle of specific charge `q//m = (pi) C//kg` is projected from the origin towards positive x-axis with a velocity of `10 m//s` in a uniform magnetic field `vec(B) = -2 hat K` Tesla. The velocity `vec V` of the particle after time `t =1//6` s will be
View SolutionA charged particle enters into a uniform magnetic field with velocity `v_(0)` perpendicular to it , the length of magnetic field is `x=sqrt(3)/(2)R`, where `R` is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
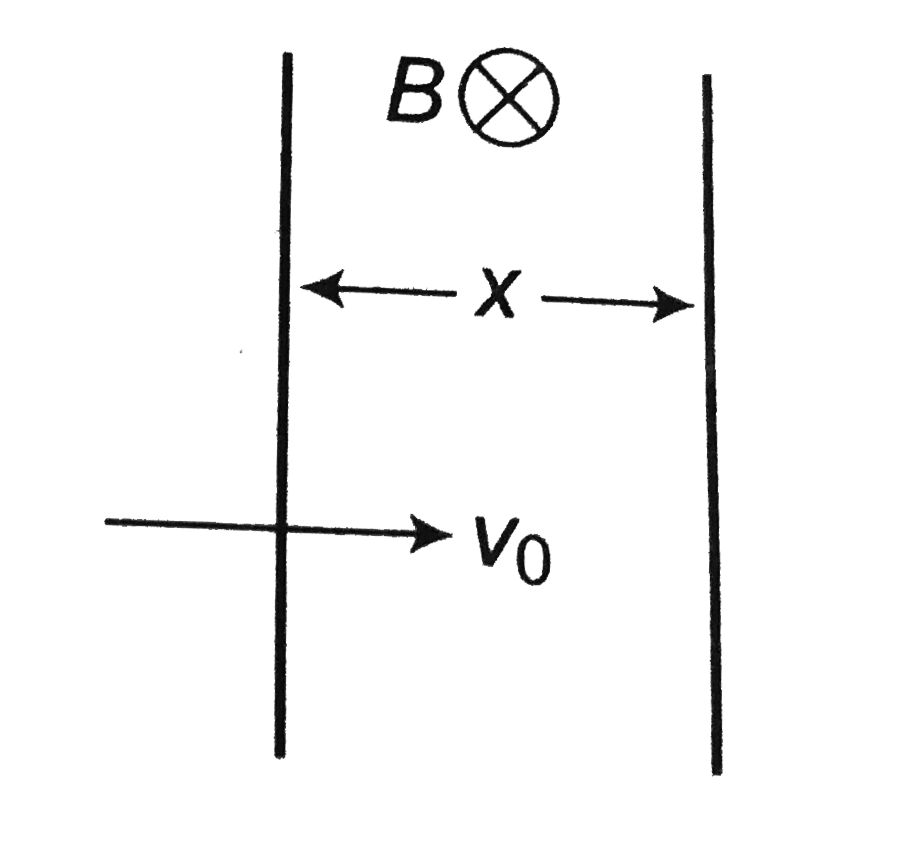
View SolutionA proton moving with a constant velocity passes through a region of space without any changing its velocity. If `E` and `B` represent the electric and magnetic fields and are non zero, respectively. Then, this region of space may have
View SolutionFigure shows three cases: in all case the circular part has radius r and straight ones are infinitely long. For the same current the ratio of field B at centre P in the three case `B_1:B_2:B_3` is
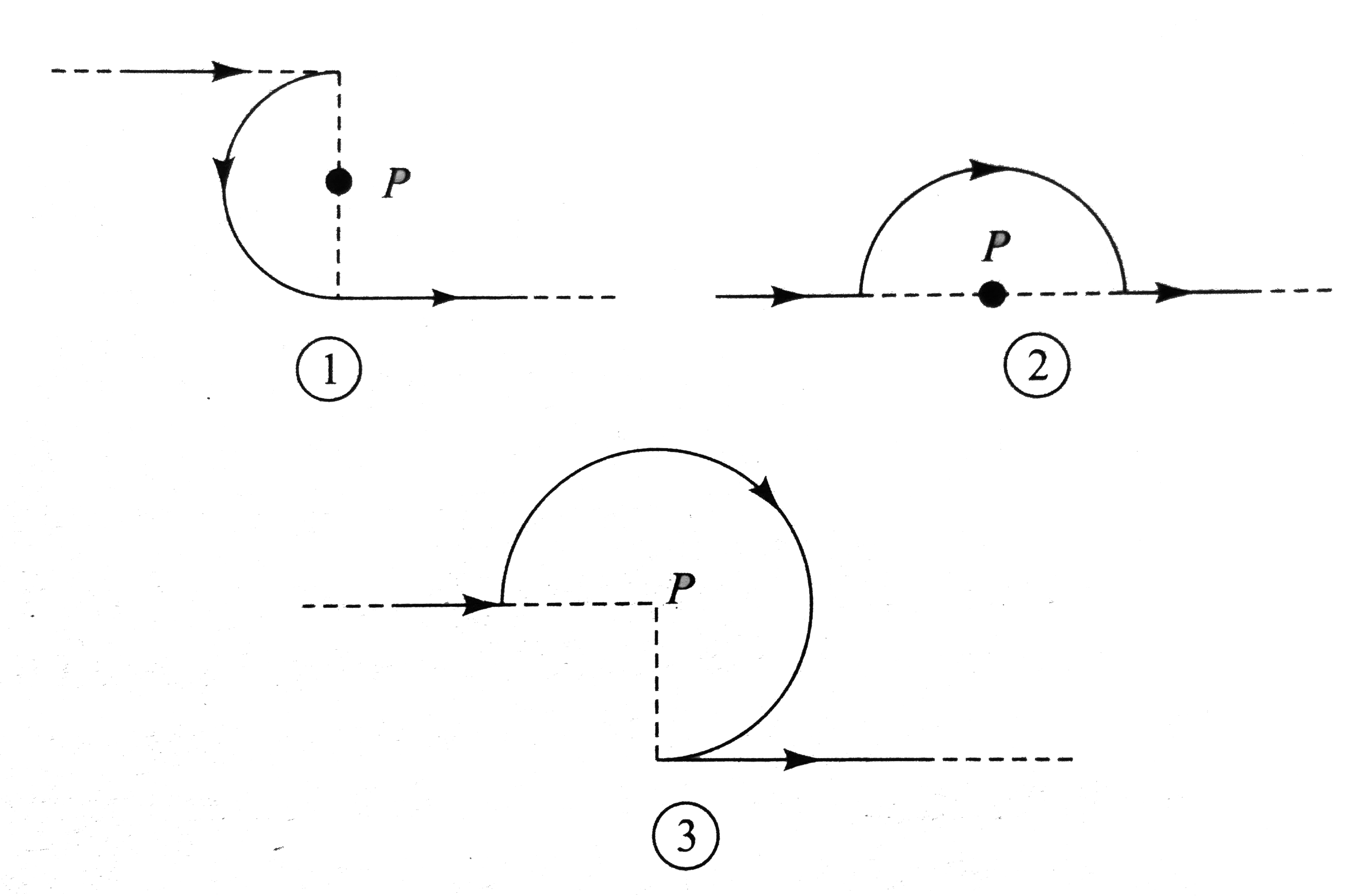
View SolutionA non - popular loop of conducting wire carrying a current `I` is placed as shown in the figure . Each of the straighrt sections of the loop is of the length ` 2a`. The magnetic field due to this loop at the point `P(a, 0 ,a)` points in the direction
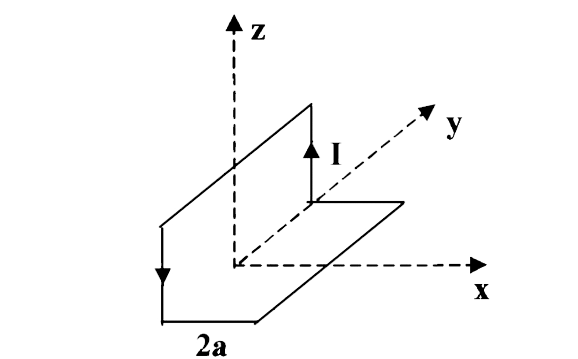
View SolutionA rectangular loop consists of N closed wrapped turns and has dimendions `a xx b`. The loop is hinged along the Y-axis. What is the magnitude of the torque exerted on the loop by a uniform magnetic field `B = B_(0)` directed along the X-axis when current `i = i_(0)` in the direction shown. The torque acting on the loop is
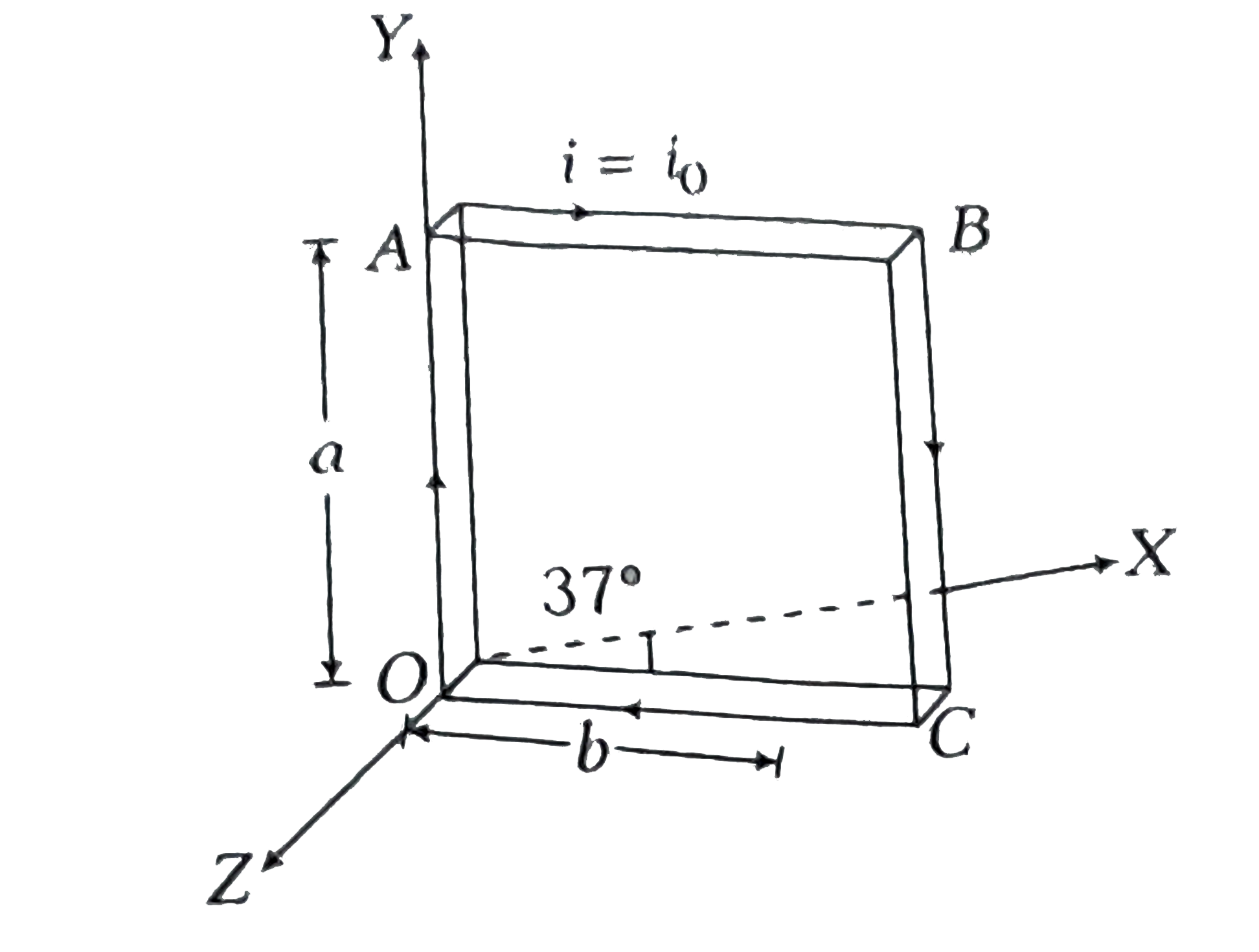
View SolutionA particle of charge -q and mass m enters a uniform magnetic field `vecB` (perpendicular to paper inward) at P with a velocity `v_0` at an angle `alpha` and leaves the field at Q with velocity v at angle `beta` as shown in fig.
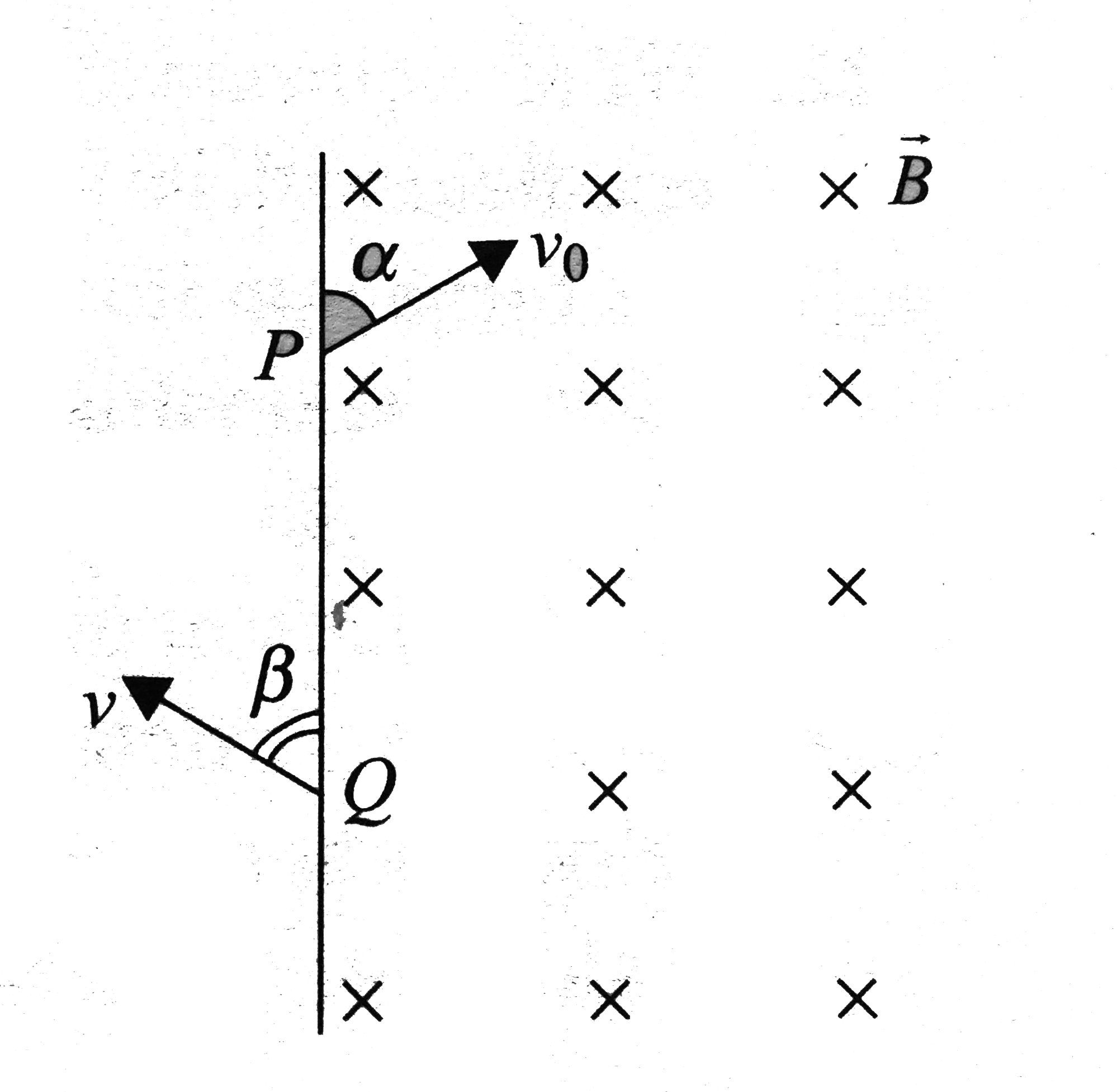
View SolutionA square coil of edge `L` having `n` turns carries a current `i`. it is kept on a smooth horizontal plate. A uniform magnetic field `B` exists in a direction parallel to an edge the total mass of the coil is `M`. What should be the minimum value of `B` for which the coil will start tipping over?
View SolutionA long straight wire along the `z`- axis carries a current ` I` in the negative ` z- direction` . The magnetic vector field ` vec(B)` at a point having coordinates (x,y) in the ` Z = 0` plane is
View Solution
Taking it together questions and complete solutions for chapter MAGNETIC FIELD AND FORCES of DC PANDEY PHYSICS (HINGLISH) of Class 12