Complete Solutions to Example of chapter MAGNETIC FIELD AND FORCES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC FIELD AND FORCES |
| DC PANDEY NEET | Example |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
A current of `10A` is flowing east to west in a long wire kept in the east-west direction. Find magnetic field in a horizontal plane at a distance of (i) `10cm`. North (ii) `20cm` south from the wire, and in a vertical plane at a distance of (iii) `40cm` downwards, (iv) `50cm` upwards.
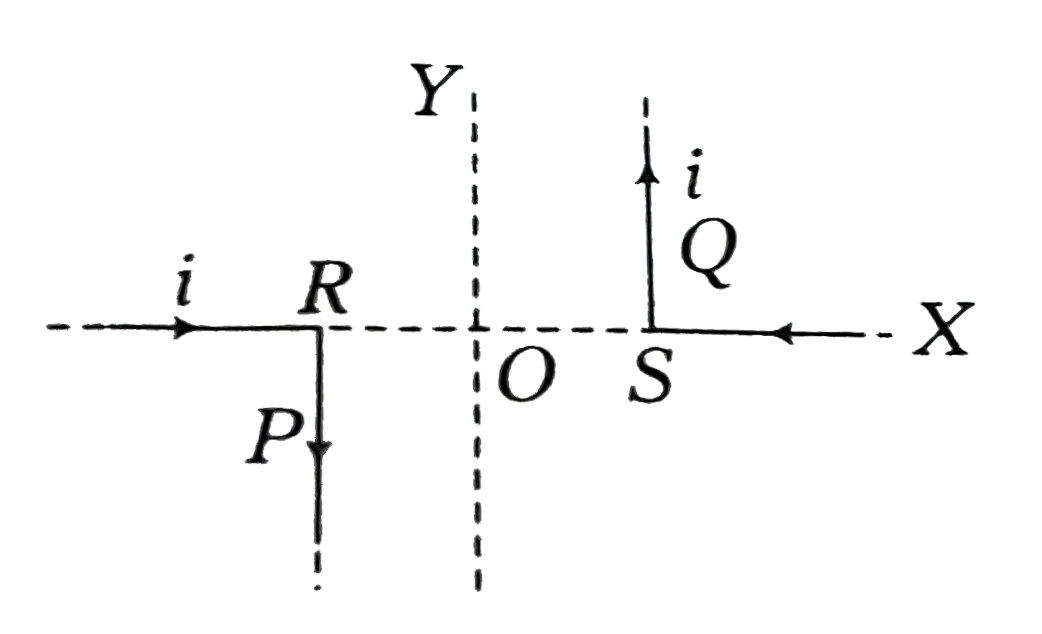
View Solution(i) A pair of stationary and infinitely long bent wires are aplced in the XY- plane as shown.The wires carry currents 10 A each. The segment P and Q are parallel to the Y-axis such as OS =OR = 0.02 m. Find the magnitude field at the origin O
(ii) three long wires carrying 10 A 20 A and 30 A are placed parallel to each other as shown field at P and Q
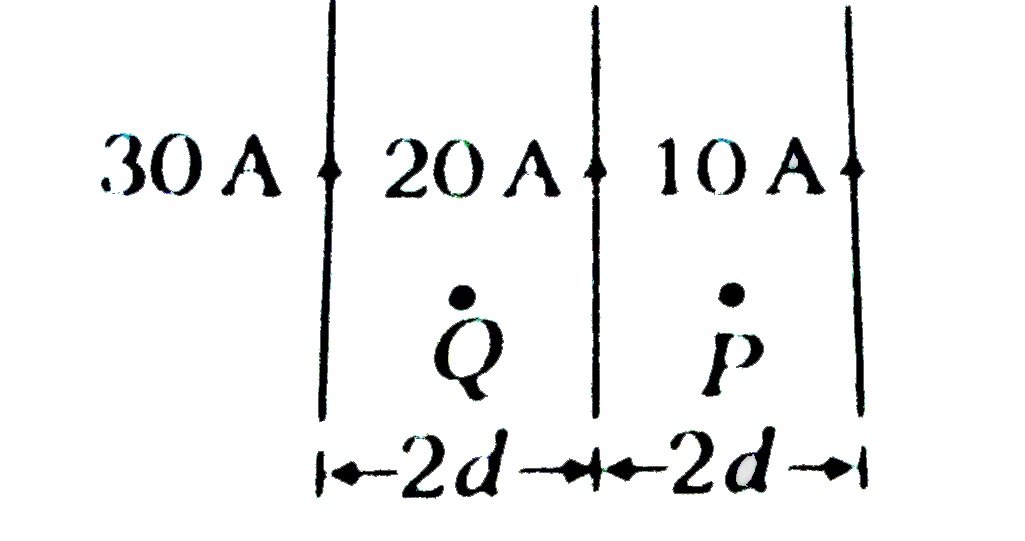
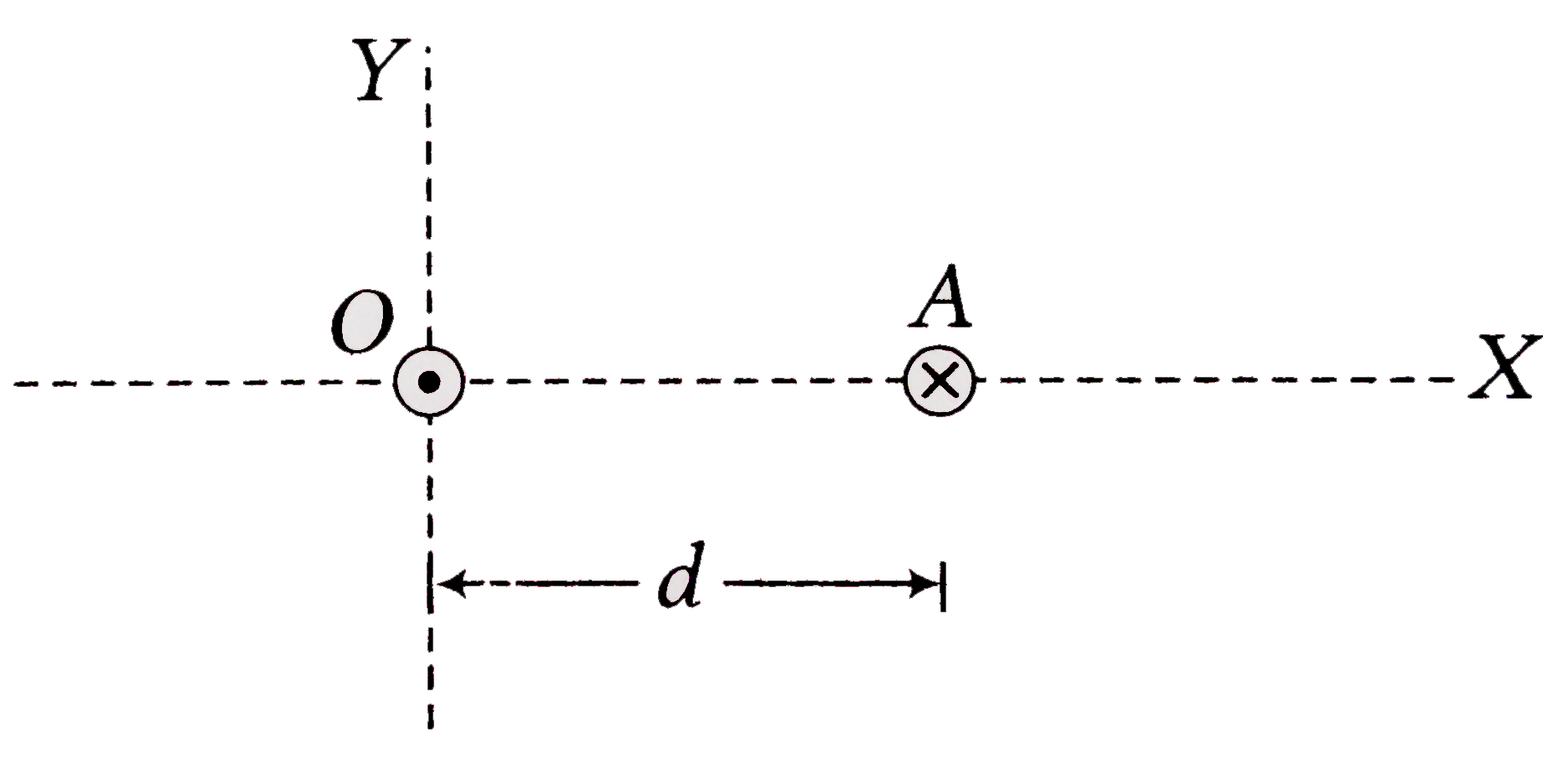
View SolutionTwo long wires carrying same currents in opposite directions are placed at separation D as shown.Predict variation of magnetic field as one moves from the point O and A
View Solution(i) A very long wire carrying a current I is bent at right angles .Find magnetic field at a point lying on a perpendicular to the wire , drawn through the point of bending at a distance d from it
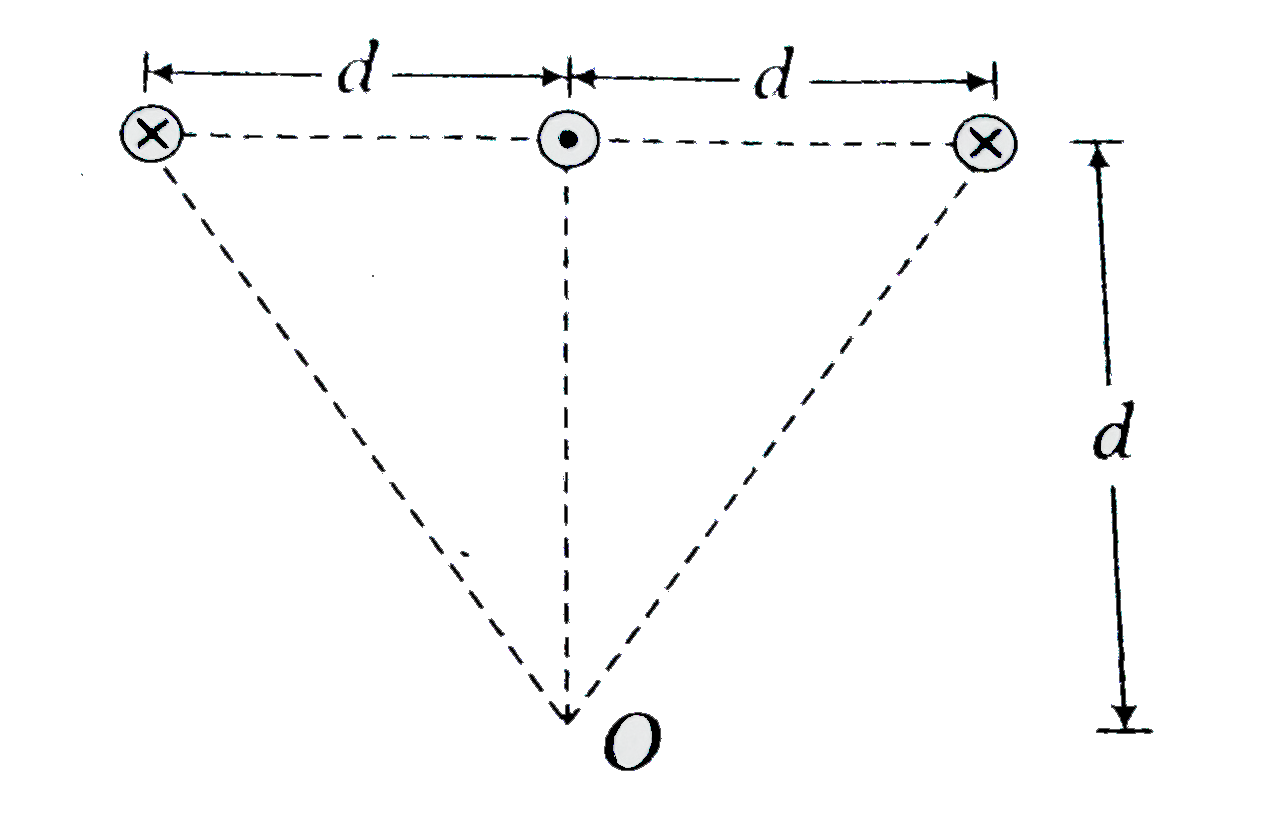
(ii) Three long wires carrying same currect are placed as shown Find magnetic field at O.
View SolutionEvaluate magnitude and direction of magnetic field at a point P in the following cases
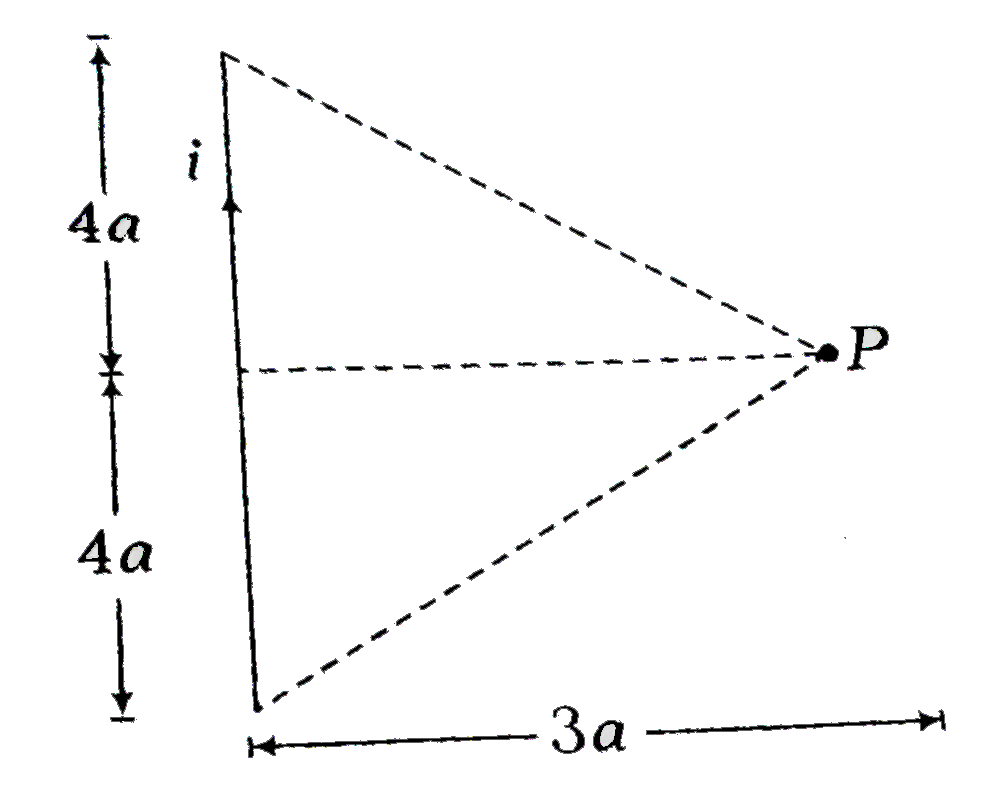
`
View SolutionA wire shaped to a regular hexagon of side `2 cm` carries a current of `2A`. Find the magnetic field at the cetre of the hexagon.
View SolutionA regular polygon of n sides is formed by bending a wire of total length `2 pi r` which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting `n rarr oo` , deduce the expression for the magnetic field at the centre of a circular current.
View SolutionFigure shows a square loop ABCD with edge length `a`. The resistance of the wire ABC is `r` and that of ADC is `2r`. Find the magnetic field B at the centre of the loop assuming uniform wires. `

View SolutionA current path shaped as shown in figure produces a magnetic field at `P`, the centre of the arc. If the arc subtends an angle of `30^@` and the radius of the arc is `0.6 m`, what are the magnitude and direction of the field produced at P if the current is `3.0 A`.
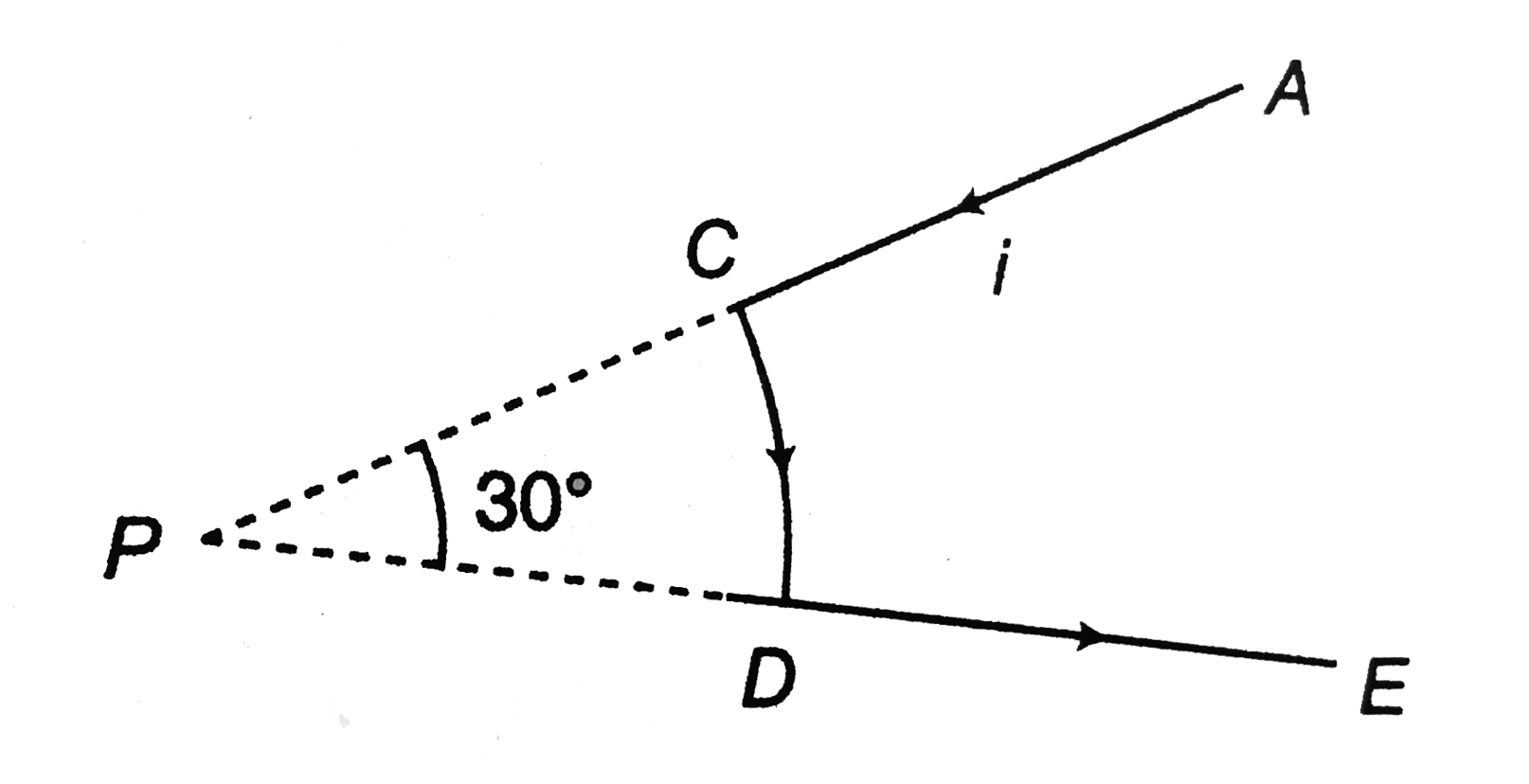
View SolutionFigure shows a current loop having two circular arcs joined by two radial lines. Find the magnetic field B at the centre O.

View SolutionCalculate the magnetic field at point O in each of the following cases:





View SolutionFind the magnitude and direction of magnetic field at point I in the following caese

View SolutionThe magnetic field at the centre of the circular loop as shown in Fig. when a single wire is bent to form a circular loop and also extends to form straight sections is
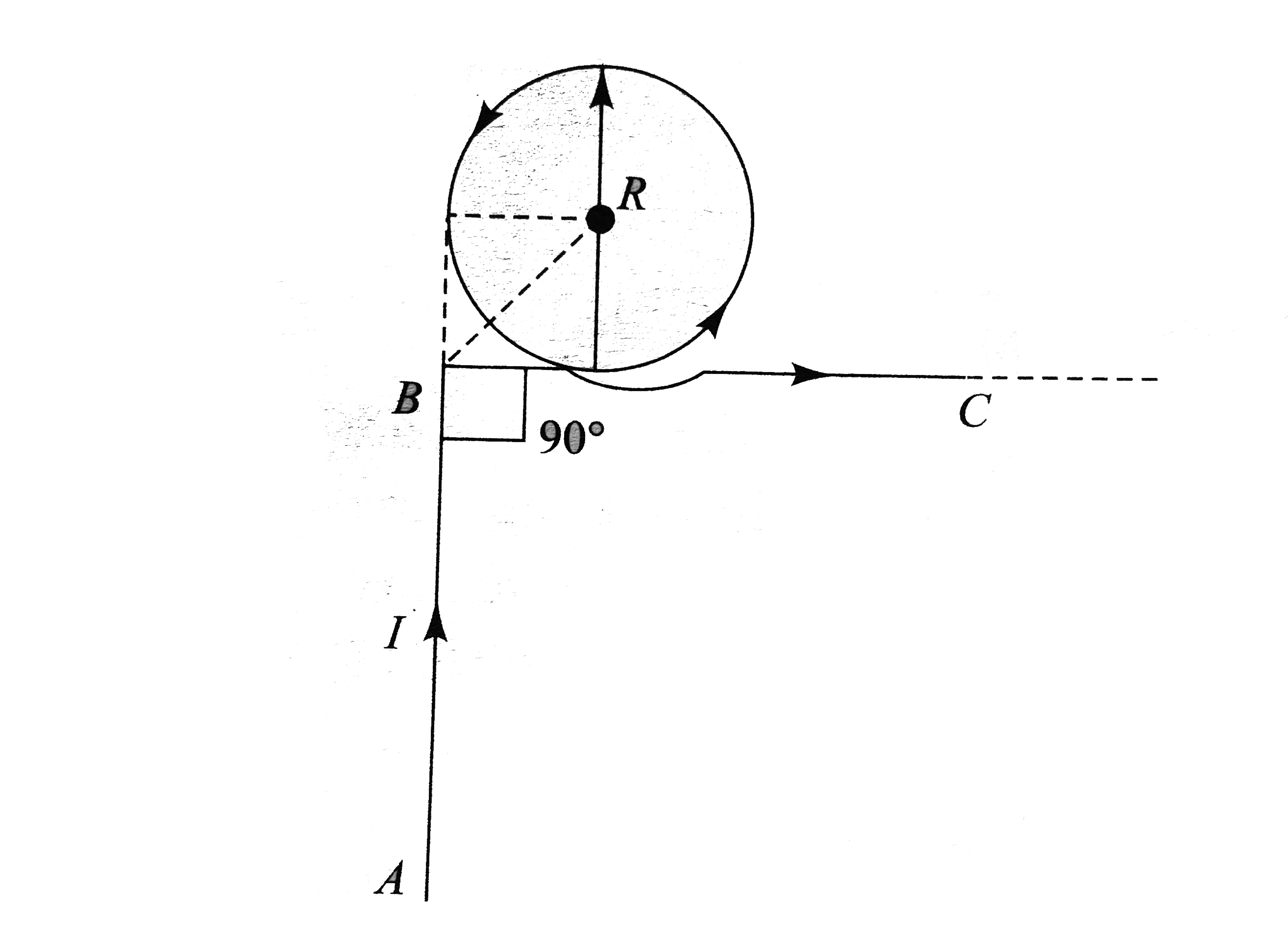
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
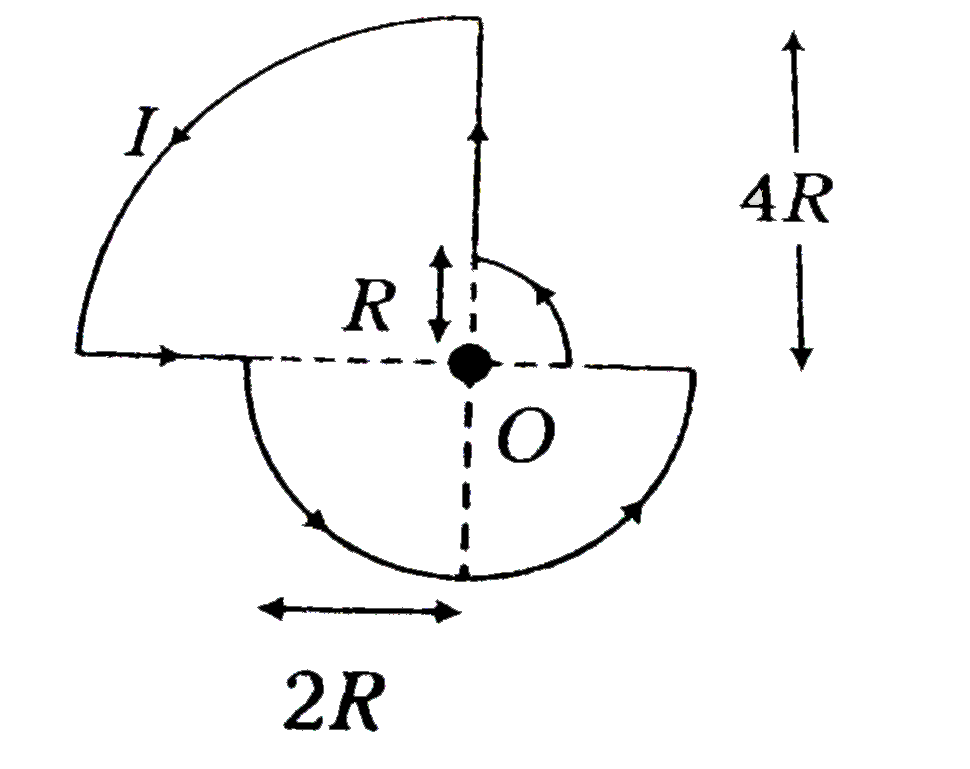
View SolutionThe resistance of wire `ABC` is double of resistance of wire `ADC`. The magnetic field at `O` is

View SolutionThe magnetic field B due to a current- carrying circular loop of radius 12cm at its center is `0.50 xx (10^-4) T`. Find the magnetic field due to this loop at a point on the axis at a distance of 5.0 cm from the centre.
View SolutionTwo concentric coils each of radius equal to `2 pi cm` are placed at right angles to each other ` 3 ampere and 4 ampere` are the currents flowing in each coil respectively. The magnetic induction in `weber//m^(2)` at the centre of the coils will be
`( mu_(0) = 4 pi xx 10^(-7) Wb// A.m)`
View SolutionA 0.8 m long solenoid has 800 turns and a field density of `2.52xx10^(-3)` T at its certre .Find the current in the solenoid
View SolutionA copper wire having resistance 0.01 ohm in each metre is used to wind a 400 turn solenoid of radius 1.0 cm and length 20 cm. Find the emf of a battery which when connected across the solenoid will cause a magnetic field of `(1.0 xx 10^-2)` T near the centre of the solenoid.
View SolutionA coil wrapped around a toroid has inner redius of 20.0 cm amd an outer radius of 25.0 cm .If the wire wrapped makes 800 turns and carries a current of 12.0 A Fimd the maximum and minimum values of the magnetic field within the toroid ?
View SolutionA long straight wire of radius `a` carries a steady current `i`. The current is uniformly distributed across its cross section. The ratio of the magnetis field at `(a)//(2) and (2a)` is
View SolutionA solenoid `50cm` long has 4 layers of windings of `350` turns each. The radius of the lowest layer is `1*4cm`. If the current carried is `6*0A`, estimate the magnitude of magnetic flux density (i) near the centre of the solenoid on its axis, (ii) near the ends on its axis, (iii) outside the solenoid near its centre.
View SolutionA charged particle of specific change (i.e.,Change per unit mass 0 0.2 C/kg has velocity `2hati-3hatjms^(-1)` at some instant in a unifrom magnetic field `5hati+2hatj` (tesla).Find the acceleration of the particle at this instant
View SolutionWhen a proton has a velocity `v=(2hati+3hatj)xx10^6m/s`, it experience a force `F=-(1.28xx10^-13hatk)` When its velocity is along the z-axis, it experience a force along the `x`-axis. What is the magnetic field?
View SolutionA charged particle projected in a magnetic field
`B=(3hati+4hatj)xx10^-2T`
The acceleration of the particle is found to be
`a=(xhati+2hatj)m/s^2`
find the value of `x`
View SolutionA magnetic field of `(4.0xx10^-3hatk)T` exerts a force `(4.0hati+3.0hatj)xx10^-10N` on a particle having a charge `10^-9C` and moving in te `x-y` plane. Find the velocity of the particle.
View SolutionA charged particle carrying charge `q=10 muC` moves with velocity `v_1=10^6 ,s^-1` at angle `45^@` with x-axis in the xy plane and experience a force `F_1=5sqrt2 mN` along the negative z-axis. When the same particle moves with velocity `v_2=10^6 ms^-1` along the z-axis, it experiences a force `F_2` in y-direction.
Find the magnitude of the force `F_2`.
View SolutionTwo long parallel wires carrying current ` 2.5 amperes` and `I ampere` in the same direction ( directed into the plane of the paper) are held at `P and Q` respectively such that they are perpendicular to the plane of paper. The points `P and Q` are located at a distance of ` 5 metres and 2 metres` respectively from a collinear point `R` ( see figure)
(i) An electron moving with a velocity of ` 4xx10^(5) m//s ` along the positive ` x- direction ` experiences a force of magnitude `3.2xx10^(-20) N` at the point `R`. Find the value of `I`.
(ii) Find all the positions at which a third long parallel wire carrying a current of magnitude `2.5 amperes` may be placed so that the magnetic induction at `R` is zero.
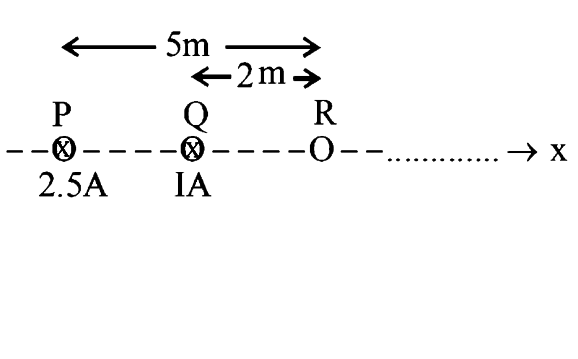
View SolutionWhat is the value of `B` that can be set up at the equator to permit a proton of speed `10^7m//s` to circulate around the earth?
`[R=6.4xx10^6m,m_p=1.67xx10^-27kg]`
View SolutionA proton and ` alpha` - particle are accelerated with same potential difference and they enter in the region of constant magnetic field `B` perpendicular to the velocity of particles. Find the ratio of radius of curvature of ` alpha` - particle`.
View SolutionA charged particle having mass m and charge q is acceleration by a potential difference V, it files through a uniform tranverse magnetic field b.The field occupies a region of space d.Find the time interval for which it remains inside the magnetic field
(i) An `alpha` particle is acceleration by a potential difference of `10^(4)`V. Find the change in tis direction of motiom if it enters normally in a region of thicknees 0.1 , having transverse magnetic induction of `0.1T(m_(aplha)=6.4xx10^(-27)kg)`
(ii) a 10 g bullet having a charge of `4muC` is fired at a speed `270ms^(-1)` in a horizontal direction,A vertical magnetic field as it travels through 100 m .Make appropriate approximations
View SolutionA beam of protons with a velocity of `4 X 10 ^5 ms^(-1)` enters a uniform magnetic field of 0.3 T. The velocity makes an angle of `60^@` with the magnetic field. Find the radius of the helicla path taken by the proton beam and the pitch of the helix.
View SolutionA beam of protons with a velocity `4 xx 10^(5) m//sec` enters a uniform magnetic field of `0.4 T` at an angle of `37^(@)` to the magnetic field. Find the radius of the helical path taken by proton beam. Also find the pitch of helix.
`sin 37^(@) = 3//5 cos 37^(@) = 4//5`. `m_(p) ~= 1.6 xx 10^(-27) kg`.
View SolutionA beam of protons with a velocity of `4 X 10 ^5 ms^(-1)` enters a uniform magnetic field of 0.3 T. The velocity makes an angle of `60^@` with the magnetic field. Find the radius of the helicla path taken by the proton beam and the pitch of the helix.
View SolutionA charged particle `(q,m)` enters uniform magnetic field B at angle `alpha` shown in figure with speed `v_0`. Find
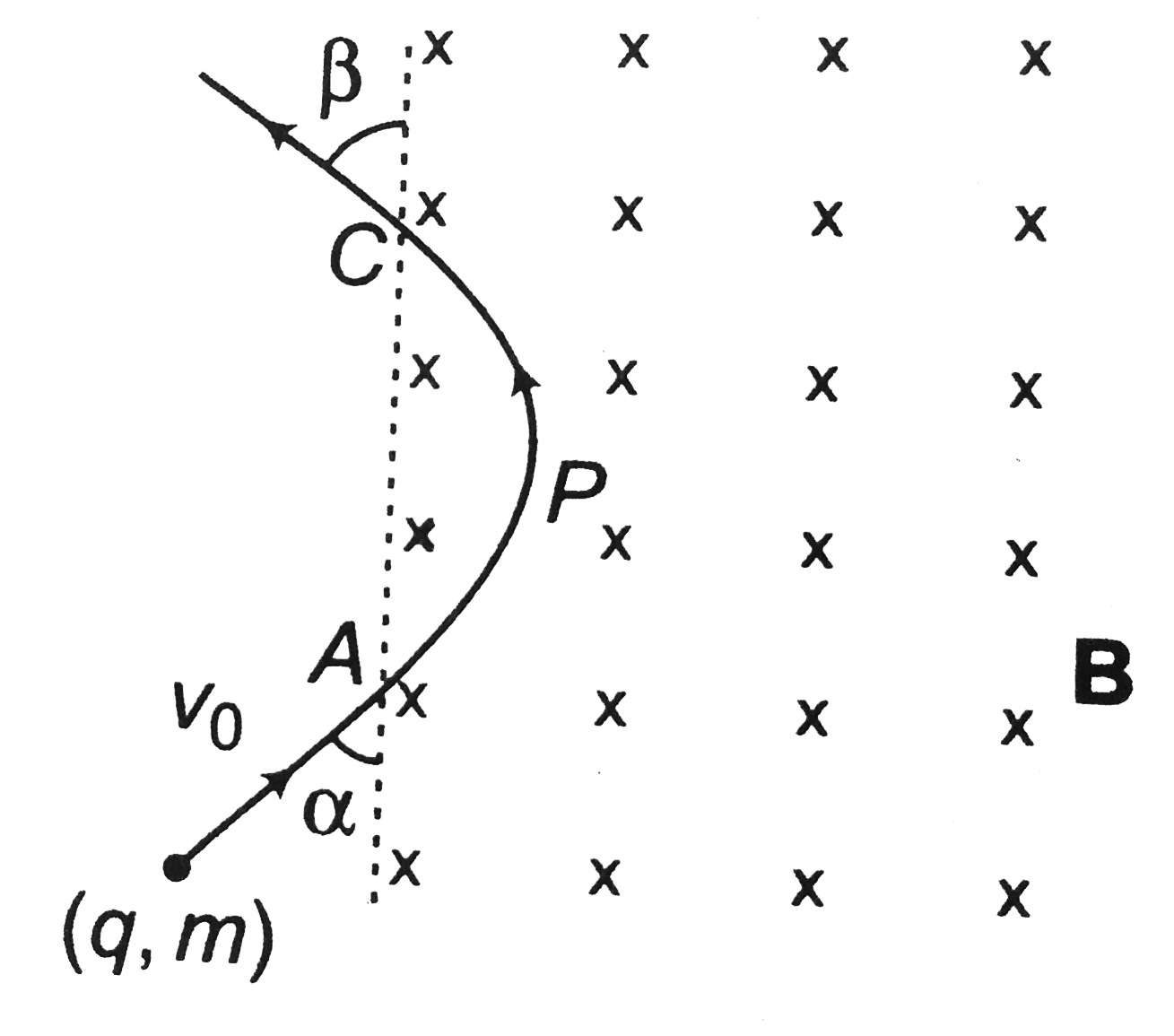
a. The angle `beta` at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance `C`.
View SolutionA charge particle having charge 2 coulomb is thrown with velocity `2hat(i) + 3 hat(j)` inside a region having `vec(E) = 2 hat(j)` and magnetic field `5 hat(k)`. Find the initial Lorentz force acting on the particle
View SolutionA proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic field with `E` and `B` Then the beam strikes a grounded target. Find the force imparted by the beam on the target if the beam current is equal to I .
View SolutionThe magnetic flux density applied in a cyclotron is `3*5T`. What will be the frequency of electric field that must be applied between the dees in order (a) to accelerate protons (b) `alpha`-particles? mass of proton `1*67xx10^(-27)kg`.
View SolutionMagnetic field applied on a cyclotron is `0*7T` and radius of its dees is `1*8m`. What will be the energy of the emergent protons in `MeV`? Mass of proton`=1*67xx10^-27kg`.
View SolutionDeuterons in a cyclotron describes a circle of radius `32.0cm`. Just before emerging from the `D's`. The frequency of the applied alternating voltage is `10MHz`. Find, `(a)` the magnetic flux density `( i.e.,` the magnetic field `), (b)` the energy and speed of the deuterons upon emergence.
View SolutionA wire of length a'a carries a current I along the y-axis.A magnetic field exists given by
`B=B_(0)(3hati+2hatj+hatk)T`
Calculate magnetic force in vector from and its magnitude
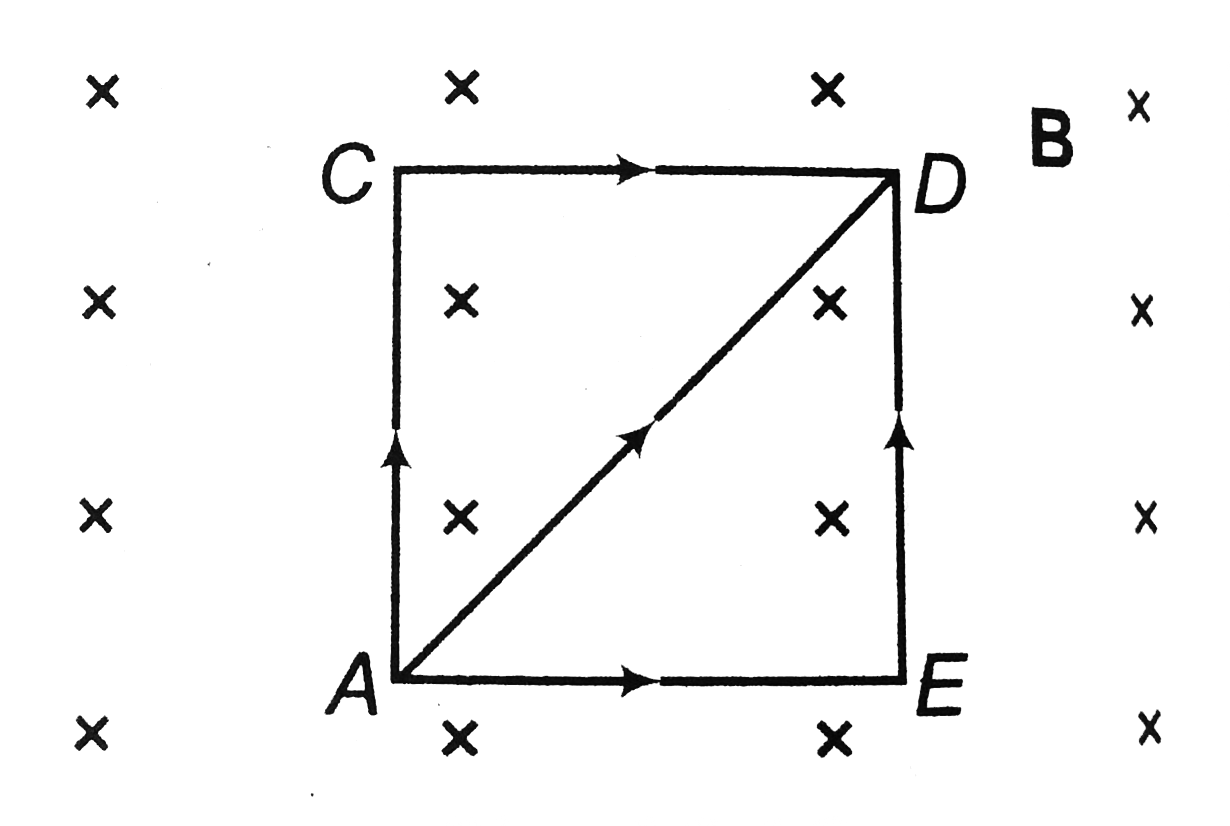
View SolutionA square of side `2.0 m` is placed in a uniform magnetic field `B=2.0 T` in a direction perpendicular to the plane of the square inwards. Equal current `i=3.0 A` is flowing in the directions shown in figure. Find the magnitude of magnetic force on the loop.
View SolutionA straight wire of length 30 cm and mass 60 mg lies in a direction `30^(@)` east of north.The earth's magnetic field at this is horizontal and has a magnitude of 0.8 G.What current must bre passed through the wire,so that it may float in air ?
View SolutionA straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid-air by a uniform horizontal magnetic field B. What is the magnitude of the magnetic field?

View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field `B=1.0T`. The plane of the loop is perpendicular to the magnetic field. Current `i=2A` flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases `a` and `b`. The radius of the loop is 1.0 m

View SolutionA wire, carriying a current I is kept in the x-y plame the curve y -(2 cm) `Asin((2pi)/(lambda)x).A magnetic field B exists in the z - direction.Find the magnitude of the magnetic force on the portion of the wire between z- -0 and `x=lambda//2`
View SolutionA conducting rod of length l and mass m is moving down a smooth inclined plane of inclination `theta` with constant i is flowing in the conductor in a direction perpendicular to paper inwards. A vertically upward magnetic field `vec B` exists in space. Then, magnitude of magnetic field `vec B` is

View SolutionCurrents of `10A, 2A` are passed through two parallel wires `A` and `B` respectively in opposite directions. If the wire `A` is infinitely long and the length of the wire `B` is 2 metre, the force on the conductor `B`, which is situated at `10cm` distance from `A` will be
View SolutionA and B are two infinitely long straight parallel cinductors C is another straight of length 1 m parallel to A and B direction of the force experienced by C

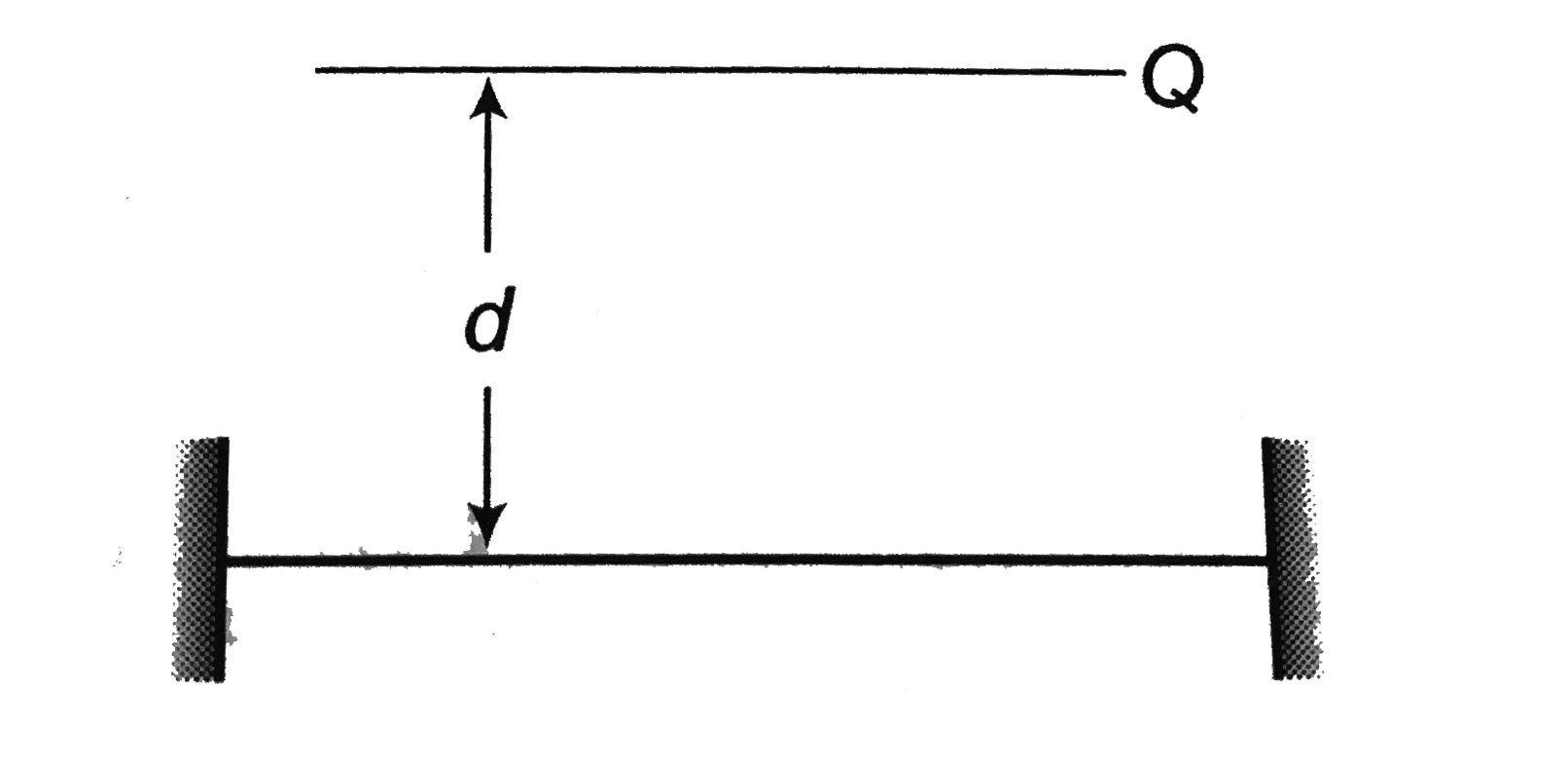
View SolutionA long horizontal wire `P` carries of `50 A`. It is rigidly fixed. Another fine wire `Q` is placed directly above and parallel to `P`. The wieght of wire `Q` is `0.075 N//m` and carries a current of `25 A`. Find the position of wire `Q` from `P` so that the wire `Q` remains suspended due to magnetic repulsion.
View SolutionShows a rod PQ of length 20.0 cm and mass 200g suspended through a fixed point O by two threads of lengths 20.0 cm each. A magnetic field of strenght 0.500 T exists in the vicinity of the wire PQ as shown in the figure. The exists in the vicinity of the wire PQ as shown in the figure. The wires conecting PQ with the battery are loose and exert no force on PQ.(a) find the tension in the threads when the switch S is open. (b) A current of 2.0 A is established when the switch S is closed. Find the tension in the threads now.

View SolutionTwo electrons move parallel to each other with equal speed `'V'` the ratio of magnetic `&` electric force between them is
View SolutionFind the magnetic moment (in `Am^2`) of a thin round loop with current if the radius of the loop is equal to `R = 100 mm` and the magnetic induction at its centre is equal to `B = 6.0 mu T`.
View SolutionFind the magnitude of magetic moment of the current carrying lop `ABCDEFA`. Each side of the loop is `10 cm` long and current in the loop is `i=2.0A`
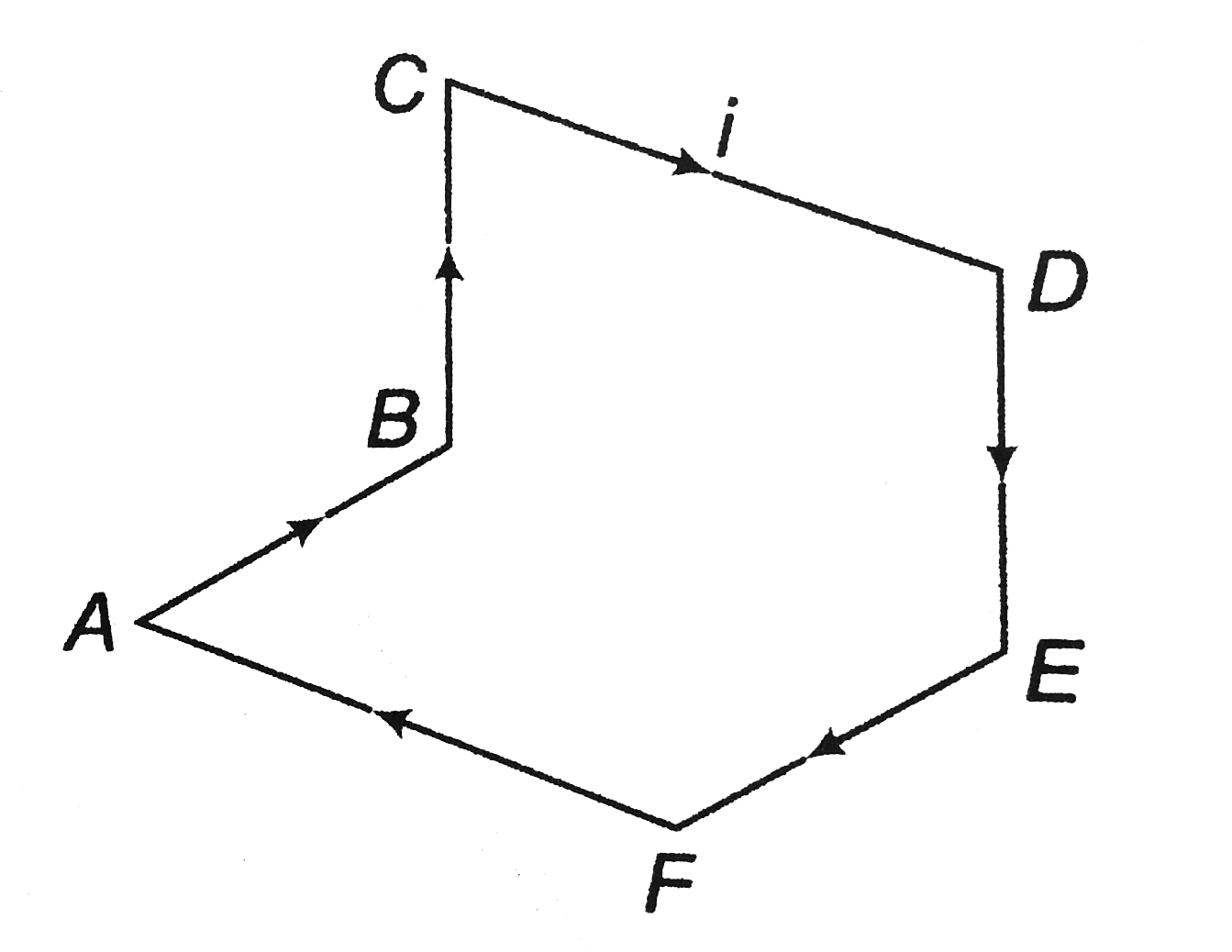
View SolutionIn the Bohr model of the hydrogen atom, the electron circuulates around the nucleus in a path of radius `5xx10^-11m` at a frequency of `6.8xx10^15Hz`.
a. What value of magnetic field is set up at the centre of the orbit?
b. What is the equivalent magnetic dipole moment?
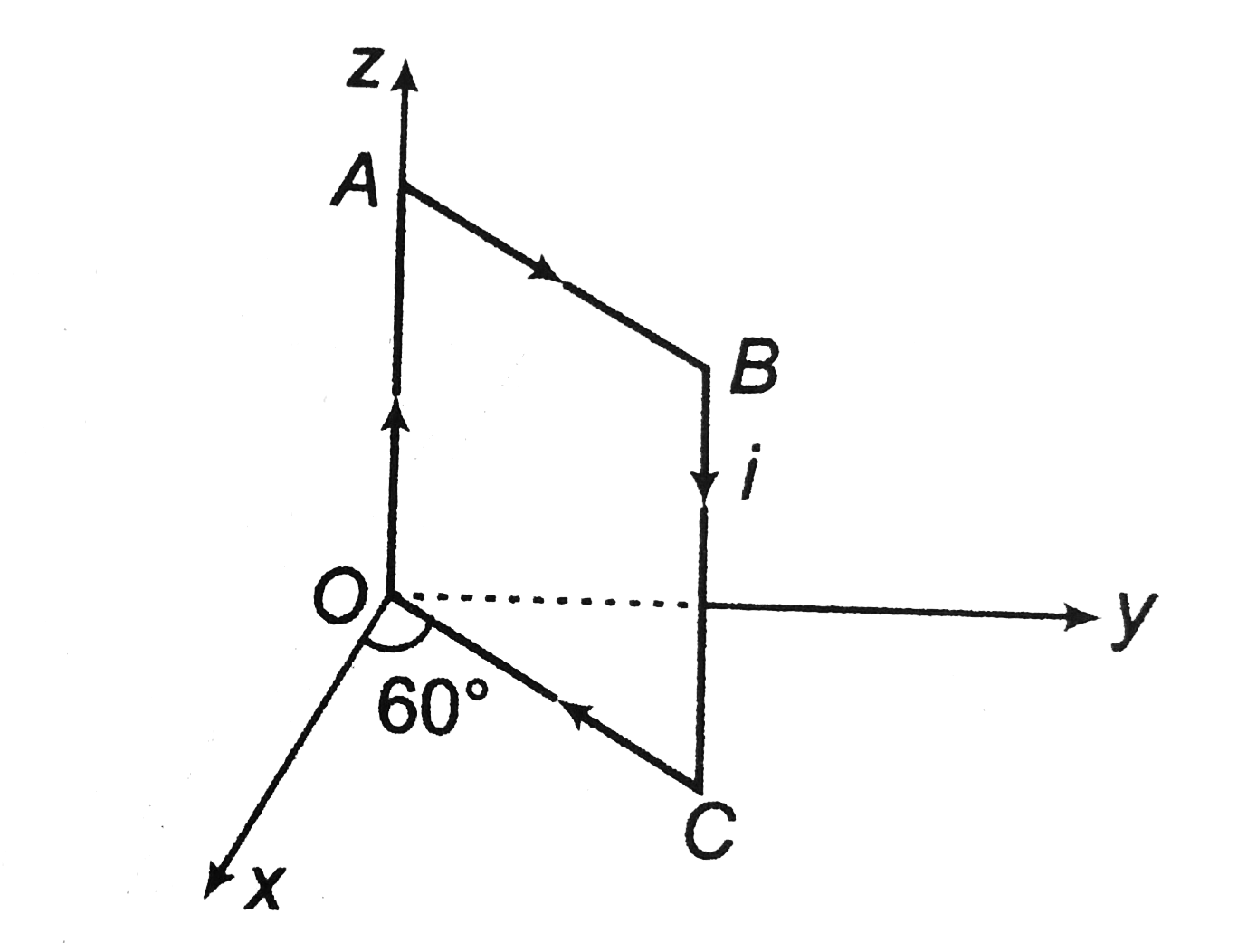
View SolutionA square loop `OABCO` of side of side `l` carries a current `i`. It is placed as shown in figure. Find the magnetic moment of loop.
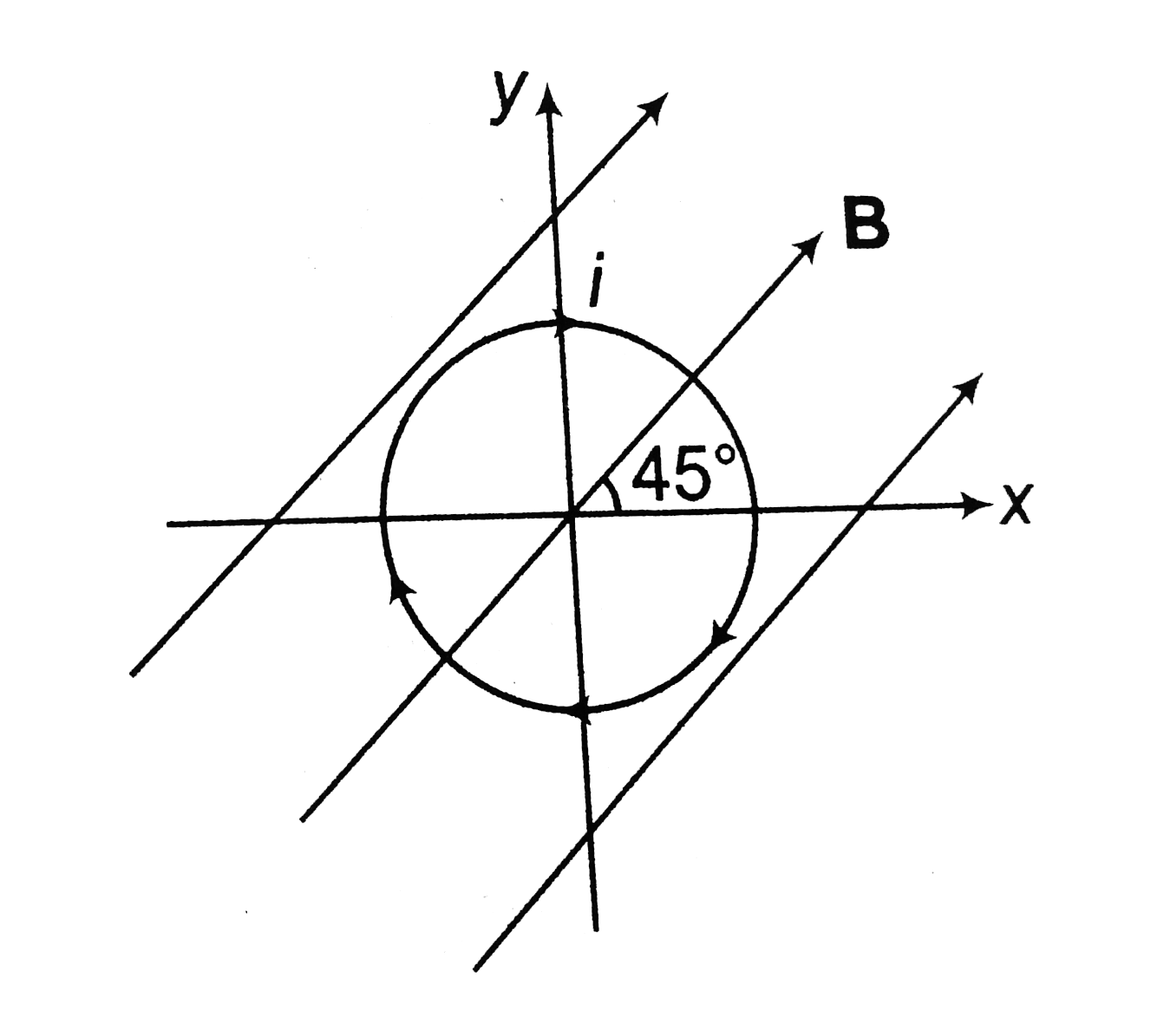
View SolutionA circular loop of radius `R=20` cm is placed in a uniform magnetic field `B=2T` in `xy`-plane as shown in figure. The loop carries a current `i=1.0 A` in the direction shown in figure. Find the magnitude of torque acting on the loop.
View SolutionA uniform magnetic field of `3000G` is established along the positive z-direction. A rectangular loop of sides `10cm` and `5cm` carries a current `12A`. What is the torque on the loop in the different cases shown in the figure. What is the force on each case? Which case corresponds to stable equilibrium?

View SolutionThe coil of a moving coil galvanometer has an effective area of `5xx10^(-2)m^(2)`. It is suspended in a magnetic field of `2xx10^(-2)` `Wbm^(-2)`.If the torsional constant of the senpension fibre is `4xx10^(-9)``"Nmdeg"^(-1)`. Then find its current sensitivity in degree per microampere
View SolutionA moving coil galvanometer has 100 turns and each turn has an area `2.0 cm^2`. The magnetic field produced by the magnet is `0.01 T`. The deflection in the coil is `0.05` radian when a current of `10 mA` is passed through it. Find the torsional constant of the suspension wire.
View SolutionA current of 0.5 A is passed through the coil of a galvanometer having 500 turns and each turns has an average area of `3xx10^(-4) m^(2)` if a torque of 1.5 N-m is required for this coil carrying same current to set it parallel to a magnetic field calculate the strength of the magnetic field
View Solution
Example questions and complete solutions for chapter MAGNETIC FIELD AND FORCES of DC PANDEY PHYSICS (HINGLISH) of Class 12