Complete Solutions to Example of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| DC PANDEY | Example |
| Number Of Questions | 71 |
| Academic Year | 2023-24 |
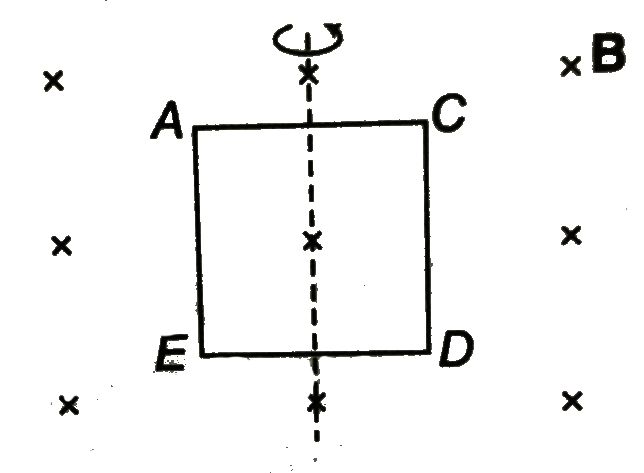
A square loop `ACDE` of area `20 cm^2 ` resistance `5Omega` is rotate in as magnetic field `B=2T` through `180^@` (a) in `0.01S` and (b) in `0.02 s`
Find the magnitudes of averasge values of e i and `/_\q` in both the cases.
View SolutionA coil consists of `200` turns of wire having a total reistance of `2.0Omega`. Each turn is a square of side `18cm,` and a uniform magnetic field directed perpendicular to the plane of the coil is turned on. If the field changes linearly from `0` to `0.5t` in `0.80s`, what is the magnitude of induced emf and current in the coil while the field is changing?
View SolutionThe magnetic flux passing through a metal ring varies with time `t` as: `phi_(B)=3(at^3-bt^2)T-m^2` with `a=2.00s^-3` and `b=6.00s^-2`. The resistance of the ring is `3.0Omega`. Determine the maximum current induced in the ring during te interval from `t=0` to `t=2.0s`.
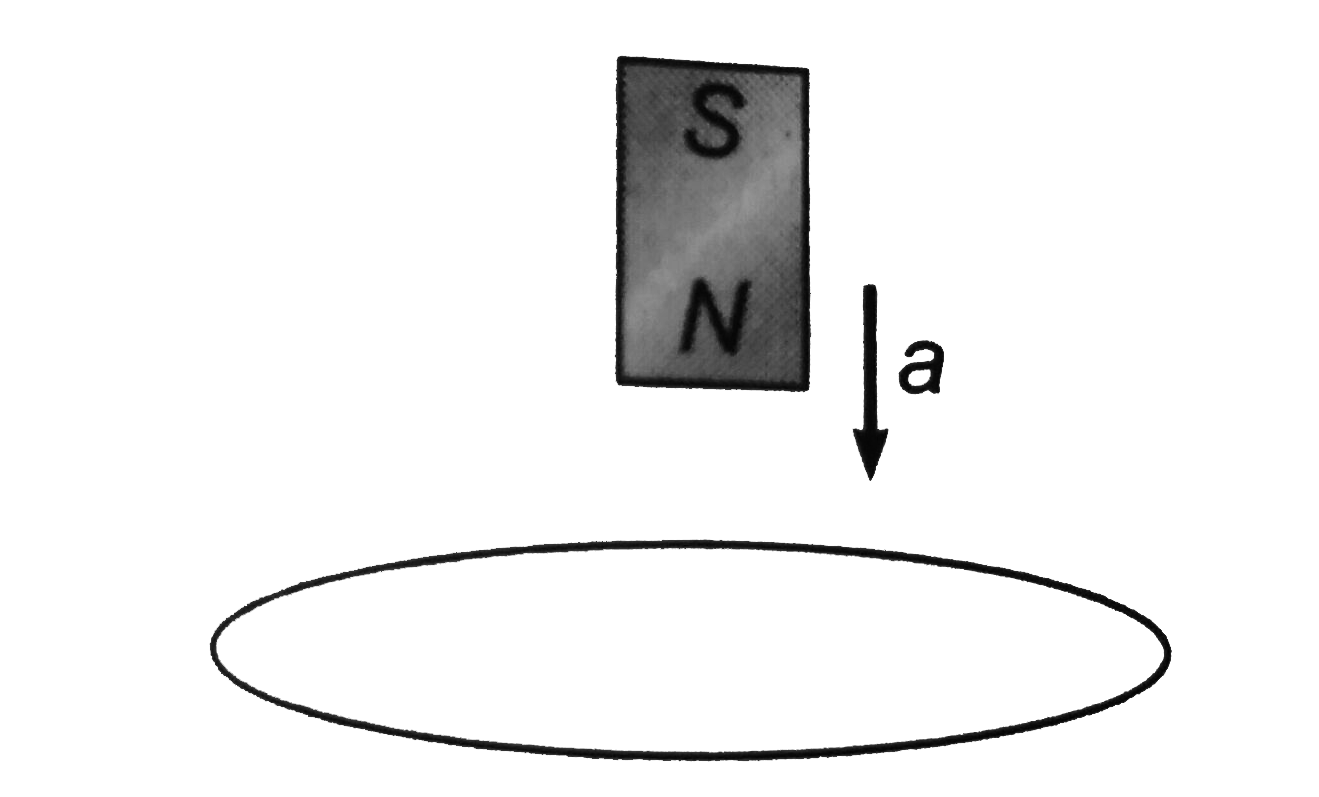
View SolutionA bar magnet is freel falling along the axis of a circular loop as shown in Figure. State whether its acceleration a is equal to greater than or less than the acceleration due to gravity g.
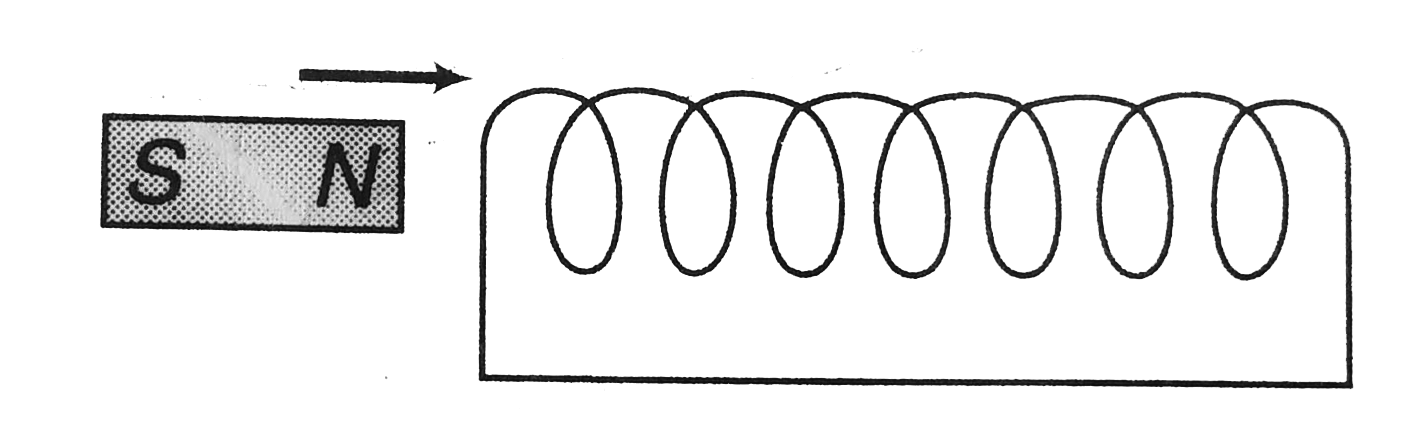
View SolutionA bar magnet is brought near a solenoid as shown in figure. Will the solenoid attract or repel the magnet?
View SolutionA circular loop is placed in magnetic field `B=2t.` Find the direction of induced current produced in the loop.

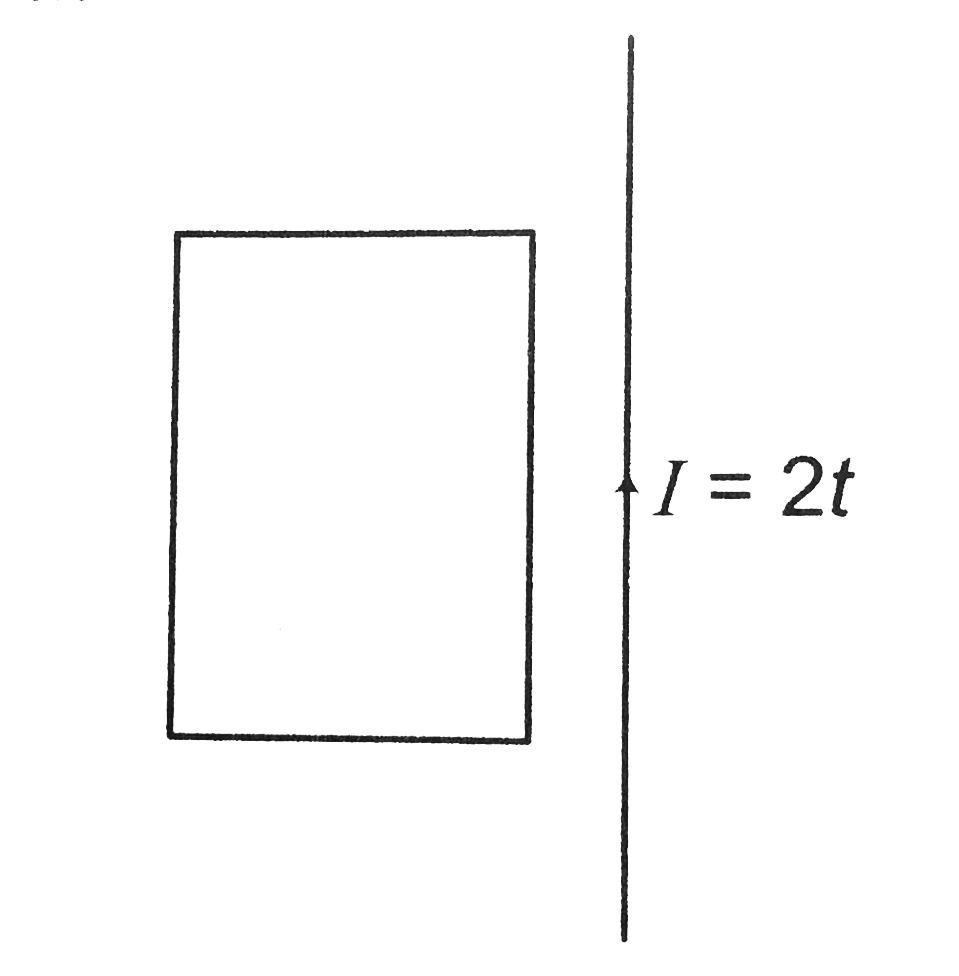
View SolutionA rectangular loop is placed to the left of large current carrying straight wire as shown in Figure. Current varies with time as `I=2t`. Find direction of induced current `I_("in")` in the square loop.
View SolutionA current carrying straight wire passing inside a triangular loop as shown in Figure. The current in the wire is perpendicular to paper inwards. Find the direction of the induced current in the loop if current in the wire is increased.

View SolutionA rectangular loop is placed adjacent toa current carrying straight wire as shown in Figure. If the loop is rotated about an axis passing through one of its sides find the direction of induced current in the loop.

View SolutionTwo loops are facing each other as shown in Figure. State whether the loops will attract each other or repel each other if current `I_1` is increased
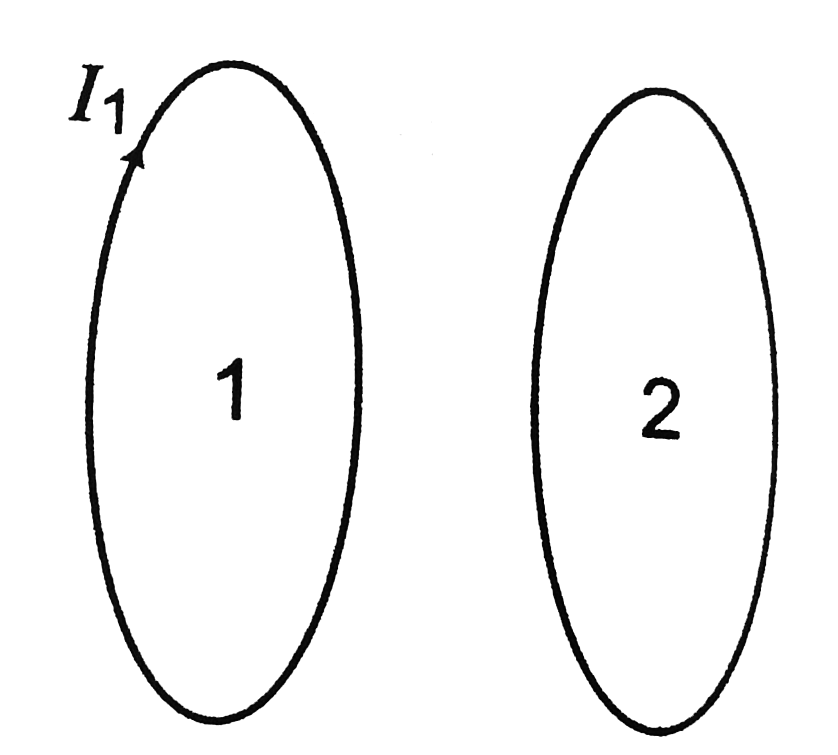
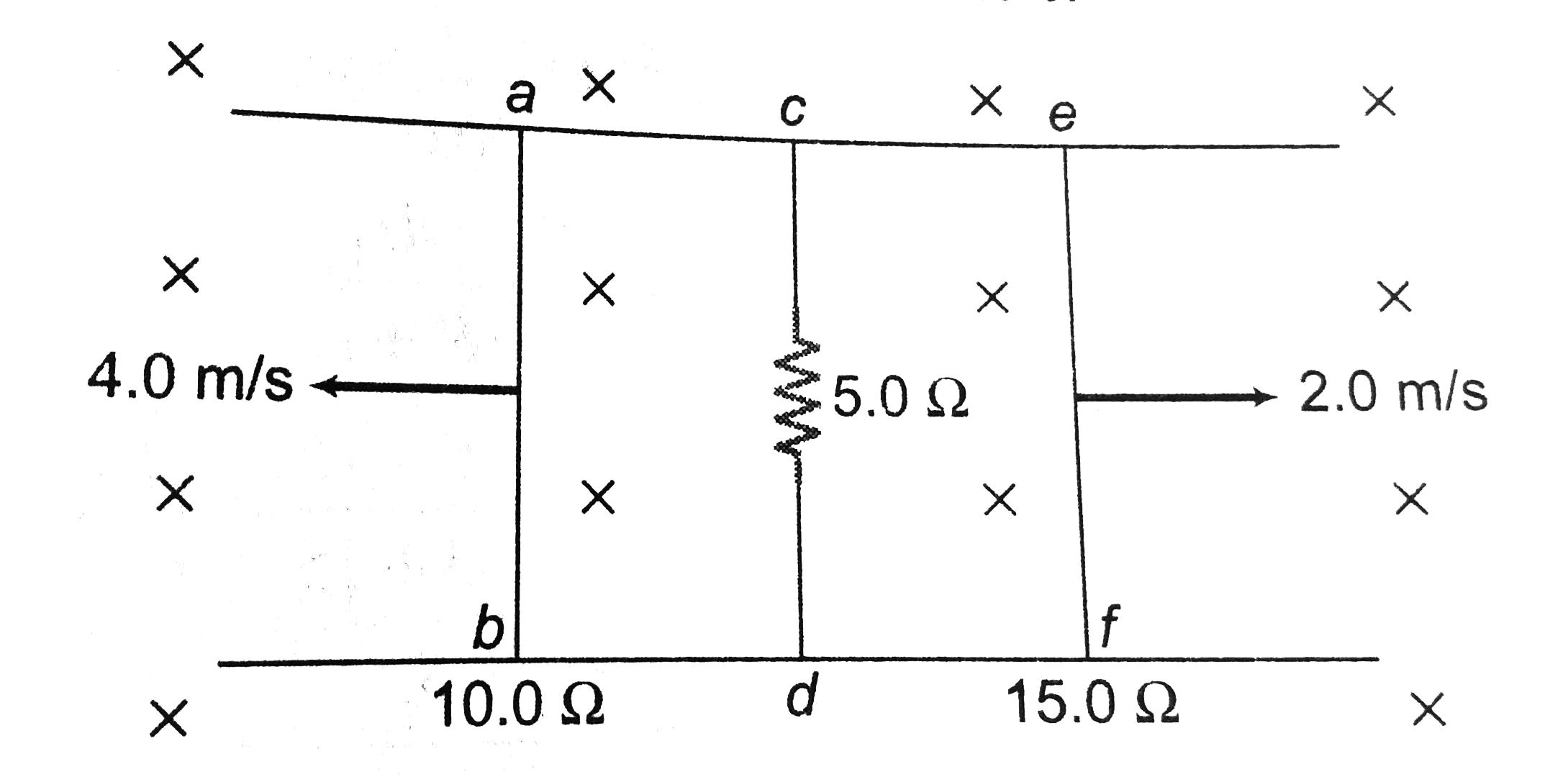
View SolutionTwo parallel rails with negligible resistance are `10.0 cm` apart. The are connected by a `5.0Omega` resistor. The circuit also contains two metal rods having resistances of `10.0Omega` and `15.0Omega` along the rails. The rods are pulled away from the resistor at constant speeds `4.00 m/\s` and `2.00 m//s` respectively. A uniform magnetic field of magnitude `0.01 T` is applied perpendicular to the, plane of the rails. Determine the current in the `5.0Omega` resistor.
View SolutionFigure shows the to views of a rod that can slide without friction. The resistor is `6.0Omega` and a `2.5T` magnetic field is directed perpendicularly downward into the paper. Let `l=1.20m`.

a. Calculate the force `F` required to move the rod to the right at a constant speed of `2.0 m/s`,
b. At what rate is energy deliered to the resistor?
c. Show that this rate is equal to the rate of work done by the applied force.
View SolutionThe inductor shown in figure has inducance `0.54 H` and carries a current in the direction shown thast is decreasing at a uniform rate `(di)/(dt)=0.03A//s`.
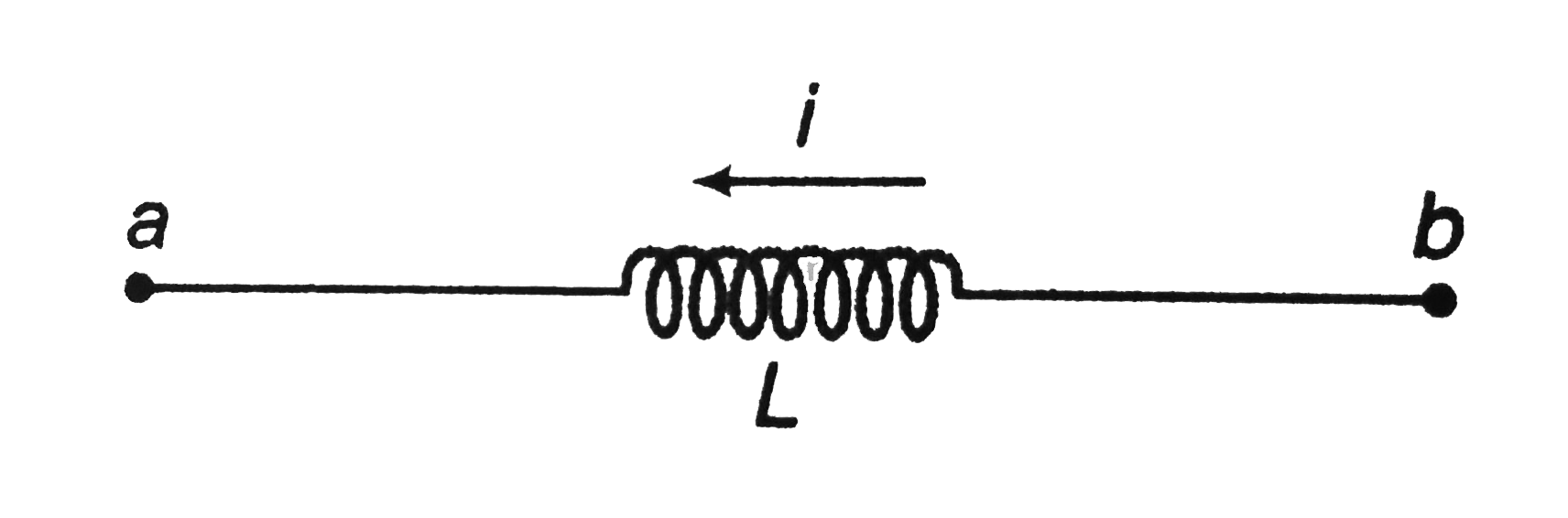
a. Find the self induced emf
b. Which emf of the inductor a ro b is at a higher potential?
View SolutionIn the circuit diagram shown in Figure, `R=10 Omega, L=l5H, E=20v, i=2A`. This current is decreasing at a rate of `-1.0A//s.` Find `V_(ab)` at this instant.

View Solutiona. Calculate the inductance of an air core solenoid containing `300` turns if the length of the solenoid is `25.0cm` and its cross -sectional area is `4.00cm^2`.
b. Calculate the self -induced emf in the solenoid if the current through it is decreasingg at the rate of `50.0A//s`.
View SolutionWhat inductance would be needed to store `1.0 kWh` of energy in a coil carrying a `200 A` current. `(1kWh=3.6xx10^6J)`
View Solutiona. What is the magnetic flux through one turn of a solenoid of self inductance `8.0xx10^-5H` when a current of `3.0 A` flows throgh it? Assume that the solemoid has 1000 turns ans is wound from wire of diameter `1.0 mm`.
b. What is the cross sectional area of the solenoid?
View SolutionA `10 H` inductor carries a current of `20A`. How much ice at `0^@C` could melted by the energy stored in the magnetic field of the inductor? Latent heat of ice is `22.6xx10^I3J//kg`
View SolutionA straight solenoid has 50 turns per cm in primary and total 200 turns in the secondary. The area of cross section of the solenoids is `4cm^2`. Calculate the mutual inductance. Primary is tightly kept in side the secondary.
View SolutionTwo solenoids `A` and `B` spaced close to each other and sharing the same cylindrical axis have `400` and `700` turns, respectively. A current of `3.50A` in coil `A` produced an average flux of `300muT-m^2` through each turn of `A` and `a` flux of `90.0mT-m^2` through each turn of `B`.
a. Calculate the mutual inductance of the two solenoids.
b.What is the self inductance of `A`?
c. What emf is induced in `B` when the current in `A` increases at the rate of `0.5A//s`?
View SolutionA coil of resistance `20Omega` and inductance `0.5H` is switched to `DC200V` supply. Calculate the rate of increase of current
a. at the instant of closing the switch and
b. after one time constant.
c. Find the steady state current in the circuit.
View SolutionA `5H` inductor is placed in series with a `10Omega` resistor. An emf of `5V` being suddenly applied to the combination. Using these values prove the principle of conservation of energy, for time equal to the time constant.
View SolutionA capacitor of capacitance `25muF` is charged to `300V`. It is then connected across a `10mH` inductor. The resistance in the circuit is negligible.
a. Find the frequency of oscillation of the circuit.
b. Find the potential difference across capacitor and magnitude of circuit current `1.2ms` after the inductor and capacitor are connected.
c. Find the magnetic energy and electric energy at `t=0` and `t=1.2ms`.
View SolutionThe magnetic field at all points within the cyllindrical region whose cross section is indicated in the accompanying Figure starts increasing at a constant rate `alpha`. `T//s`. find the magnitud of electric field as a function of `r`, the distance from the geometric centre of the region.

View SolutionA long thin solenoid has `900"tuns"//"metre"` and radius `2.50cm`,. The current in the solenoid is increasing at a uniform rate of `60A//s`. What is the magnitude of the induced electric field at a point?
a. `0.5cm` from the axis of the solenoid.
b. `1.0cm` from the axis of the solenoid.
View SolutionA uniform magnetic field exists in the space `B=B_(1)hati+B_(2)hatj-B_(3)hatk`. Find the magnetic flux through an area S, if the area S is in yz - plane.
View SolutionA long solenoid of radius 4 cm, length 400 cmcarries a current of 3 A. The total number of turns is 100. Assuming ideal solenoid, find the flux passing through a circular surface having centre on axis of solenoid of radius 3 cm and is perpendicular to the axis of solenoid (i) inside and (ii) at the end of solenoid.
View SolutionA long straight wire carrying current I and a square conducting wire loop of side l , at a distance 'a' from current wire as shown in the figure. Both the current wire and loop are in the plane of paper. Find the magnetic flux of current wire, passing through the loop.
View SolutionA coil with an average diameter of 0.02 m is placed perpendicular to a magnetic field of 6000 T. If the induced e.m.f. is 11 V when magnetic field is changed to 1000 T in 4 s, what is the number of turns in the coil ?
View SolutionA coil consists of `200` turns of wire having a total reistance of `2.0Omega`. Each turn is a square of side `18cm,` and a uniform magnetic field directed perpendicular to the plane of the coil is turned on. If the field changes linearly from `0` to `0.5T` in `0.80s`, what is the magnitude of induced emf and current in the coil while the field is changing?
View SolutionThe magnetic flux passing through a metal ring varies with time `t` as: `phi_(B)=3(at^3-bt^2)T-m^2` with `a=2.00s^-3` and `b=6.00s^-2`. The resistance of the ring is `3.0Omega`. Determine the maximum current induced in the ring during te interval from `t=0` to `t=2.0s`.
View SolutionA square loop of side `10 cm` and resistance `0.5 Omega` is placed vertically in the east-west plane. A uniform magnetic field of `0.10 T` is set up across the plane in the north-east direction. The magnetic field is decreased to zero in `0.70 s` at a steady rate. The magnitude of current in this time-interval is.
View SolutionA wire of length l in the form of a square loop lies in a plane normal to a magnetic field `B_(0)`. If this wire is converted into a circular loop in time, then find the average induced emf.
View SolutionSuppose a coil of area `5m^(2)`, resistance `10Omega` and number of turns 200 held perpendicular to a uniform magnetic field of strengh `0.4`T. The coil is now turned through `180^(@)` in time 1 s. What is
(i) average induced emf
(ii) average induced current
(iii) total charge that flows through a given cross-setion of the coil?
View SolutionThrough a long solenoid of diameter `4.1` cm, having 100 turns per cm, a current I = 1A is flowing. At its centre, a 60 turns closely packed coil of diameter `3.1` cm si placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 10 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View SolutionA square loop of edge b having M turns is rotated with a uniform angular velocity `omega` about one of its diagonals which is kept fixed in a horizontal position. A uniform magnetic field `B_(0)` exists in the vertical direction.
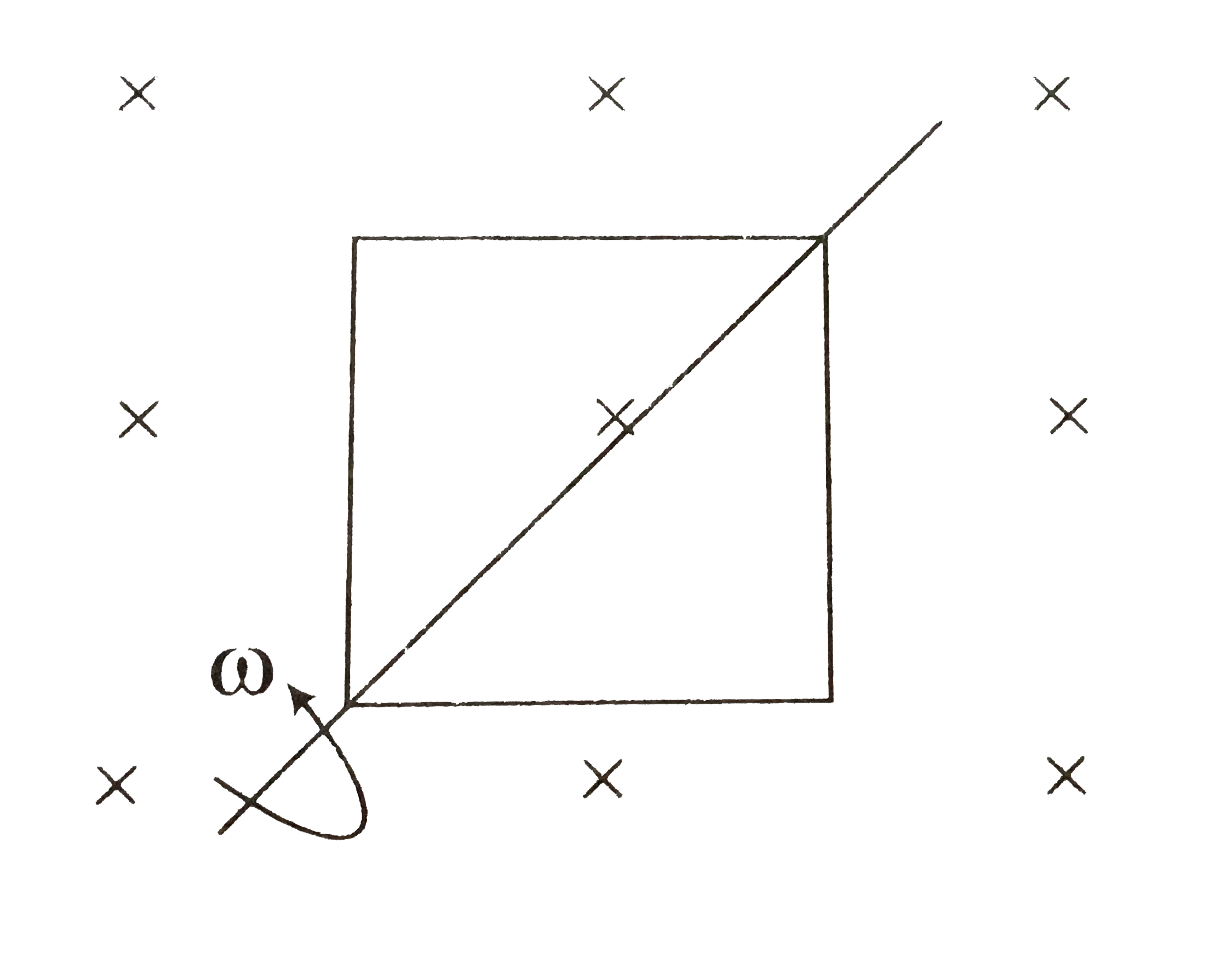
Find (i) the emf induced in the coil as a function of time t.
(ii) the maximum emf induced.
(iii) the average emf induced in the loop over a long period.
(iv) if resistance of loop is R, amount of charge flown in time t = 0 to t = 2T.
(v) heat produced in time t = 0 to t = 2T.
View SolutionA square loop `ACDE` of area `20 cm^2 ` resistance `5Omega` is rotate in as magnetic field `B=2T` through `180^@` (a) in `0.01S` and (b) in `0.02 s`
Find the magnitudes of averasge values of e i and `/_\q` in both the cases.

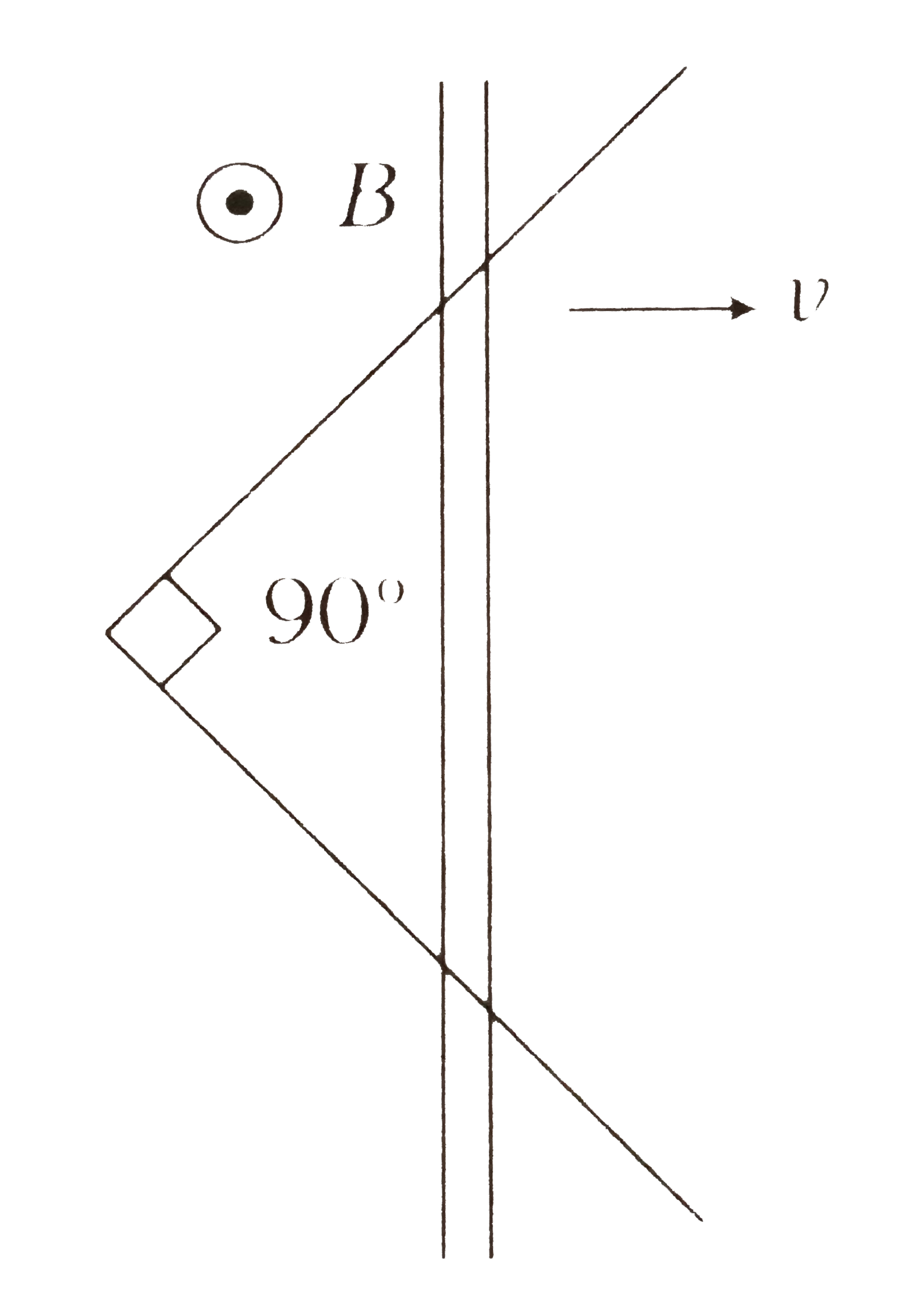
View SolutionThe two conducting rails are placed perpendicular to each other, such that their ends are joined as shown in figure. A conducting bar is now placed over the rails and start moving with constant velocity v starting from the vertex at time t = 0.
(i) The flux through the triangle (isosceles) by the rails and bar at `t=t_(0)`.
(ii) The emf around the triangle at that time.
(iii) In what manner does the emf around the triangle vary with time.
View SolutionA bar magnet is freel falling along the axis of a circular loop as shown in Figure. State whether its acceleration a is equal to greater than or less than the acceleration due to gravity g.

View SolutionA bar magnet is brought near a solenoid as shown in figure. Will the solenoid attract or repel the magnet?

View SolutionA circular loop is placed near a current carrying conductor as shown in figure. Find the direction of induced current, if the current, in the wire is decreasing.

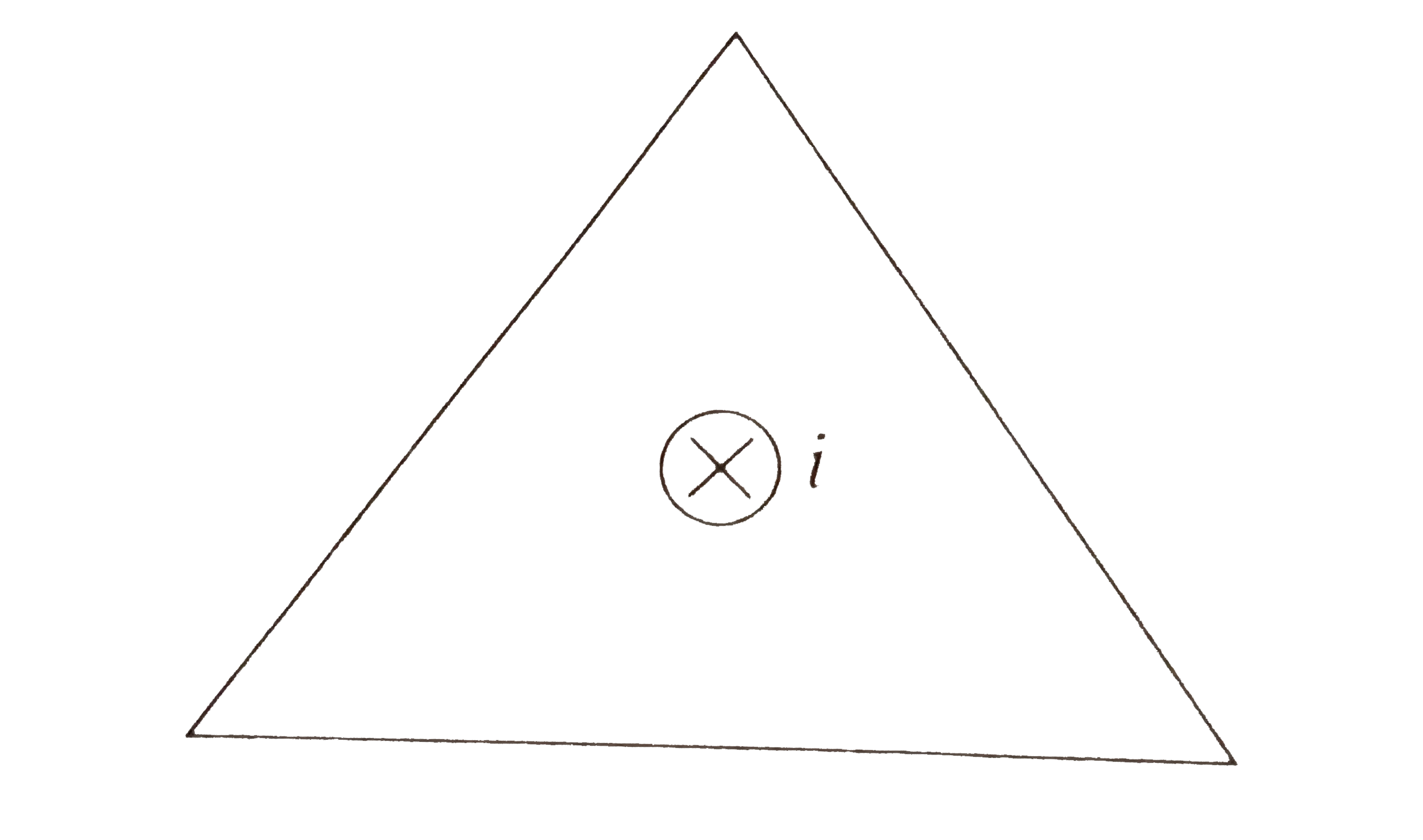
View SolutionA current carrying straight wire passes inside a triangular coil as shown in figure. The current in the wire is perpendicular to paper inwards. Find the direction of the induced current in the loop, if current in the wire is increased.
View SolutionA uniform magnetic field `B=B_(0)that"i"` in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
View SolutionThrough a uniform B field, A small rectangular loop is moving towards left with constant velocity as shown in the figure. Counting of time t begins at the moment, the loop starts entering the field.
Plot the variation of flux through the loop with respect to time. Also, plot the variation of induced emf w.r.t. time t.

View SolutionThrough a conducting coil along its axis, a short bar magnet is rapidly pulled with uniform velocity with, with its north pole entering the coil first. Plot the variation of (i) flux, (ii) induced current and (iii) power dissipated in coil with time.
View SolutionIn a uniform magnetic field, a `pi` shaped metal frame is located perpendicular to the plane of the conductor and varying with time at the rate `(dB//dt)=0.20T//s`. A conducting connector starts moving with an acceleration `a=30cm//s^(2)` along the parallel bars of the frame. The length of the connector is equal to l = 44 cm. Find the emf induced in the loop t = 1 s after the beginning of the motion, if at the moment t = 0, the loop area and the magnetic induction are equal to zero.
View SolutionA conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude `0.4T`. Find the emf induced between the ends of the stick.
View SolutionThe horizontal component of the earth's magnetic field at a place is `4.0xx10^(-4)`T and the dip is `45^(@)`. A metal rod of length 20 cm is placed in the north-south direction and is moved at a constant speed of 5 cm/s towards east. Calculate the emf induced in the rod.
View SolutionA righ of radius 2m translates in its plane with a constant velocity `5m//s`. A uniform magnetic field 0.1 T exists in the space in a direction perpendicualr to the plane of the ring. Consider different pairs of diametrically opposite points on the ring.
(i) Between which pair of points is emf maximum? What is the value of this maximum emf?
(ii) Between which pair of points is the emf maximum? What is the value of this minimum emf?
View SolutionTwo rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude `0.1T` perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
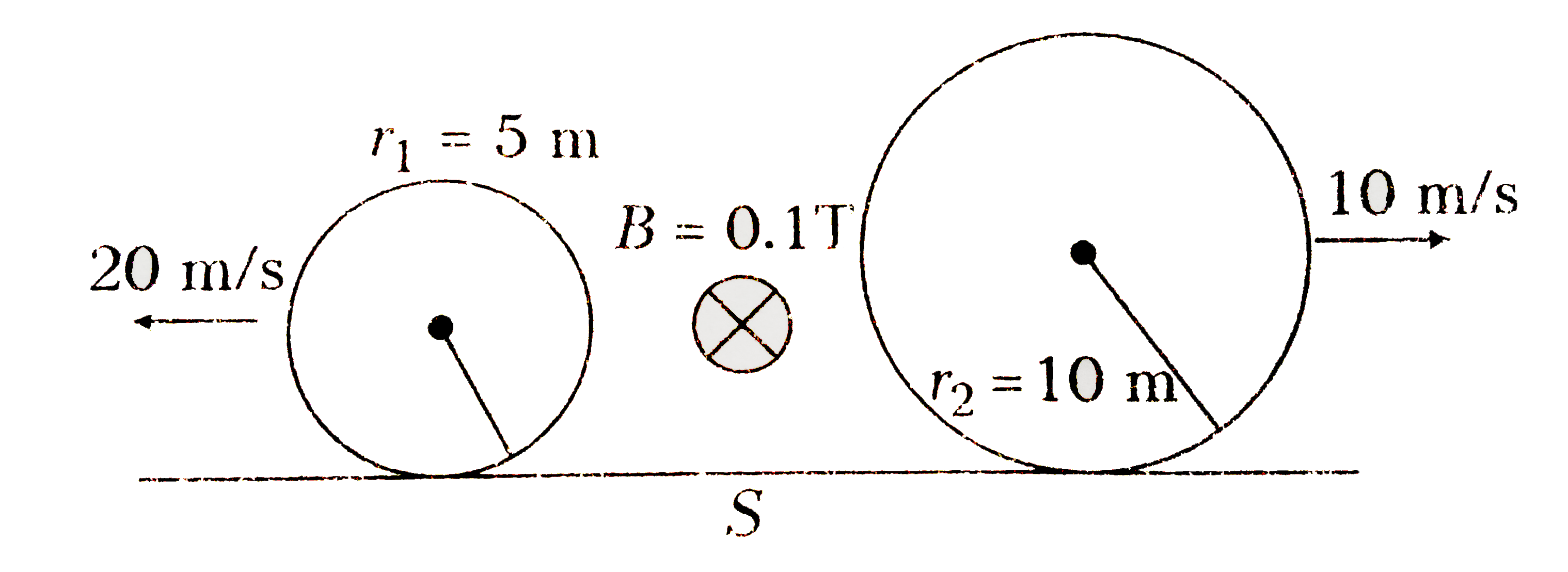
View SolutionA vertical disc of diameter 10 cm makes 20 revolutions per second about a horizontal axis passing through its centre. A uniform magnetic field `10^(-1)` T acts perpendicular to the plane of the disc. Calculate the potential difference between its centre and rim in volts.
View SolutionA square metal wire loop of side 20 cm and resistance `2Omega` is moved with a constant velcoity `v_(0)` in a uniform magnetic field of induction B = 1 `Wb//m^(2)` as shown in the figure. The magnetic field lines are perpendicular to the plane of the loop. The loop is connected to a network of resistance each of value `5Omega`. The resistances of the lead wires BF and AE are negligible. What should be the speed of the loop, so as to have a steady current of 2 mA in the loop? Give the direction of current in the loop.

View SolutionFigure shows the to views of a rod that can slide without friction. The resistor is `6.0Omega` and a `2.5T` magnetic field is directed perpendicularly downward into the paper. Let `l=1.20m`.

a. Calculate the force `F` required to move the rod to the right at a constant speed of `2.0 m/s`,
b. At what rate is energy deliered to the resistor?
c. Show that this rate is equal to the rate of work done by the applied force.
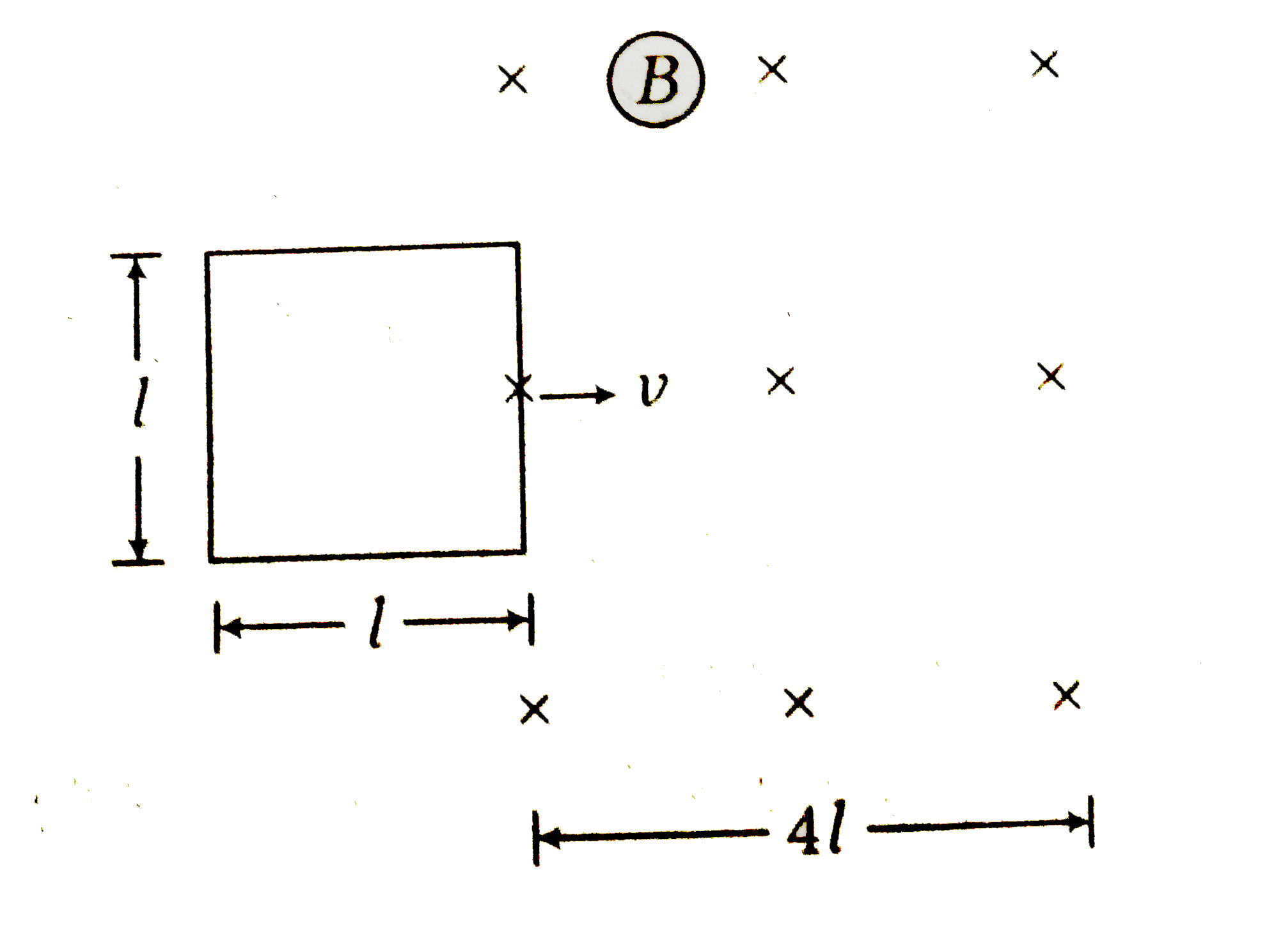
View SolutionA square loop of side l being moved towards right at a constant speed v as shown in figure. The front edge enters the magnetic field B at t = 0. The width of field is 4l. Sketch induced emf versus time graph.
View SolutionTwo parallel rails with negligible resistance are `10.0 cm` apart. The are connected by a `5.0Omega` resistor. The circuit also contains two metal rods having resistances of `10.0Omega` and `15.0Omega` along the rails. The rods are pulled away from the resistor at constant speeds `4.00 m/\s` and `2.00 m//s` respectively. A uniform magnetic field of magnitude `0.01 T` is applied perpendicular to the, plane of the rails. Determine the current in the `5.0Omega` resistor.

View SolutionA uniform magnetic field exists in a circular region of radius R centrad at O. The field is perpendicular to the plane of paper and is strength varies with time as `B=B_(0)t`. Find the induced electric field at a distance r from the centre for (i)`r lt R`, (ii) `r gt R`. Also, plot a graph between `|E|` and r for both the cases.
View SolutionThe cruuent in an ideal, long solenoid is varied at a uniform rate of `0.02A//s`. The solenoid has 1000 turns/s and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.
View SolutionThe inductor shown in figure has inducance `0.54 H` and carries a current in the direction shown thast is decreasing at a uniform rate `(di)/(dt)=0.03A//s`.

a. Find the self induced emf
b. Which emf of the inductor a ro b is at a higher potential?
View SolutionIn the circuit diagram shown in Figure, `R=10 Omega, L=l5H, E=20v, i=2A`. This current is decreasing at a rate of `-1.0A//s.` Find `V_(ab)` at this instant.

View SolutionIn the figure shown `i=10e^(-4t)`A. Find `V_L` and `V_(ab)`

View Solutiona. Calculate the inductance of an air core solenoid containing `300` turns if the length of the solenoid is `25.0cm` and its cross -sectional area is `4.00cm^2`.
b. Calculate the self -induced emf in the solenoid if the current through it is decreasingg at the rate of `50.0A//s`.
View SolutionWhat inductance would be needed to store `1.0 kWh` of energy in a coil carrying a `200 A` current. `(1kWh=3.6xx10^6J)`
View SolutionTwo coils having self-inductances, `L_(1)=5mH` and `L_(2)=1mH`. The current in the coil is increasing of same constant rate at a certain instant and the power supplied to the coils is also same, Find the ratio of
(i) induced voltage
(ii) current
(iii) energy stored in two coils at that instant
View SolutionSuppose a cube of volume `2mm^(3)` is placed at the centre of a circular loop of radius 5 cm carrying current 2A.
Find the magnetic energy stored inside the cube.
View SolutionCalculate the mutual inductance between two coils when a current 2A changes to 6A in and 0.2 s and induces an emf of 20mV in secondary coil.
View SolutionA straight solenoid has 50 turns per cm in primary and total 200 turns in the secondary. The area of cross section of the solenoids is `4cm^2`. Calculate the mutual inductance. Primary is tightly kept in side the secondary.
View SolutionFind the current through the battery
(i) just after the switch is closed.
(ii) long after the switch has been closed.
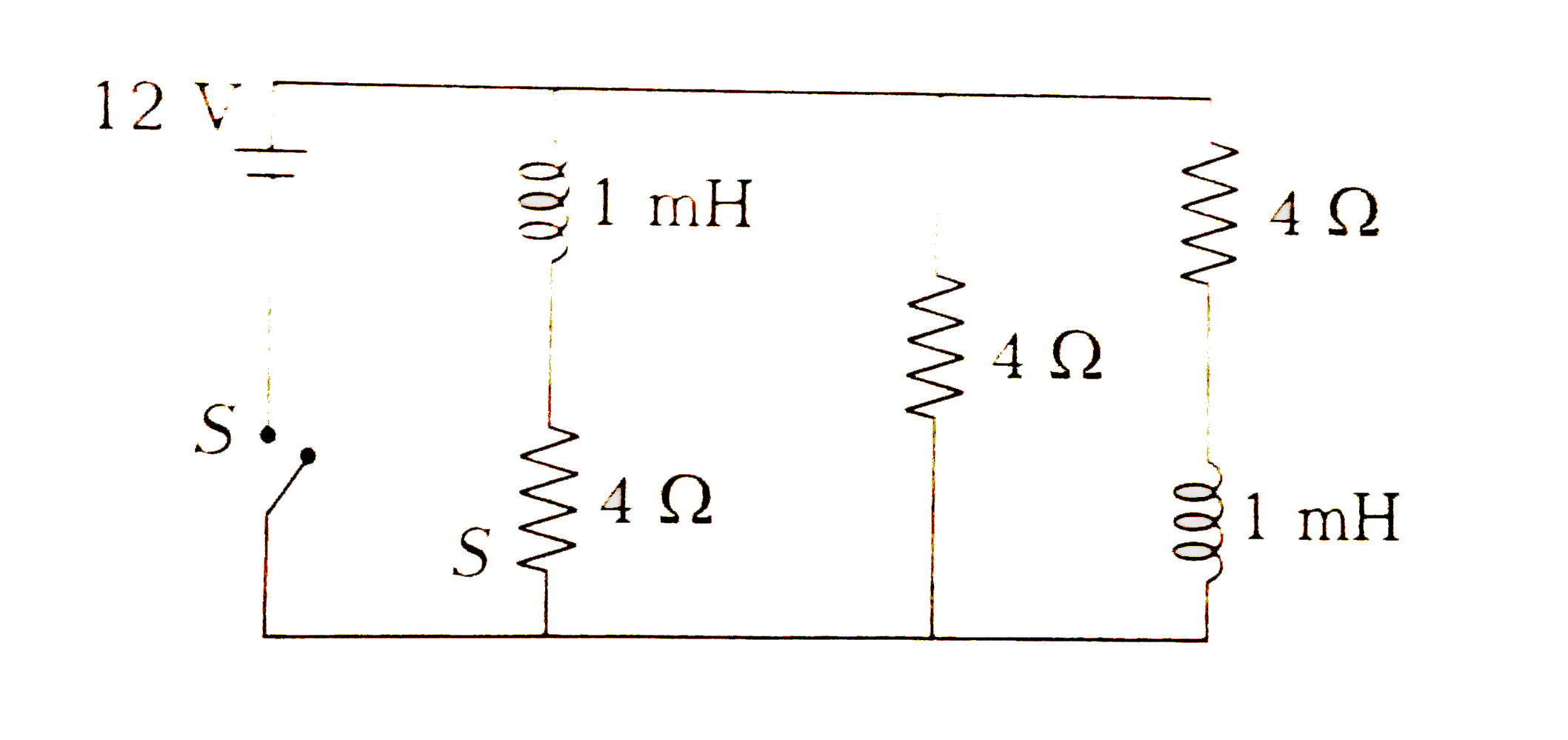
View SolutionA coil of resistance `20Omega` and inductance `0.5H` is switched to `DC200V` supply. Calculate the rate of increase of current
a. at the instant of closing the switch and
b. after one time constant.
c. Find the steady state current in the circuit.
View SolutionSelf - inductance `0.8xx10^(-4)`H of a uniformly wound solenoid, having resistance 3 `Omega` is broken up into two indentical coils. Those coils are connected in series across a 6 V battery of negligible resistance. Find time constant and steady state current.
View Solution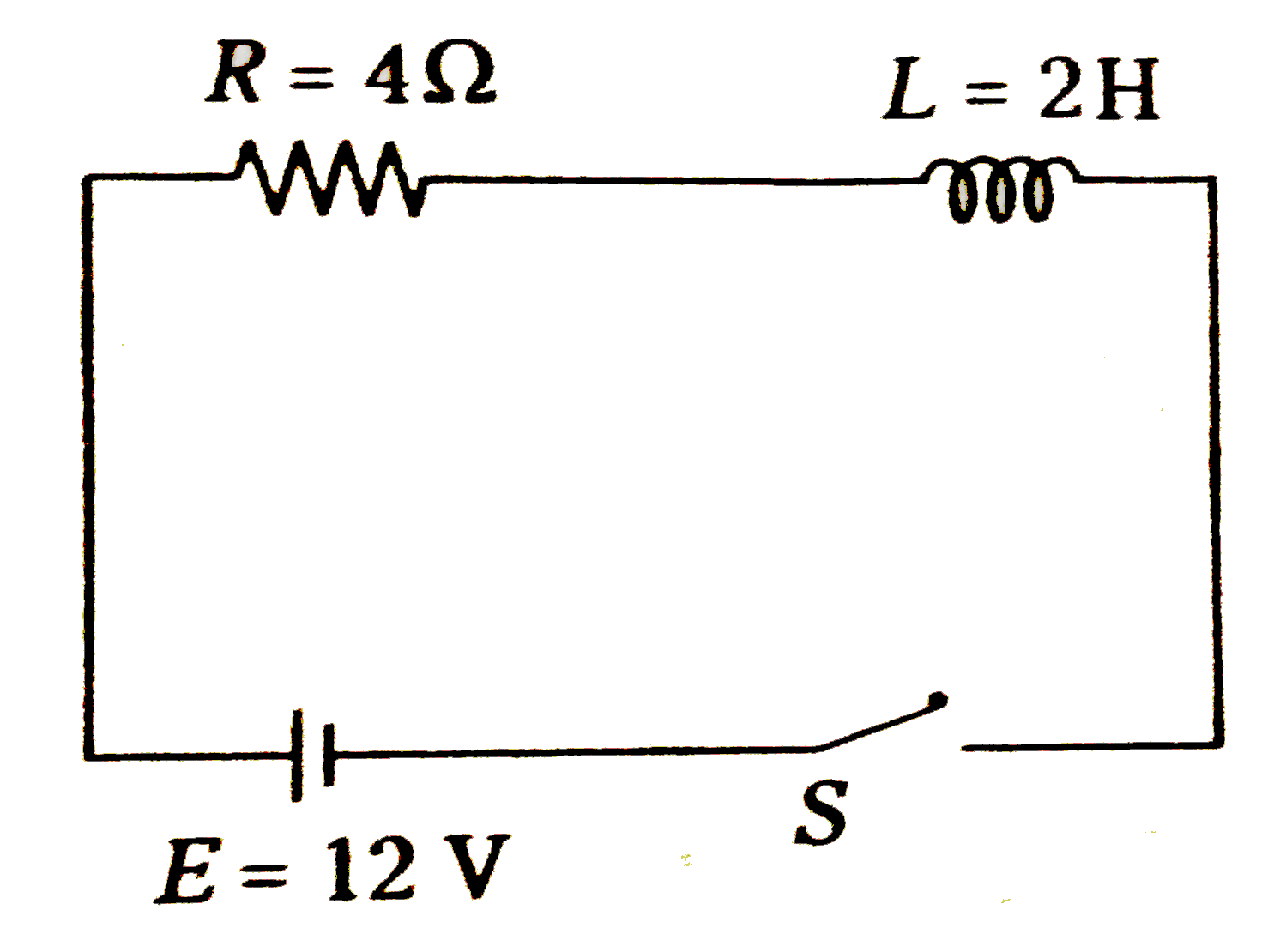
At t = 0, switch S is closed, calculate
(i) initial rate of increase of current, i.e., `(di)/(dt)"at t"=0`.
(ii) `(di)/(dt)` at time when current in the circuit is `0.5A`.
(iii) Current at t = `0.6` s.
(iv) rate at which energy of magnetic field is increasing, rate of heat produced in resistance and rate at which energy is supplied by battery when i = 0.5 A.
(v) energy stored in inductor in steady state.
View Solution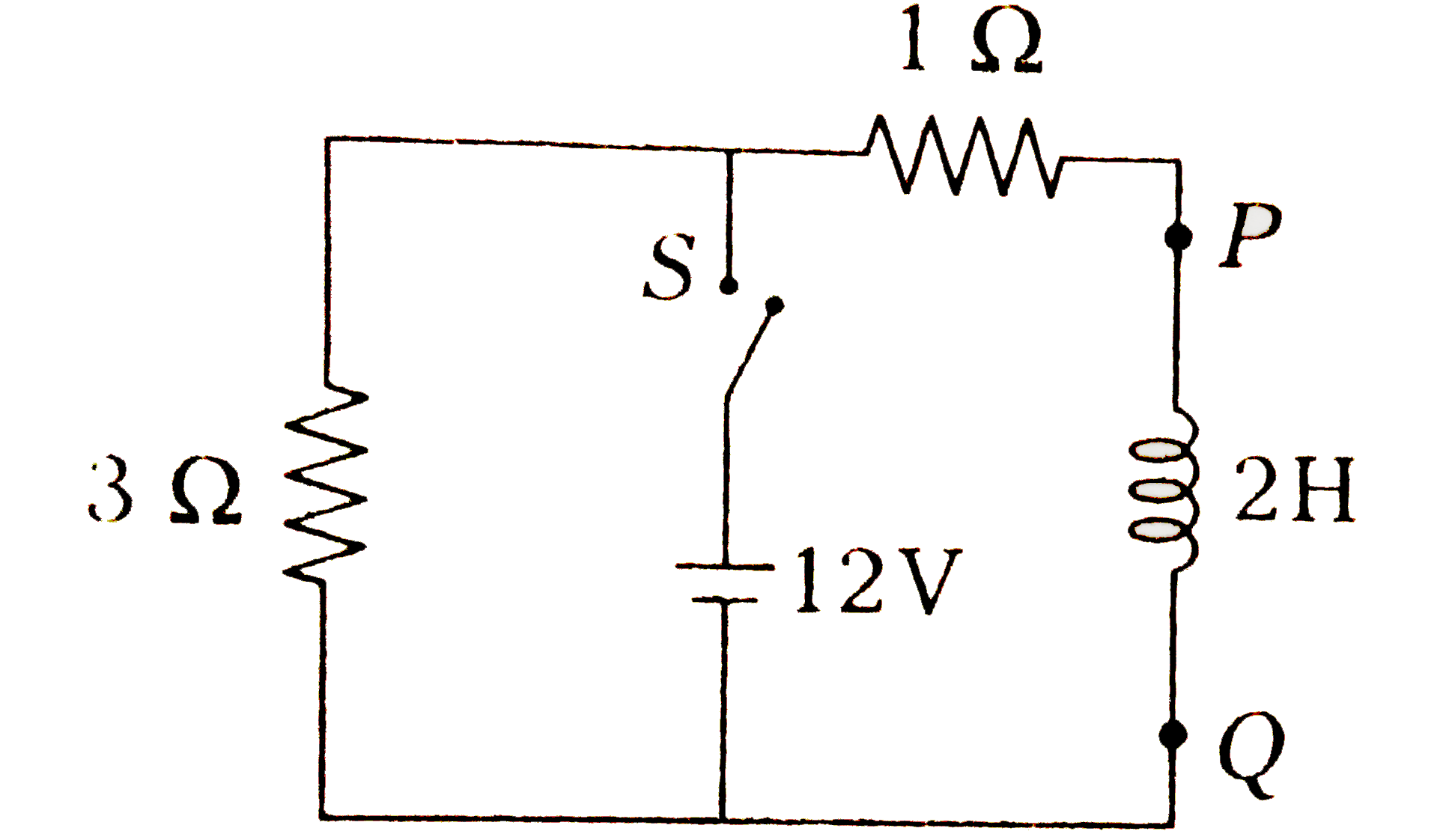
The switch is closed for a long time and then opened at time t = 0. Find the initial voltage across L after t = 0, which end is at higher potential P or Q?
View Solution
Example questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of DC PANDEY PHYSICS (HINGLISH) of Class 12
All Exercises from DC PANDEY Class 12 PHYSICS ELECTROMAGNETIC INDUCTION
- Check point
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Exercise 27.1
- Exercise 27.2
- Exercise 27.3
- Exercise 27.4
- Exercise 27.5
- Exercise 27.6
- Exercise 27.7
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Medical entrance special format questions
- Medical entrances gallery
- Miscellaneous Examples
- Objective Questions
- SUBJECTIVE TYPE
- Taking it together