Complete Solutions to All Questions of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| DC PANDEY MASTER PROBLEM PACKAGE | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
An infinite number of particles each of mass `m` are placed on the positive X-axis of `1m, 2m, 4m, 8m,...` from the origin. Find the magnitude of the resultant gravitational force on mass `m` kept at the origin.
View SolutionA body starts from rest from a point distant `r_(0)` from the centre of the earth. It reaches the surface of the earth whose radius is `R`. The velocity acquired by the body is
View SolutionA hollow spherical shell is compressed to half its radius. The gravitational potential at the centre
View SolutionA satellite revolves in the geostationary orbit but in a direction east to west. The time interval between its successive passing about a point on the equator is:
View SolutionTwo point masses of mass `4m` and `m` respectively separated by `d` distance are revolving under mutual force of attraction. Ration of their kinetic energies will be:
View SolutionA planet revolves about the sun in elliptical orbit. The arial velocity `((dA)/(dt))` of the planet is `4.0xx10^(16) m^(2)//s`. The least distance between planet and the sun is `2xx10^(12) m`. Then the maximum speed of the planet in `km//s` is -
View SolutionBinding energy of a particle on the surface of earth is E. Kinetic energy grater than E is given to this particle. Then total energy of particle will become
View SolutionWhen a satellite in a circular orbit around the earth enters the atmospheric region, it encounters small air resistance to its motion. Then
View SolutionA particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionA particle on earth's surface is given a velocity euqal to its escape velocity. Its total mechanical energy with zero potential energy reference at infinite separation will be:
View SolutionAt what height from the surface of the earth, the total energy of satellite is equal to its potential energy at a height `2R` from the surface of the earth (`R`=radius of earth)
View SolutionTwo earth-satellite are revolving in the same circular orbit round the centre of the earth. They must have the same
View SolutionA hole is drilled from the surface of earth to its centre. A particle is dropped from rest in the surface of earth in terms of its escape velocity on the surface of earth `v_(e)` is :
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side `L`. The work done in increasing the side of the triangle to `2L` is
View SolutionA planet has a mass of eight time the mass of earth and denisity is also equal to eight times a the average density of the earth. If g be the acceleration due to earth's gravity on its surface, then acceleration due to gravity on planet's surface will be
View SolutionThe work done in slowly lifting a body from earth's surface to a height R (radius of earth) is equal to two times the work done in lifting the same body from earth's surface to a height h. Here h is equal to
View SolutionThe magnitude of gravitational potential energy of the moon earth system is U with zero potential energy at infinite separation. The kinetic energy of the moon with respect to the earth is K.
View SolutionThree uniform spheres each of mass `m` and diameter `D` are kept in such a way that each touches the other two, then magnitudes of the gravitational force on any one sphere due to the other two is
View SolutionConsider a thin uniform spherical layer of mass M and radius R. The potential energy of gravitational interaction of matter forming this shell is :
View SolutionFigure shows the variation of energy with the orbit radius r of a satellite in a circular motion. Mark the correct statement.
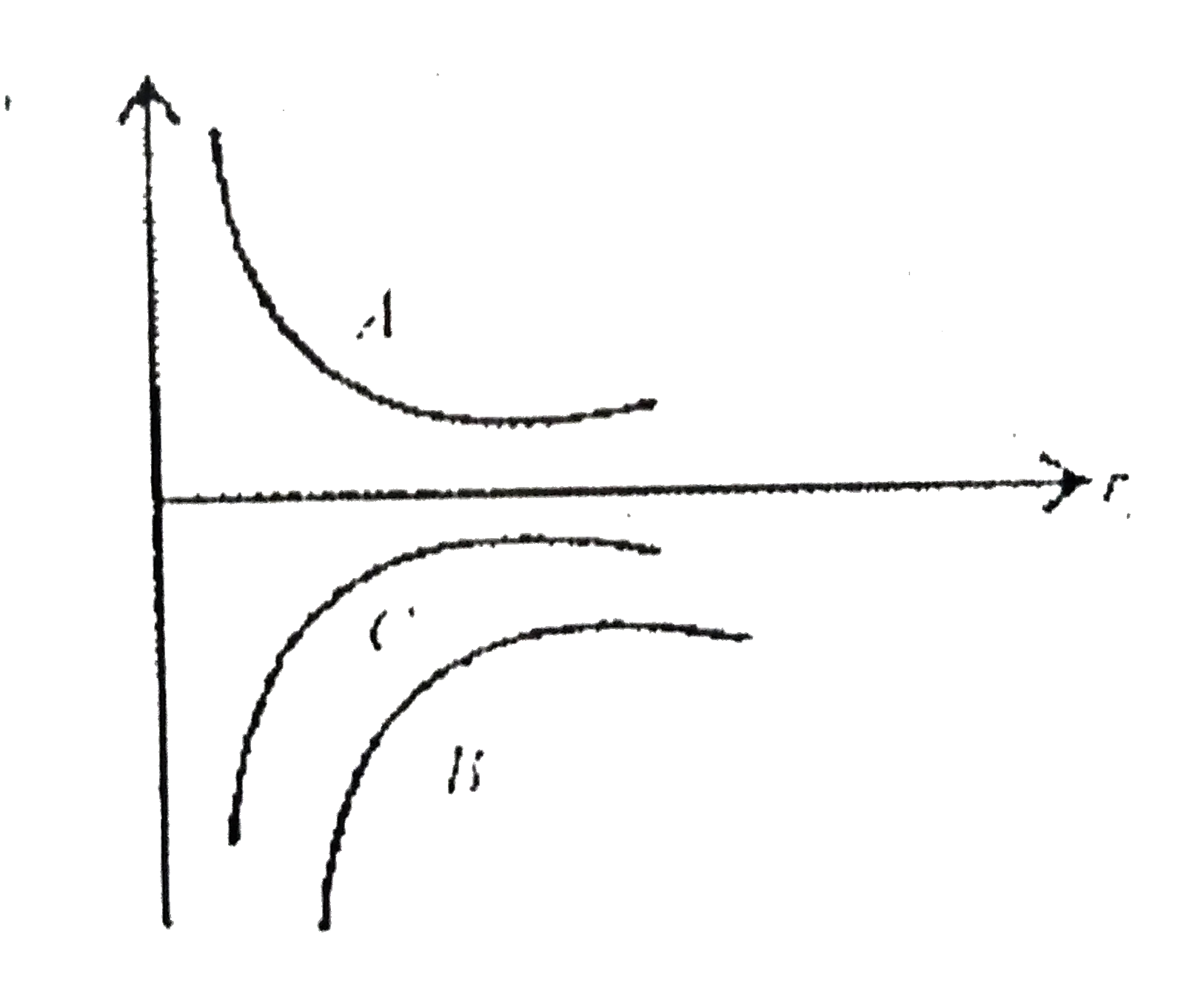
View SolutionIf the radius of the earth were increased by a factor of 2 keeping the mass constant, by what factor would its density have to be changed to keep g the same?
View SolutionA satellite of mass m moves along an elliptical path arouned the earth. The areal velocity of the satellite is proportional to
View SolutionThe period of revolution of an earth satellite close to surface of earth is 90min. The time period of aother satellite in an orbit at a distance of three times the radius of earth from its surface will be
View SolutionThe acceleration due to gravity on the moon is only one sixth that of earth.It the earth and moon are assume to have the same density, the ratio of the radii of moon and earth will be
View SolutionThe acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
View SolutionA geo-stationary stellite orbits around the earth in a circular orbit of radius 36,000km. Then, the time period of a spy stellite orbitting a few hundred km above the earth's surface `(R_(earth) = 6400km)` will approximately be
View SolutionA person brings a mass `2kg` from `A` to `B`. The increase in kinetic energy of mass is `4J` and work done by the person on the mass is `-10J`. The potential difference between `B` and `A` is ......`J//kg`
View SolutionIf the angular velocity of a planet about its own axis is halved, the distance of geostationary satellite of this planet from the centre of the centre of the planet will become
View SolutionA planet of mass `m` is the elliptical orbit about the sun `(mlt ltM_("sun"))` with an orbital period `T`. If `A` be the area of orbit, then its angular momentum would be:
View SolutionIf the radius of the earth were to shrink by one percent its mass remaining the same, the acceleration due to greavity on the earth's surface would
View SolutionIf g is the acceleration due to gravity on the earth's surface, the gain in the potential energy of an object of mass m raised from the surface of the earth to a height equal to the radius R of the earth, is
View SolutionA simple pendulam has time period `T_(1)` when on the earth's surface and `T_(2)` when taken to a height `R` above the earth's surface where `R` is the radius of the earth. The value of `(T_(2))/(T_(1))` is-
View SolutionIf the distance between the earth and the sun were half its present value, the number of days in a year would have been
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionTwo identical spherical masses are kept at some distance. Potential energy when a mass `m` is taken from the surface of one sphere to the other
View SolutionA body of mass `m` is kept at a small height `h` above the ground. If the radius of the earth is R and its mass is M, the potential energy of the body and earth system (with `h=infty` being the reference position) is
View SolutionThe ratio of the energy required to raise a satellite upto a height h above the surface of earth to that the kinetic energy of the satellite into the orbit there is (R=radius of earth)
View SolutionThe gravitational field due to a mass distribution is `E=(A)/(x^(2))` in x-direction. Here, A is a constant, Taking the gravitational potential to be zero at infinity, potential at x is
View SolutionA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
View SolutionThe gravitational field in a in region is given by `vecg = (4hati + vecj) N//kg`. What done by this field is zero when the particle is moved along the line :
View SolutionA thin spherical shell of mass `M` and radius `R` has a small hole. A particle of mass `m` released at its mouth. Then
View SolutionA particle is fired upword with a speed of `20km//s` . The speed with which it will move in interstellar space is
View SolutionTwo bodies of mass `m_(1) and m_(2)` are initially at rest placed infinite distance apart. They are then allowed to move towards each other under mutual gravitational attaction. Show that their relative velocity of approach at separation r betweeen them is
`v=sqrt(2G(m_(1)+m_(2)))/(r)`
View SolutionIf the period of revolution of an artificial satellite just above the earth's surface is T and the density of earth is p, then `pT^(2)` is
View SolutionA satellite is revolving round the earth with orbital speed `v_(0)` if it is imagined to stop suddenly the speed with which it will strike the surface of the earth would be `(v_(e)` - escape speed of a body from earth s surface)
View SolutionThe ratio of the energy required to raise a satellite upto a height h above the surface of earth to that the kinetic energy of the satellite into the orbit there is (R=radius of earth)
View SolutionA spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is

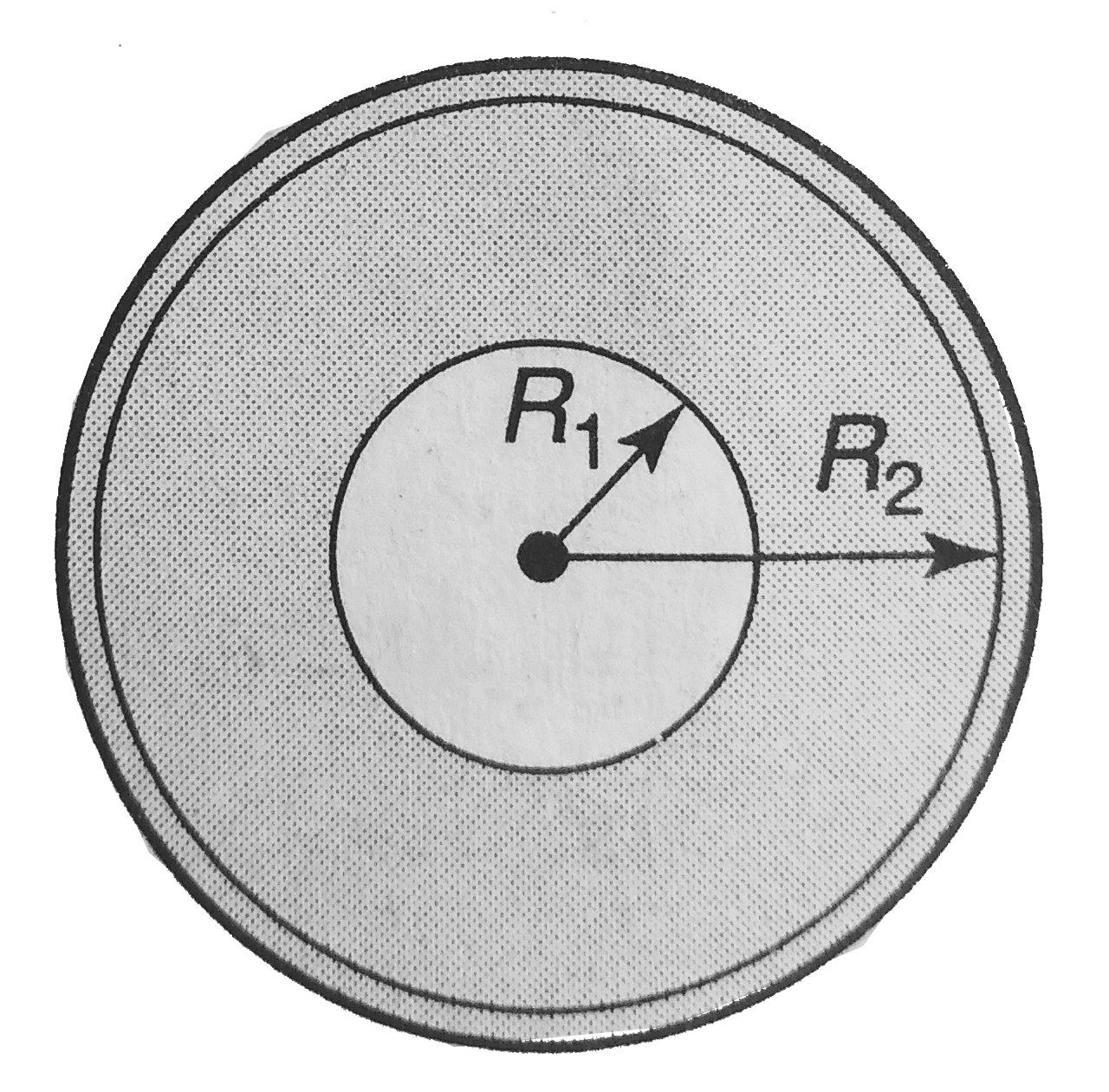
View SolutionA sphare of mass M and ` radiusR_(2) ` has a concentric cavity of radius ` R_(1) ` as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as `(0 lerleoo)` .
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. if the gravitational force of attraction between the planet and the star is proportational to `R^(-5//2)`, then
(a) `T^(2)` is proportional to `R^(2)`
(b) `T^(2)` is proportional to `R^(7//2)`
(c) `T^(2)` is proportional to `R^(3//3)`
(d) `T^(2)` is proportional to `R^(3.75)`.
View SolutionIf G is the uciversal gravitational constant and p is the uniform density of a spherical planet. Then shortest possible period o0f rotation around a planet can be
View SolutionSpeed of a planet in an ellioptical orbit with semimajor axis a about sun of mass M at a distance r from sun is
View SolutionThe magnitude of potential energy per unit mass of the object at the surface of earth is `E`. Then escape velocity of the object is
View SolutionThe radius of a planet is `R`. A satellite revolves around it in a circle of radius `r` with angular velocity `omega_(0)`. The acceleration due to the gravity on planet's surface is
View SolutionThree solid spheres each of mass `m` and radius `R` are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
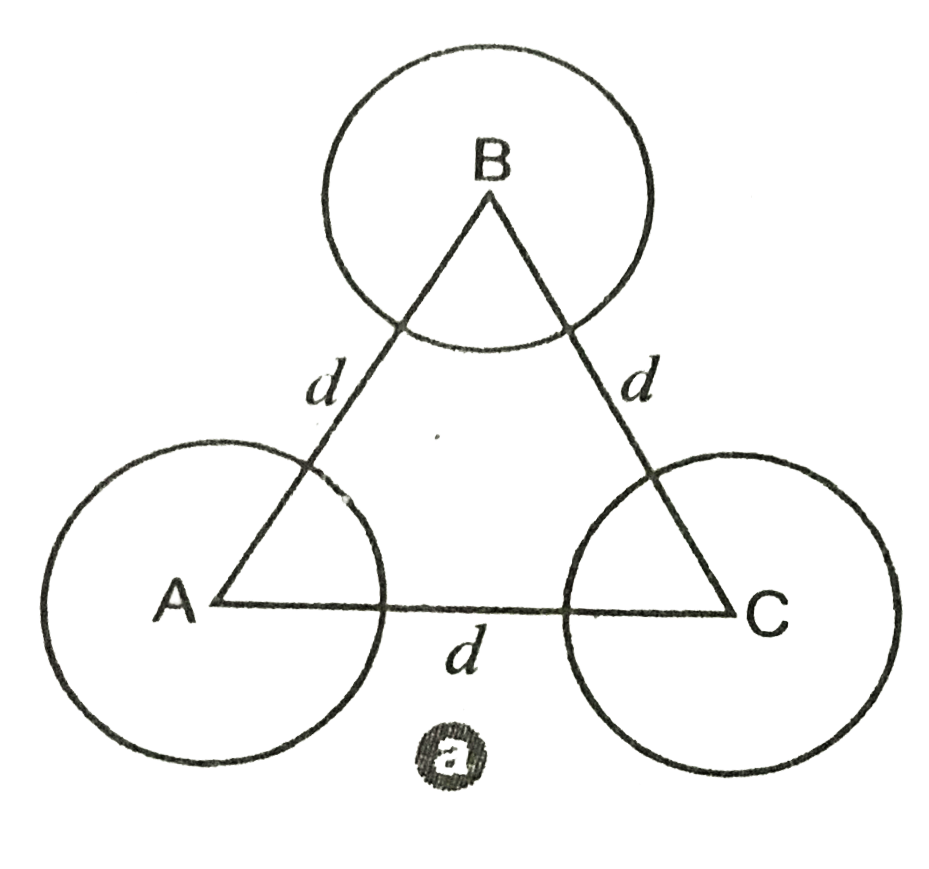
View SolutionThe gravitational force acting on a particle, due to a solid sphere of uniform density and radius `R`, at a distance of `3R` from the centre of the sphere is `F_1.` A spherical hole of radius `(R//2)` is now made in the sphere as shown in diagram. The sphere with hole now exerts a force `F_2` on the same particle. ratio of `F_1` to `F_2` is
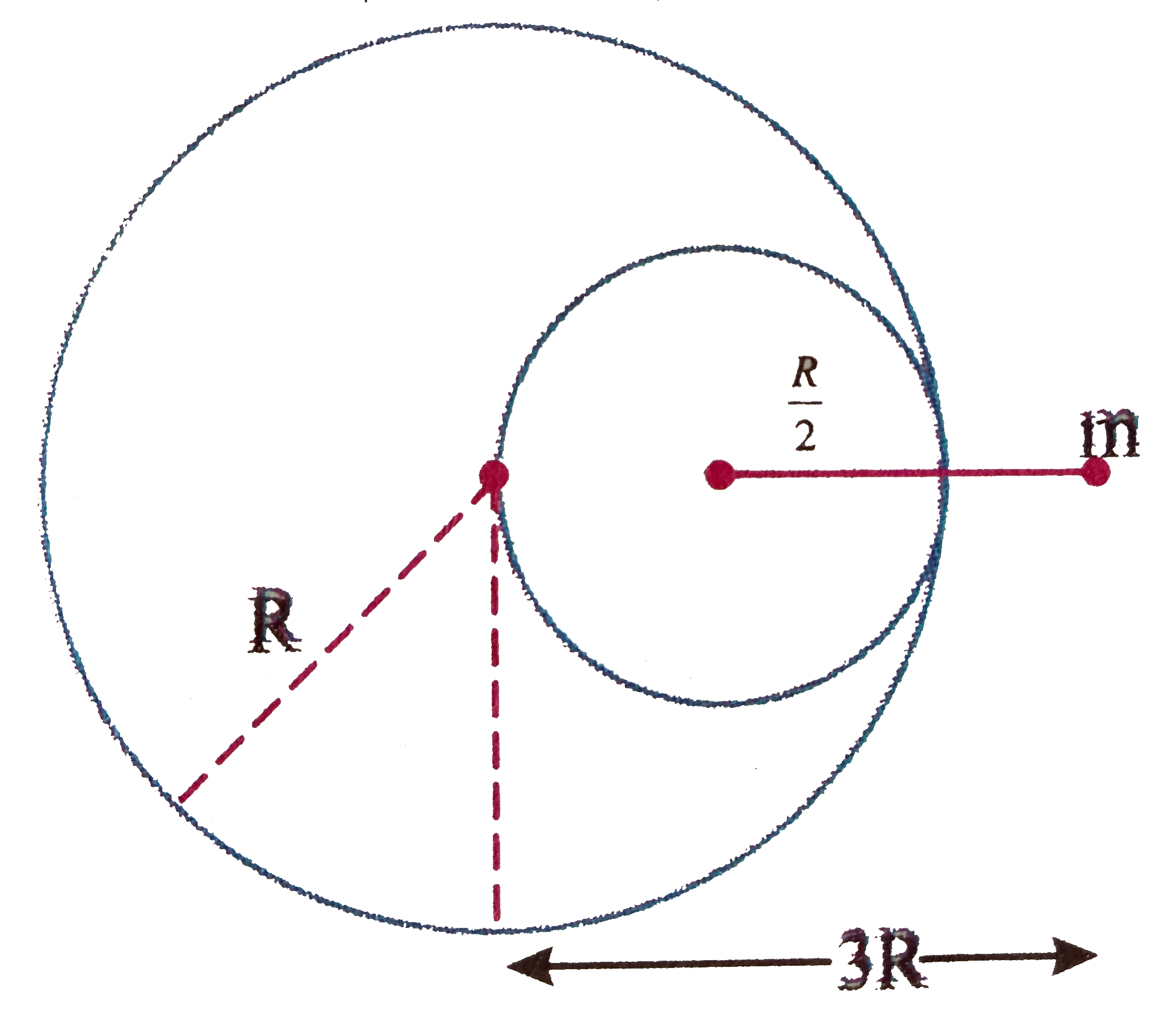
View SolutionA satellite is moving in a circular orbit round the earth with a diameter of orbit 2R. At a certain point a rocket fixed to the satellite is fired such that it increases the velocity of the satellite tangentially. The resulting orbit of the satellite would be
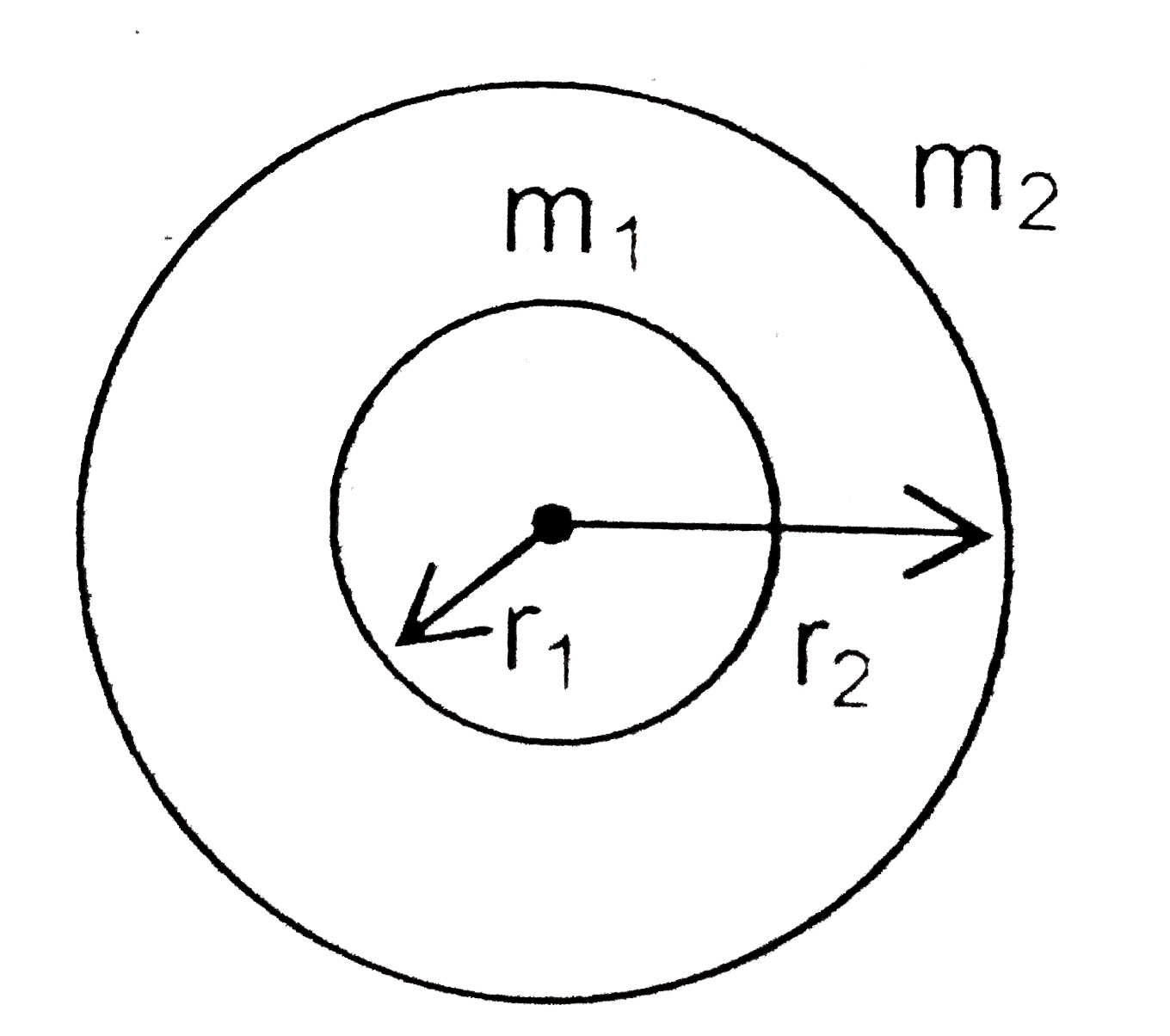
View SolutionTwo concentric spherical sheels are as shown in figure. The `V - r` graph will be as
View SolutionOne ring of radius R and mass m and one solid sphere of same mass m and same radius R are placed with their centres on positive x-axis. We are moving from some finite distance on negative x-axis towards positive x-axis plane of the ring is perpendicular to x-axis. How will the net gravitational field vary with distance moved on x-axis We move only up to surface of solid sphere. O is the origin.
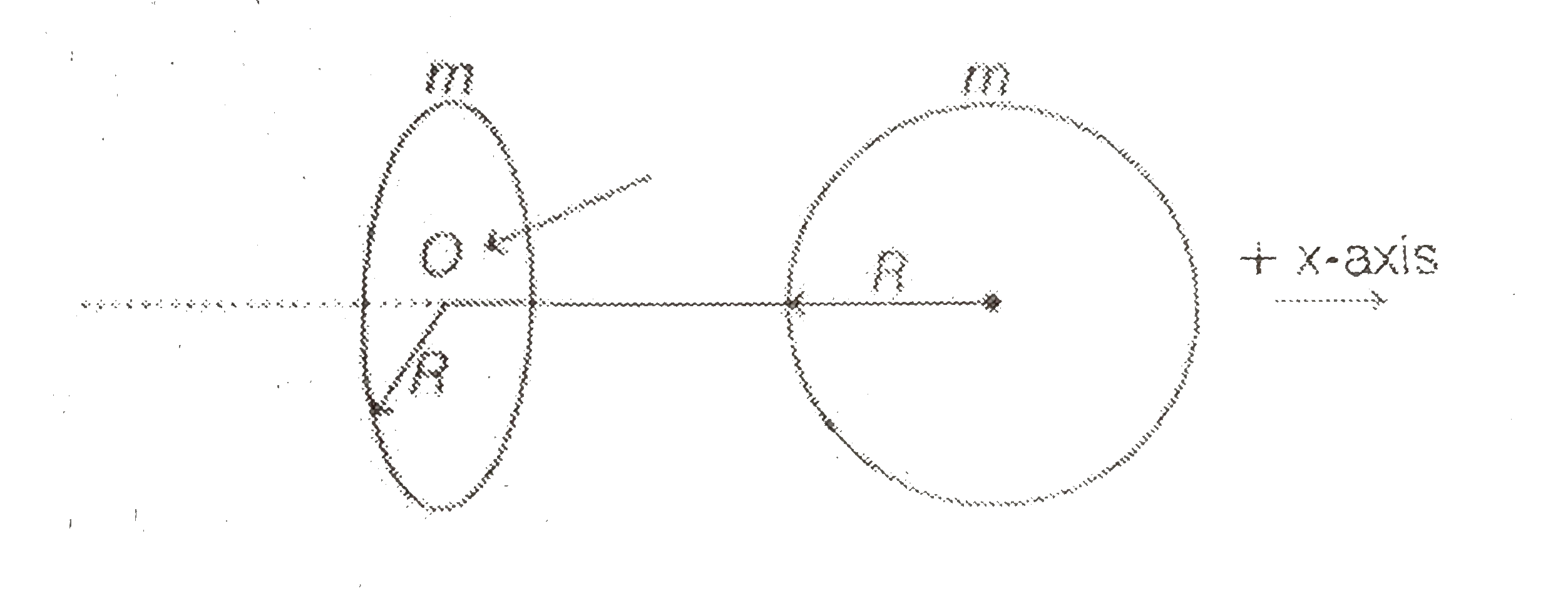
View SolutionA mass is taken from surface to a height h. The change in potential energy in this process is equal to the change in potential energy if it is now taken from that point to infinity. What is the value of h?
View SolutionIf radius of a solid sohere is decreases to half, keeping density of sphere unchanged, the slope of E-r graph inside the sphere will
View SolutionTwo particles each of mass m are revolving in circular orbits of radius `r=5R` in opposite directions with orbital speed `v_(0)` . They collide perfectly inelastically and fall to the ground. The speed of combined mass on triking the ground will be
View Solution_E01_035_Q01.png)
There is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portional is M. What is the gravitational potential at centre?
View SolutionA particle is projected from the surface of earth with velocity equal to its escape velocity , at `45^(@)` with horizontal . What is the angle of its velocity with horizontal at height h = R . (Here horizontal at some point means a line parallel to tangent on earth just below that point . )
View SolutionFour similar particles of mass m are orbiting in a circle of radius r in the same direction and same speed because of their mutual gravitational attractive force as shown in the figure . Speed of a particle is given by
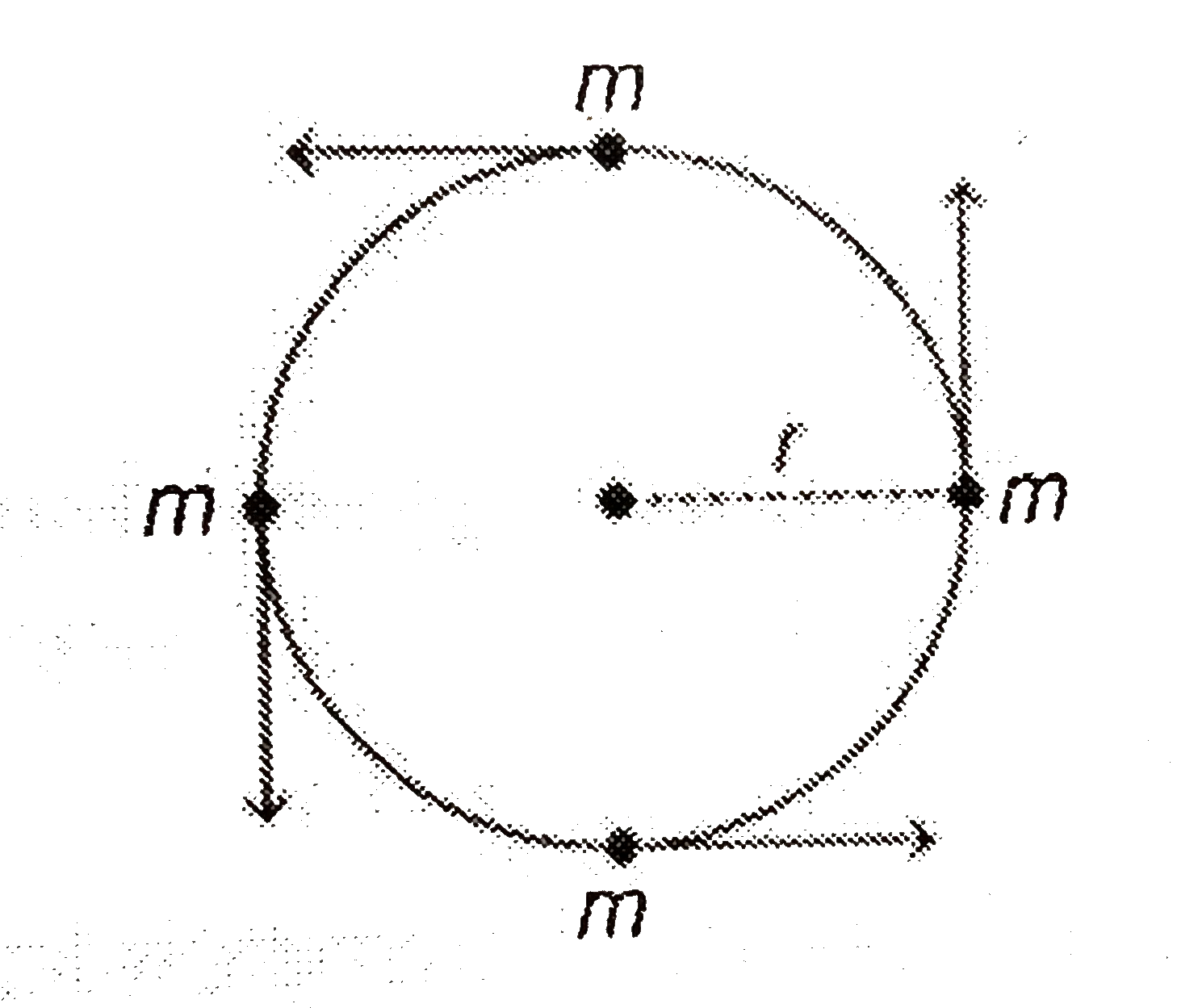
View SolutionThe gravitational potential of two homogeneous spherical shells `A` and `B` of same surface density at their respective centres are in the ratio `3:4`. If the two shells collapse into a single one such that surface charge density remains the same, then the ratio of potential at an internal point of the new shell to shell `A` is equal to
View SolutionA particle of mass `M` is at a distance a from surface of a thin spherical shell of equal mass and having radius `a`.
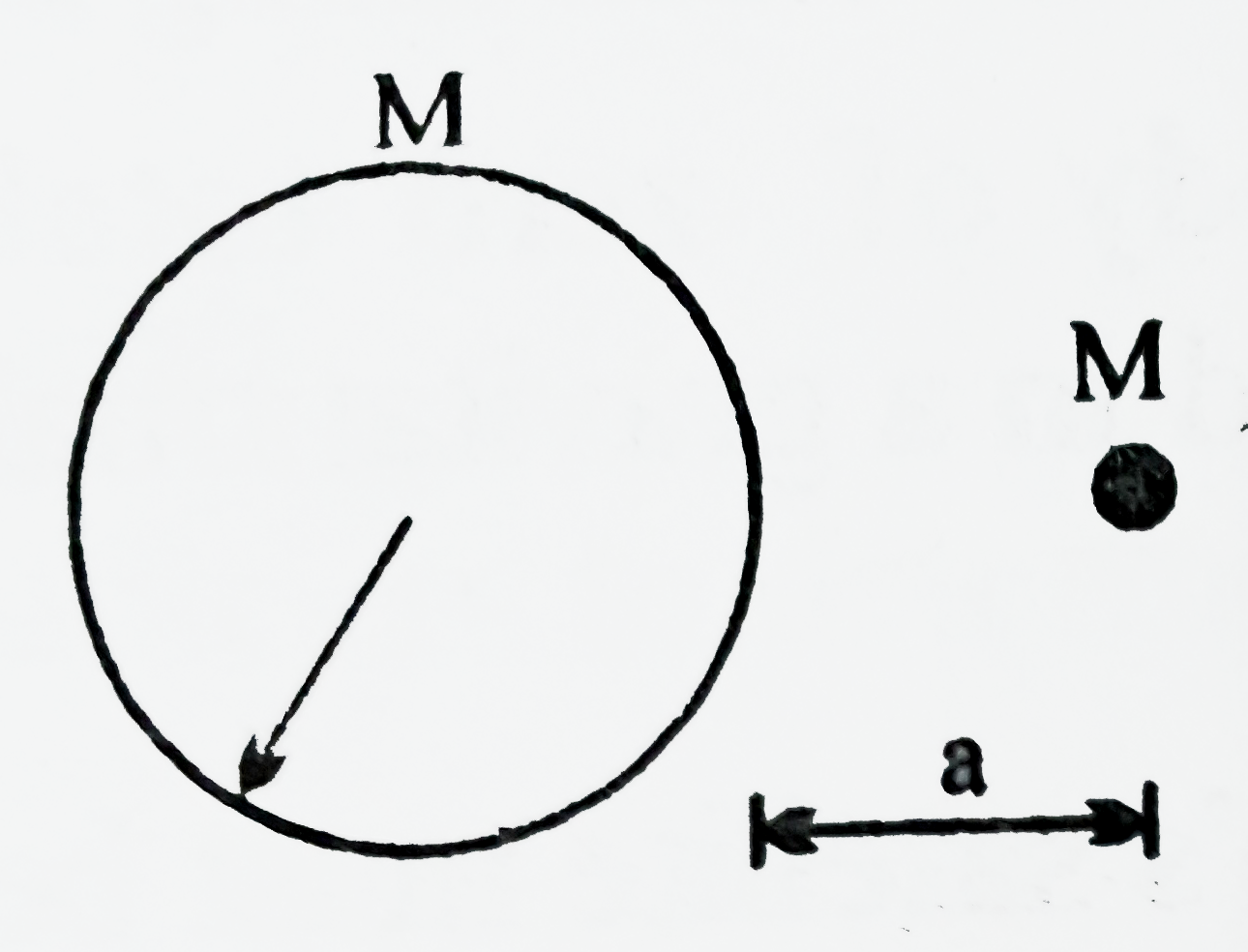
View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
View SolutionFigure (a) shows a ring of mass m and figure (b) shows half portion of the same ring . Gravitational field at point P in figure (b) is `I_(2)` in magnitude and makes an angle `phi` with line . AB. Gravitational field at point P in figure (a) is `I_(1)` in magnitude . The ratio of `(I_(1))/(2 I_(2))` is
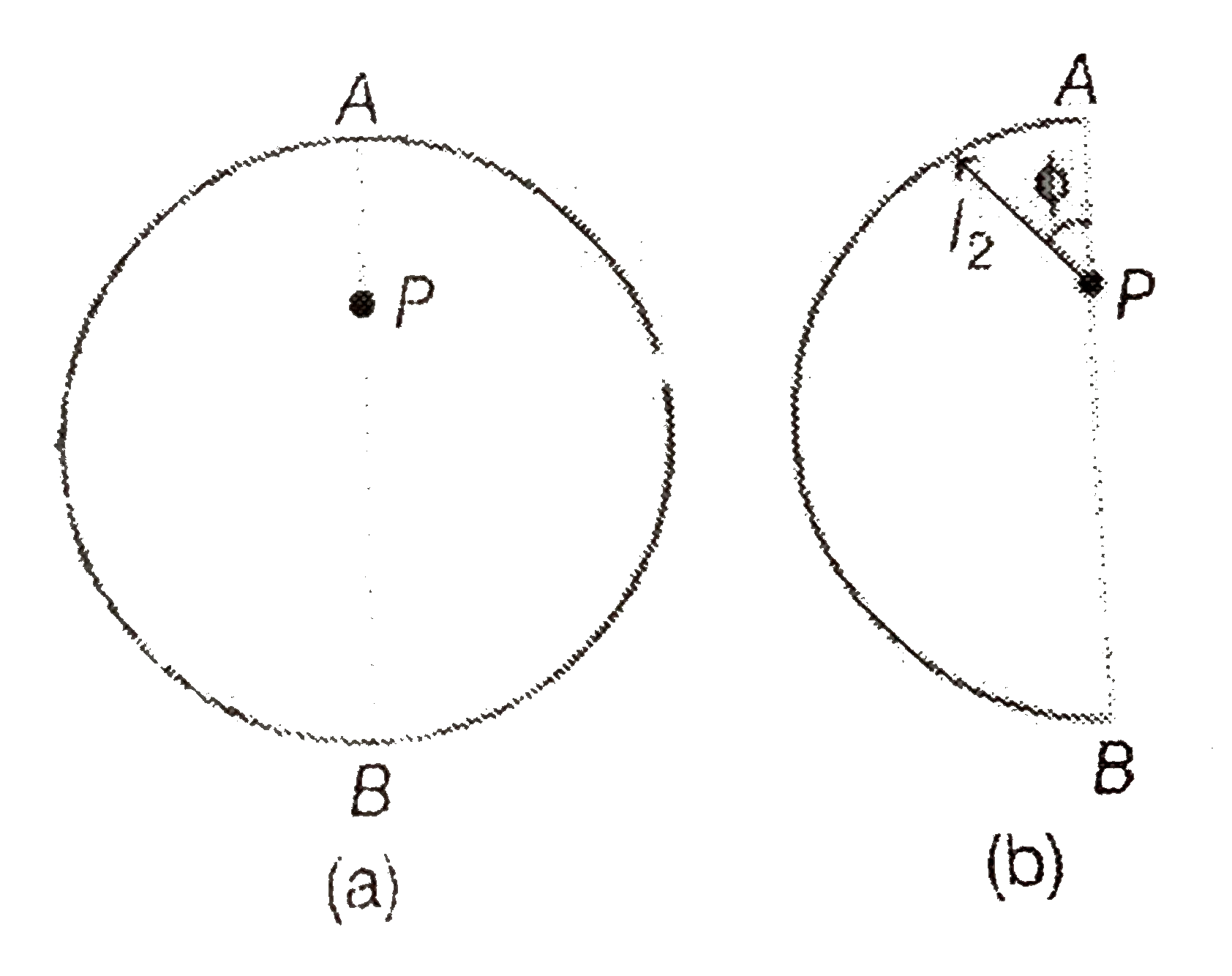
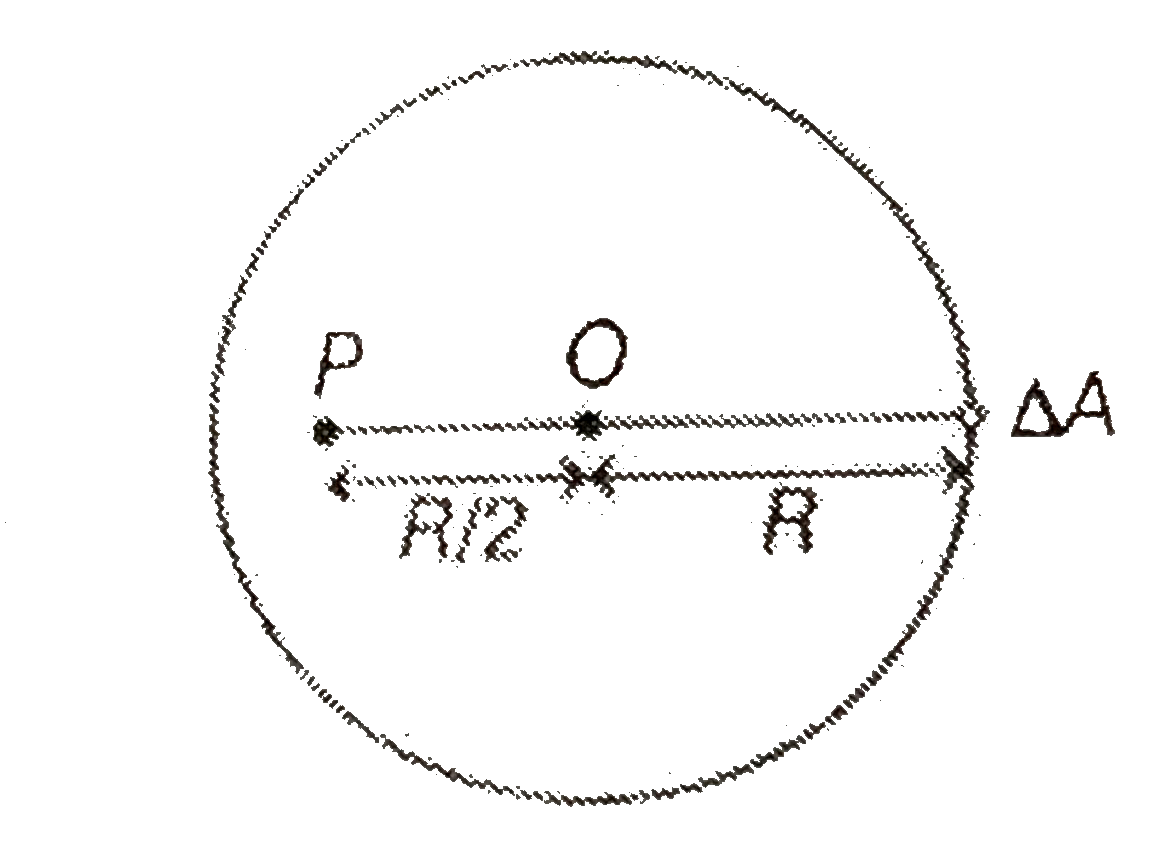
View SolutionA small section of area `DeltaA` is removed from a uniform spherical shell with surface mass density `sigma` and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass .
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass `m` is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass `m` is
View SolutionTwo stars of masses `m_(1)` and `m_(2)` distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionConsider a planet moving in an elliptical orbit around the Sun. The work done on the planet by the gravitational force of the Sun
View SolutionTwo smooth tunnels are dug from one side of earth's surface to the other side, one along a diameter are dropped from one end of each of the tunnels. Both time particles oscillate simple harmonically along the tunnels. Let `T_(1)` and `T_(2)` be the particle along the diameter and along the chord respectively. Then:
View SolutionTwo objectes of mass m and 4m are at rest at and infinite seperation. They move towards each other under mutual gravitational attraction. If G is the universal gravitational constant. Then at seperation r
View SolutionLet V and E be the gravitational potential field. Then select the correct alternative(s) :
View SolutionIn circular orbit of a satellite
View SolutionDue to a solid sphere, magnitude of
View SolutionIn elliptical orbit of a planet
View SolutionAt the surface of earth, potential energy of a particle is U and potential is V.Change in potential energy and potential at height h=R are suppose `DeltaU" and " Delta V`.Then
View Solutionsatellite revolving in circular orbit suppose `V_(0)` is the orbital speed, T its time period, u its potential energy and K the kinetic energy. Now value of G is decreasesd. Then
View SolutionTwo concentric speherical shells are as shown in figure. The magnitude of gravitational potential (V) and field strength (E ) vary with distance ( r) from centre as

View SolutionFor a satellite to apper satationery to an observer on earth.
View SolutionA tunnel is dug along a chord of the earth at a perpendicular distance `R//2` from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with `x` (distance of the particle from the centre) according to
View SolutionIf a body is projected with a speed lesser than escape velocity, then
View SolutionA uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and redius 4a. The centre of the shell falls on the surface of the iner sphere
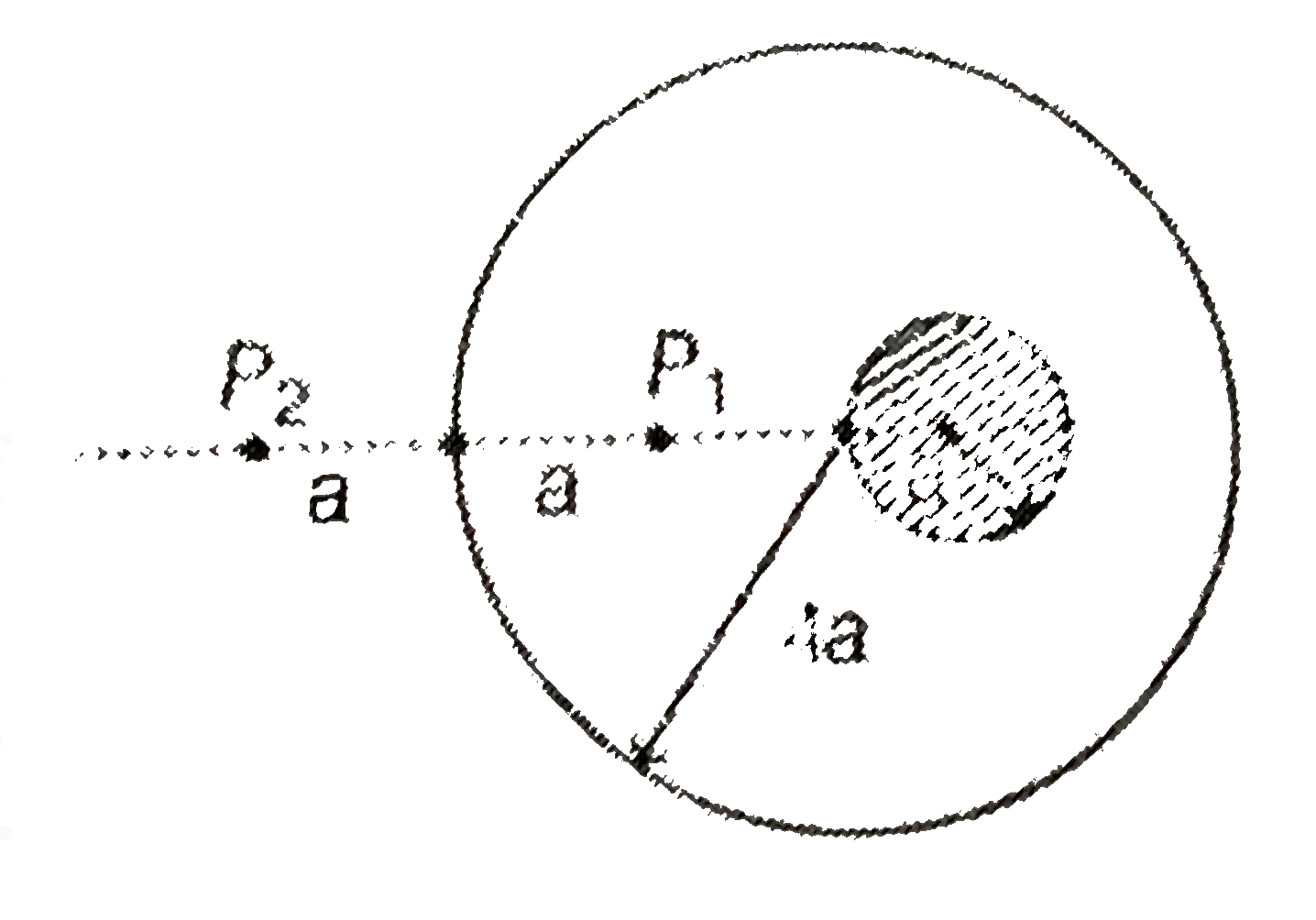
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal to
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle is
View SolutionWhen a particle is projected from the surface of earth its mechanical energy and angular momentum about center of earth at all time are constant.
Q. A particle of mass `m` is projected from the surface of earth with velocity `v_(0)` at angle `theta` with horizontal suppose `h` be the maximum height of particle from surface of earth and v its speed at that point then v is `v_(0)costheta`
View SolutionWhen a particle is projected from the surface of earth its mechanical energy and angular momentum about center of earth at all time are constant.
Q. Maximum height `h` of the particle is
View Solution_S01_036_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass and radius 2R as shown. A small particle of mass m is relased from rest from a height h`(lt lt R)` above the shell. There is a hole in the shell.
Q. In what time will it enter the hole at A
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionThree equal masses each of mass 'm' are placed at the three-corner of an equilateral triangle of side 'a'
In the above system, if two particles are kept fixed and third particle is released, then speed of the particle when it reaches to the mid point of the side connectiong other two masses is
View SolutionAn artificial satellite is moving in circular orbit around the earth with speed equal to half the magnitude of escape velocity from the surface of earth. `R` is the radius of earth and g is acceleration due to gravity at the surface of earth `(R = 6400km)`
Then the distance of satelite from the surface of earth is .
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the surface of earth. R is the radius of earth and g is acceleration due to gravity at the surface of earth. (R=6400 km).
The time period of revolution of satellite in the given orbit is
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth.
(i) Determine the height of the satellite above the earth's surface.
(ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely onto the earth, find the speed with which it hits the surface of the earth.
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass `M` and the other has mass m such that `M =2m` The distance between the centres of the stars is d (d being large compared to the size of either star) .
The period of rotation of the stars about their common centre of mass (in time of d ,m ,G) is .
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass `M` and the other has mass m such that `M =2m` The distance between the centres of the stars is d (d being large compared to the size of either star) .
The ratio of the angular momentum of the two stars about their common centre of mass `(L_(m)//L_(m))` is .
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass `M` and the other has mass m such that `M =2m` The distance between the centres of the stars is d (d being large compared to the size of either star) .
The ratio of kinetic energies of the two stars `(K_(m) //K_(M))` is .
View Solution
All Questions questions and complete solutions for chapter GRAVITATION of DC PANDEY PHYSICS (HINGLISH) of Class 12