If radius of a solid sohere is decreases to half, keeping density of sphere unchanged, the slope of E-r graph inside the sphere will
remain unchanged
become two times
become four times
remain 18 th
The correct Answer is:A
Step by step video, text & image solution for If radius of a solid sohere is decreases to half, keeping density of sphere unchanged, the slope of E-r graph inside the sphere will by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A Sphere of radius R0 carries a volume charge density proportional to the distance (x) from the origin, ρ=αx where α is a positive constant. (a) Calculate the total charge in the sphere of radius R0. (b) The sphere is shaved off so as to reduce its radius. What should be the radius (R) of the remaining sphere so that it contains half the charge of the original sphere? (c) Find the electric field at a point inside the sphere at a distance r lt R. Give your answer for original sphere of radius R0 as well as for the smaller sphere of radius R that was left after shaving off the original sphere.
View SolutionIf r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is (r13+r23)1/3
View Solution
Knowledge Check
If radius of solid sphere is doubled by keeping its mass constant, then
AI1I2=14BI1I2=41CI1I2=32DI1I2=23A spherical charged conductor has σ as the surface density of charge. The electric field on its surface is E. If the radius of the sphere is doubled keeping the surface density of charge unchanged, what will be the electric field on the surface of the new sphere -
AE4BE2CED2EIf the radius of sphere is decreased by 10%, then by what per cent volume of sphere will decrease ?
A30B27.1C29.3D28.5
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
View SolutionThe radius of gyration of a solid sphere of radius R about its tangential is
View SolutionMoment of inertia of a solid sphere of radius R and density p about its diameter is
View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is ρ. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
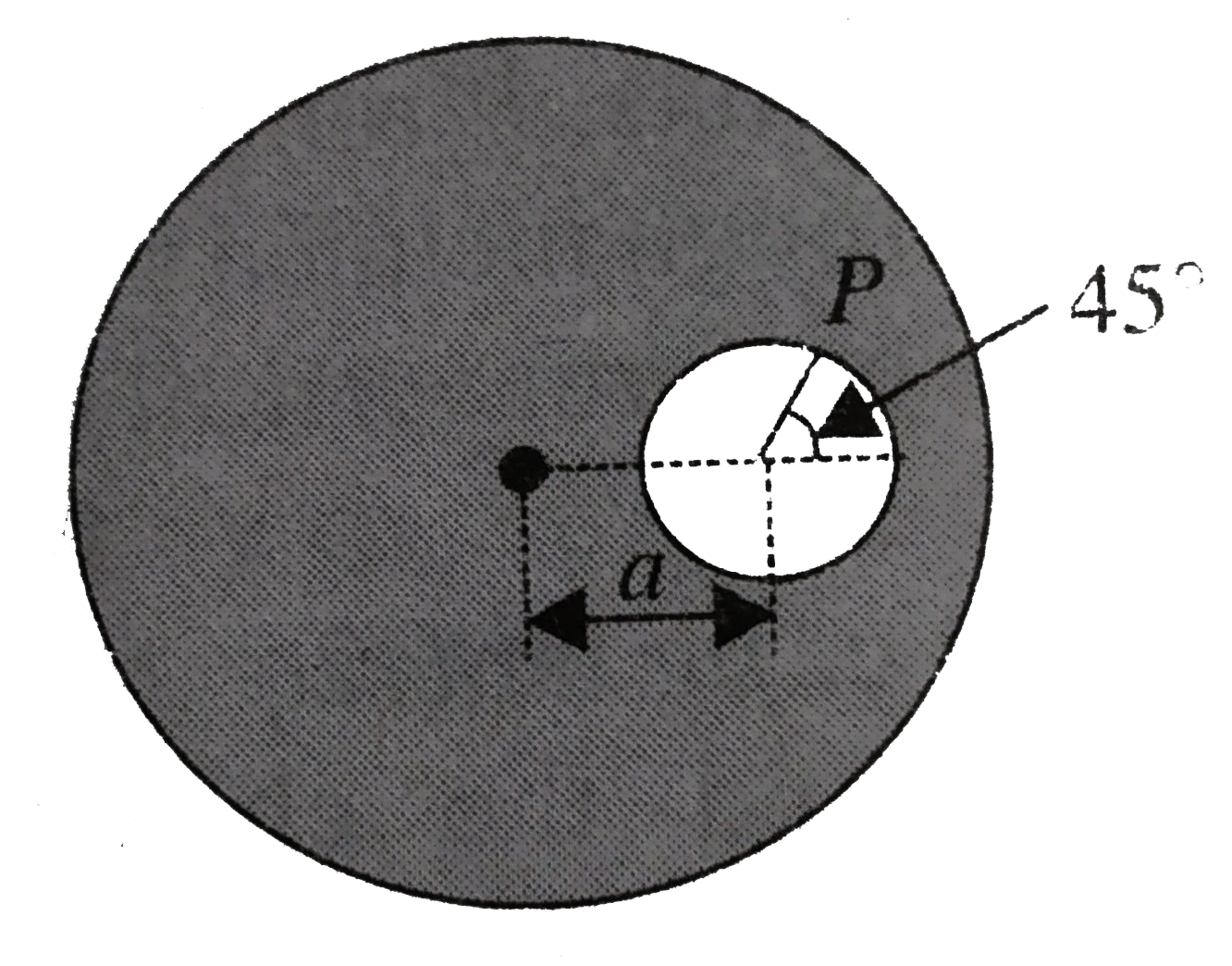
View SolutionLet p(r)=QπR4r be the charge JIR density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at distance z1from the centre of the sphere, the magnitude of electric field is
View Solution
