Complete Solutions to For JEE Advanced E. Integer Type Questions of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| DC PANDEY MASTER PROBLEM PACKAGE | For JEE Advanced E. Integer Type Questions |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
In the Young's double slit experiment, the intensities at two points `P_(1)` and `P_(2)` on the screen are respectively `I_(1)` and `I_(2)` If `P_(1)` is located at the centre of a bright fringe and `P_(2)` is located at a distance equal to a quarter of fringe width from `P_(1)` then `I_(1)/I_(2)` is
View SolutionIn Young's double slit experiment, the two slits acts as coherent sources of equal amplitude A and wavelength `lambda`. In another experiment with the same set up the two slits are of equal amplitude A and wavelength `lambda` but are incoherent. The ratio of the intensity of light at the mid-point of the screen in the first case to that in the second case is
View SolutionTwo waves of same frequency and same amplitude from two monochromatic sources are allowed to superpose at a certain point. If in one case the phase difference is 0 and in other case it is `pi//2` then the ratio of the intensities in the two cases will be
View SolutionAn interference is observed due to two coherent sources separated by a distance `5lambda` along Y-axis, where `lambda` is the wavelength of light A detector D is moved along the positive X -axis The number of point on the X-axis excluding the points x=0 and `x=infty` at which resultant intensity will be maximum are
View SolutionTwo beam of light having intensities I and 4I interfere to produce a fringe pattern on a screen. The phase difference between the beams is `(pi)/(2)` at point A and `pi` at point B. Then the difference between resultant intensities at A and B is : `(2001 , 2M)`
View SolutionIn a Young's experiment, one of the slits is covered with a transparent sheet of thickness `3.6xx10^(-3)cm` due to which position of central fringe shifts to a position originally occupied by 30th fringe. If `lambda=6000 Å`, then find the refractive index of the sheet.
View SolutionOne slit of a double slits experiment is covered by a thin glass plate of refractive index`1.4`and the other by a thin glass plate of refractive index`1.7` .The point on the screen ,where central bright fringe was formed before the introduction of the glass sheets,is now occupied by the `15th`bright fringe.Assuming that both the glass plates have same thickness and wavelength of light used in `4800Å` ,find the their thickness.
View SolutionPhase difference at the central point changes by `pi//3` when as thick film having a refractive index 1.5 and thickness `0.4mum` is placed in front of upper slit of a YDSE set up. If the wavelength (in nm) of the light used is 600 k, find k.
View SolutionA monchromatic beam of electrons accelerated by a potential difference V falls normally on the plate containing two narrow slits seperated by a distance d. The interference pattern is observed on a screen parallel to the plane of the slit and at a distance of D from slits. Fringe width is found to be `omega_(1)`. When electron beam is accelerated by the potential differene of 4V, the finge width becomes `omega_(2)`. Find the ratio `(omega_(1))/(omega_(2))`. (Given `dltltD`)
View SolutionThe outer surface of a transparent glass slab of refractive index `mu_(S)=1.5` is coated by a thin layer of transparent medium of refractive index `mu_(C)=1.6`. Orange light of wavelength 6400Å falls normally on the coating. The reflected light at the upper surface and at the lower surface of teh coat interfere destructively. If thickness of the coat is `5Kxx10^(-8)`m, calculate the minimum value of K.
View SolutionIn a Young's double slit experiment, slits are seperated by a distance d and screen is at distance D, `(D gt gt d)` from slit plane. If light source of wavelength `lambda(lambda ltlt d)` is used. The minimum distance from central point on the screen where intensity is one fourth of the maximum is `(D lambda)/(nd)`. Find the value of n.
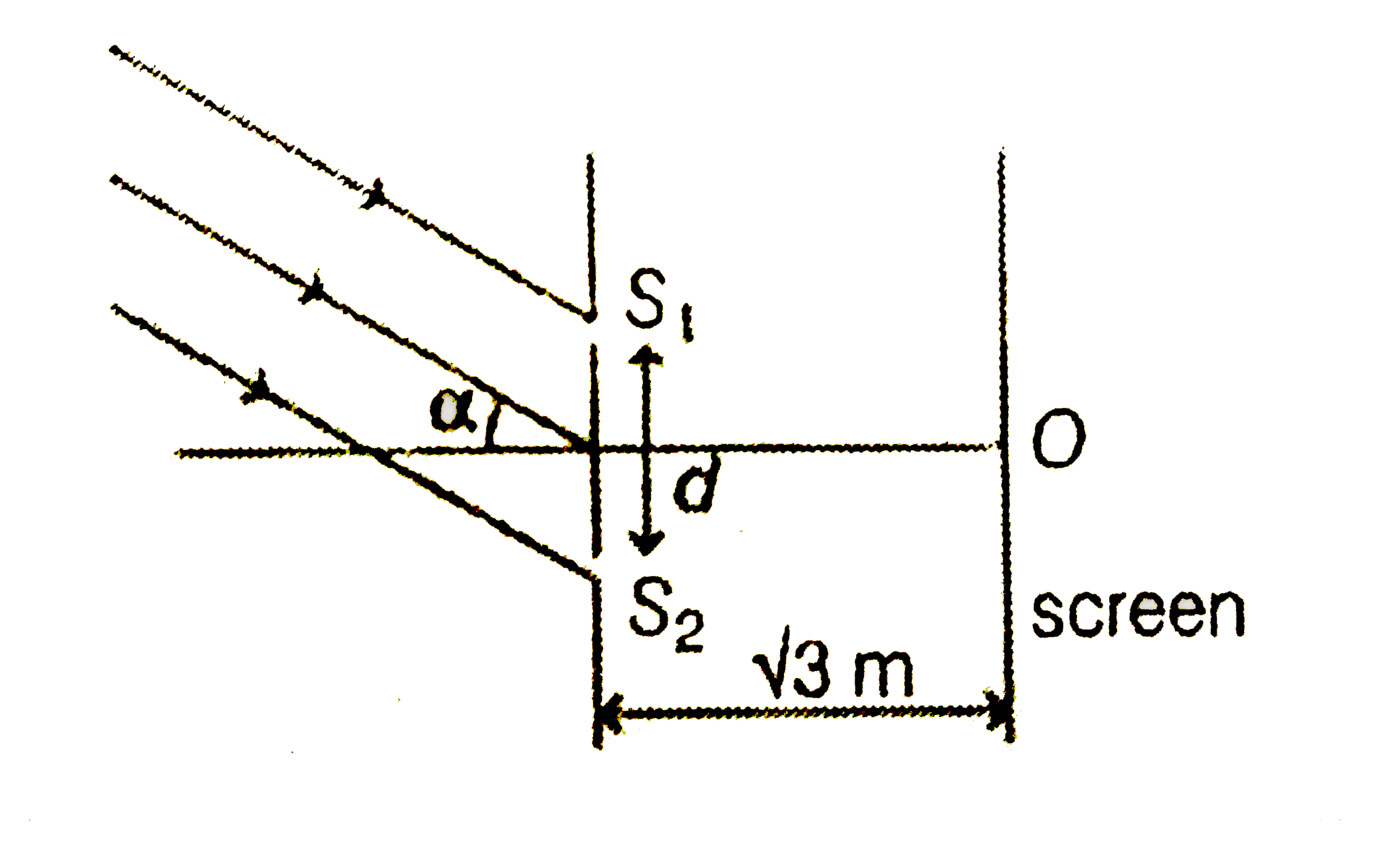
View SolutionA parrallel beam of light `(lambda=5000Å)` is incident at an angle `alpha=30^(@)` as shown in YDSE experiment. Intensity due to each slit at any point on screen in `I_(0)`. The distance between slits is 1mm. The intensity at central point O on the screen is `KI_(0)`. Find the value of K.
View SolutionIn a Young's double slit experiment, one of the slits is covered by a thin film of thickness t=0.04 mm, and refractive index `mu=1.2+(9xx10^(-14)m^(2))/(lambda^(2))`, where `lambda` is the wavelength in meter. A beam of light consisting of two wavelength `lambda_(1)=400nm and lambda_(2)=600 nm ` falls normally on the plane of the slits. Find the distance between two central maxima in milimeter. Distance of screen from slits is 400 times the the separation between the slits.
View Solution
For JEE Advanced E. Integer Type Questions questions and complete solutions for chapter WAVE OPTICS of DC PANDEY PHYSICS (HINGLISH) of Class 12
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 12 PHYSICS WAVE OPTICS
- Assertion reason
- Check point
- Example
- For JEE Advanced B. More than one option is correct
- For JEE Advanced C. Comprehension Type Questions. Passage (I)
- For JEE Advanced C. Comprehension Type Questions. Passage (II)
- For JEE Advanced C. Comprehension Type Questions. Passage (III)
- For JEE Advanced D. Matrix Matching type Questions.
- For JEE Advanced E. Integer Type Questions
- For JEE Advanced Only one option is correct
- For JEE main (Only one option is Correct )
- match column
- medical entrances
- taking it together