Complete Solutions to CHAPTER EXERCISES of chapter NUCLEI of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NUCLEI |
| DC PANDEY NEET | CHAPTER EXERCISES |
| Number Of Questions | 78 |
| Academic Year | 2023-24 |
Following process is known as `hv rarr e^(+) +e^(-)`
View SolutionThe operation of a nuclear reactor is said to be critical, if the multiplication factor (k) has a value
View SolutionWhich of the following is not used for the treatment of cancer
View SolutionIdentify the correct statement given below.
View SolutionWhen a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom.
View SolutionHeavy stable nuclei have more neutrons than protons. This is because of the fact that
View SolutionIn one average-life,
View SolutionWhich of the following is a wrong description of binding energy of a nucleus?
View SolutionAs compared to `^12C` atom, `^14C` atoms has
View SolutionWhen the number of nucleons in a nuclues increases the binding energy per nucleon
View SolutionThe binding energy per nucleon is maximum in the case of.
View SolutionWhich of the following process will result into fission reaction ?
View SolutionWhat fissionable material was used in the bomb dropped at Nagasaki (Japan) in the year 1945 ?
View SolutionThe principle of controlled chain reaction is used in.
View SolutionIn an atom bomb, the energy is released because of the.
View SolutionBoron rods are used in nuclear reactors because
View SolutionA nuclear reaction along with the masses of the particle taking part in it is as follows
`underset("amu")underset(1.002)A+underset("amu")underset(1.004)Btounderset("amu")underset(1.001)C+underset("amu")underset(1.003)D+QMeV`
The energy Q liberated in the reaction is
View SolutionThe curve of blinding energy per nucleon as a function of atomic mass number has a sharp peak for helium nucleus. This implies that helium.
View SolutionIn the given nuclear reaction `A, B, C, D, E` represents `._92 U^238 rarr^(alpha) ._BTh^A rarr^(beta) ._D Pa^C rarr^(E) ._92 U^234`.
View SolutionAn atom of mass number `15` and atomic number `7` captures an `alpha-`particle and then emits a proton. The mass number and atomic number of the resulting product will respectively be.
View SolutionThe binding energies of the nuclei A and B are `E_(alpha)and E_(alpha)` respectively. Three atoms of the element B fuse to give one atom of element A and an energy Q is released. Then, `E_(a),E_(b)` Q are relaetd as
View SolutionThe total number of `alphaandbeta` particles emitted in the nuclear reaction
`""_(92)^(238)Uto""_(82)^(214)Pb` is
View SolutionSuppose we consider a large number of continers each containing initially `10000` atoms of a radioactive material with a half life of `1` year. After `1` year.
View Solution`90%` of a radioactive sample is left undecayed after time `t` has elapesed. What percentage of the initial sample will decay in a total time `2 t` ?
View Solution`M_(x) and M_(y)` denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The Q - value for a `beta-` decay is `Q_(1)` and that for a `beta^(+)` decay is `Q_(2)`. If `m_(e)` denotes the mass of an electrons, then which of the following statements is correct?
View SolutionHalf life of a radio-active substance is `20` minutes. The time between `20 %` and `80 %` decay will be
View SolutionA freshly prepared radioactive source of half-life `2 h` emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
View SolutionThe decay constant of a radioactive sample is `'lambda'`. The half-life and mean life of the sample are respectively a)`1/lamda,("in"2)/lamda` b)`("in"2)/lamda,1/lamda` c)`"in"2,1/lamda` d)`lamda/("in"2),1/lamda`
View SolutionA radioactive substance disintegrates 1/64 of initial value in 60 s. The half-life of this substance is
View SolutionIn the reaction `._1^2 H + ._1^3 H rarr ._2^4 He + ._0^1 n`, if the binding energies of `._1^2 H, ._1^3 H` and `._2^4 He` are respectively `a,b` and `c` (in MeV), then the energy (in MeV) released in this reaction is.
View SolutionA radioactive sample has `N_0` active at `t = 0` . If the rate of disintegration at any time is `R` and the number of atoms is `N`, them the ratio `R//N` varies with time as.
View SolutionThe plot of the number (N) of decayed atoms versus activity (R) of a radioactive substance is
View SolutionThe graph between the instantaneous concentration (N) of a radioactive element and time (t) is.
View SolutionTwo redioactive materials `X_(1)andX_(2)` have decay constants `10lamdaandlamda`, respecitvely. If initially they have the same number of nuclei, then the ratio of the number of nuclei of `X_(1)` to that of `X_(2)` will be 1/e after a time
View SolutionTwo redioactive nuclei A and B have disintegration constants `lamda_(A)andlamda_(B)` and initially `N_(A)andN_(B)` number of nuclei of them are taken, then the time after which their undisintegrated nuclei are same is
View SolutionWhat is the binding energy per nucleon of `_(6)C^(12)`nucleus?
Given , mass of `C^(12)` `(m_(c))_(m)` = 12.000 u
Mass of proton `m_(p)` = 1.0078 u
Mass of neutron `m_(n)` = 1.0087 u
and 1 amu = 931.4 MeV
View SolutionA radioactive isotope `X` with a half-life of `1.37 xx 109` years decays to `Y` which is stable. A sample of rock from the moon was found to contain both the elements `X` and `Y` which were in the ratio of `1 : 7`. The age of the rock is.
View SolutionThe energy released by the fission of a single uranium nucleus is `200 MeV`. The number of fission of uranium nucleus per second required to produce `16 MW` of power is (Assume efficiency of the reactor is `50%`)
View SolutionA common example of `beta-"decay"` is
`""_(15)P^(32)to""_(16)P^(32)+x+y`
Then, x and y stand for
View SolutionA nucleus with Z =92 emits the following in a sequence:
`alpha,beta^(-),beta^(-),alpha,alpha,alpha,alpha,alpha,beta^(-),beta^(-),alpha,beta^(+),beta^(+),alpha`. The Z of the resulting nucleus is
View SolutionBinding energy per nucleons vs mass curve for nucleus is shown in the figure `W, X, Y` and `Z` are four nuclei indicated on the curve . The process that would release energy is
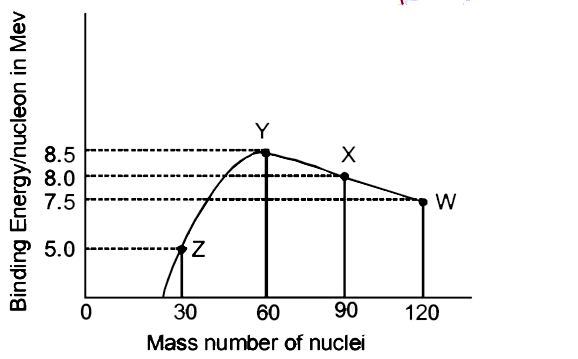
View SolutionTritium is an isotope of hydrogen whose nucleus triton contains 2 neutrons and 1 proton . Free neutrons decay into `p+bar(e) +bar(n).` If one of the neutrons in Triton decays , it would transform into `He^(3)` nucleus. This does not happen. This is because
View SolutionThe gravitational force between a H-atom and another particle of mass m will be given by Newton's law: `F=G (M.m)/(r^(2)`, where r is in km and
View SolutionIn a sample of radioactive material, what fraction of initial number of active nuclei will remain undistintegrated after half of a half0life of the sample?
View SolutionIn a radioactive sample, the fraction of initial number of redioactive nuclie, which remains undecayed after n mean lives is
View SolutionAt any instant, the ratio of the amounts of two radioactive substance is `2:1`. If their half-lives be, respectively, `12h` and `16h`, then after two days, what will be the ratio of the substances?
View SolutionA radioactive isotope X with half-life `1.5xx10^(9)` yr decays into a stable nucleus Y .A rock sample contains both elements X and Y in the ratio 1 : 15. They age of the rock is
View SolutionThe half-life of a sample of a radioactive substance is `1` hour. If `8 xx 10^10` atoms are present at `t = 0`, then the number of atoms decayed in the duration `t = 2` hour to `t = 4` hour will be
View SolutionHalf-life of a radioactive substance is `20` minutes. Difference between points of time when it is `33 %` disintegrated and `67 %` disintegrated is approximate.
View Solution`A` and `B` are two radioactive substances whose half lives are `1` and `2` years respectively. Initially `10 gm` of `A` and `1 gm` of `B` is taken. The time (approximate) after which they will have same quantity remaining is.
View SolutionThe decay constant of a radioactive element is defined as the reciprocal of the time interval after which the number of atoms of the radioactive element falls to neraly
View SolutionThey decay constant of radioactive element is `1.5xx10^(9)s^(-1)` Its mens-life (in second) will be
View SolutionA radioactive material has mean lives of 1620 yr and 520 yr for `alphaandbeta-"emission"`, respectively. The material decays by simultaneous `alphaandbeta-"emissions`. The time in which 1/4th of the material remains intact is
View SolutionA radioactive nucleus is being produced at a constant rate `alpha` per second. Its decay constant is `lamda`. If `N_0` are the number of nuclei at time `t = 0`, then maximum number of nuclei possible are.
View SolutionAfter three 'average life times' of a radioactive sample, the amount of substance remains x% of the original amount. Then, approximate value of x is
View SolutionAn archaeologist analyses the wood in a phehistoric structure and finds that `C^14` (Half-life `= 5700` years) to `C^12` only one-fourth of that found in the cells buried plants. The age of the wood is about
View SolutionA radioactive element A of decay constant `lamda_(A)` decays into another radioactive element B of decay constant `lamda_(B)`. Initially the number of active nuclei of A was `N_(0)` and B was absent in the sample. The maximum number of active nuclei of B is found at t=2. In `2//lamda_(A)`. The maximum number of active nuclei of B is
View SolutionTwo identical samples (same material and same amout) `P and Q` of a radioactive substance having mean life `T` are observed to have activities `A_P` and `A_Q` respectively at the time of observation. If `P` is older than `Q`, then the difference in their age is
View SolutionAn energy of `24.6 eV` is required to remove one of that electrons from a neutal helium atom. The enegy (in `eV`)required to remove both the electrons from a netural helium atom is
View SolutionThe activity of a sample of radioactive material is `R_(1)` at time `t_(1)andR_(2)"at time"t_(2)(t_(2)gtt_(1))`. Its mean life is T. Then,
View SolutionA heavy nucleus at rest breaks into two fragments which fly off with velocities in the ratio `8 : 1`. The ratio of radii of the fragments is.
View SolutionFor a substance the average life for `alpha-`emission is `1620` years and for `beta-`emission is `405` years. After how much time the `1//4` of the material remains after `alpha` and `beta` emission ?
View SolutionTwo radioactive nuclei `P` and `Q`, in a given sample decay into a stable nucleus `R`. At time `t = 0`, number of `P` species are `4 N_0` and that of `Q` are `N_0`. Half-life of `P` (for conversation to `R`) is `1mm` whereas that of `Q` is `2 min`. Initially there are no nuclei of `R` present in the sample. When number of nuclei of `P` and `Q` are equal, the number of nuclei of `R` present in the sample would be :
View SolutionThe half-life a radioacitve substance is `40` yeard. How long will it take to reduce to one fourth of its original amount and what is the value of decay constant ?
View SolutionStarting with a sample of pure `.^66 Cu, 7//8` of it decays into `Zn` in `15 min`. The corresponding half-life is.
View SolutionA stationary radioactive nucleus of mass 210 units disintegrates into an alpha particle of mass 4 units and residual nucleus of mass 206 units. If the kinetic energy of the alpha particle is E, then the kinetic energy of the residual nucleus is
View SolutionA bone containing `200 g` carbon-14 has `beta`-decay rate of `375` decay/min. Calculate the time that has elapsed since the death of the living one. Given the rate of decay for the living organism is equal to `15` decay per min per gram of carbon and half-life of carbon-14 is `5730 years`.
View SolutionAssuming that about `200 MeV` of energy is released per fission of `._(92)U^(235)` nuceli, the mass of `U^(235)` consumed per day in a fission ractor of power `1` megawatt will be approximately .
View SolutionThe activity of a radioactive sample is measures as `N_0` counts per minute at `t = 0` and `N_0//e` counts per minute at `t = 5 min`. The time (in minute) at which the activity reduces to half its value is.
View SolutionIn the nuclear fusion reaction
`_(1)^(2)H + _(1)^(3)H rarr _(2)^(4)He + n `
given that the repulsive potential energy between the two nuclei is `- 7.7 xx 10^(-14) J` , the temperature at which the gases must be heated the reaction is nearly
[Boltzmann's constant `k = 1.38 xx 10^(-23) J//K]`
View SolutionThe half life of radioactive Radon is `3.8 days` . The time at the end of which `(1)/(20) th` of the radon sample will remain undecayed is `(given log e = 0.4343 ) `
View SolutionThe half-life of radioactive Polonium `(Po)` is `138.6` days. For ten lakh Polonium atoms, the number of disintegrations in `24` hours is.
View SolutionIf half-life of a substance is `3.8` days and its quantity is `10.38 gm`. Then substance quantity remaining left after `19` days will be
View SolutionTwo radioactive substance `A` and `B` have decay constants `5 lambda` and `lambda` respectively. At `t=0` they have the same number of nuclei. The ratio of number of nuclei of nuclei of `A` to those of `B` will be `(1/e)^(2)` after a time interval
View SolutionA star initially has `10^(40) ` deuterons. It produces energy via the process `_(1)H^(2) + _(1)H^(2) + rarr _(1) H^(3) + p. `and `_(1)H^(2) + _(1)H^(3) + rarr _(2) He^(4) + n` .If the average power radiated by the state is `10^(16) W` , the deuteron supply of the star is exhausted in a time of the order of .
The masses of the nuclei are as follows:
`M(H^(2)) = 2.014 amu,`
`M(p) = 1.007 amu, M(n) = 1.008 amu, M(He^(4)) = 4.001 amu`.
View SolutionThe sun radiates energy in all directions. The average radiations received on the earth surface from the sun is `1.4 "kilowatt"//m^2`. The average earth-sun distance is `1.5 xx 10^11` meters. The mass lost by the sun per day is.
View SolutionIf `10%` of a radioactive material decays in `5` days, then the amount of original material left after `20` days is approximately.
View SolutionA small quantity of solution containing `Na^24` radio nuclide `(half-life=15 h)` of activity `1.0 microcurie` is injected into the blood of a person. A sample of the blood of volume `1cm^3` taken after `5h` shows an activity of `296` disintegrations per minute. Determine the total volume of the blood in the body of the person. Assume that the radioactive solution mixes uniformly in the blood of person.
(1 curie `=3.7 xx 10^10` disintegrations per second)
View Solution
CHAPTER EXERCISES questions and complete solutions for chapter NUCLEI of DC PANDEY PHYSICS (HINGLISH) of Class 12