Complete Solutions to physics of chapter MOTION IN A PLANE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| DISHA | physics |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
A man whirls a stone round his head on the end of a string 4.0 metre long. Can the string be in a horizontal, plane? If the stone has a mass of 0.4 kg and the string will break, if the tension in it exceeds 8 N. The smallest angle the string can make with the horizontal and the speed of the stone will respectively be (Take `g=10 m/s^(2)`)?
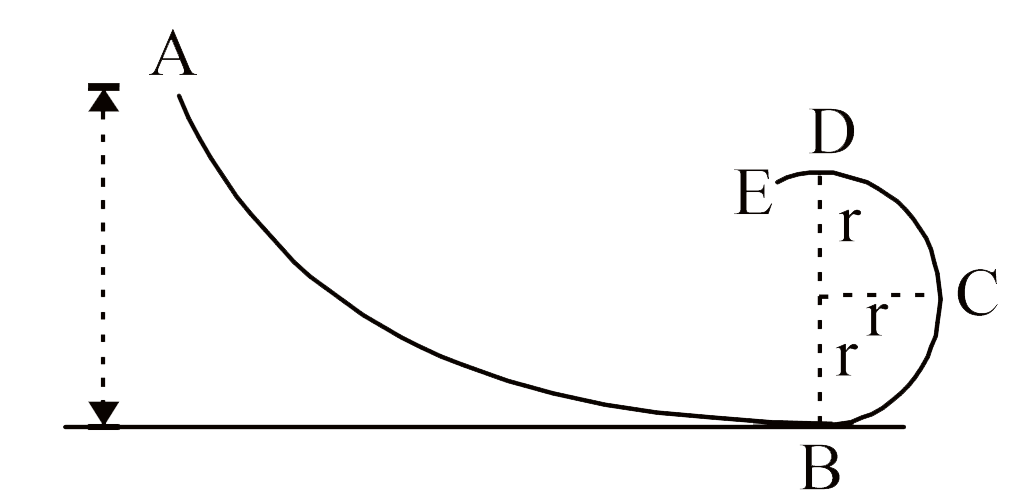
View SolutionIn figure ABCDE is a channel in the vertical plane, part BCDE being circular with radius r. A ball is released from A and slides without friction and without rolling. It will complete the loop path when
View SolutionAn aircraft loops the loop of radius R = 500 m with a constant velocity v = 360km//h. The weight of the flyer of mass m = 70 kg in the lower, upper and middle points of the loop will respectively be-
View SolutionA particle of mass 3 kg is moving under the action of a central force whose potential energy is given by U(r) = 10r3 joule. For what energy and angular momentum will the orbit be a circle of radius 10 m ?
View SolutionA string of length 1 m is fixed at one end and carries a mass of 100 gm at the other end. The string makes `2//pi`revolutions per second about a vertical axis through the fixed end. The angle of inclination of the string with the vertical, and the linear velocity of the mass will respec- tively be - (in M.K.S. system)
View SolutionA particle of mass `m` is moving in a circular path of constant radius `r`, such that its centripetal force `F_r` varies with time `t` as `F_r=K^2rt^2`, where k is a constant. What is the power delivered to the particle by the forces acting on it?
View SolutionA car is moving in a circular path of radius 100 m with velocity of 200 m/sec such that in each sec its velocity increases by 100 m/s, the net acceleration of car will be - (in m/sec)
View SolutionA 4 kg balls is swing in a vertical circle at the end of a cord 1 m long. The maximum speed at which it can swing if the cord can sustain maximum tension of 163.6 N will be
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionA swimmer can swim in still water at a rate 4.0 km/h. If he swims in a river flowing at 3.0 km/h and keeps his direction (with respect to water) perpendicular to the current, find his velocity with respect to the ground.
View SolutionThe roadway bridge over a canal is the form of an arc of a circle of radius 20 m. What is the minimum speed with which a car can cross the bridge without leaving contact with the ground at the highest point (g = 9.8 m/s2
View SolutionA cane filled with water is revolved in a vertical circle of radius 0.5 m and the water does not fall down. The maximum period of revolution must be -
View SolutionA particle of mass m slides down from the vertex of semi- hemisphere, without any initial velocity. At what height from horizontal will the particle leave the sphere-
View SolutionA body of mass m tied at the end of a string of length l is projected with velocity `sqrt(4lg),` at what height will it leave the circular path
View SolutionA string of length `L` is fixed at one end and carries a mass `M` at the other end. The string makes `2//pi` revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.

View SolutionA train has to negotiate a curve of radius 400 m. By how much should the outer rail be raised with respect to inner rail for a speed of 48 km/hr. The distance between the rails is 1 m.
View SolutionA ship is streaming due West at ` 12 m^(-1)`. A boy runs across the beach at ` 5 ms^(-1)` in a direction at right angles to the direction of motion of the ship towards South, Calculate the velocity of the boy relative to sea.
View SolutionA man is walking on a level road at a speed of 3.0 km/h. Rain drops fall vertically with a speed of 4.0 km/h. Find the velocity of the raindrops with respect to the man.
View SolutionA stone of mass 1kg tied to a light inextensible sstring of length `L=10m` is whirling in a circular path of radius `L` in vertical plane. If the ratio of the maximum tension in the string to the minimmum tension in the string is 4 and if `g` is taken to be `10ms^(-2)` , the speed of the stone at the highest point of the circle is.
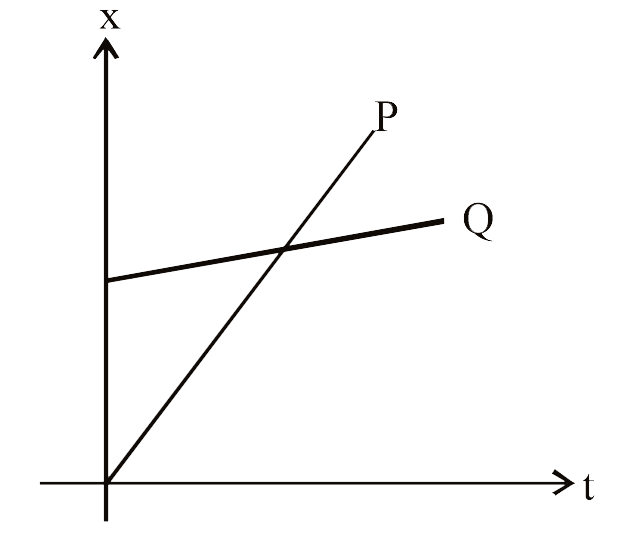
View SolutionTwo bodies P and Q are moving along positive x-axis their position-time graph is shown below. If `vecV_(PQ)` is velocity of
View SolutionConsider two children riding on the merry-go-round Child 1 sits near the edge, Child 2 sits closer to the centre. Let`V_(1)"and"V_(2) denote the linear speed of child 1 and child 2, respectively. Which of the following is/are wrong ?
View SolutionThere of the fundamental constant of physics are the universal gravitational constant, `G=6.7xx10^(-11) m^(3) kg^(-) s^(-2)`, the speed of light `c=3.0xx10^(8) m//s` and Planck's constant, `h=6.6xx10^(-34) Js^(-1)`. two particles A and V are projected in the vertical plane with same initial velocity `u_(0)` fro part (0,0) and (l,-h) towards each other as shwon in figure
The path of particle A with respect to particle B will be –

View SolutionThere of the fundamental constant of physics are the universal gravitational constant, `G=6.7xx10^(-11) m^(3) kg^(-) s^(-2)`, the speed of light `c=3.0xx10^(8) m//s` and Planck's constant, `h=6.6xx10^(-34) Js^(-1)`. two particles A and V are projected in the vertical plane with same initial velocity `u_(0)` fro part (0,0) and (l,-h) towards each other as shwon in figure
Minimum distance between particle A and B during motion

View SolutionThere of the fundamental constant of physics are the universal gravitational constant, `G=6.7xx10^(-11) m^(3) kg^(-) s^(-2)`, the speed of light `c=3.0xx10^(8) m//s` and Planck's constant, `h=6.6xx10^(-34) Js^(-1)`. two particles A and V are projected in the vertical plane with same initial velocity `u_(0)` fro part (0,0) and (l,-h) towards each other as shwon in figure
The time when separation between A and B is minimum is

View SolutionStatement-1 : The relative velocity between any two bodies moving in opposite direction is equal to sum of the velocities of two bodies. Statement-2 : Sometimes relative velocity between two bodies is equal to difference in velocities of the two.
View SolutionStatement-1: A river is flowing from east to west at a speed of 5m/min. A man on south bank of river, capable of swimming 10 m/min in still water, wants to swim across the river in shortest time. He should swim due north. Statement-2 : For the shortest time the man needs to swim perpendicular to the bank.
View SolutionStatement-1 : Rain is falling vertically downwards with velocity 6 km/h. A man walks with a velocity of 8 km/h. Relative velocity of rain w.r.t. the man is 10 km/h. Statement-2 : Relative velocity is the ratio of two velocities
View SolutionThe path followed by a body projected along y axis is given by `y=sqrt(3)x-(1//2)x^(2)` . If `g=10ms^(2)`, then the initial velocity of projectile will be – (x and y are in m)
View SolutionWhen the angle of elevation of a gun are `60^(@)` and `30^(@)` respectively, the height it shoots are `h_(1)` and `h_(2)` respectively, `h_(1)//h_(2)` equal to –
View SolutionIf `t_(1)` be the time taken by a body to clear the top of a building and `t_(2)` be the time spent in air, then `t_(2):t_(1)` will be -
View SolutionThe co-ordinates of a moving particle at any time t are given by `x=ct^(2) and y=bt^(2)`The speed of the particle is
View SolutionThe height `y` and the distance `x` along the horizontal plane of a projectile on a certain planet (with no surrounding atmosphere) are given by `y = (8t - 5t^2) m` and `x = 6tm`, where `t` is in seconds. The velocity with which the projectile is projected at `t = 0` is.
View SolutionA body is thrown at an angle `30^(@)` to the horizontal with the velocity of `30m//` After 1 sec. its velocity will be ("in"m//s) `(g=10 m//s^(2))`
View SolutionA particle is moving in a plane with a velocity given by, `vecu=u_(0)hati+(omegacosomegat) hatj,` are unit vectors along x and y-axes respectively. If the particle is at the origin an `t=0,` then its distance from the origin at time`t=3pi//2omega` will be
View SolutionA ball thrown by one player reaches the other in `2 s`. The maximum height attained by the ball above the point of projection will be about.
View SolutionA ball is projeced from O with an initial velocity 700 cm/ s in a direction `37^(@)` above the horizontal. A ball B, 500 cm away from O on the line of the initial velocity of A, is released from rest at the instant A is projected. The height through which B falls, before it is hit by A and the direction of the velocity A at the time of impact will respectively be [Given `g=10m//s^(2), sin 37^(@)=0.6 and cos 37^(@)=0.8`]
View Solution5A ball is thrown horizontally from a height of 20 m. It hits the ground with a velocity three times its initial velocity. The initial velocity of ball is
View SolutionA projectile thrown from a height of 10 m with velocity of `sqrt(2)m//s` the projectile will fall, from the foot of projection, at distance- `(g=10m//s^(2))`
View SolutionSavita throws a ball horizontally with a velocity of 8 m/s from the top of her building. The ball strikes to her brother Sudhir playing at 12 m away from the building. What is the height of the building ?
View SolutionA body is projected downwards at an angle of ` 30^@` to the horizontal with a velocity of `9.8 m//s` from the top of a a tower ` 29 .4m` high. How long will it take before striking the ground ?
View SolutionA ball is thrown from the top of a tower with an initial velocity of 10 m//s at an angle of `30^(@)`above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower `(g=10m//s^(2))` will be
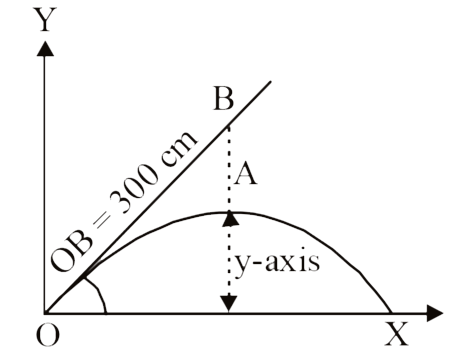
View SolutionA ball 'A' is projected from origin with an initial velocity `v_(0)` = 700 cm/sec in a direction `37^(@)` above the horizontal as shown in fig .Another ball 'B' 300 cm from origin on a line `37^(@)` above the horizontal is released from rest at the instant A starts. How far will B have fallen when it is hit by A ?
View SolutionA ball projected with speed 'u' at an angle of projection `15^(@)` has range R. The other angle of projection at which the range will not be same with same initial speed 'u' is
View SolutionA projectille can have the same range` R` for two angles of projection. If ` t_(1)` and `t_(2)` be the time of flight in the two cases, then find the relation between ` t_(1), t_(2)` and `R` .
View SolutionVelocity at a general point P(x, y) for a horizontal projectile motion is given by
`v=sqrt((v_("x")^(2)+v_("y")"^(2))),tan alpha=(v_(y))/(v_(x))`
`alpha`is angle made by v with horizontal in clockwise direction Trajectory equation for a horizontal projectile motion is given by `x=v_(x)t=ut`
y=-`(1//2)"gt"^(2)`
eliminating t, we get `y=-(1//2)(gx^(2))/(u^(2)`
A ball rolls off top of a stair way with a horizontal velocity u m//s. If the steps are h m high and b meters wide, the ball will just hit the edge of nth step if `n^(th) equals to
View Solutionelocity at a general point P(x, y) for a horizontal projectile motion is given by
`v=sqrt((v_("x")^(2)+v_("y")"^(2))),tan alpha=(v_(y))/(v_(x))`
`alpha`is angle made by v with horizontal in clockwise direction Trajectory equation for a horizontal projectile motion is given by `x=v_(x)t=ut`
y=-`(1//2)"gt"^(2)`
eliminating t, we get `y=-(1//2)(gx^(2))/(u^(2)`
5An aeroplane is in a level flying at an speed of 144 km//hr at an altitude of 1000 m. How far horizontally from a given target should a bomb be released from it to hit the target ?
View SolutionVelocity at a general point P(x, y) for a horizontal projectile motion is given by
`v=sqrt((v_("x")^(2)+v_("y")"^(2))),tan alpha=(v_(y))/(v_(x))`
`alpha`is angle made by v with horizontal in clockwise direction Trajectory equation for a horizontal projectile motion is given by `x=v_(x)t=ut`
y=-`(1//2)"gt"^(2)`
eliminating t, we get `y=-(1//2)(gx^(2))/(u^(2)`
An aeroplane is flying horizontally with a velocity of 720 km/h at an altitude of 490 m. When it is just vertically above the target a bomb is dropped from it. How far horizontally it missed the target?
View SolutionStatement -1 : Two projectiles are launched from the top of a cliff with same initial speed with different angles of projection. They reach the ground with the same speed. Statement -2 : The work done by gravity is same in both the case
View SolutionStatement-1 : A man projects a stone with speed u at some angle. He again projects a stone with same speed such that time of flight now is different. The horizontal ranges in both the cases may be same. (Neglect air friction) Statement-2 : The horizontal range is same for two projectiles projected with same speed if one is projected at an angle q with the horizontal and other is projected at an angle` (90^(@) theta) `with the horizontal. (Neglect air friction)
View SolutionA particle completes 1.5 revolutions in a circular path of radius 2 cm. The angular displacement of the particle will be – (in radian)
View SolutionA particle revolving in a circular path completes first one third of circumference in 2 sec, while next one third in 1 sec. The average angular velocity of particle will be – ("in "rad//sec)
View SolutionThe ratio of angular speeds of minute hand and hour hand of a watch is
View SolutionThe angular displacement of a particle is given by `theta=omega_(0)t+(1)/(2) alpha^(2), "and" alpha` are constatnt velocity at time, `t=2` sec will be ("in" rad//sec)-
View SolutionFind the magnitude of the linear acceleration of a particle moving in a circle of radius 10 cm with uniform speed completing the circle in 4s.
View SolutionA cane filled with water is revolved in a vertical circle of radius 4 m and water just does not fall down. The time period of revolution will be –
View SolutionThe length of second's hand in watch is `1 cm`. The change in Velocity of its tip in 15 seconds is
View SolutionAn electron is moving in a circular orbit of radius `5.3xx10^(-11)` metre around the atomic nucleus at a rate of `6.6xx10^(15)` revolutions per second. The centripetal force acting on the electron will be - (The mass of the electron is `9.1xx10^(-31)`kg)
View SolutionAn air craft executes a horizontal loop of radius ` 1 km` with steady speed of ` 900 km h^(-1)`. Compare its centripetal acceleration with the acceleration due to gravity.
View SolutionA car driver is negotiating a curve of radius 100 m with a speed of `18 km//hr.` The angle through which he has to lean from the vertical will be -
View SolutionStatement - 1 : If net force `vecF` acting on a system is changing in direction only, the linear momentum `(vec p)`of system changes in direction. Statement - 2 : In case of uniform circular motion, magnitude of linear momentum is constant but direction
View Solution
physics questions and complete solutions for chapter MOTION IN A PLANE of DISHA PHYSICS (HINGLISH) of Class 12