Complete Solutions to physics of chapter ROTATIONAL MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| DISHA | physics |
| Number Of Questions | 72 |
| Academic Year | 2023-24 |
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity omega. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
View SolutionThe angular momentum of a system of particles is conserved
View SolutionTwo rigid bodies A and B rotate with rotational kinetic energies `E_(A)` and `E_(B)` respectively. The moments of inertia of A and B about the axis of rotation are `I_(A)` and `I_(B)` respectively. If `I_(A) = I_(B)//4` and E_(A)= 100 E_(B), the ratio of angular momentum (L_(A)) of A to the angular momentum (L_(B)) of B is
View SolutionA uniform heavy disc is rotating at constant angular velocity `omega` about a vertical axis through its centre and perpendicular to the plane of the disc. Let L be its angular momentum. A lump of plasticine is dropped vertically on the disc and sticks to it. Which of the following will be constant?
View SolutionTwo discs of moment of inertia `I_(1)` and `I_(2)` and angular speeds `omega_(1)` and `omega_(2)` are rotating along the collinear axes passing through their center of mass and perpendicular to their plane. If the two are made to rotate combindly along the same axis the rotational `K.E.` of system will be
View SolutionA particle performing uniform circular motion gas angular momentum `L`. If its angular frequency is double and its kinetic energy halved, then the new angular momentum is :
View SolutionA round disc of moment of inertia `I_2` about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia `I_1` rotating with an angular velocity `omega` about the same axis. The final angular velocity of the combination of discs is.
View SolutionCalculate the angular momentum of a body whose rotational energy is 10 joule. If the angular momentum vector coincides with the axis of rotation and its moment of inertia about this axis is `8xx10^(-7)` kg m^(2)
View Solutionif the earth is treated as a sphere of radius Radn mass M, Its angular momentum about the axis of its rotation with period T, is
View SolutionIf the earth is a point mass of `6xx10^(24)` kg revolving around the sun at a distance of `1.5xx10^(8)` km and in time `T = 3.14 xx10^(7)s`. then the angular momentum of the earth around the sun is
View SolutionAn automobile engine develops `100` kilo`-`watt, when rotating at a speed of `1800 rev//min`. Find the torque developed by it.
View SolutionA constant torque acting on a uniform circular wheel changes its angular momentum from `A_(0)` to `4 A_(0)` in `4` seconds. Find the magnitude of this torque.
View SolutionA wheel having moment of inertia `2 kg m^(2)` about its vertical axis, rotates at the rate of `60 rpm` about this axis. The torque which can stop the wheel's rotation in one minute would be
View SolutionFind the torque of a force `vecF= -3hati+hatj+5hatk ` acting at the point `vecr=7hati+3hatj+hatk`
View SolutionA constant torque of `1000 N-m` turns a wheel of moment of inertia `200 kg-m^2` about an axis through its centre. Its angular velocity after `3` seconds is.
View SolutionA torque of `20 N-m` is applied on a wheel initially at rest. Calculate the angular momentum of the wheel after `3` sec.
View SolutionA horizontal force F is applied such that the block remains stationary, then which of the following statement is false
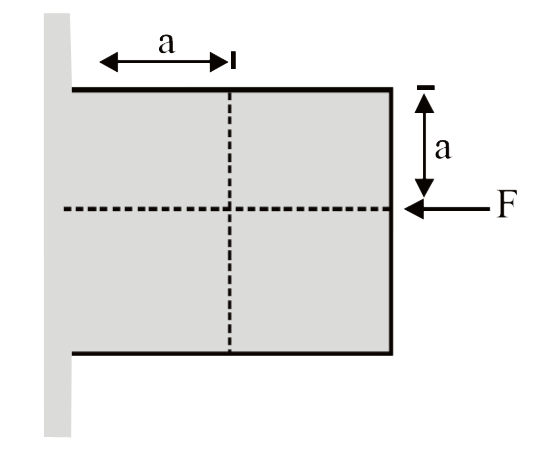
View SolutionIn a bicycle the radius of rear wheel is twice the radius of front wheel. If `v_F` and `v_r` are the speeds of top most points of front and rear wheels respectively, then :
View SolutionThe wheel of a car is rotating at the rate of 1200 revolutions per minute. On pressing the accelerator for 10 seconds, it starts rotating at 4500 revolutions per minute. The angular acceleration of the wheel is
View SolutionA wheel rotates with a constasnt acceleration of `2.0rad/s^2`. If the wheel starts from rest, how many evolutions wil it make in the first 10 senconds?
View SolutionA child is standing with folded hands at the center of a platform rotating about its central axis. The kinetic energy of the system is `K`. The child now stretches his arms so that the moment of inertia of the system doubles. The kinetic energy of the system now is
View SolutionTwo uniforms discs of equal mass but unequal radii are mounted on fixed horizontal axiles. Light strings are wrapped on each of the discs. The strings are pulled by constant equal forces F for same amount of time as shown in the figure
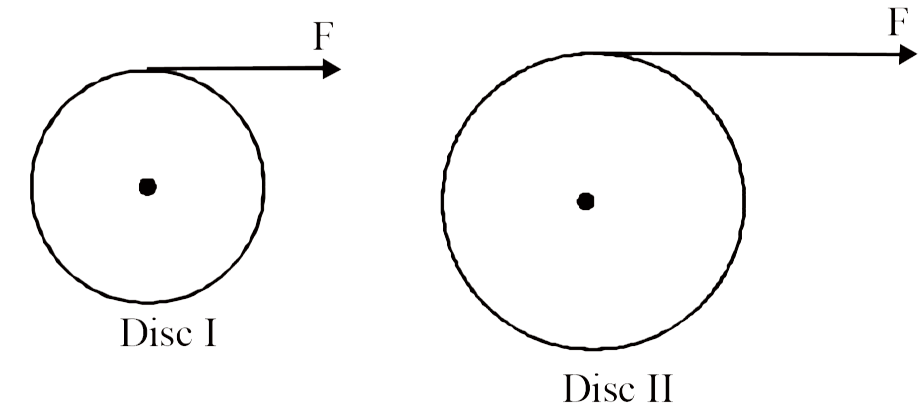
Angular momenta of discs are L1 and L2 and their kinetic energies are K1 and K2. Which of the following statements true –
`L_(1) = L_(2)`
`L_(1)ltL_(2)`
`K_(1)gtK_(2)`
`K_(1)=K_(2)`
View SolutionConsider a cylinder of mass `M=1 kg` and radius `R=1 m`lying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.
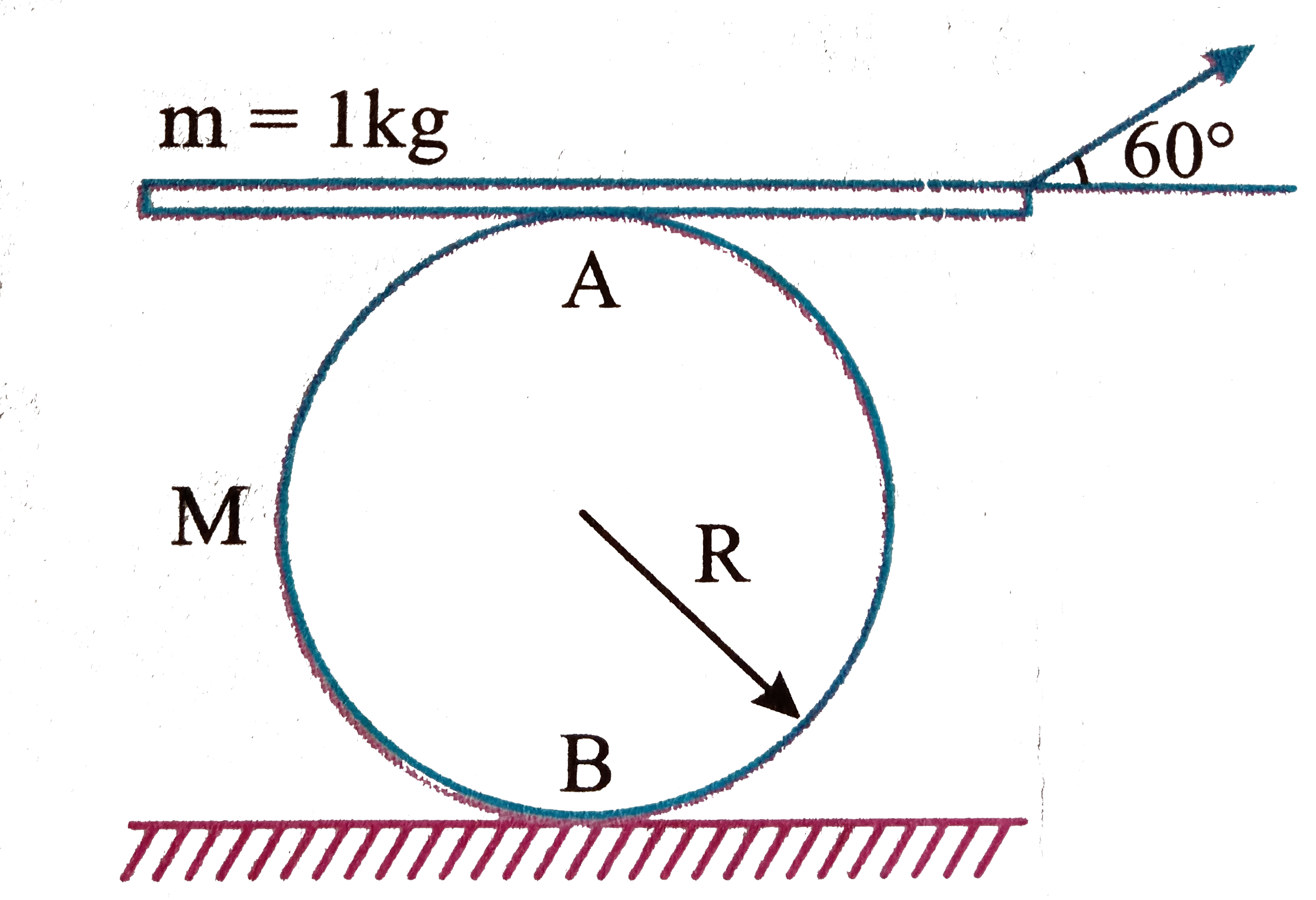
A force `F=55N` is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The acceleration of cylinder is
View SolutionConsider a cylinder of mass `M=1 kg` and radius `R=1 m`lying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.

A force `F=55N` is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The value of frictional force at `A` is
View SolutionConsider a cylinder of mass `M=1 kg` and radius `R=1 m`lying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.

A force `F=55N` is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The value of frictional force at `B` is
View SolutionStatement -1 : Torque is equal to rate of change of angular momentum .
Statement -2: Angular momentum depends on moment of inertia and angular velocity.
View SolutionStatement -1: Torque due to force is maximum when angle between `vec r and vecF is 90^(@)`.
Statement -2: The unit of torque is newton- meter.
View SolutionStatement -1: It is harder to open and shut the door if we apply force near the hinge
Statement -2: Torque is maximum at hinge of the door.
View SolutionFive particles of mass 2 kg are attached to the rim of a circular disc of radius 0.1 m & negligible mass. Moment of inertia of the system about an axis passing through the centre of the disc & perpendicular to its plane is
View SolutionTwo discs of the same material and thickness have radii 0.2 m and 0.6 m. Their moments of inertia about their axes will be in the ratio of
View SolutionA cylinder of 500 g and radius 10 cm has moment of inertia (about its natural axis)
View SolutionA constant torque of `31.4 N-m` id exterted on a pivoted wheel. If the angular acceleration of the wheel is `4 pi rad//s^2`, then the moment of inertia will be.
View SolutionFrom a uniform wire, two circular loops are made (`i`) `P` of radius `r` and (`ii`) `Q` of radius `nr`. If the moment of inertia of `Q` about an axis passing through its center and perpendicular to tis plane is `8` times that of `P` about a similar axis, the value of `n` is (diameter of the wire is very much smaller than `r` or `nr`)
View SolutionThe moment of inertia of a sphere of mass M and radius R about an axis passing through its centre is `(2)/(5) MR^(2)` . The radius of gyration of the sphere about a parallel axis to the above and tangent to the sphere is
View SolutionFour particles each of mass `m` are placed at the corners of a square of side length `l`. The radius of gyration of the system about an axis perpendicular to the plane of square and passing through its centre is
View SolutionThe radius of gyration of a disc of mass 50 g and radius 2.5 cm, about an axis passing through its centre of gravity and perpendicular to the plane is
View SolutionMoment of inertia of a ring of mass m = 3 gm and radius r = 1 cm about an axis passing through its edge and parallel to its natural axis is
View SolutionA disc is of mass M and radius r. The moment of inertia of it about an axis tangential to its edge and in plane of the disc or parallel to its diameter is
View SolutionTwo spheres each of mass `M` and radius `R//2` are connected at their centres with a mass less rod of length `2 R`. What will be the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod ?
View SolutionThree point masses `m_(1), m_(2)` and `m_(3)` are located at the vertices of an equilateral triangle of side `alpha`. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through `m_(1)?`
View SolutionThree rods each of length L and mass M are placed along X, Y and Z axis in such a way that one end of each of the rod is at the origin. The moment of inertia of this system about Z axis is
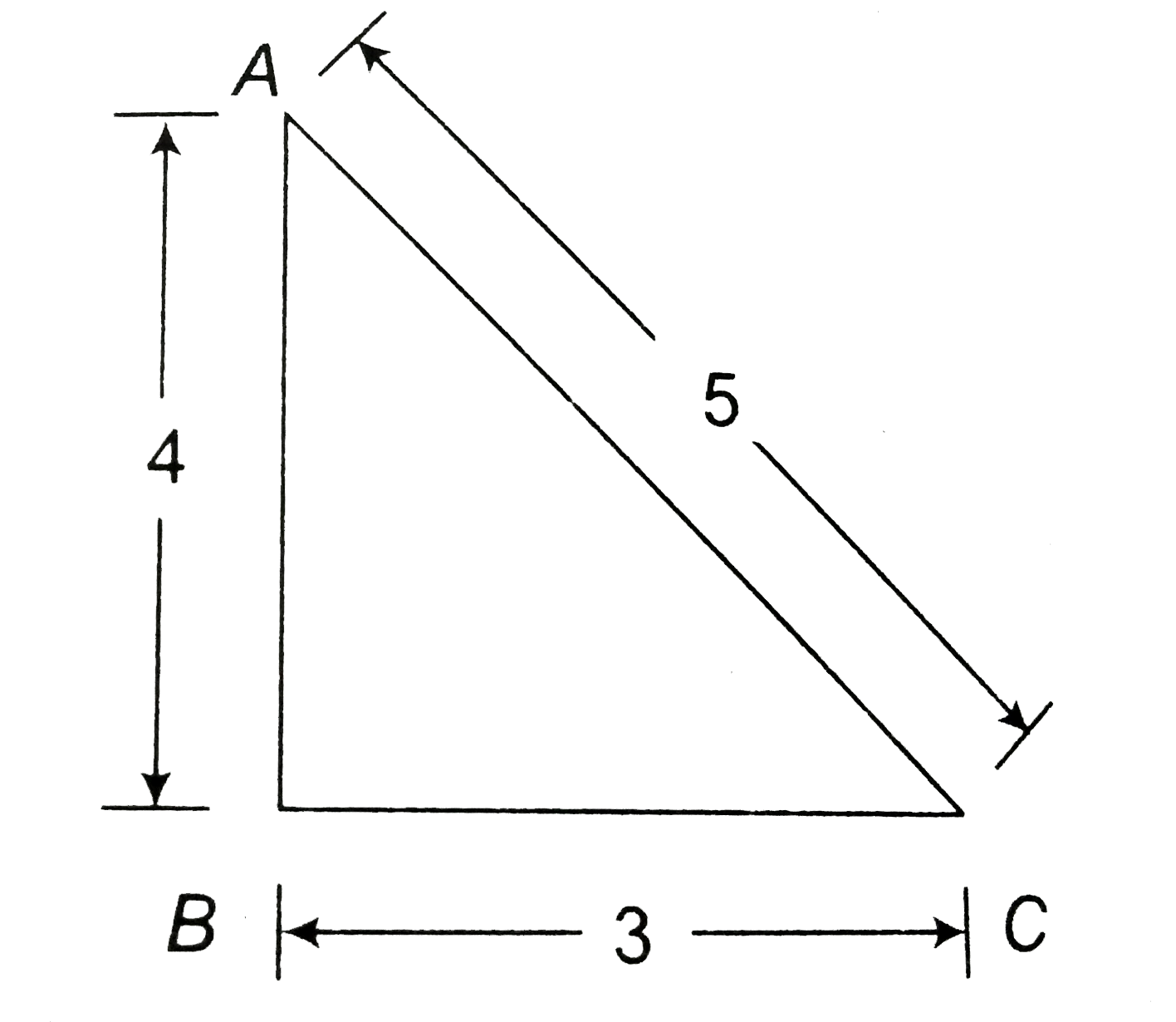
View Solution`ABC` is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. `I_(AB)`, `I_(BC)` and `I_(CA)` are the moments of inertia of the plate about `AB`, `BC` and `CA` repectively. Which one of the following relations is correct?
View SolutionA 1m long rod has a mass of 0.12 kg. The moment of inertia about an axis passin through the centre and perpendicular to the length of rod will be
View SolutionTwo rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring `= m`, radius `= r`)
View SolutionOne quarter sector is cut from a uniform circular disc of radius `R`. This sector has mass `M`. It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. It moment of inertia about the axis of rotation is.
 .
.
View SolutionA thin wire of length `L` and uniform linear mass density `rho` is bent into a circular loop with centre at `O` as shown. The moment of inertia of the loop about the axis `XX'` is :
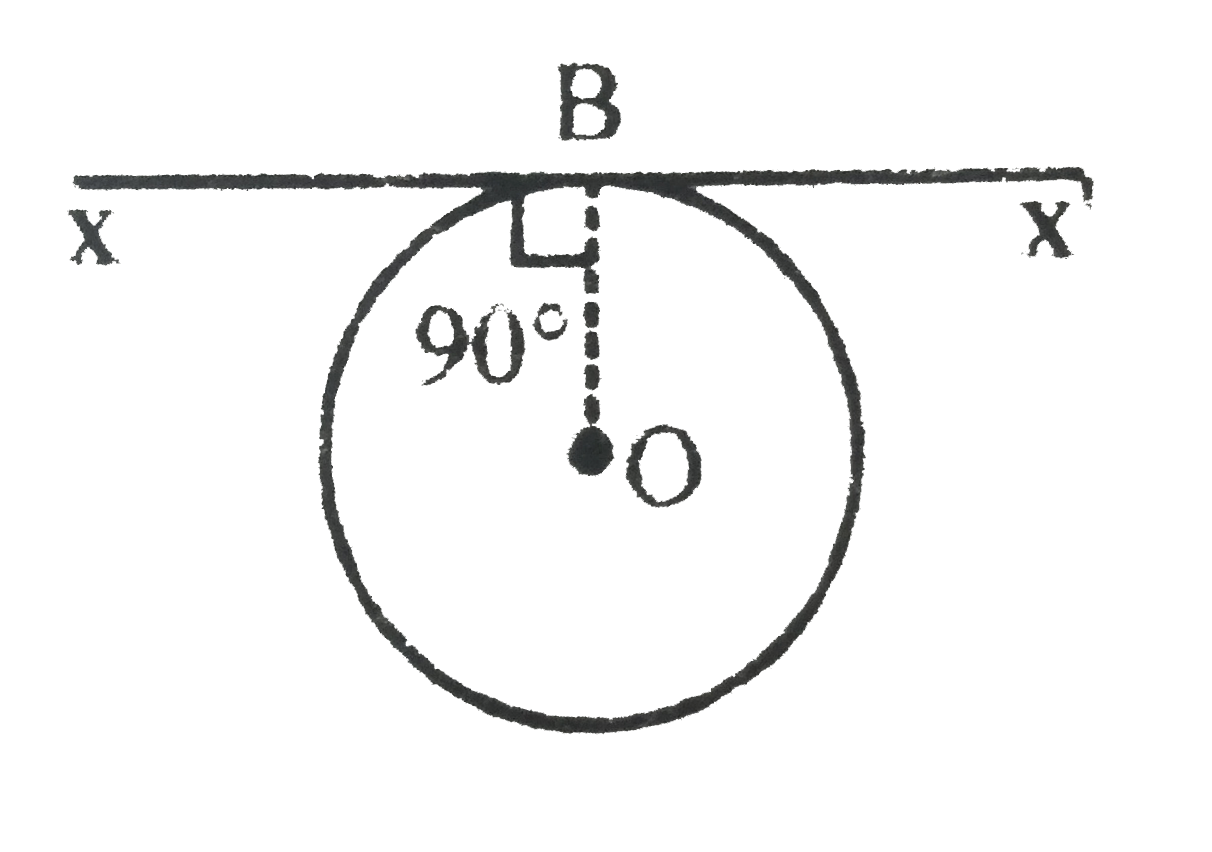 .
.
View SolutionTwo discs of same thickness but of different radii are made of two different materials such that their masses are same. The densities of the materials are in the ratio of `1 : 3.` The moments of inertia of these discs about the respective axes passing through their centres and perpendicular to their planes will be in the ratio of
View SolutionA circular disc of radius `R` and thickness `R//6` has moment of inertia `I` about an axis passing through its centre and perpendicular to its plane. It is melted and recast into a solid sphere. The `M.I` of the sphere about its diameter as axis of rotation is
View SolutionThree rings, each of mass `m` and radius `r`, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

View SolutionThe density of a rod AB increases linearly from A to B its midpoint is O and its centre of mass is at C. four axes pass through A, B, O and C, all perpendicular to the length of the rod. The moment of inertial of the rod about these axes are `I_(A), I_(B), I_(O)` and `I_(C)` respectively.
View SolutionThe moment of inertia of thin square plate `ABCD` of uniform thickness about an axis passing through the center `O` and perpendicular to the plane of the plate is
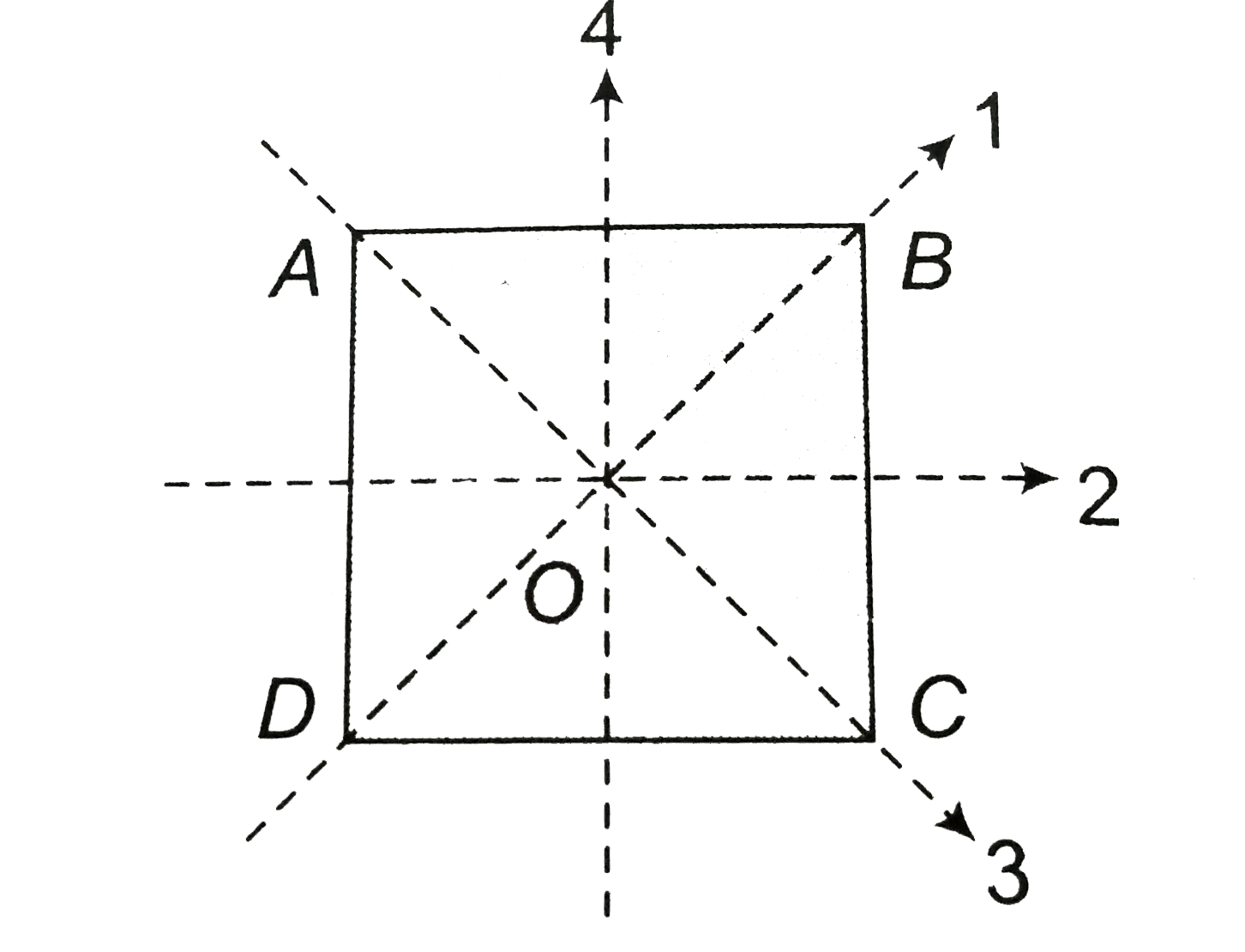
(`i`) `I_(1)+I_(2)`
(`ii`) `I_(2)+I_(4)`
(`iii`) `I_(1)+I_(3)`
(`iv`) `I_(1)+I_(2)+I_(3)+I_(4)`
where `I_(1)`, `I_(2)`, `I_(3)` and `I_(4)` are repectively moments of inertia about axes `1`, `2`, `3` and `4` which are in the plane of the plane
View SolutionMoment of inertia doesn’t depend on
distribution of particles
mass
position of axis of rotation
None of these
View SolutionFour identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
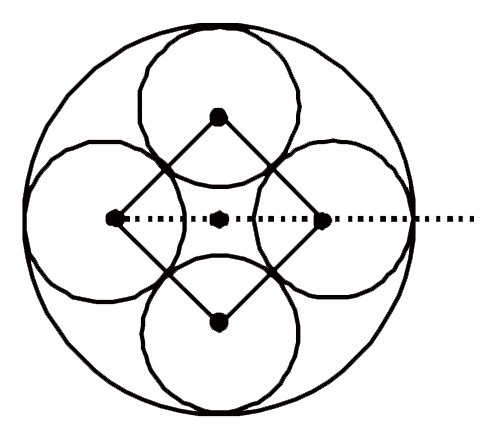
The moment of inertia of the combined ring system about the centre of ring will be
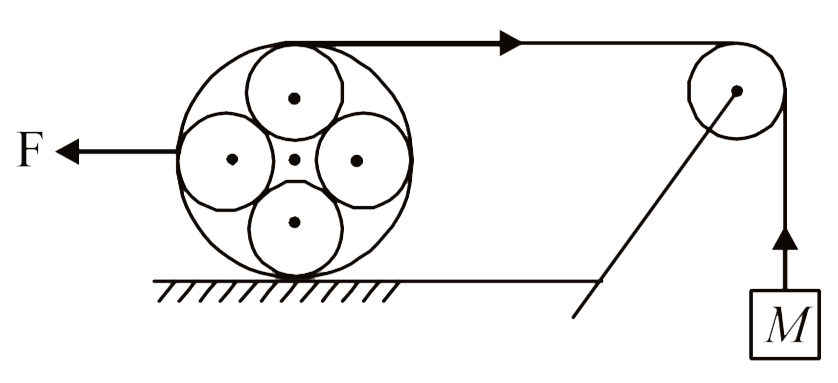
View SolutionFour identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
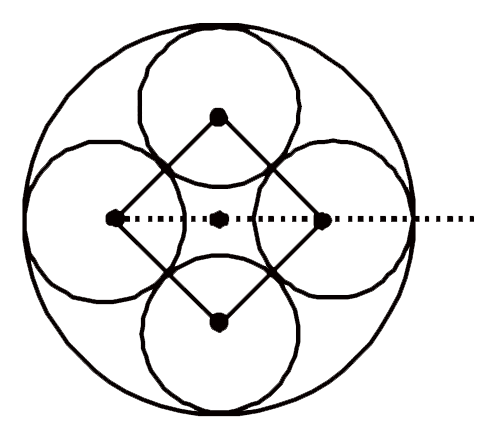
The magnitude of F is
View SolutionFour identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
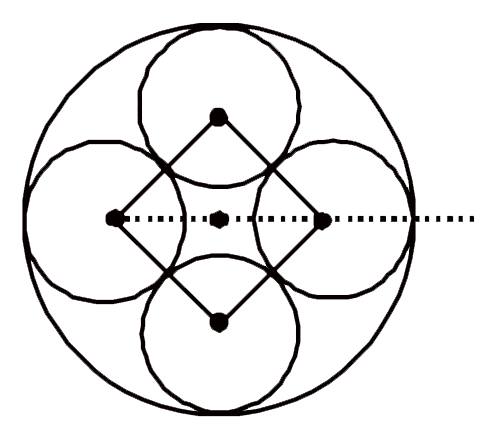
If the masses of the spheres were doubled keeping their dimensions same, the force of friction between the ring and the horizontal surface would
View SolutionStatement-1 : Radius of gyration of a body is a constant quantity.
Statement-2 : The radius of gyration of a body about an axis of rotation may be defined as the root mean square distance of the particles of the body from the axis of rotation.
View SolutionStatement-1 : Moment of inertia of a particle is same, whatever be the axis of rotation.
Statement-2 : Moment of inertia depends on mass and perpendicular distance of the particle from its axis of rotation.
View SolutionStatement-1 : If earth shrink (without change in mass) to half of its present size, length of the day would become 6 hours.
Statement-2 : When the size of the earth will change, its moment of inertia will also change.
View SolutionA uniform rod of length 2L is placed with one end in contact with the horizontal and is then inclined at an angle a to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be
View SolutionAccording to the theorem of parallel axes `I = I_("cm") + Mx^(2)`, the graph between I and x will be
View SolutionAn inclined plane makes an angle 30° with the horizontal. A solid sphere rolling down this inclined plane from rest without slipping has a linear acceleration equal to
View SolutionMoment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionOne circular ring and one circular disc, both are having the same mass and radius. The ratio of their moments of inertia about the axes passing through their centres and perpendicular to their planes, will be
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionFour thin rods of same mass M and same length l, form a square as shown in figure. Moment of inertia of this system about an axis through centre O and perpendicular to its plane is

View SolutionThe moment of inertia of a uniform circular ring, having a mass M and a radius R, about an axis tangential to the ring and perpendicular to its plane, is
View SolutionThe moment of inertia of uniform rectangular plate about an axis passing through its mid-point and parallel to its length l is (b = breadth of rectangular plate)
View SolutionThe moment of inertia of a circular ring about an axis passing through its centre and normal to its plane is `200 gm xx cm^(2)` . Then moment of inertia about its diameter is
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View SolutionIn pure rolling fraction of its total energy associated with rotation is `alpha` for a ring and `beta` for a solid sphere . Then
`(1) alpha = 1//2 " " (2) beta = 2//7 " " (3) beta = 2//5 " " (4) alpha = 1//4`
View SolutionA body is rolling down an inclined plane. Its translational and rotational kinetic energies are equal. The body is not a
(1) solid sphere (2) hollow sphere
(3) solid cylinder
(4) hollow cylinder
View SolutionTwo cylinders, one hollow (metal) and the other solid (wood) with the same mass identical dimensions are simulataneously allowed to roll without slipping down an inclined plane from the same height. The hollow cylinder will reach the bottom of the inclined plane first.
by the principle of conservation of energy, the total kinetic energies of both the cylinders are identical when they reach the bottom of the incline.
View Solution
physics questions and complete solutions for chapter ROTATIONAL MOTION of DISHA PHYSICS (HINGLISH) of Class 12