ABC is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB, IBC and ICA are the moments of inertia of the plate about AB, BC and CA repectively. Which one of the following relations is correct?
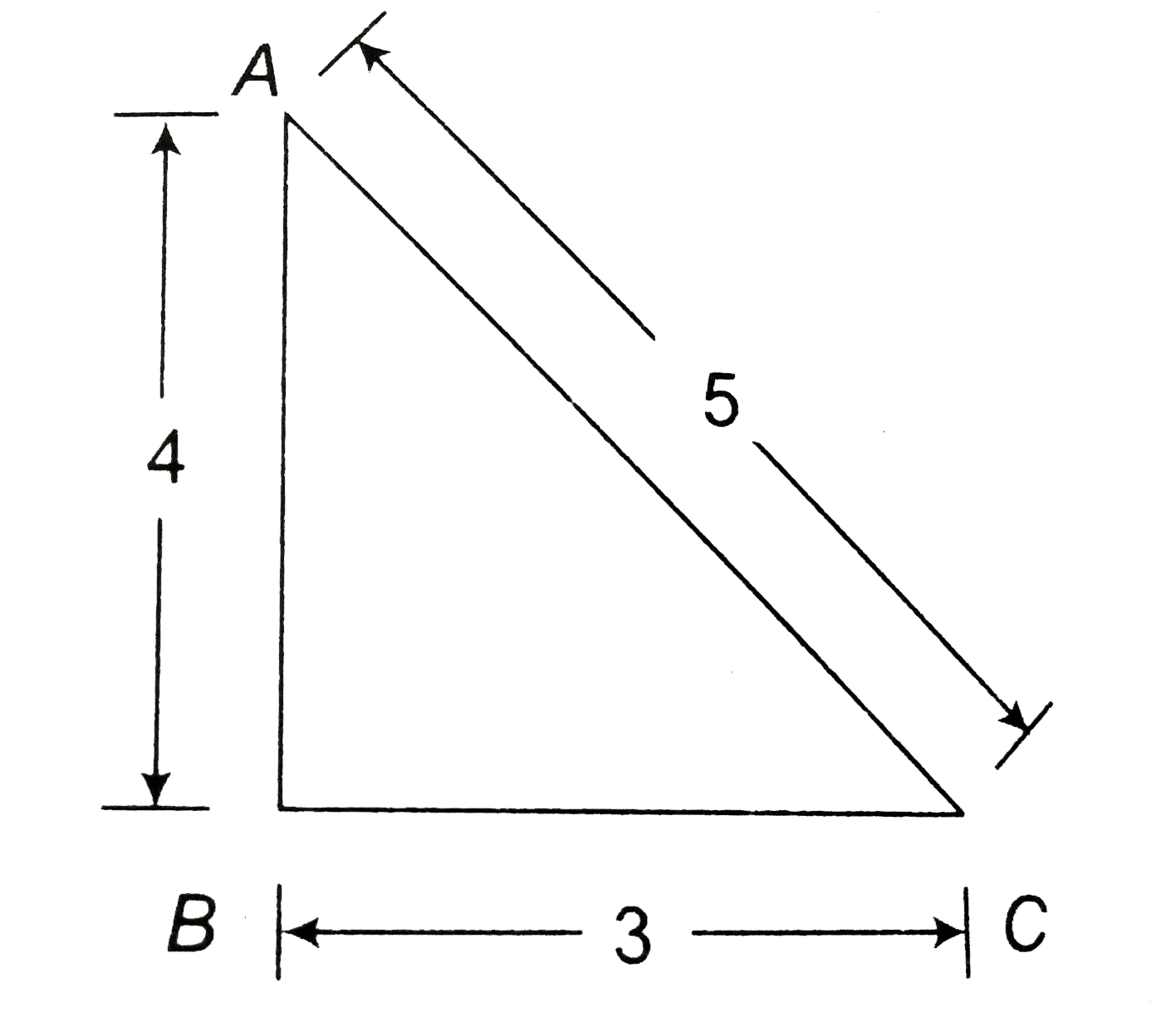
ICA is maximum
IBC>IAB
IBC>IAB
IAB+IBC=ICA
Step by step video & image solution for ABC is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. I_(AB), I_(BC) and I_(CA) are the moments of inertia of the plate about AB, BC and CA repectively. Which one of the following relations is correct? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
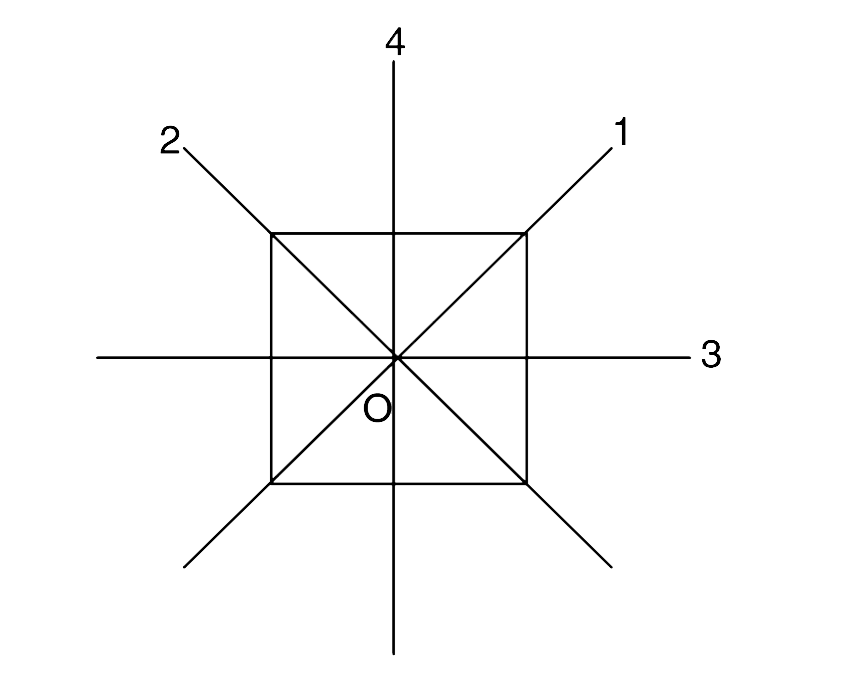
Consider a uniform square plate shown in the figure. I1,I2,I3 and I4 are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
(a) I3+I4
(b) I1+I3
(c) I2+I3
(d) 12(I1+I2+I3+I4)
 View Solution
View SolutionABC is a triangle and AD is perpendicular to BC. It is given that the lengths of AB, BC, CA are all rational numbers. Which one of the following is correct?
View Solution
Knowledge Check
- Question 1 - Select One
The ABC is a triangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB,IBC and lCA are the moments of inertia of the plate about AB, BC and CA respectively. Which one of the following relation is correct?
 AIAB+IBC=ICABICA is maximumCIAB>IBCDIBC>IAB
AIAB+IBC=ICABICA is maximumCIAB>IBCDIBC>IAB - Question 2 - Select One
ABC is a triangular plate of uniform A thickness. The sides are in the ratio shown in the figure. IAB,IBC,ICA are the moments of inertia of the plated about AB,BC and CA respectively. Which one of the following relation is correct?
 AICA is maximumBIAB>IBCCIBC>IABDIAB+IBC=ICA
AICA is maximumBIAB>IBCCIBC>IABDIAB+IBC=ICA - Question 3 - Select One
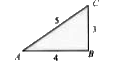
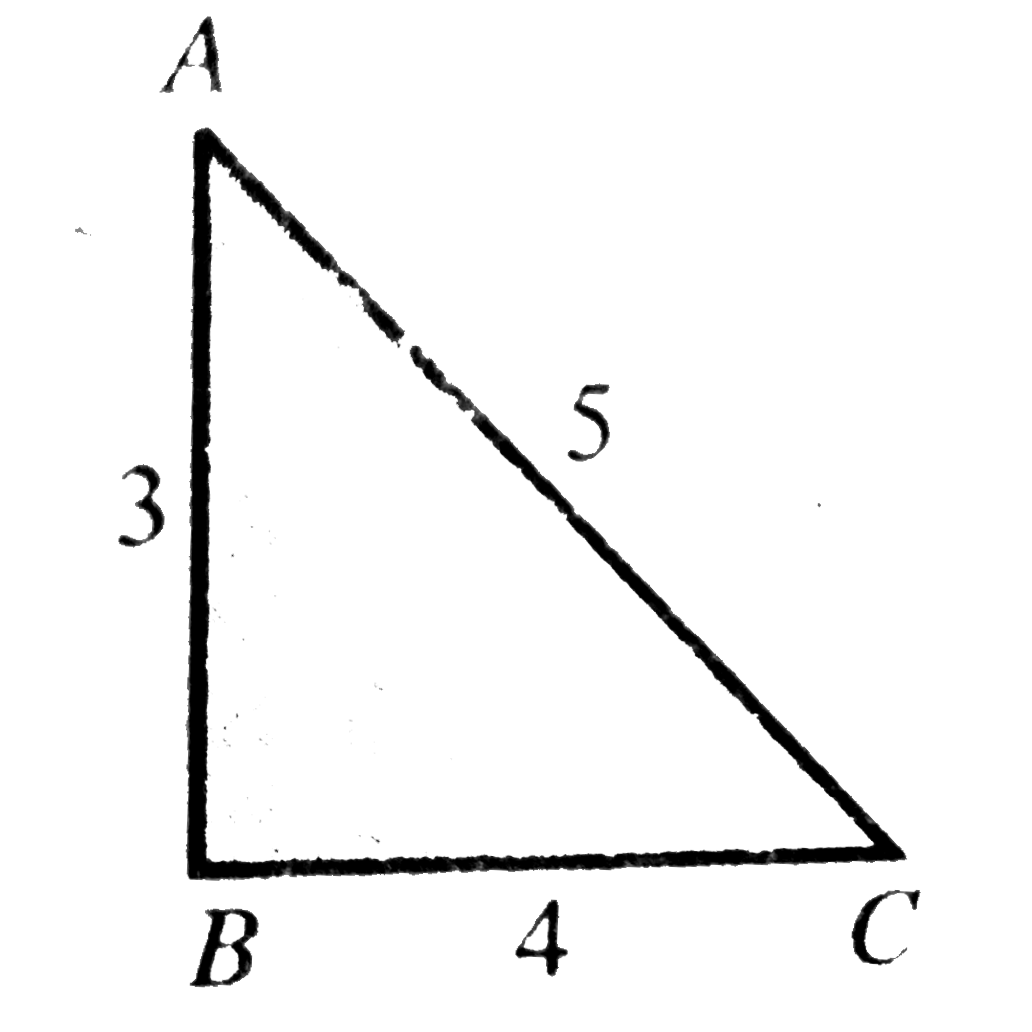
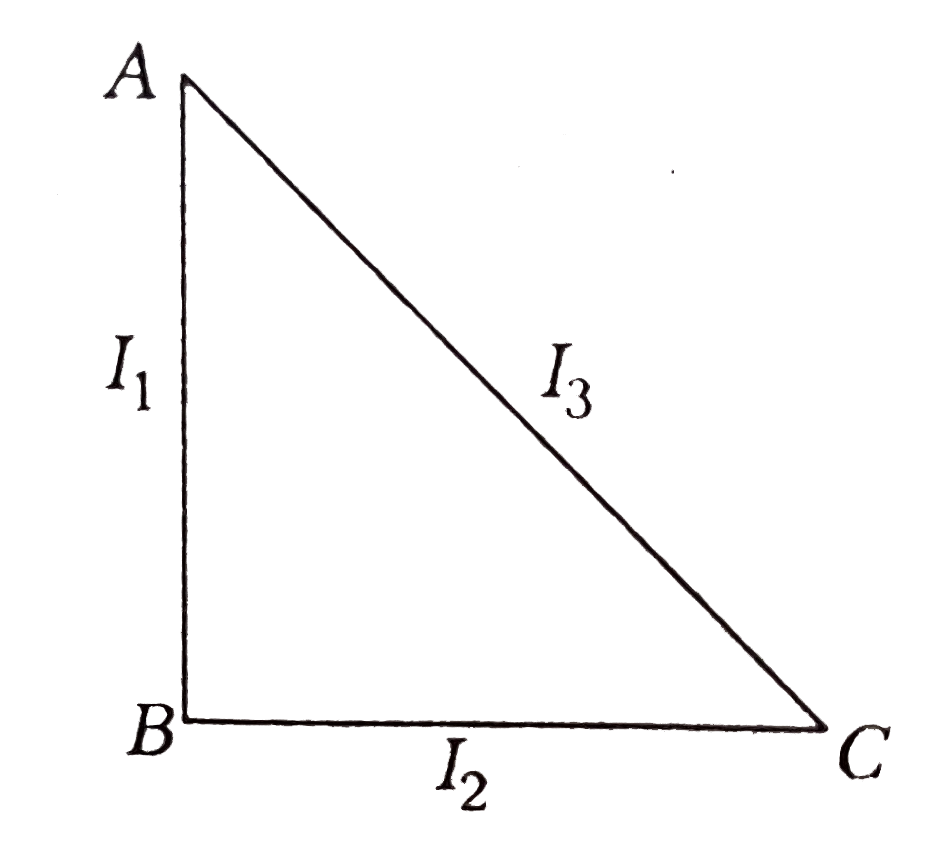
ABC is a right angled triangular plate of uniform thickness. The sides are such that AB>BC as shown in figure. I1,I2,I3 are moments of inertia about AB,BC and AC respectively. Then which of the following relations is correct?
 AI1=I2=I3BI2>I1>I3CI3<I2<I1DI3>I1>I2
AI1=I2=I3BI2>I1>I3CI3<I2<I1DI3>I1>I2
ABC is a right angled triangular plate of uniform thickness. The sides are such that AB>BC as shown in figure. I1,I2andI3 are moments of inertia about AB,BC and AC respectively. Then, which of the following relation is correct ?
 View Solution
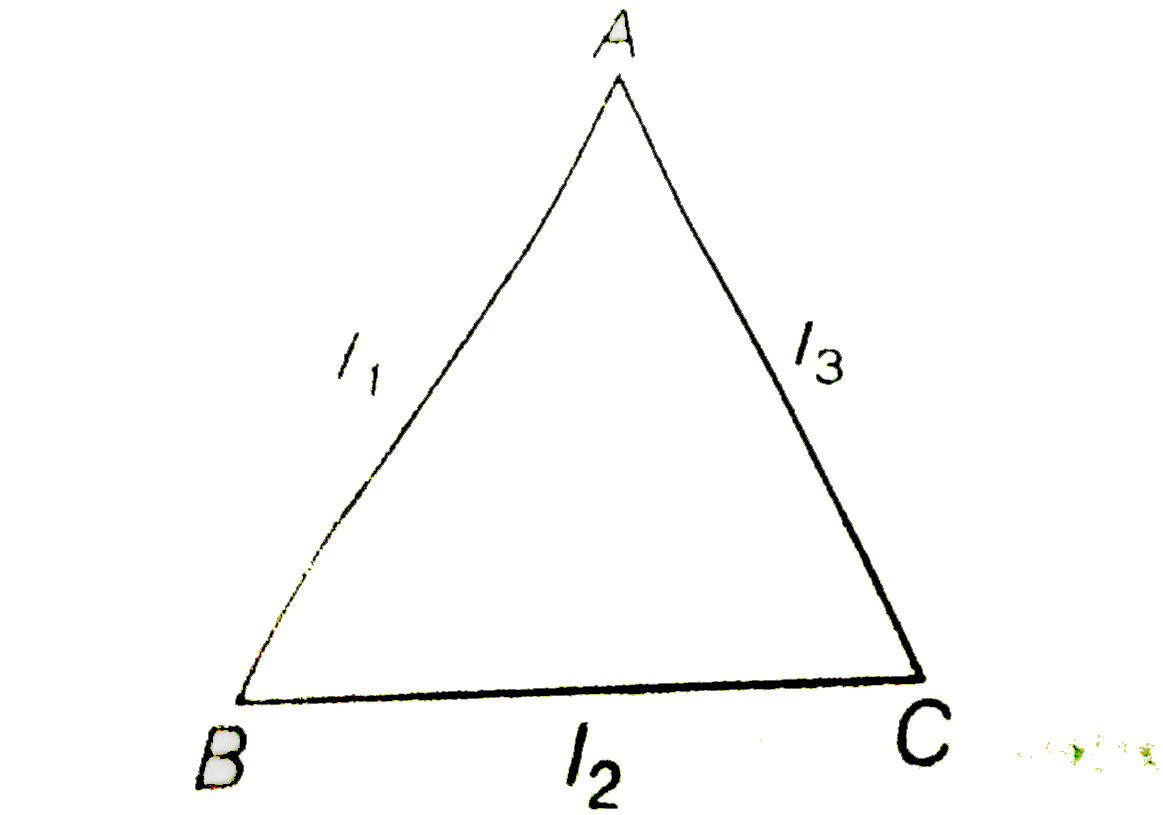
View SolutionABC is right angled triangular plane of uniform thickness The sides are such that AB gt BC as sshown in figure I1,I2,I3 are moments of inertia about AB, BC and AC, respectively.Then which of the following relations is correct?
 View Solution
View SolutionABC is a triangle in which BC = 10 cm, CA = 6 cm and AB = 8 cm, Which one of the following is a correct?
View SolutionABC is a triangle in which BC = 10 cm, CA = 6 cm and AB = 8 cm. Which one of the following is correct ?
View Solution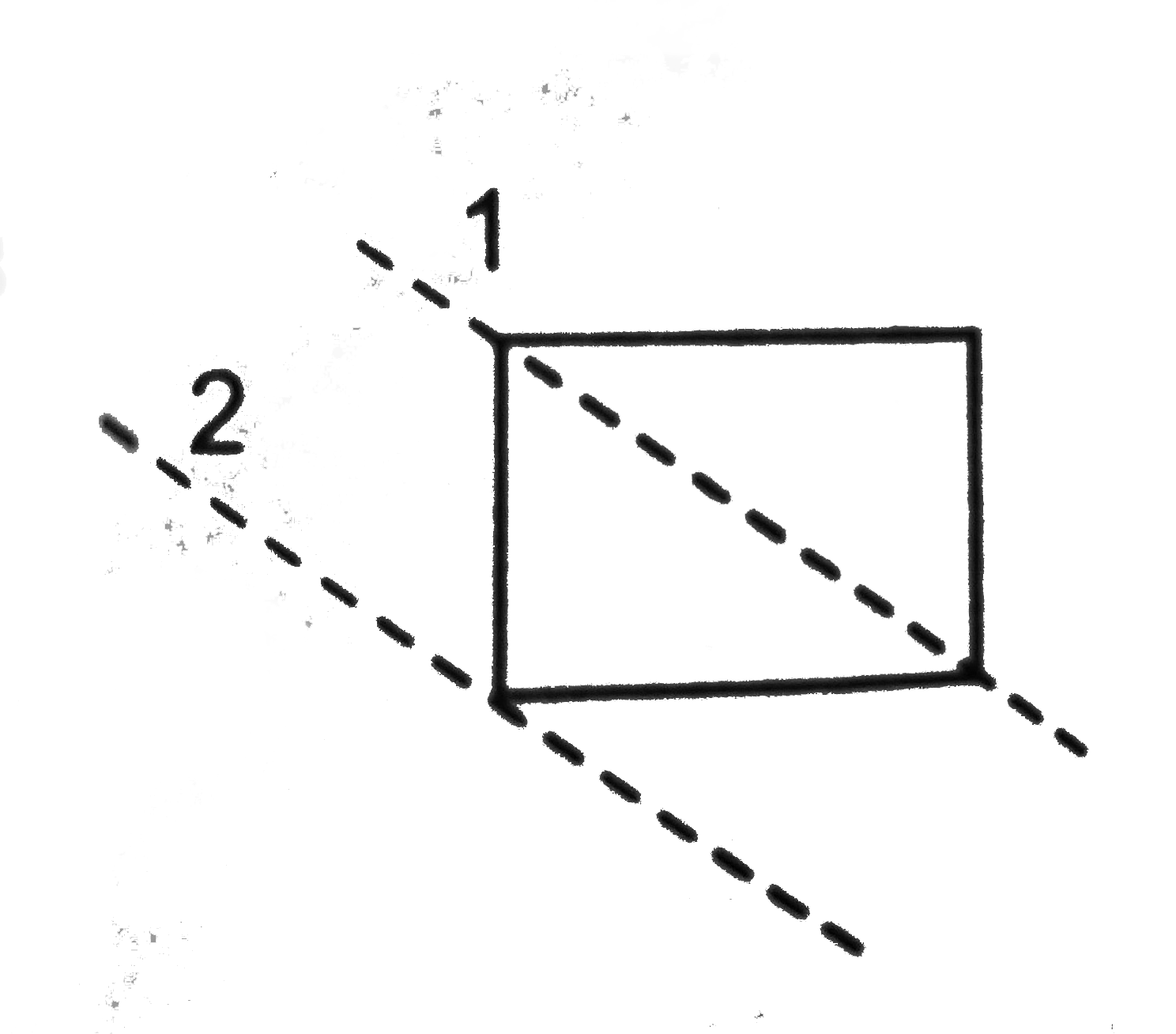
Let I1 and I2 be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I1:I2 isView Solution

