Complete Solutions to Physics of chapter THERMODYNAMICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | THERMODYNAMICS |
| DISHA | Physics |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
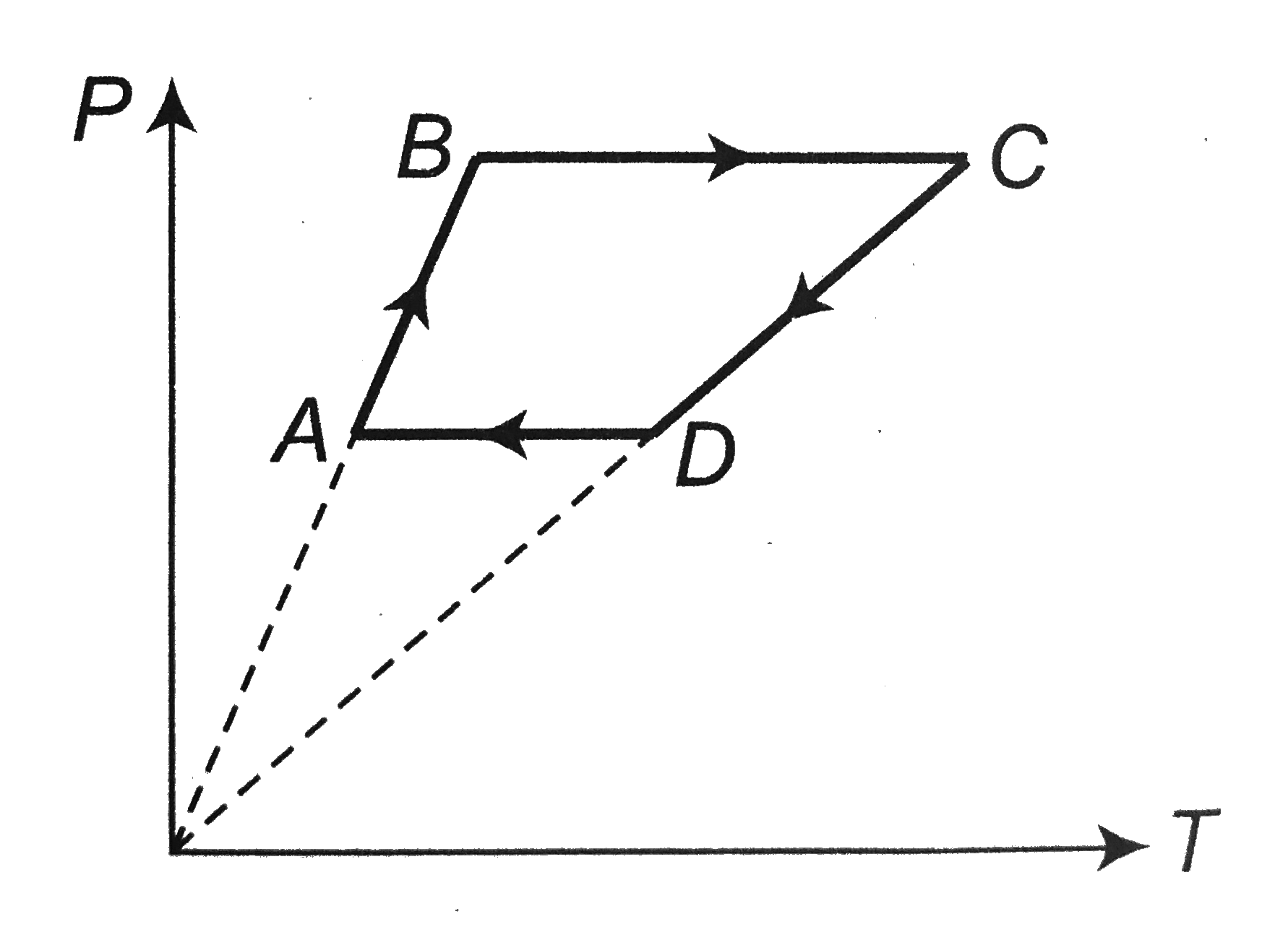
Six moles of an ideal gas performs a cycle shown in figure. If the temperature are `T_(D) = 600 K`, `T_(B) = 800 K`, `T_(C) = 2200 K` and `T_(D) = 1200 K`, the work done per cycle is
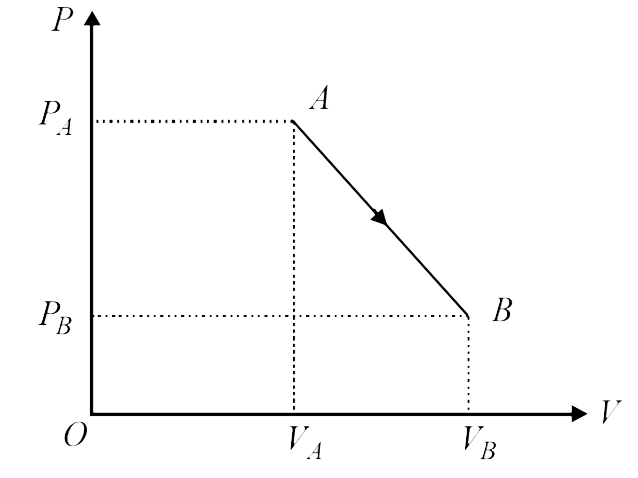
View SolutionAn ideal gas is taken from point A to the point B, as shown in the P-V diagram, keeping the temperature constant. The work done in the process is
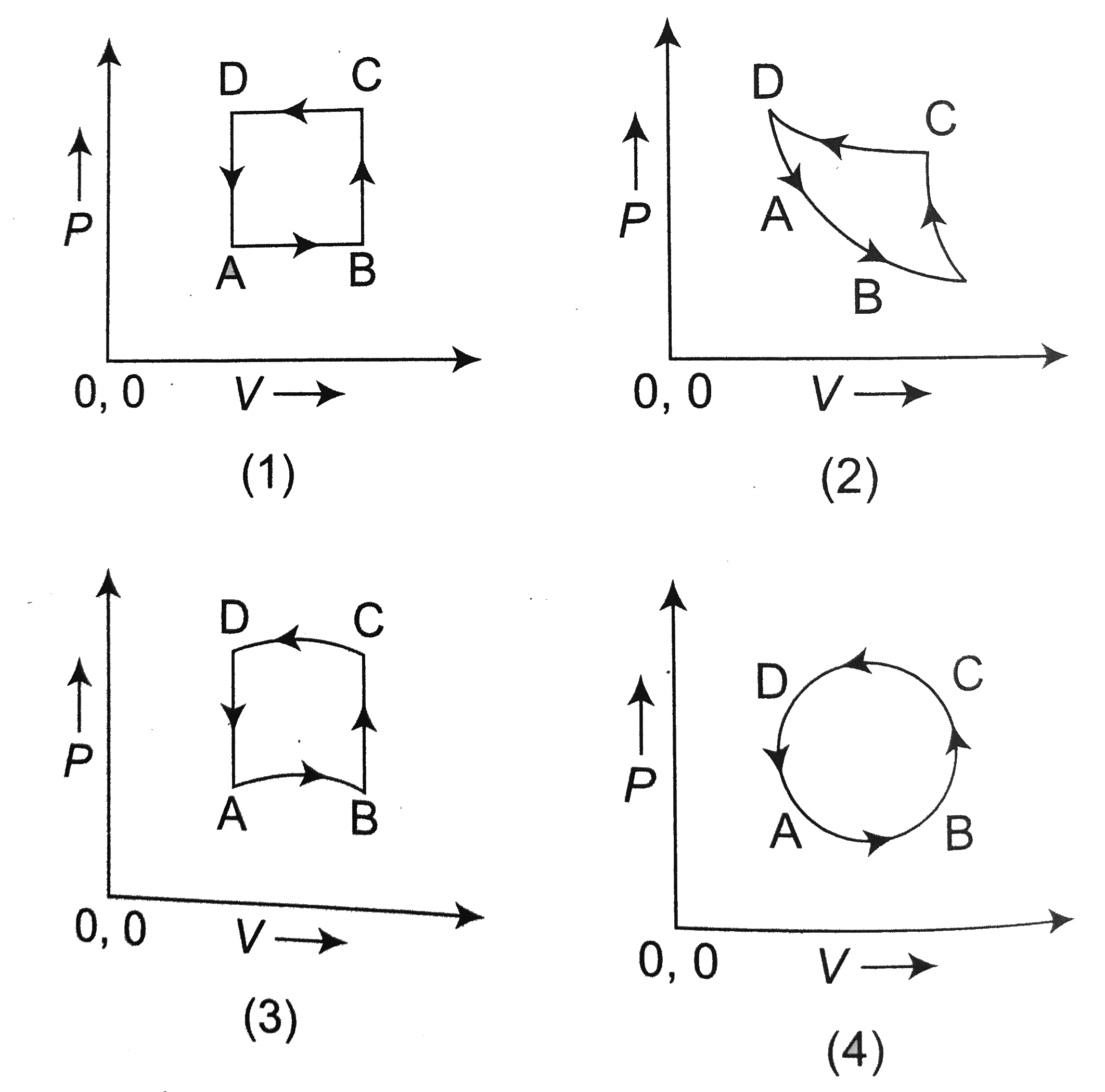
View SolutionIn following figs. Variation of volume by change of pressure is shown in Fig. A gas is taken along the path `ABCDA`. The change in internal energy of the tgas will be:
View SolutionA monoatomic ideal gas, initially at temperature `T_1,` is enclosed in a cylinder fitted with a friction less piston. The gas is allowed to expand adiabatically to a temperature `T_2` by releasing the piston suddenly. If `L_1 and L_2` are the length of the gas column before expansion respectively, then `(T_1)/(T_2)` is given by
View SolutionA gas mixture consists of 2 moles of oxygen and 4 moles of argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
View SolutionTwo Carnot engines are operated in succession. The first engine receives heat from a source at `T=800K` and rejects to sink at `T_(2)K`. The second engine receives heat rejected by the first engine and rejects to another sink at `T_(3)= 300K`. If work outputs of the two engines are equal, then find the value of `T_(2)`.
View SolutionA Carnot engine whose low temperature reservoir is at `7^(@)C` has an efficiency of `50%`. It is desired to increase the efficiency to `70%` By low many degrees should the temperature of the high temperature reservoir be increased
View SolutionAn ideal heat engine working between temperature `T_(1)` and `T_(2)` has an efficiency `eta`, the new efficiency if both the source and sink temperature are doubled, will be
View SolutionEfficiency of a Carnot engine is `50%` when temperature of outlet is `500 K`. In order to increase efficiency up to `60%` keeping temperature of intake the same what is temperature of outlet?
View SolutionA scientist says that the efficiency of his heat engine which operates at source temperature `127^(@)C` and sink temperature `27^(@)C is 26%`, then
View SolutionThe temperature of sink of Carnot engine is `27^(@)C`. Efficiency of engine is `25%`. Then temeperature of source is
View SolutionThe temperature of sink of Carnot engine is `27^(@)C`. Efficiency of engine is `25%`. Then temeperature of source is
View SolutionIn changing the state of thermodynamics from A to B state, the heat required is Q and the work done by the system is W. The change in its internal energy is
View SolutionThe first law of thermodynamics is concerned with the conservation of
View SolutionTo a system `300` joules of heat is given and it does `60` joules of work. How much does the internal energy of the system change in this process? (in joule)
View Solution110 J of heat is added to a gaseous system, whose internal energy change is 40J. Then the amount of external work done is
View SolutionFor free expansion of the gas, which of the following is true?
View SolutionIn a given process on an ideal gas, `dW=0 and dQlt0.` Then for the gas
View SolutionThe specific heat of hydrogen gas at constant pressure is `C_(P)=3.4xx10^(3)"cal"//kg^(@)C` and at constant volume is `C_(V)=2.4xx10^(3)"cal"//kg^(@)C`. If one kilogram hydrogen gas is heated from `10^(@)C` to `20^(@)C` at constant pressure the external work done on the gas to maintain it at cosntant pressure is
View SolutionWhich of the following processes are irreversible?
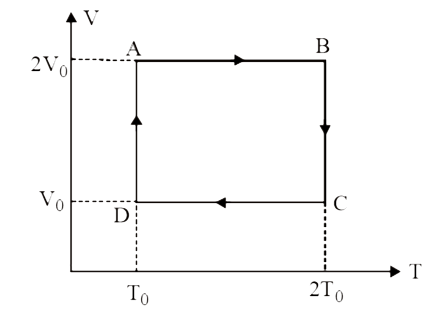
View SolutionOne mole of an ideal gas is taken through the cyclic through the cyclic process shown in the V-T diagram, where V=volume and T-absolutute temperature of the gas. Which of the following statements are correct
View SolutionV-T graph of a process of monoatomic ideal gas is shown in figure.
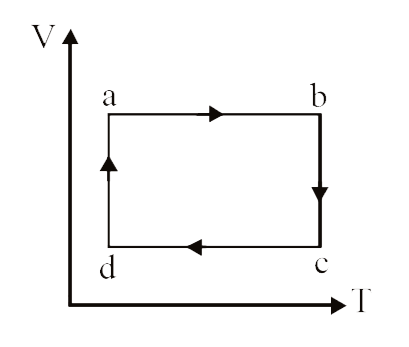
Sum of work done by the gas in process abod is-
View SolutionV-T graph of a process of monoatomic ideal gas is shown in figure.

Heat is supplied to the gas in process(s)-
View SolutionV-T graph of a process of monoatomic ideal gas is shown in figure.
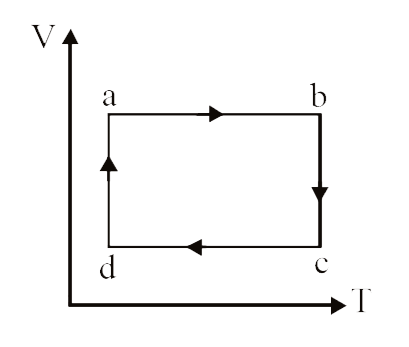
Change in internal energy of the gas is zero in process(s)-
View SolutionAssertion : It is not possible for a system, unaided by an external agency to transfer heat from a body at lower temperature to another body at higher temperature. Reason : According to Clausius statement, “ No process is possible whose sole result is the transfer of heat from a cooled object to a hotter object
View SolutionStatement-1: A room can be warmed by opening the door of a refrigerator in a closed room.
Statement-2: Head flows from lower temperature (refrigerator) to higher temperature (room).
View SolutionStatement-1: In isothermal process whole of the heat energy suppled to the body is converted into internal energy
Statement-2: According to the first law of themodynamics.
`DeltaQ=DeltaU+PDeltaV`
View SolutionFor an isothermal expansion of a perfect gas, the value of `(DeltaP)/(P)` is
View SolutionWhen an ideal gas in a cylinder was compreswsed isothermally by a piston, the work done on the gas found to be `1.5xx10^(4)` Joule. During this process about
View SolutionThe latent heat of vaporisation of water is 2240 J/gm. If the work done in the process of expansion of 1 g of water is 168 J, then increase in internal energy is
View SolutionOne mole of an ideal gas expands at a constant temperature of `300 K` from an initial volume of `10` litres to a final volume of `20` liters. The work done in expanding the gas is `(R=8.31 J// "mole"-K)` (in joules)
View SolutionThe pressure in the tyre of a car is four times the atmospheric pressure at 300 K. if this tyre suddenly bursts, Its new temperature will the `(gamma=1.4)`
View SolutionA monoatomic gas at pressure `P_(1)` and volume `V_(1)` is compressed adiabatically to `1/8th` of its original volume. What is the final pressure of gas.
View SolutionAn ideal gas at `27^(@)C` is compressed adiabatically to `8//27` of its original volume. If `gamma = 5//3`, then the rise in temperature is
View SolutionA given system undergoes a change in which the work done by the system equals to the decrease in its internal energy. The system must have undergone an
View SolutionHelium at `27^(@)C` has a volume of 8 litres. It is suddenly compressed to a volume of 1 litre. The temperature of the gas will be `[gamma=5//3]`
View SolutionOne mole of an ideal gas at an initial temperature true of `TK` does `6R` joule of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is `5//3`, the final temperature of the gas will be
View SolutionFor adiabatic process of an ideal gas the value of `(dP)/P` is equals to
View SolutionIf `300 ml` of a gas at `27^(@)` is cooled to `7^(@)` at constant pressure, then its final volume will be
View SolutionA sample of gas expands from volume `V_(1)` to `V_(2)`. The amount of work done by the gas is greatest when the expansion is
View SolutionHow much work to be done in decreasing the volume of an ideal gas by an amount of `2.4xx10^(-4)m^(3)` at constant normal pressure of `1xx10^(5) N//m^(2)`?
View SolutionOne mole of a perfect gas in a cylinder fitted with a piston has a pressure P, volume V and temperature T. if the temperature is increased by 1K keeping pressure constant, the increase in volume is
View SolutionWork done by 0.1 mole of a gas at `27^(@)C` to double its volume at constant pressure is `(R=2" cal mol"^(-1).^(@)K^(-1))`
View SolutionWhen an ideal diatomic gas is heated at constant pressure, the fraction of the heat energy supplied which increases the internal energy of the gas is
View SolutionWhen heat is given to a gas in an isothermal change, the result will be
View SolutionAn ideal gas expands isothermally from volume `V_(1)` to `V_(2)` and is then compressed to original volume `V_(1)` adiabatically. Initialy pressure is `P_(1)` and final pressure is `P_(3)`. The total work done is `W`. Then
View SolutionAn ideal gas expands in such a manner that its pressure and volume can be related by equation `PV^(2) = ` constant. During this process, the gas is
View SolutionIn the following P-V diagram two adiabatics cut two isothermals at temperature `T_(1) and T_(2)` (fig). The value of `V_(a)/V_(d)` will be
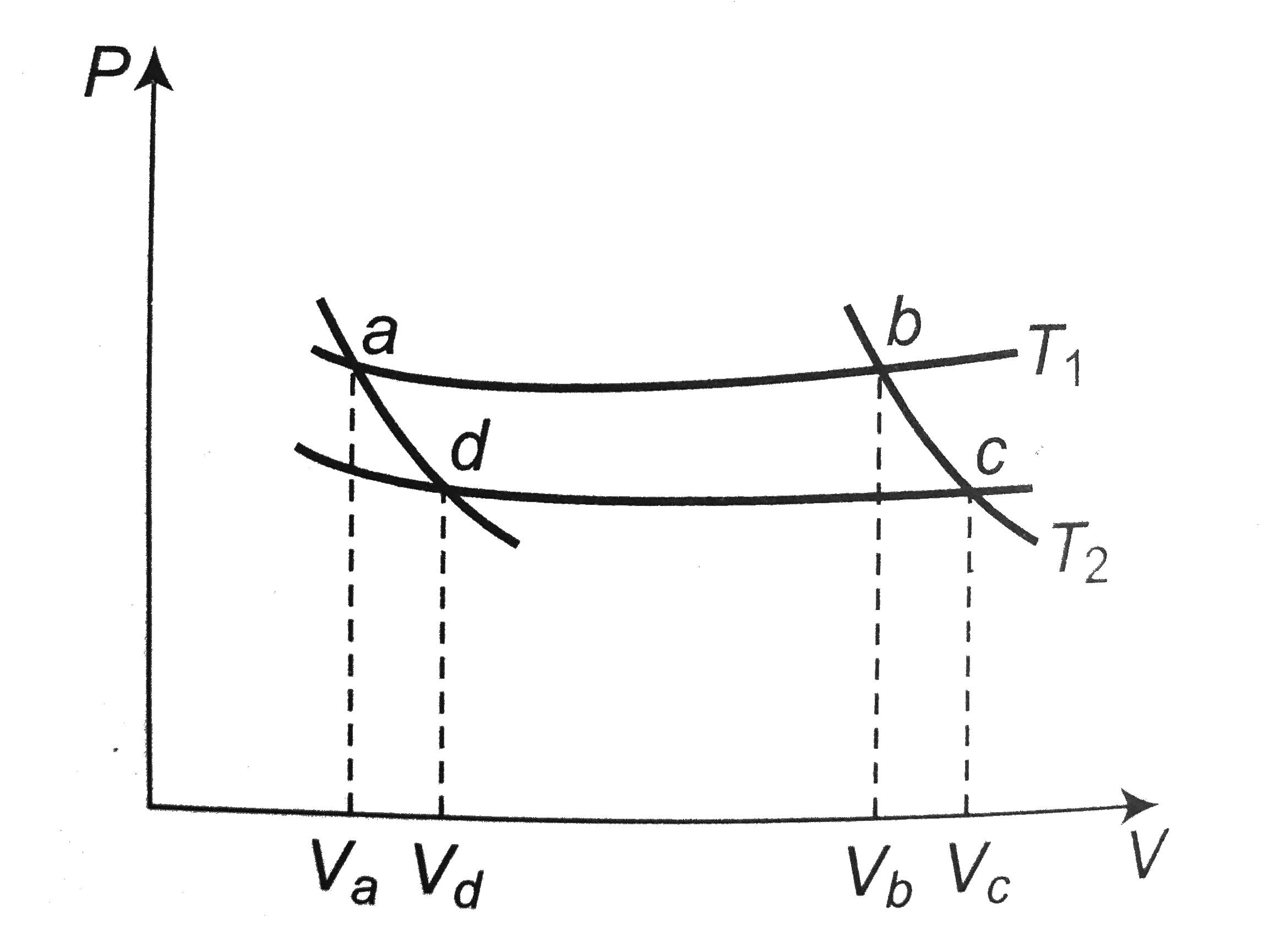
View SolutionDuring the melting of a slab of ice at 273K at atmospheric pressure,
View SolutionOne mole of an ideal monoatomaic gas is taken from `A` to `C` along the path `ABC` . The temperature of the gas at `A` is `T_(0)` . For the process `ABC` :
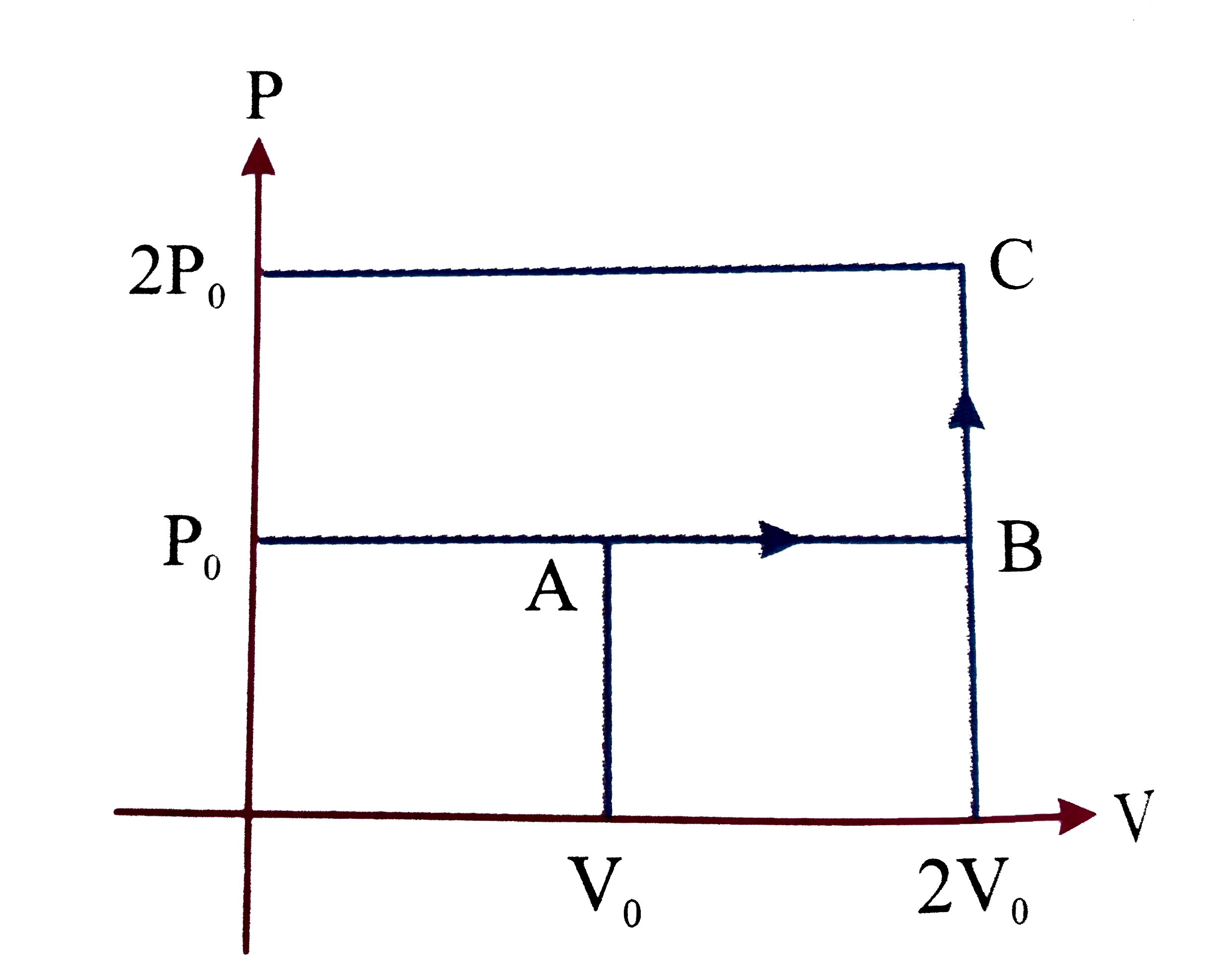
View Solution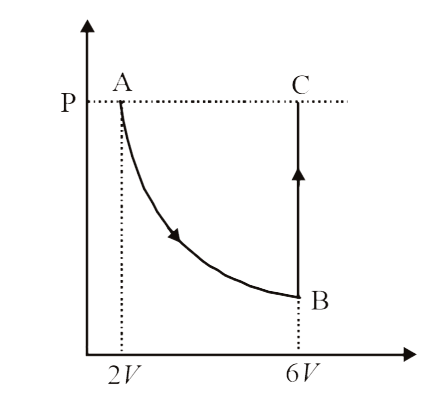
In the figure n mole of a monoatomic ideal gas undergo the process ABC as shown in the P-V diagram. The process AB is isothermal and BC is isochoric. The temperature of the gas at A is `T_(0)` total heat given to the gas during the process ABC is measured to be
Q. Temperature of the gas at C is equal to
View Solution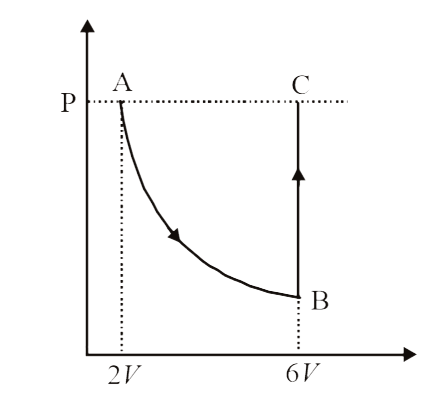
In the figure n mole of a monoatomic ideal gas undergo the process ABC as shown in the P-V diagram. The process AB is isothermal and BC is isochoric. The temperature of the gas at A is `T_(0)` total heat given to the gas during the process ABC is measured to be
Q. Heat absorbed by the gas in the process BC
View Solution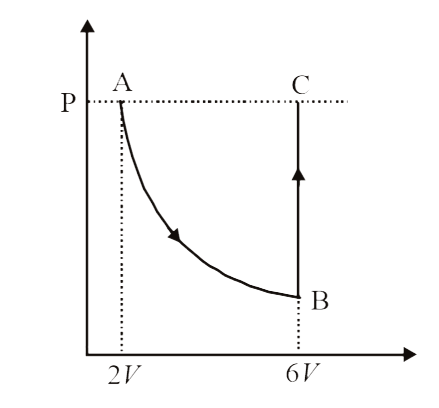
In the figure n mole of a monoatomic ideal gas undergo the process ABC as shown in the P-V diagram. The process AB is isothermal and BC is isochoric. The temperature of the gas at A is `T_(0)` total heat given to the gas during the process ABC is measured to be
Q. The average molar heat capacity of the gas in process ABC is
View SolutionAssertion: The isothermal curves intersect each other at a certain point.
Reason: The isothermal changes takes place rapidly, so the isothermal curves have very little slope.
View SolutionAssertion: In adiabatic compression, the internal energy and temperature of the system get decreased.
Reason: The adiabatic compression is a slow process.
View SolutionStatement I: The specific heat of a gas in an adiabatic process is zwero but it is infinite in an isothermal process.
Statement II: Specific heat of a gas is directly proportional to heat exchanged with the system and inversely proportional to change in termperature.
View Solution
Physics questions and complete solutions for chapter THERMODYNAMICS of DISHA PHYSICS (HINGLISH) of Class 12