Complete Solutions to physics of chapter MAGNETIC EFFECTS OF CURRENT of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC EFFECTS OF CURRENT |
| DISHA | physics |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
The magnitude of magnetic field at a point having perpendicular distance 50 mm from a long straight conducting wire carrying a current of 3A is
View SolutionA circular arc of wire of radius of curvature r subtends an angle of p/4 radian at its centre. If i current is flowing in it then the magnetic induction at its centre is -
View SolutionA current i is flowing in a conductor PQRST shaped as shown in the figure. The radius of curved part QRS is r and length of straight portions PQ and ST is very large. The magnetic field at the centre O of the curved part is -
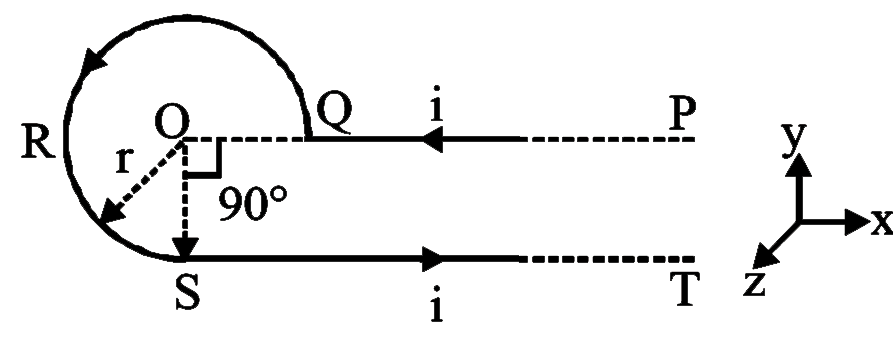
View SolutionConsider the loop PQRSP, carrying clockwise current i, shown in the figure. The magnitude of magnetic field at the centre O of the curved portion is
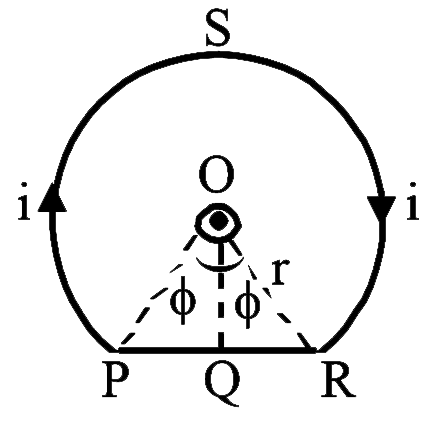
View SolutionA circular coil of 0.2 m diameter has 100 turns and carries a current of 0.1 ampere. The intensity of magnetic field at the centre of the coil is -
View SolutionFor the arrangement of two current carrying identical coils shown in the figure, the magnetic field at the center O is (N and a represent number of turns and radius of each coil)-

View SolutionA current is flowing through a conducting hollow pipe whose area of cross-section is shown in the fig. The value of magnetic induction will be zero at-

View SolutionDimensional formula of `mu_(0)` is-
View SolutionA current of 1.0 ampere is flowing in the sides of an equilateral triangle of side `4.5 xx 10^(-2)` m. Find the magnetic field at the centroid of the triangle. (Permeability constant `mu_(0) = 4pi xx 10^(-7) V-s//A-m`)
View SolutionAn air-solenoid has 500 turns of wire in its 40 cm length. If the current in the wire be 1.0 ampere then the magnetic field on the axis inside the solenoid is -
View SolutionA solenoid of length 0.2m has 500 turns on it. If `8.71 xx 10^(-6) "Weber"//m^(2)` be the magnetic field at an end of the solenoid, then the current flowing in the solenoid is –
View SolutionA circular current carrying coil has a radius R. The distance from the centre of the coil on the axis where the magnetic induction will be `(1)/(8)` th to its value at the centre of the coil, is
View SolutionThe average radius of an air cored made toroid is 0.1 m and it has 500 turns. If it carries 0.5 ampere current, then the magnetic field inside it is :
View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current `i_(1)` and `i_(2)`. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is
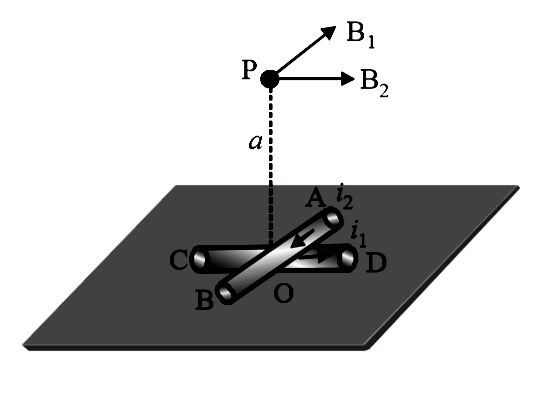
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
View SolutionThe radius of a circular loop is r and a current i is flowing in it. The equivalent magnetic moment will be
View SolutionA current of `30A` is flowing in a vertical straight wire. If the horizontal component of earths magnetic is `2xx10^(-5)T`, then the position of null point will be
View SolutionIn a region, steady and uniform electric and magnetic fields are present . These two fields are parallel to each other. A charged particle is released from rest in this region . The path of the particle will be a
View SolutionA 6.28m long wire is turned into a coil of diameter 0.2m and a current of 1 amp is passed in it. The magnetic induction at its centre will be -
View SolutionTwo long straight parallel wires carry currents I1 and I2 respectively, in the same direction (as shown). The distance between the wires is R. The magnetic field at the centre of the two wires will
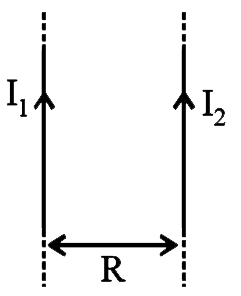
(1) `(mu_(0)(I_(1)-I_(2)))/(piR)` into the plane of paper (If `I_(1) gt I_(2)`)
(2) `(mu_(0)(I_(2)-I_(1)))/(piR)` out of the plane of paper (if `I_(2) gt I_(1)`)
(3) `(mu_(0)(I_(1)-I_(2)))/(piR^(2))` out of the plane of paper (if `I_(2) gt I_(1)`)
(4) `(mu_(0)(I_(2)-I_(1)))/(piR^(2))` into the plane of paper (if `I_(1) gt I_(2)`)
View SolutionA wire of length L carrying current I is bent into a circle of one turn. The field at the center of the coil is B1. A similar wire of length L carrying current I is bent into a square of one turn. The field at its center is B2. Then
(1) `B_(1) gt B_(2)`
(2) `B_(1) = B_(2)`
(3) `(B_(1))/(B_(2))=2`
(4) `B_(1) lt B_(2)`
View SolutionA conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation `y^(2) =2x` while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is `vec(B) - 8 hat(k)` and the current in the wire is 2A.
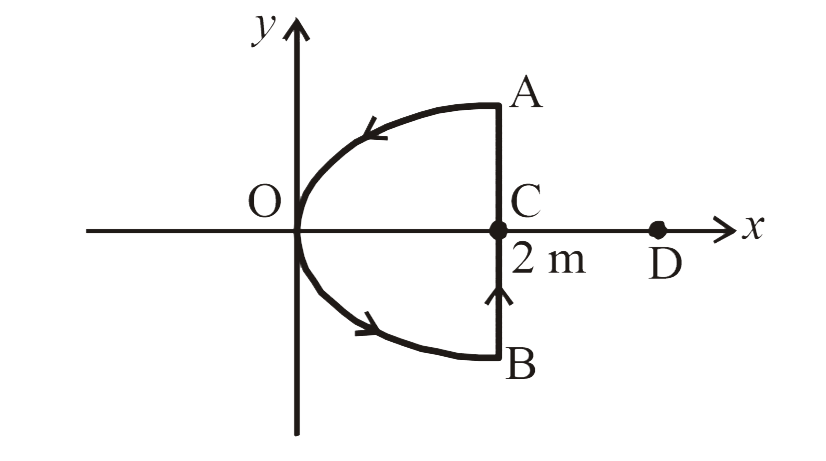
The torque on the loop will be
View SolutionA conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation `y^(2) =2x` while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is `vec(B) - 8 hat(k)` and the current in the wire is 2A.
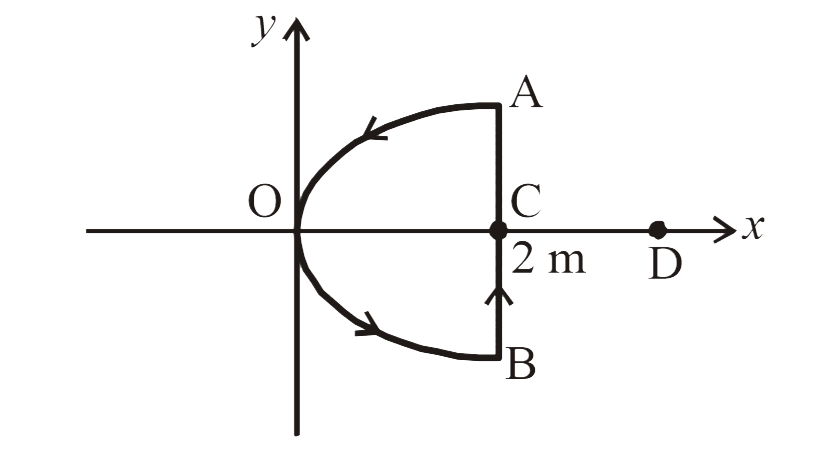
The field created by the current in the loop at point C will be
View SolutionA conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation `y^(2) =2x` while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is `vec(B) - 8 hat(k)` and the current in the wire is 2A.
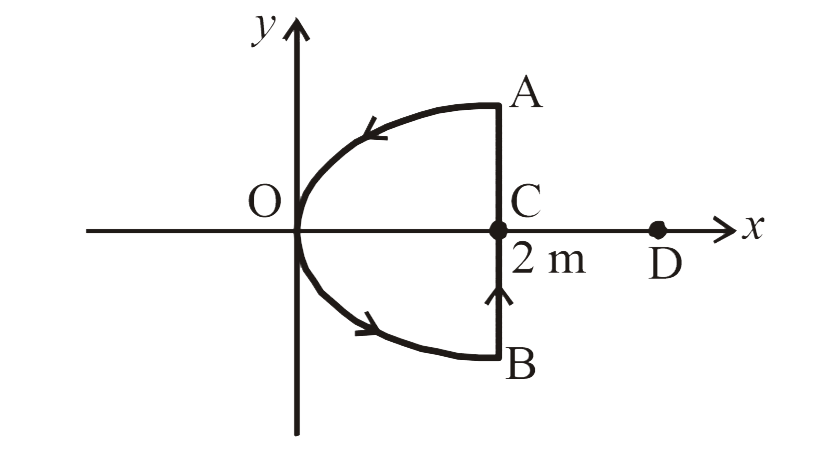
Magnetic field at point D due to segment AO of the loop is directed parallel to
View SolutionStatement -1: Cyclotron does not accelerate electron. Statement-2: Mass of the electron is very small.
View SolutionAssertion: The ion cannot move with a speed beyond a certain limit in a cyclotron.
Reason: As velocity increases time taken by ion increases.
View SolutionAssertion: If an electron, while coming vertically from outerspace, enter the earth's magnetic field, it is deflected towards west.
Reason: Electron has negative charge.
View SolutionA proton, a deuteron and an `alpha` particle are accelerated through same potential difference and then they enter a normal uniform magnetic field, the ratio of their kinetic energies will be
View SolutionA proton of energy `8 eV` is moving in a circular path in a uniform magnetic field. The energy of an alpha particle moving in the same magnetic field and along the same path will be
View SolutionAn electron is revolving in a circular path of radius `2xx10^(-10)` m with a speed of `3xx10^(6)` m/s. The magnetic field at the centre of circular path will be-
View SolutionAn `alpha` particle travels at an angle of `30^(@)` to a magnetic field 0.8 T with a velocity of `10^(5)` m/s. The magnitude of force will be-
View SolutionA beam of protons is moving horizontally towards you. As it approaches, it passes through a magnetic field directed downward. The beam deflects-
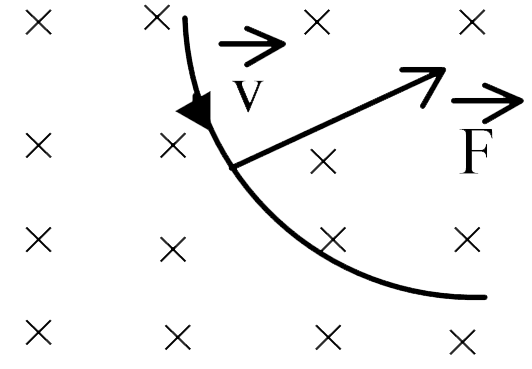
View SolutionIf a particle moves in a circular path in clockwise direction after entering into a downward vertical magnetic field. The charge on the particle is-
View SolutionIn the example above, after how much time, particle comes to the starting point for the first time. (mass of particle = m)
View SolutionA current of 2.0 amp is flowing through a wire of length 50 cm. If this wire be placed at an angle of `60^(@)` with the direction of a uniform magnetic field of `5.0 xx 10^(-4)` N/Am the force on the wire will be-
View SolutionA particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x = a to x = b. The minimum value of v required so that the particle can just enter the region x lt b is
View SolutionA particle with charge q, moving with a momentum p, enters a uniform magnetic field normally. The magnetic field has magnitude B and is confined to a region of width d, where `d lt (p)/(Bq)` , The particle is deflected by an angle q in crossing the field. Then

View SolutionAn a particle is moving in a magnetic field of `(3 hat(i) + 2 hat (j))` tesla with a velocity of `5xx10^(5) hat (i)` m/s. The magnetic force acting on the particle will be-
View SolutionIf an `alpha-` particle moving with velocity 'v' enters perpendicular to a magnetic field then the magnetic force acting on it will be-
View SolutionWhat is the net force on the square coil ?
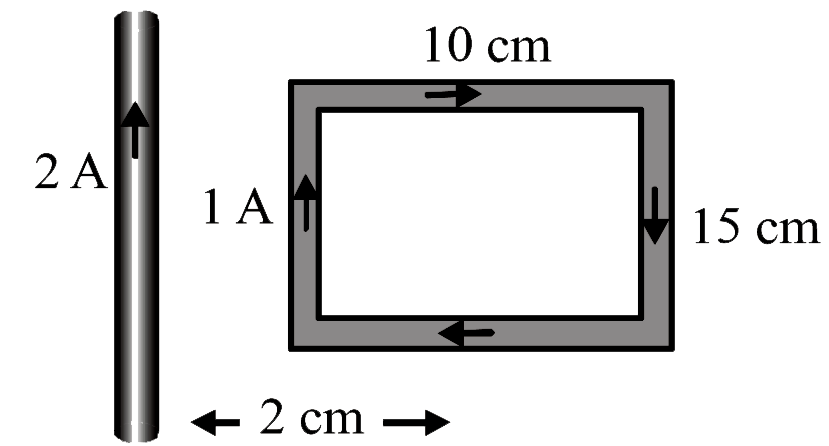
View SolutionA proton is to circulate the earth along the equator with a speed of `1.0 xx 10^(7)` m/s. The minimum magnetic field which should be created at the equator for this purpose. (The mass of proton `=1.7 xx 10^(-27)` kg and radius of earth `= 6.37 xx 10^(6)` m.) will be (in `"Wb/m"^(2)`)
View SolutionAn `alpha`-particle is describing a circle of radius 0.45 m in a field of magnetic induction `1.2 "weber/m"^(2)`. The potential difference required to accelerate the particle, (The mass of a-particle is `6.8 × 10^(-27)` kg and its charge is `3.2 xx 10^(-19)` coulomb.) will be —
View SolutionAn electron beam passes through a magnitic field of `2xx10^(-3) "weber"//m^(2)` and an electric field of `1.0 xx 10^(4) "volt/m"` both acting simultaneously. If the electric field is removed, what will be the radius of the electron path ?
View SolutionA straight horizontal copper wire carries a current i = 30 A. The linear mass density of the wire is 45 g/m. What is the magnitude of the magnetic field needed to balance its weight?
View SolutionA 1m long conducting wire is lying at right angles to the magnetic field. A force of 1 kg. wt is acting on it in a magnetic field of 0.98 tesla. The current flowing in it will be-
View SolutionIn the fig the two parallel wires PQ and ST are at 30 cm apart. The currents flowing in the wires are according to fig. The force acting over a length of 5m of the wires is-

(1) `5xx10^(-4) N`
(2) attraction
(3) `5xx10^(-8) N`
(4) repulsion
View SolutionA beam of protons enters a uniform magnetic field of 0.3 tesla with a velocity of `4xx10^(5)` m/s at an angle of 60º to the field. Then, (Mass of the proton `=1.7 xx10^(-27)` kg.)
(1) the radius of the helical path is `1.226 xx 10^(-2)` m
(2) the pitch of the helix is `4.45 xx 10^(-2)` m
(3) the radius of the helical path is `1.226 xx 10^(-3)` m
(4) the pitch of the helix is `4.45xx10^(-4)` m
View SolutionA charge particles q enters in a magnetic field `vec(B)=y hat(i) + x hat (j)` with the velocity `vec(v)= x hat (i) y hat (j)` . Neglect any force other than magnetic force. Now answer the following question.
When particle arrives at any point P (2, 2) then force acting on it, will be –
View SolutionA charge particles q enters in a magnetic field `vec(B)=y hat(i) + x hat (j)` with the velocity `vec(v)= x hat (i) y hat (j)` . Neglect any force other than magnetic force. Now answer the following question.
Magnetic force F acting on charge is proportional to –
View SolutionA charge particles q enters in a magnetic field `vec(B)=y hat(i) + x hat (j)` with the velocity `vec(v)= x hat (i) y hat (j)` . Neglect any force other than magnetic force. Now answer the following question.
Which of the following is true for the direction of magnetic force ?
View SolutionStatement -1 : If two long wires, hanging freely are connected to a battery in series, they come closer to each other. Statement -2 : Force of repulsion acts between the two wires carrying current.
View SolutionStatement - 1 : For a charged particle to pass through a uniform electro-magnetic field without change in velocity, its velocity vector must be perpendicular to the magnetic field. Statement - 2 : Net Lorentz force on the particle is given by `vec(F)=q[vec(E)+vec(v)xxvec(B)]`.
View SolutionStatement - 1 : If an electron is not deflected while passing through a certain region of space, then only possibility is that there is no magnetic region. Statement - 2 : Magnetic force is directly proportional to the magnetic field applied.
View SolutionA circular coil of radius `4 cm` and of `20` turns carries a current of `3` amperes. It is placed in a magnetic field of intensity of `0.5 weber//m^(2)`. The magnetic dipole moment of the coil is
View SolutionA circular coil of radius 4 cm has 50 turns. In this coil a current of `2 A` is flowing. It is placed in a magnetic field of `0.1 "weber"//m^(2)`. The amount of work done is rotation it through `180 ^(@)` from its equilibrium position will be
View SolutionThe deflection in a moving coil galvanometer is
View SolutionA moving coil galvanometer has `N` numbr of turns in a coil of effective area `A`, it carries a current `I`. The magnetic field `B` is radial. The torque acting on the coil is
View SolutionA current carrying loop is free to turn in a uniform magnetic field.The loop will then come into equilibrium when its plane is inclined at
View SolutionA 100 turns coil shown in figure carries a current of 2 amp in a magnetic field `B=0.2 Wb//m^(2)`. The torque acting on the coil is
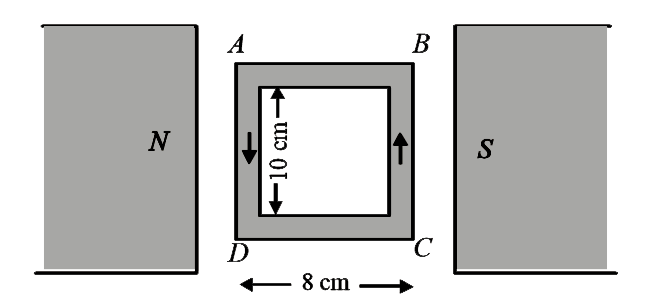
View SolutionA rectangular coil `20cmxx20cm` has `100` turns and carries a current of `1 A`. It is placed in a uniform magnetic field `B=0.5 T` with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA circular loop of area `0.01 m^(2)` carrying a current of `10 A`, is held perpendicular to a magnetic field of intensity `0.1 T`. The torque acting on the loop is
View SolutionThe magnetic moment of a circular coil carrying current is
View SolutionWhat is the shape of magnet in moving coil galvanometer to make the radial magnetic field ?
View SolutionCurrent `i` is carried in a wire of length `L`. If the wire is turned into a circular coil, the maximum magnitude of torque in a given magnetic field `B` will be
View SolutionIn ballistic galvanometer, the frame on which the coil is wound is non-metallic. It is
View SolutionA solenoid of length 0.4 m and having 500 turns of wire carries a current of 3 amp. A thin coil having 10 turns of wire and of radius 0.01 m carries a current of 0.4 amp. The torque (in Nm) required to hold the coil in the middle of the solenoid with its axis perpendicular to the axis of the solenoid is (`mu_(0) = 4pi xx 10^(-7)` V-s/A-m)
View SolutionIf an electron is moving with velocity v in an orbit of radius r in a hydrogen atom, then the equivalent magnetic moment is
View SolutionIn a moving coil galvanometer, the deflection of the coil q is related to the electrical current i by the relation
View SolutionA thin circular wire carrying a current I has a magnetic moment M. The shape of the wire is changed to a square and it carries the same current. It will have a magnetic moment
View SolutionA ring of radius `R`, made of an insulating material carries a charge `Q` uniformly distributed on it. If the ring rotates about the axis passing through its centre and normal to plane of the ring with constant angular speed `omega`, then the magnitude moment of the ring is
View SolutionThe `(tau - theta)` graph for a current carrying coil placed in a uniform magnetic field is
View SolutionA rectangular loop carrying a current i is placed in a uniform magnetic field B. The area enclosed by the loop is A. If there are n turns in the loop, the torque acting on the loop is given by
View SolutionFour wires each of length `2.0` meters area bent into four loops `P,Q,R` and `S` and then suspended into uniform magnetic field. Same current is passed in each loop. Which statement is correct?

View SolutionThe sensitivity of a moving coil galvanometer can be increased by
(1) decreasing the couple per unit twist of the suspension
(2) increasing the number of turns in the coil
(3) decreasing the area of the coil
(4) decreasing the magnetic field
View SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field `vec(B) = (2 hat(i) - 3 hat(j) +hat (k))T` is present in the region. Then, find
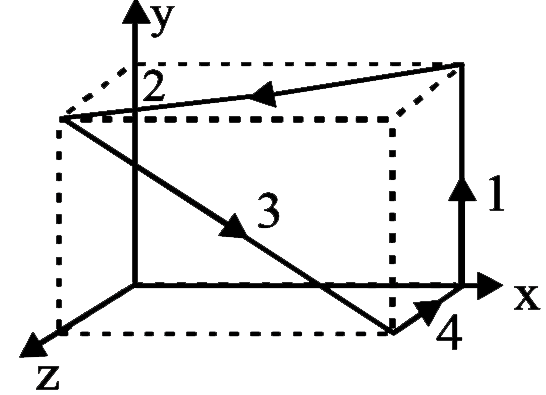
The net force on the loop
View SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field `vec(B) = (2 hat(i) - 3 hat(j) +hat (k))T` is present in the region. Then, find
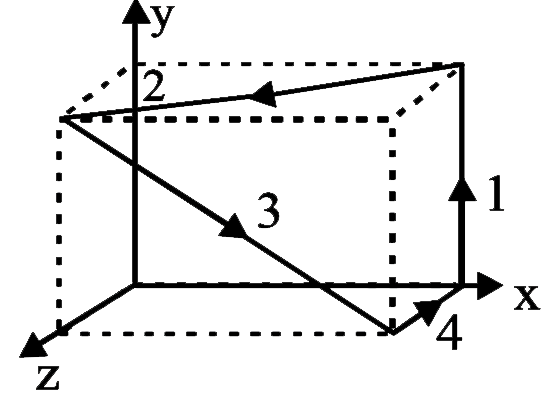
The magnetic moment vector of the loop.
View SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field `vec(B) = (2 hat(i) - 3 hat(j) +hat (k))T` is present in the region. Then, find
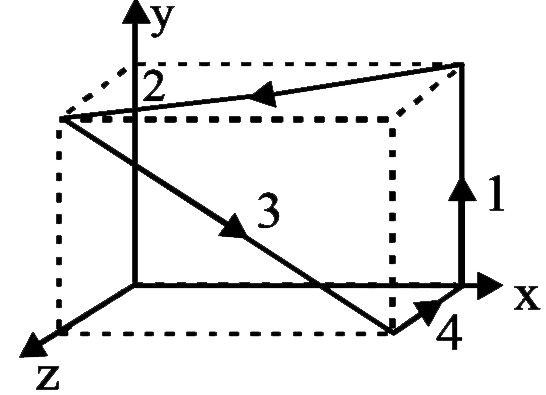
The net torque on the loop
View SolutionAssertion: The coil is bound over the metallic fram in moving coil galvanometer.
Reason: The metallic fram help in making steady deflected without any oscillation.
View SolutionAssertion: Torque on the coil is the maximum, when coil is suspended in a radial magentic field.
Reason: The torque tends to rotates the coil on its own axis.
View SolutionStatement-1 : A current carrying loop placed in equilibrium in a uniform magnetic field starts oscillating when disturbed from equilibrium. Statement-2 : A system when disturbed slightly from stable equilibrium oscillates
View Solution
physics questions and complete solutions for chapter MAGNETIC EFFECTS OF CURRENT of DISHA PHYSICS (HINGLISH) of Class 12