A straight horizontal copper wire carries a current i = 30 A. The linear mass density of the wire is 45 g/m. What is the magnitude of the magnetic field needed to balance its weight?
147 G
441 G
14.7 G
0 G
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the Problem
We need to find the magnitude of the magnetic field (B) required to balance the weight of a straight horizontal copper wire carrying a current of 30 A. The linear mass density of the wire is given as 45 g/m.
Step 2: Convert Linear Mass Density
Convert the linear mass density from grams per meter to kilograms per meter for consistency in SI units:
Linear mass density=45g/m=45×10−3kg/m=0.045kg/m
Step 3: Calculate the Weight of the Wire
The weight (W) of a length (L) of the wire can be calculated using the formula:
W=M⋅g
where M is the mass of the wire and g is the acceleration due to gravity (approximately 9.8m/s2). The mass M can be expressed in terms of linear mass density (μ) and length (L):
M=μ⋅L
Thus, the weight becomes:
W=μ⋅L⋅g
Step 4: Calculate the Magnetic Force
The magnetic force (F) acting on the wire due to the magnetic field is given by:
F=i⋅L⋅B
where i is the current flowing through the wire.
Step 5: Set the Forces Equal
To balance the weight of the wire with the magnetic force, we set the two forces equal:
i⋅L⋅B=μ⋅L⋅g
Step 6: Cancel Length (L)
Since L appears on both sides of the equation, we can cancel it out (assuming L≠0):
i⋅B=μ⋅g
Step 7: Solve for Magnetic Field (B)
Now, we can solve for the magnetic field B:
B=μ⋅gi
Step 8: Substitute Values
Substituting the known values into the equation:
B=0.045kg/m⋅9.8m/s230A
Step 9: Calculate B
Calculating the value:
B=0.44130≈0.0147T
Step 10: Convert to Gauss
Since 1T=104Gauss:
B≈0.0147T=1.47Gauss
Final Answer
The magnitude of the magnetic field needed to balance the weight of the wire is approximately 1.47 Gauss.
---
We need to find the magnitude of the magnetic field (B) required to balance the weight of a straight horizontal copper wire carrying a current of 30 A. The linear mass density of the wire is given as 45 g/m.
Convert the linear mass density from grams per meter to kilograms per meter for consistency in SI units:
Linear mass density=45g/m=45×10−3kg/m=0.045kg/m
The weight (W) of a length (L) of the wire can be calculated using the formula:
W=M⋅g
where M is the mass of the wire and g is the acceleration due to gravity (approximately 9.8m/s2). The mass M can be expressed in terms of linear mass density (μ) and length (L):
M=μ⋅L
Thus, the weight becomes:
W=μ⋅L⋅g
The magnetic force (F) acting on the wire due to the magnetic field is given by:
F=i⋅L⋅B
where i is the current flowing through the wire.
To balance the weight of the wire with the magnetic force, we set the two forces equal:
i⋅L⋅B=μ⋅L⋅g
Since L appears on both sides of the equation, we can cancel it out (assuming L≠0):
i⋅B=μ⋅g
Now, we can solve for the magnetic field B:
B=μ⋅gi
Substituting the known values into the equation:
B=0.045kg/m⋅9.8m/s230A
Calculating the value:
B=0.44130≈0.0147T
Since 1T=104Gauss:
B≈0.0147T=1.47Gauss
The magnitude of the magnetic field needed to balance the weight of the wire is approximately 1.47 Gauss.
Topper's Solved these Questions
Similar Questions
A straight wire, of length L, carrying a current I, stays suspended horizontally in mid air in a region where there is a uniform magnetic field →B. The linear mass density of the wire is λ. Obtain the magnetic of this magnetic field.
View SolutionA straight wire of length L and carrying a curretn I stays suspended horizontally in mid air in a region where there is a uniform magnetic field →B. The linear mass density of the wire is λ. Obtain the magnitude and direction of this magnitude field.
View Solution
Knowledge Check
- Question 1 - Select One
Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current I1 of 6.00A into the plane of the paper.

What is the magnitude of the net field at S?A4.1×10−6TB1.6×10−6TC3.2×10−6TD2.1×10−6T - Question 2 - Select One
Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current I1 of 6.00A into the plane of the paper.
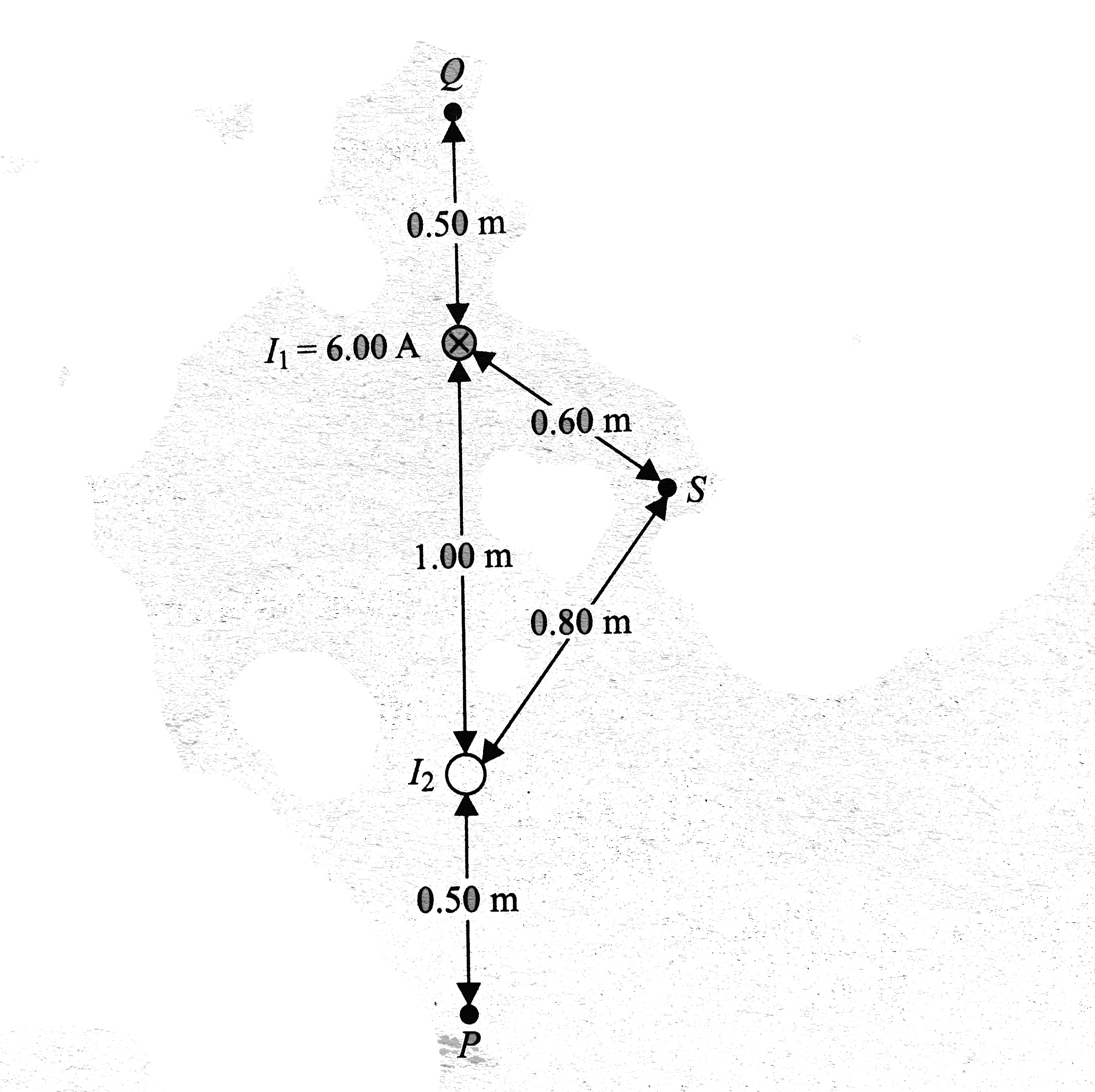
What is the magnitude of the net field at Q?A2.13×10−6TB4.26×10−6TC1.21×10−6TD5.30×10−6T - Question 3 - Select One
A wire carries current toward the north. In the region beneath this wire, What is the direction of the magnetic field due to the current ?
ANorthwardBSouthwardCEastwardDWestward
A straight wire of mass 400 g and length 2m carries a current of 2A. It is suspended in mid air by a uniform horizontal field B. What is the magnitude of the magnetic field ?
 View Solution
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA copper wire of diameter 1.6 mm carries a current of 20A. Find the maximum magnitude of the magnetic field (vec B)due to this current.
View SolutionA straight wire carrying a current 10A is bent into a semicircular arc of radius 5cm. The magnitude of magnetic field at the center is
View SolutionA horizontal wire of length 0.5m carries a current of 5A. If the mass of the wire is 10mg, the minimum magnetic field required to support the weight of the wire is (g=10m/g2)
View Solution

