Complete Solutions to Exercise-1 of chapter MOTION IN A STRAIGHT LINE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| DISHA PUBLICATION | Exercise-1 |
| Number Of Questions | 70 |
| Academic Year | 2023-24 |
The location of a particle is changed. What can we say about the displacement and distance covered by the particle?
View SolutionThe displacement-time graph for two particles A and B are straight lines inclined at angles of `30^(@)` and `60^(@)` with the time axis. The ratio of velocities of `V_(A) :V_(B)` is
View SolutionA body moves in a straight line along Y-axis. Its distance y in metre) from the origin is given `y = 8t -3t^(2).` The average speed in the time interval from `t =0` second to `t =1` second is
View SolutionFor the velocity -time graph shown in the figure below the distance covered by the body in the last two seconds of its motion is what fracting of the total distance travelled by it in all the seven seconds?

View SolutionA car travels from A to B at a speed of `20 km//hr` and returns at a speed of `30 km//hr`. The average speed of the car for the whole journey is
View SolutionA man leaves his house for a cycle ride. He comes back to his house after half-an-hour after covering a distance of one km. What is his average velocity for the ride?
View SolutionThe displacement `x` of a body varies with time `t` as `x= -2/3 t^(2)+16 t+2`. The body will come to rest after :
View SolutionThe coordinates of a moving particle at time t are given by `x=ct^(2)` and `y=bt^(2)`. The speed of the particle is given by :-
View SolutionTwo particles A and B are connected by a rigid rod AB. The rod slides along perpendicular rails as shown here. The velocity of A to the left is 10 m/s. What is the velocity of B when angle `alpha= 60^(@)` ?

View SolutionA bird files with a speed of 10 km/h and a car moves with uniforms speed of 8 km/h .both start from B towrd A (BA=40km) at the same insatnt . The bird having reached A files back immediately to meet the apporaching car. As shown as it reach the car If fiels back to A. The birds repeats this till both the car and the car and the bird reach A simultaneously .The total distancecovered by the bird is 15`psi` km. Find the value of `psi`
View SolutionThe velocity of a particle is `v = v_(0) + g t + ft^(2)`. If its position is ` x=0 ` at ` t= 0 `, then its displacement after unit time `( t = 1 )` is
View SolutionA particle located at `x = 0` at time `t = 0`, starts moving along with the positive ` x-direction` with a velocity 'v' that varies as ` v = a sqrt(x)`. The displacement of the particle varies with time as
View SolutionThe co-ordinates of a moving particle at anytime 't' are given by ` x = alpha t^(3) and y = beta t^(3)`. The speed of the particle at time 't' is given by
View SolutionThe displacement 'x' (in meter) of a particle of mass 'm' (in kg) moving in one dimension under the action of a force is released to time 't' (in sec) by `t = sqrt(x) + 3`. The displacement of the particle when its velocity is zero will be.
View SolutionA particle shows distance-time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point

View SolutionWhich of the following decreases in motion along a straight line with constant retardation while the body is moving away from the origin?
View SolutionA bullet fired into a wooden block loses half of its velocity after penetrating 60cm. It comes to rest after penetrating a further distance of
View SolutionIt is given that `t= px^(2) + qx`, where x is displacement and t is time. The acceleration of particle at origin is
View SolutionA particle is moving with uniform acceleration along a straight line. The average velocity of the particle from P to Q is `8ms^(-1)` and that Q to S is `12ms^(-1)`. If QS= PQ, then the average velocity from P to S is

View SolutionThe velocity of a particle at an instant is 10m/s. After 5sec, the velocity of the particle is 20m/s. Find the velocity at 3 seconds before from the instant when velocity of a particle is 10m/s.
View SolutionA particle experiences a constant acceleration for 20 sec after starting from rest. If it travels distance `S_1` in the first 10 sec and a distance `S_2` in the next 10 sec, Then
View SolutionA body starts from rest from the origin with an acceleration of `6m//s^(2)` along x axis and `8m//s^(2)` along y axis.The distance from origin after 4 seconds will be
View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration `(4)/(3) ms^-2`, in the third second is.
View SolutionThe displacement x of a particle along a straight line at time t is given by : `x = a_(0) + (a_(1) t)/(2) + (a_(2))/(3) t^(2)`. The acceleration of the particle is
View SolutionAn automobile travelling with a speed `60 km//h` , can brake to stop within a distance of `20 m` . If the car is going twice as fast i. e. , `120 km//h`, the stopping distance will be
View SolutionA body travels 2m in the first two second and 2.20m in the next 4 second with uniform deceleration. The velocity of the body at the end of 9 second is
View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View SolutionA bus starts moving with acceleration `2 ms^-2`. A cyclist `96 m` behind the bus starts simultaneously towards the bus at a constant speed of `20 m//s`. After what time will he be able to overtake the bus ?
View Solutionmetro train starts from rest and in five seconds achieves a speed 108 km/h. After that it moves with constant velocity and comes to rest after travelling 45m with uniform retardation. If total distance travelled is 395 m, find total time of travelling.
View SolutionA particle starting with certain initial velocity and uniform acceleration covers a distance of 12m in first 3 seconds and a distance of 30m in next 3 seconds. The initital velocity of the particle is
View SolutionA particle travels 10m in first 5 sec and 10 m in next 3 sec. Assuming constant acceleration what is the distance travelled in next 2 sec.
View SolutionAn NCC parade is going at a uniform speed of 6 km/h thorugh a place under a berry tree on which a bird is sitting at a height of 12.1 m. At a particular instant the bird drops a berry. Which cadet (gie the distance from the tree at tehinstant) will receive the berry on his uniform?
View SolutionA particle starts from rest and travel a distance x with uniform acceleration, then moves uniformly a distance 2x and finally comes to rest after moving further 5x with uniform retardation. The ratio of maximum speed to average speed is
View SolutionA particle is moving in a straight line with initial velocity `u` and uniform acceleration `f`. If the sum of the distances travelled in `t^(th) and (t + 1)^(th)` seconds is `100 cm`, then its velocity after `t` seconds, in `cm//s`, is.
View SolutionA car is moving along a straight road with a uniform acceleration. It passes through two points P and Q separated by a distance with velocity `30km//h` and `40 km//h` respectively. The velocity of the car midway between P and Q is
View SolutionA particle starts moving rectilinearly at time `t=0` such that its velocity `v` changes with time `t` according to the equation `v=t^(2)-t`, where `t` is in seconds and `v` in `ms^(-1)`. Find the time interval for which the particle retards.
View SolutionA car , moving with a speed of `50 km//hr` , can be stopped by brakes after at least ` 6m `. If the same car is moving at a speed of `100 km//hr`, the minimum stopping distance is
View SolutionA particle moves along a staight line such that its displacement at any time t is given by `s=t^3-6t^2+3t+4m`. Find the velocity when the acceleration is 0.
View SolutionA particle moves along a straight line `OX`. At a time `t` (in seconds) the distance `x` (in metre) of the particle is given by `x = 40 +12 t - t^3`. How long would the particle travel before coming to rest ?
View SolutionA body is thrown upward and reaches its maximum height. At that position-
View SolutionA man throws balls with the same speed vertically upwards one after the other at an interval of 2s. What should be the speed of the throw so that more than two balls are in the sky at any time ? (Given `g = 9.8 m//s^(2)`)
View SolutionTwo bodies of different masses `m_(a)` and `m_(b)` are dropped from two different heights a and b. The ratio of the time taken by the two to cover these distances are
View SolutionA ball is dropped it on a floor and bounces back to a height somewhat less then the original height. The curve which its motion correctly about y and t is
View SolutionA stone is dropped from a rising balloon at a height of 76 m above the ground and reaches the ground in 6s. What was the velocity of the balloon when the stone was dropped?
View SolutionA boy standing at the top of a tower of 20m of height drops a stone. Assuming `g=10ms^(-2)`, the velocity with which it hits the ground is :-
View SolutionFind the ratio of the distance moved by a free-falling body from rest in fourth and fifth seconds of its journey.
View SolutionA ball dropped from a point A falls down vertically to C, through the midpoint B. The descending time from A to B and that from A to C are in the ratio
View SolutionA body dropped from top of a tower falls through ` 40 m` during the last two seconds of its fall. The height of tower in m is ( g= 10 m//s^@)`
View SolutionA ball is dropped downwards. After 1 second another ball is dropped downwards from the same point. What is the distance between them after 3 seconds
View SolutionA stone thrown vertically upwards with a speed of 5 m/sec attains a height `H_(1)`. Another stone thrown upwards from the same point with a speed of 10m/sec attains a height `H_(2)`. The correct relation between `H_(1) and H_(2)` is
View SolutionA ball is thrown vertically upwards with a speed of `10 m//s` from the top of a tower 200 m height and another is thrown vertically downwards with the same speed simultaneously. The time difference between them on reaching the ground is `(g=10 m//s^(2))`
View SolutionTwo stones are thrown from the top of a tower, one straight down with an initial speed u and the second straight up with the same speed u. When the two stones hit the ground they will have speeds in the ratio.
View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. `(g = 10 ms^-2)`
View SolutionA stone is dropped from the top of a tower 200 m high. At the same time, another stone is projected vertically upwards from the ground with a velocity of `40m//s`. Calcuate when and where the two stones will mest.
View SolutionA stone falls freely from rest from aheight `h` and it travels a distance `9h//25` in the last second. The value of `h` is
View SolutionA body A is thrown vertically upwards with initial velocity `v_(1)`. Another body B is dropped from a height h. Find how the distance x between the bodies depends on the time t if the bodies begin to move simultaneously.
View SolutionA juggler keeps on moving four balls in the air throwing the balls after regular intervals. When one ball leaves his hand `("speed" = 20 ms^-1)` the positions of other balls (height in m) `("Take" g = 10 ms^-2)`.
View SolutionSimilar balls are thrown vertically each with a velocity `20ms^(-1)`, one on the surface of earth and the other on the surface of moon. What will be ratio of the maximum heights attained by them? (Acceleration on moon `= 1.7 ms^(-2)` approx)
View SolutionTwo trains are each 50 m long moving parallel towards each other at speeds `10 ms^(-1)` and `15 ms^(-1)` respectively, at what time will they pass each other ?
View SolutionA train of `150 m` length is going toward north direction at a speed of `10 ms^-1`. A parrot flies at a speed of `5 ms^-1` toward south direction parallel to the railway track. The time taken by the parrot to cross the train is equal to.
View SolutionAn object has velocity `vecv_1` w.r.t. ground. An observer moving with constant velocity `vecv_0` w.r.t. ground measures the velocity of the object as `vecv_2`. The magnitudes of three velocities are related by
View SolutionA boat takes two hours to travel 8 km and back in still water. If the velocity of water is 4 km/h, the time taken for going upstream 8 km and coming back is
View SolutionWhich one of the following represents displacement-time graph of two objects A and B moving with zero relative velocity?
View SolutionA car is standing 800 m behind a bus, which is also at rest. The two start moving at the same instant but the different forward accelerations. The bus has acceleration `4m//s^(2)` and the car has acceleration `8m//s^(2)`. The car will catch up with the bus after a time of:
View SolutionA thief running away on a straight road on a jeep moving with a speed of 9m/s. A police man chases him on a motor cycle moving at a speed of 10m/s. If the instantaneous separation of jeep from the motor cycle is 100m, how long will it take for the policemen to catch the thief?
View SolutionThree particles `A,B` and `C` and situated at the vertices of an equilateral triangle `ABC` of side of length `l` at time `t=0`,Each of the particles move with constant speed `u`. A always has its velocity along `AB, B` along `BC` and `C` along `CA`.
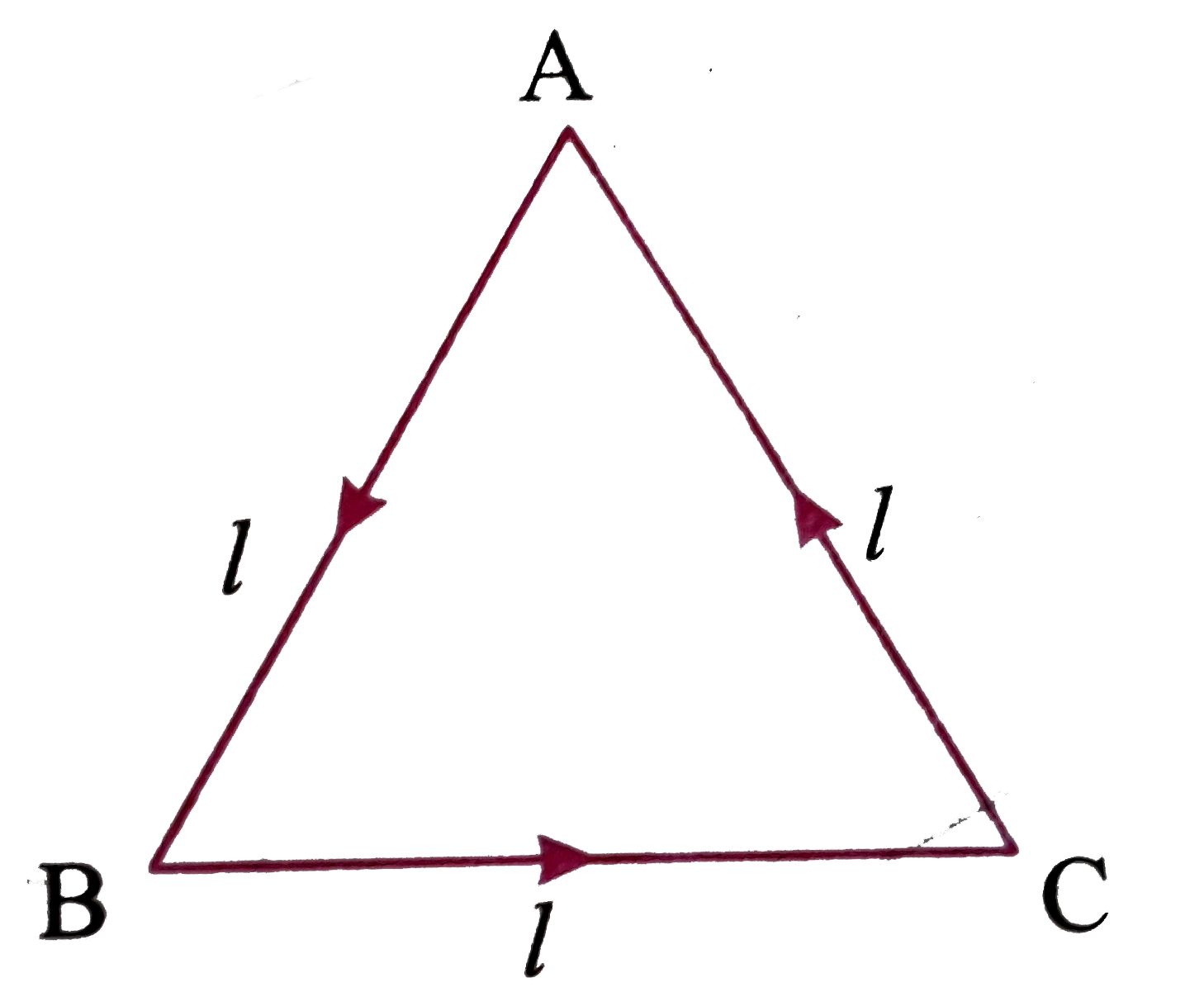
View SolutionA ball is thrown vertically upward with a velocity u from balloon descending with a constant velocity v. The vall will pass by the balloon after time
View SolutionA bus is moving with a speed of `10 m s^(-1)` on a straight road. A scooterist wishes to overtake the bus in 100 s. If the bus is at a distance of 1 km from the scooteritst with what speed should the scooterist chase the bus?
View SolutionA man running on the horizontal road at ` 8 km h^(-1)` find the rain appears to be falling vertically. He incresases his speed to `12 km h^(-1)` and find that the drops make angle ` 30^2` with the vertical. Fin dthe speed and direction of the rain with respedt to the road.
View SolutionAn airplane flies from a town A to a town B when there is no wind and takes a total time `T_(0)` for a return trip. When there is a wind blowing in a direction from town A to town B, the plane's time for a similar return trip, `T_(w)`, would satisfy
View Solution
Exercise-1 questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of DISHA PUBLICATION PHYSICS (HINGLISH) of Class 12