Complete Solutions to Exercise -2 : CONCEPT APPLICATOR of chapter MOTION IN A PLANE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| DISHA PUBLICATION | Exercise -2 : CONCEPT APPLICATOR |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
The value of a for which the points A,B,C with position vectors `2hati-hatj+hatk, hati-3hatj-5hatk and ahati-3hatj+hatk` respectively are the vertices are the vetices of a righat angled triangle with `C=pi/2` are (A) `-2 and -1` (B) `-2 and 1` (C) `2 and -1` (D) `2 and 1
View SolutionTwo particles start simultaneously from the same point and move along two straight lines. One with uniform velocity v and other with a uniform acceleration a. if `alpha ` is the angle between the lines of motion of two particles then the least value of relative velocity will be at time given by
View SolutionA projectile A is thrown at an angle of `30^@` to the horizontal from point P. At the same time, another projectile B is thrown with velocity `v_2` upwards from the point Q vertically below the highest point. For B to collide with A, `v_2/v_1` should be

View SolutionLet `vecu, vecv and vecw` be such that `|vecu|=1,|vecv|=2 and |vecw|=3` if the projection of `vecv " along "h vecu` is equal to that of `vecw` along `vecu` and vectors `vecv and vecw` are perpendicular to each other then `|vecu-vecv + vecw|` equals
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle `theta` to the vertical. The velocity of rain with respect to the ground is :
View SolutionFrom a point on the ground at a distance of 2m from the fot of a verticle wal, a ball is thrown at an angle of `45^(@)` which just clears the top of the wall and then strikes the ground at distance of 4m from the foot of the wall on the other side. The height of the wall is
View SolutionA particle is projected over a traingle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If `alpha` and `beta` be the base angles and `theta` the angle of projection, prove that `tan theta = tan alpha + tan beta`.
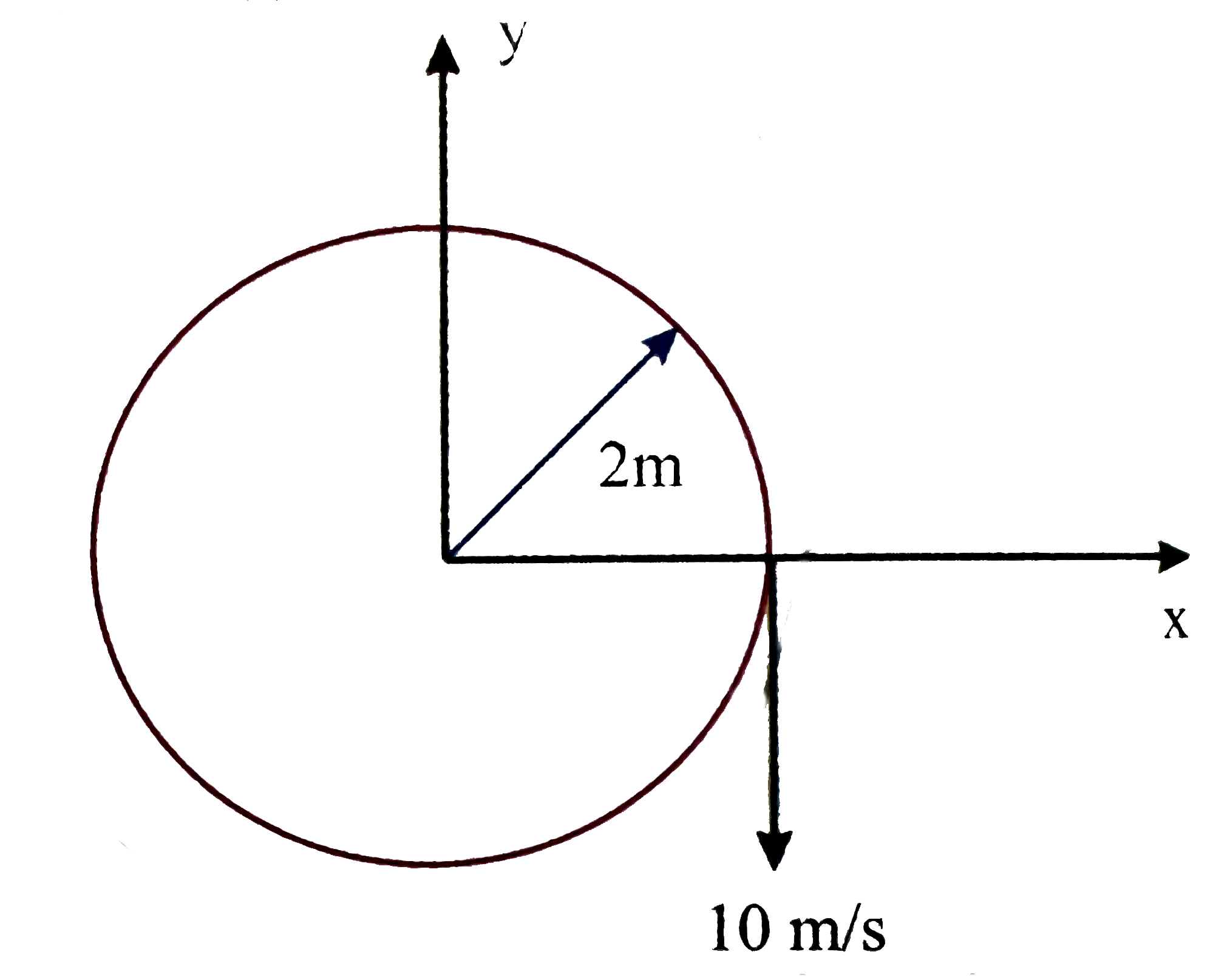
View SolutionA particle is moving along a circular path in `xy`-plane.When its crosses `x`-axis,it has an acceleration along the path of `1.5m//s^(2)`, and is moving with a speed of `10 m//s` in `-ve` `y`-direction.The total acceleration is
View SolutionAn aircraft moving with a speed of 250 m/s is at a height of 6000 m, just overhead of an anti aircraft gun. If the muzzle velocity is 500 m/s, the firing angle `theta` should be:

View SolutionA cricket ball thrown across a field is at heights `h_(1)` and `h_(2)` from the point of projection at time `t_(1)` and `t_(2)` respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
View SolutionIf the equation for the displacement of a particle moving in a circular path is given by `(theta)=2t^(3)+0.5`, where `theta` is in radians and `t` in seconds, then the angular velocity of particle after `2 s` from its start is
View SolutionLet `veca,vecb and vecc` be the non zero vectors such that `(vecaxxvecb)xxvecc=1/3 |vecb||vecc|veca.` if theta is the acute angle between the vectors `vecb and veca` then theta equals (A) `1/3` (B) `sqrt(2)/3` (C) `2/3` (D) `2sqrt(2)/3`
View SolutionTwo balls are projected simultaneously in the same vertical plane from the same point with velocities `v_1` and `v_2` with angle `theta_1` and `theta_2` respectively with the horizontal. If `v_1` cos `theta_1 =v_2 cos theta_2`, the path of one ball as seen from the position of other ball is :
View SolutionConsider a collection of a large number of particles each with speed `v` in a plane.The direction of velocity is randomly distributed in the collection.The magnitude of the average relative velocity of a particle with velocities of all other particles is
View SolutionA cannon on a level plane is aimed at an angle `theta` above the horizontal and a shell is fired with a muzzle velocity `v_(0)` towards a vertical cliff a distance D away. Then the height from the bottom at which the shell strikes the side walls of the cliff is
View SolutionA wheel is subjected to uniform angular acceleration about its axis. Initially, its angular velocity is zero. In the first `2 sec`, it rotates through an angle `theta_(1)`, in the next `2 sec`, it rotates through an angle `theta_(2)`. The ratio of `theta_(2)//theta_(1)` is
View SolutionA ball is thrown from a point with a speed 'v^(0)' at an elevation angle of `theta` . From the same point and at the same instant , a person starts running with a constant speed `('v_(0)')/(2) ` to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection `theta` ?
View SolutionA boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle ` 30 ^@ ` with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground?
` (g = 10 m//s ^ 2 ) `
View SolutionIf the vector `vecx` satisfying `vecx xx veca +(vecx .vecb) vecc=vecd` be given by `vecx=lambda veca+veca xx (veca xx (vecd xx vecc))/((veca.vecc)veca^2)` , then `theta` is equal to
View SolutionA projectile moves from the ground such that its horizontal displacement is `x=Kt` and vertical displacement is `y=Kt(1-alphat)`, where K and `alpha` are constants and t is time. Find out total time of flight (T) and maximum height attained `(Y_"max")`
View SolutionA particle is projected horizontally with a speed `u` from the top of plane inclined at an angle `theta` with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA man can swim in still water with a speed of `2 ms^-1`. If he wants to cross a river of water current speed `sqrt(3) ms^-1` along the shortest possible path, then in which direction should he swim ?
View SolutionWhich of the following plots correctly represents the variation of the magnitude of acceleration `|a_R|` with time t for a particle projected at t=0 with speed `v_0` at an angle `theta` above the horizontal?
View SolutionA point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P' is such that it sweeps out a length `s=t^3+5`, where s is in metres and t is in seconds. The radius of the path is 20 m. The acceleration of 'P' when t =2 s is nearly.

View SolutionA particle of unit mass is projected with velocity u at an inclination `alpha` above the horizon in a medium whose resistance is k times the velocity. Its direction will again make an angle `alpha` with the horizon after a time
View SolutionThe maximum range of a bullet fired from a toy pistol mounted on a car at rest is `R_(0)=40m`. What will be the acute angle of inclination of the pistol for maximum range when the car is moving in the direction of firing with uniform velocity `V=20m//s`, on a horizontal surface? `(g=10m//s^(2))`
View SolutionA stone must be projected horizontally from a point P, which is h metre above the foot of a plane inclined at an angle `theta` with horizontal as shown in figure. What is the velocity v of the stone so that it may hit the inclined plane perpendicularly?

View SolutionTwo boats, A and B, move away from a buoy anchored at the middle of a river along the mutually perpendicular straight lines: the boat A along the river, and the boat B across the river. Having moved off an equal distance from the buoy the boats returned. Find the ratio of times of motion of boats `tau_A//tau_B` if the velocity of each boat with respect to water is `eta=1.2` times greater than the stream velocity.
View Solution
Exercise -2 : CONCEPT APPLICATOR questions and complete solutions for chapter MOTION IN A PLANE of DISHA PUBLICATION PHYSICS (HINGLISH) of Class 12