Complete Solutions to EXERCISE-2 : CONCEPT APPLICATOR of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| DISHA PUBLICATION | EXERCISE-2 : CONCEPT APPLICATOR |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
Light of wavelength `6.5xx10^(-7)`m is made incident on two slits 1 mm apart. The distance between third dark fringe and fifth bright fringe on a screen distant 1 m from the slits will be
View SolutionIn a two slit experiment with monochromatic light fringes are obtained on a screen placed at some distance from the sits. If the screen is moved by `5xx10^-2m` towards the slits the change in fringe width is `3xx10^-5m`. If separation between the slits is `10^-3m`, the wavelength of light used
View SolutionIn Young's experiment the distance between two slits is `d/3` and the distance between the screen and the slits is 3D. The number of fringes in `1/3` metre on the screen, formed by monochromatic light of wavelength `3lambda`, will be:
View SolutionIn a Young's double slit experiment, if the incident light consists of two wavelengths `lamda_(1)andlamda_(2)`, the slit separation is d, and the distance between the slit and the screen is D, the maxima due to the two wavelengths will coincide at a distance from the central maxima, given by :
View SolutionTwo ideal slits `S_(1)` and `S_(2)` are at a distance `d` apart, and illuninated by light of wavelength `lambda` passing through an ideal source slit `S` placed on the line through `S_(2)` as shown. The distance between the planes of slits and the source slit is `D.A` screen is held at a distance `D` from the plane of the slits. The minimum value of `d` for which there is darkness at `O` is `(dlt lt D)`
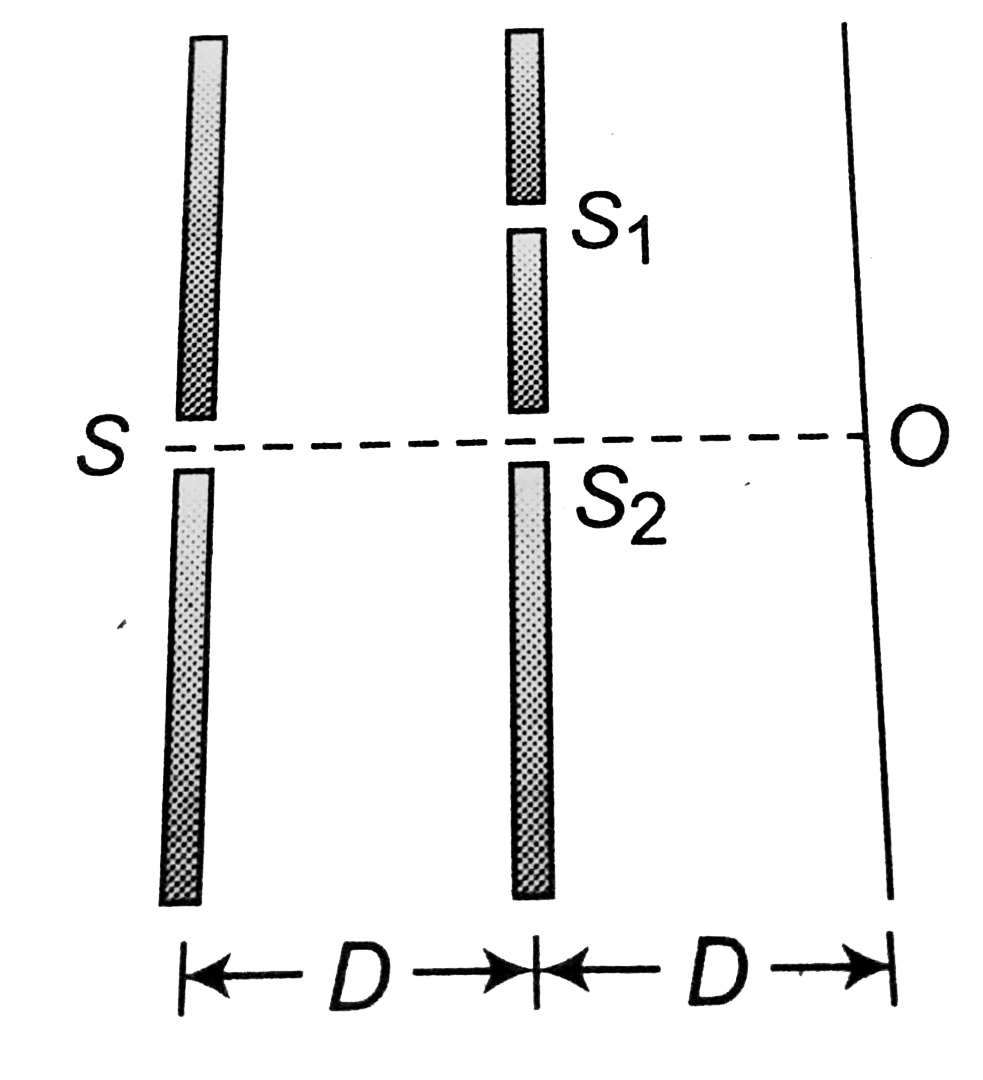
View SolutionA micture of light, consisting of wavelength 590nm and an unknown wavelength, illuminates Young's double slit and gives rise to two overlapping interference patterns on the scree. The central maximum of both lights coincide. Further, it is obseved that the third bright fringe of known light coincides with the 4th bright fringe of the unknown light. From this data, the wavelength of the unknown light is:
View SolutionThe central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of 4th dark fringe after a glass sheet of refractive index 1.5 is introduced. The thickness of glass sheet would be
View SolutionFigure shows two light rays that are initially exactly in phase and that reflect from several glass surfaces. Neglect the slight slant in the path of the light in the second arrangement. The path length difference in terms of wavelength `lamda` is :
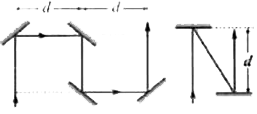
View SolutionIn young's double slit experiment the slits are illumated by light of wavelength `5890^(@)` A and the distance between the fringes obtained on the screen is `0.2^(@)`. If the whole apparatus is immersed in water then the angular fringe width will be, if the refractive index of water is `4//3`
View SolutionIn a double slit experiment, the two slits are 1 mm apart and the screen is placed 1 m away. A monochromatic light of wavelength 500 mm is used.what will be the width of each slit for obtaining ten maxima of double slit within the central maxima of single slit pattern?
View SolutionIn a Young's double slit experiment, the two slits act as coherent sources of waves of equal amplitude A and wavelength `lamda` in another experiment with the same arrangement the two slits are made to act as incoherent sources of waves of same amplitude and wavelength. if the intensity at the middle point of the screen in te first case is `I_(1)` and in te second case `I_(2)` then the ratio `(I_(1))/(I_(2))` is
View SolutionIn Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is `(3//2)x`. The refractive index of the second plate is
View SolutionThere are two plane mirrors. They are mutually inclined as shown in figure. S is a source of monochromatic light of wavelength `lamda`. The reflected beam interfere and fringe pattern is obtained on the screen. If `theta` is small, the fringe width will be :
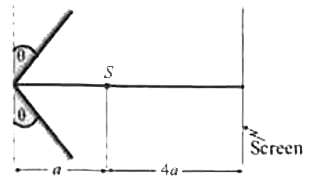
View SolutionIn the ideal double-slit experiment, when a glass-plate(refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wave-length `lamda`), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
View SolutionA thin glass plate of thickness is `(2500)/3lamda` (`lamda` is wavelength of light used) and refractive index `mu=1.5` is inserted between one of the slits and the screen in Young's double slit experiment. At a point on the screen equidistant from the slits, the ratio of the intensities before and after the introduction of the glass plate is :
View SolutionIn Young's double slit experiment, wavelength `lambda=5000Å` the distance between, the slits is `0.2mm` and the screen is at 200cm from the slits. The central maximum is at `x=0` The third maximum (Taking the central maximum as zeroth maximum) will be at x equal to
View SolutionA person lives in a high-rise building on the bank of a river 50 m wide. Across the river is a well it tower of height 40 m. When the person, who is at a height of 10 m, looks through a polarizer at an appropriate angle at light of the tower reflecting from the river surface, he notes that intensity of light coming from distance X from his building is the least and this corresponds to the light coming from light bulbs at height 'Y' on the tower. The values of X and Y are respectively close to (refractive index of water = `4/3`)

View SolutionA broad sources of light of wavelength `680nm` illuminated normally two glass plates.`120nm`long that meet at one end and are separated by a wire`0.048 mm`in diameter at the other end,Find the number of bright fringes formed over the `120nm`distance.

View SolutionA thin film of soap solution `(mu_(s)=1.4)` lies on the top of a glass plate `(mu_(g)=1.5)`. When visible light is incident almost normal to the plate, two adjacent reflection maxima are observed at two wavelengths 420 and 630 nm. The minimum thickness of the soap solution is
View SolutionIn Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
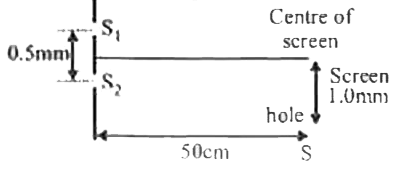
View SolutionIn a Young's double slit experiment, the separation between the two slits is d and the wavelength of the light is `lamda`. The intensity of light falling on slit 1 is four times the intensity of light falling on slit 2. Choose the correct choice (s).
View SolutionA beam of light consisting of two wavelength `6500Å&5200Å`is used to obtain interferance fringes in a young's double slit experiment .The distance between the slits is `2.0mm` and the distance between the plane of the slits and thescreen is `120cm`,.what is the least distance from the central maximum where the bright fringes due to both the wave length coincides?
View SolutionFig, here shows P and Q as two equally intense coherent sources emitting radiations of wavelength 20m. The separation PQ si 5m, and phase of P is ahead of the phase Q by `90^(@)`. A, B and C are three distant points of observation equidistant from the mid - point of PQ. The intensity of radiations of A, B, C will be in the ratio

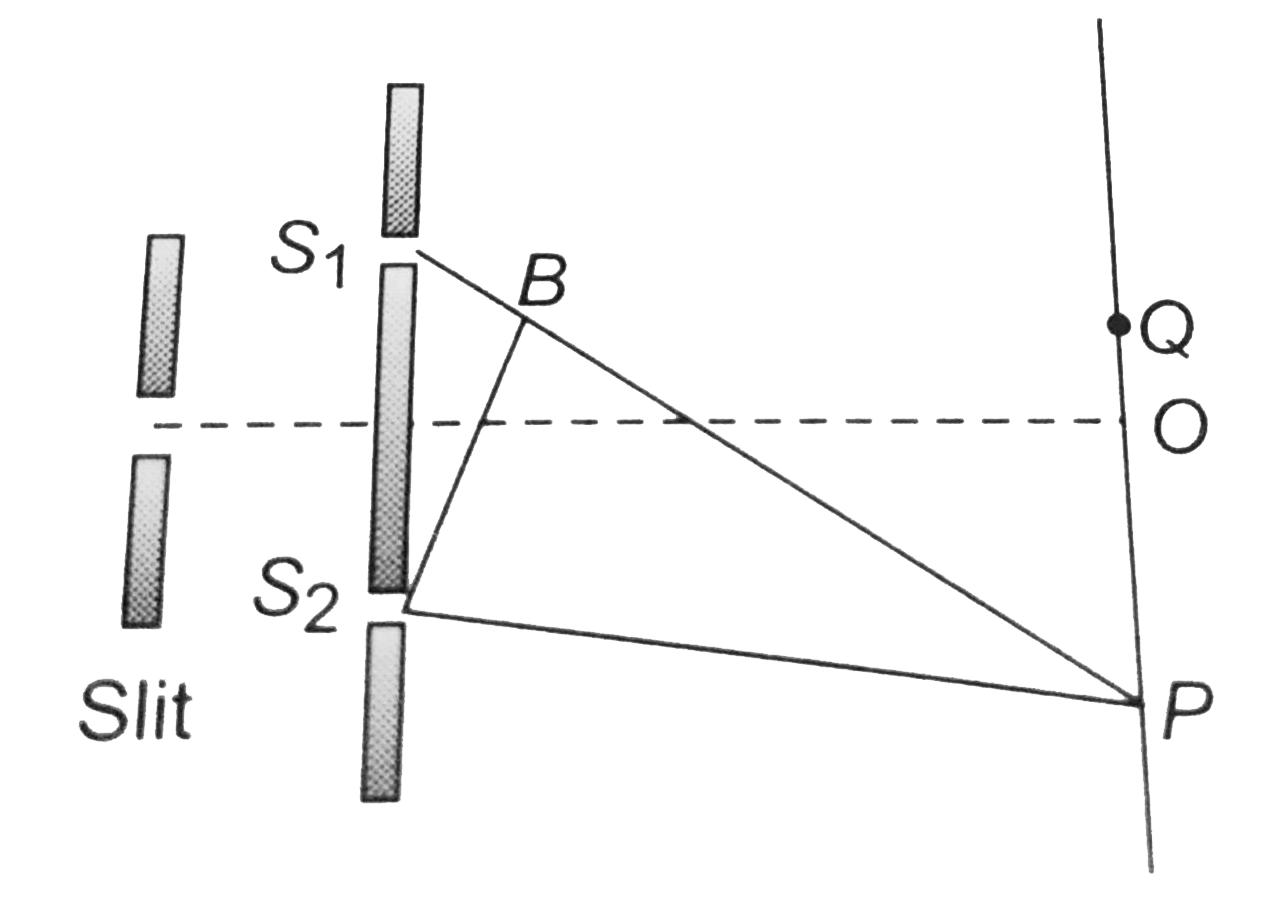
View SolutionIn the figure is shown Young's double slit experiment. Q is the position of the first bright fringe on the right side of O. P is the `11^(th)` bright fringe on the other side, as measured from Q. If the wavelength of the light used is `600 nm`. Then `S_(1)B` will be equal to
View SolutionIn Young's double slit experiment, we get 10 fringes in the field of view of monochromatic light of wavelength 4000Å. If we use monochromatic light of wavelength 5000Å, then the number of fringes obtained in the same field of view is
View SolutionLight of wavelength `6328Å` is incident normally on slit having a width of `0.2mm`The width of the central maximum measured form minimum to minimum of diffraction pattens on a screen `9.0meter`away will be about-
View SolutionIn Young's double slit experiment, the distnace between two sources is `0.1//pimm`. The distance of the screen from the source is 25 cm. Wavelength of light used is `5000Å` Then what is the angular position of the first dark fringe.?
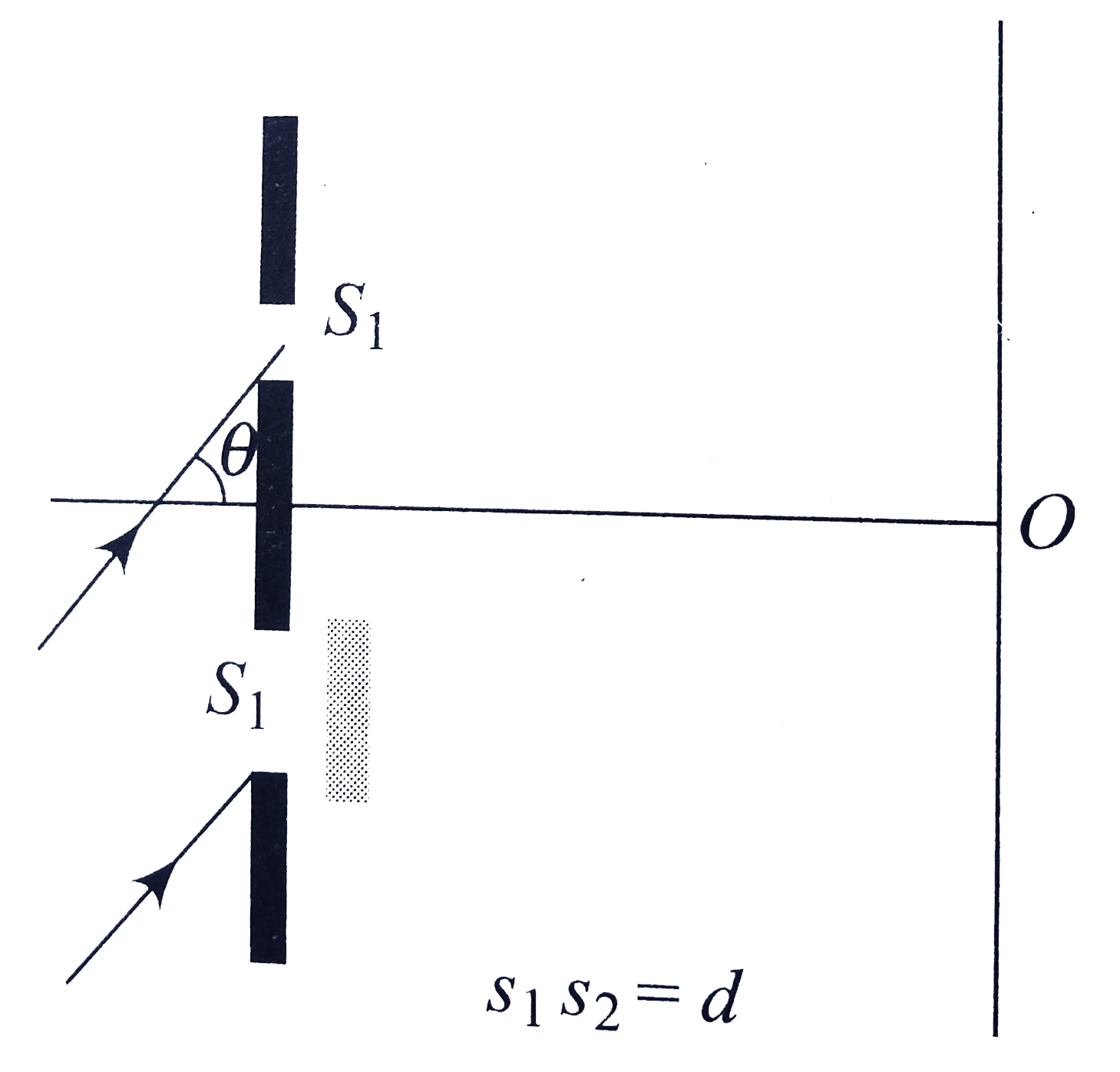
View SolutionA monochromatic beam of light fall on YDSE apparatus at some angle (say `theta`) as shown in figure. A thin sheet of glass is inserted in front of the lower slit `s_(2)`. The central bright fringe (path difference `= 0`) will be obtained
View SolutionAn equiconvex lens of focal length 10 cm (in air) and R.I. 3/2 is put at a small opening on a tube of length 1 m fully filled with liquid of R.I. 4/3. A concave mirror of radius of curvature 20 cm is cut into two halves `M_(1)andM_(2)` and placed at the end of the tube. `M_(1)andM_(2)` are placed such that their principal axes AB and CD respectively are separated by 1 mm each from the principal axis of the lens. A slit S placed in air illuminates the lens with light of frequency `7.5xx10^(14)Hz`. The light reflected from `M_(1)andM_(2)` forms interference pattern on the left end EF of the tube. O is an opaque substance to cover the hole left by `M_(1)andM_(2)`. Width of the fringes on EF is `(x xx10)mum`. Find the value of x.

View SolutionIn YDSE, having slits of equal width, let `beta` be the fringe width and `I_(0)` be the maximum intensity. At a distance x from the central brigth fringe, the intensity will be
View Solution
EXERCISE-2 : CONCEPT APPLICATOR questions and complete solutions for chapter WAVE OPTICS of DISHA PUBLICATION PHYSICS (HINGLISH) of Class 12