Complete Solutions to Critical Thinking(Objective Questions) of chapter मात्रक, विमायें तथा मापन of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | मात्रक, विमायें तथा मापन |
| ERRORLESS HINDI | Critical Thinking(Objective Questions) |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
यदि गुरुत्वीय त्वरण `10` मी `//`से `""^(2)` है तथा यदि लंबाई व समय के मात्रक बदलकर क्रमशः किमी तथा घण्टा कर दिये जाएँ तो त्वरण का नया संख्यात्मक मान होगा
View Solutionयदि L,C तथा R क्रमशः प्रेरकत्व , धारिता तथा प्रतिरोध प्रदर्शित करते हैं , तो निम्न में से कौन आवृत्ति की विमायें प्रदर्शित नहीं करेगा
View Solutionएक पेंचमापी के वृतीय स्केल पर 50 खण्ड है, और पिच की लम्बाई 0.5mm है गोले का व्यास ज्ञात कीजिये मुख्य स्केल का मापन 2 है |
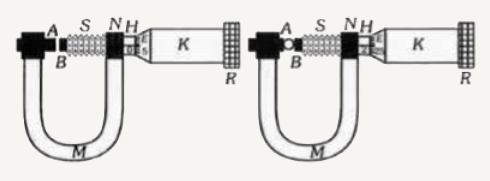
View Solutionसामान्य प्रतीकों के अनुसार समीकरण `S_(t) = u+ (1)/(2)a(2t-1)`
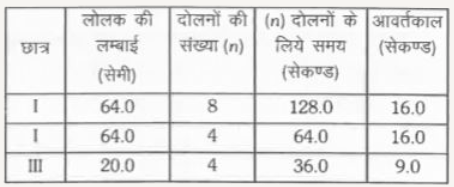
View Solutionसरल लोलक की सहायता से छात्र I , II तथा III गुरूत्वीय त्वरण मापन के लिये एक प्रयोग करते हैं | वे सरल लोलक की भिन्न लम्बाई प्रयुक्त करते हैं और / अथवा विभिन्न दोलन संख्या के लिये समय नोट करते हैं | सारिणी में प्रेक्षण दर्शाये गये हैं |
लम्बाई के लिये अल्पतमांक = 0.1 सेमी
समय के लिये अल्पतमांक = 0.1 सेकण्ड
छात्र I , II तथा III के लिये g में प्रतिशत त्रुटि अर्थात `((Deltag)/(g)xx100)` क्रमशः `E_(I), E_(II)` तथा `E_(III)` है, तब
View Solutionएक दृढ़ घन A का द्रव्यमान M एवं इसकी प्रत्येक भुजा की लम्बाई L है, यह एकसमान विमा के , दूसरे कम दृढ़ता गुणांक `(eta)` वाले घन B के ऊपर इस प्रकार से स्थित है कि A का निचला पृष्ठ B के ऊपरी पृष्ठ को पूरी तरह ढक लेता है | B की निचली सतह दृढ़ता से क्षैतिज सतह पर स्थित है | एक अल्प परिमाण का बल F, A की एक सतह पर लम्बवत् लगाया जाता है | बल को हटाने पर A छोटे दोलन करने लगता है जिसका आवर्तकाल दिया जाता है |
View Solutionमाध्यम में संचरित तरंग के प्रभाव में समय t पर, स्थिति x पर स्थित एक कण का विस्थापन समीकरण y = asin ( bt - cx ) है , जहाँ a , b तथा c तरंग के नियतांक हैं | निम्न में से कौनसी राशि की विमा है
View Solutionएक तार का द्रव्यमान `0.3 +- 0.003g` , त्रिज्या `0.5+- 0.005mm` तथा लम्बाई `6 +- 0.06 cm` है | इसके घनत्व के मापन में अधिकतम प्रतिशत त्रुटि होगी
View Solutionवास्तविक गैसों के लिये वाण्डर वाल अवस्था समीकरण `(P+(a)/(V^(2)))(V-b)=nRT` है | निम्नलिखित में से किसकी विमा, ऊर्जा से भिन्न है
View Solutionसूत्र `X = 3YZ^(2)` में X और Z क्रमशः धारिता और चुम्बकीय क्षेत्र की विमायें हैं | MRSA पद्धति में Y की विमायें हैं
View Solutionव्यंजक `P=(alpha)/(beta)e^((alphaz)/(ktheta))` में P दाब , Z दूरी , k बोल्ट्जमैन स्थिरांक एवं `theta` तापक्रम दर्शाता है तो `beta` का विमीय सूत्र होगा
View Solutionतार के कम्पन की आवृत्ति `v=(p)/(2l)[(F)/(m)]^(1//2)` से दी जाती है | यहाँ p तार के लूपों की संख्या एवं l लम्बाई है | m का विमीय सूत्र होगा
View SolutionSI मात्रकों में एक पदार्थ का घनत्व `128kgm^(-3)` है | एक ऐसे मात्रकों में , जिसमें लम्बाई की इकाई 25 cm तथा द्रव्यमान की इकाई 50g है , इस पदार्थ के घनत्व का आंकिक मान होगा
View Solutionएक पेचमापी की पिच तथा वृत्तीय पैमाने पर भागों की संख्या क्रमशः 0.5 mm तथा 100 है | जब पेचमापी को बिना किसी वस्तु के पूरी तरह कस दिया जाता है , तो इसके वृत्तीय पैमाने का शून्य मध्य रेखा से तीन भाग नीचे आता है | एक पतली चादर की मोटाई के लिए इस पेचमापी के मुख्य पैमाने तथा वृत्तीय पैमाने का पाठ्यांक , क्रमशः 5.5mm तथा 48 हैं | तो चादर की मोटाई होगी
View SolutionG ( सार्वत्रिक गुरुत्वाकर्षण नियतांक ) , h ( प्लांक नियतांक ) तथा c ( प्रकाश की गति )के रूप में समय का समतुल्य संबंध निम्न में किसके समानुपाती होगा
View Solutionएक मीटर स्केल द्वारा नापने पर किसी बेलन का व्यास और ऊँचाई क्रमशः `12.6 +- 0.1cm` और `34.2 +- 0.1cm` आते है | उपयुक्त सार्थक अंकों में इसके आयतन का मान क्या होगा
View Solutionयदि गति ( V ) त्वरण ( A ) तथा बल ( F ) को मूल भौतिक इकाइयाँ मानें तो , यंग प्रत्यास्थता गुणांक की विमा होगी
View Solutionएक पेंचमापी के मुख्य पैमाने का अल्पतमांक 1mm है | `10mum` व्यास के तार का व्यास नापने के लिए इसके वृत्तीय पैमाने पर न्यूनतम भागों की संख्या होगी
View SolutionSI इकाई में `sqrt((in_(0))/(mu_(0)))` की विमा है
View Solutionयदि पृष्ठ तनाव ( S ) , जड़त्व आघूर्ण ( 1 ) तथा प्लांक नियतांक ( h ) को मूलभूत इकाई मानें तो रेखीय संवेग का विमा सूत्र होगा
View Solutionएक घनाकार गुटके का घनत्व निकालने के लिए , उसका द्रव्यमान कोर की लम्बाई, क्रमशः `( 5.00 +- 0.10 ) kg" तथा "( 0.1 +- 0.01 ) m` मापी जाती है | घनत्व के मापन की त्रुटि होगी
View Solutionएक वर्ग का क्षेत्रफल `5.29cm^(2)` है | ऐसे सात वर्गों का क्षेत्रफल उचित सार्थक अंकों में होगा
View Solutionसूत्र `X = 5YZ^(2)` में X तथा Z की विमायें , क्रमशः धारिता तथा चुम्बकीय क्षेत्र हैं | SI इकाई में Y की विमा क्या होगी
View Solutionनिम्नांकित में से किस संयोजन की विमा वही है , जो, विद्युत प्रतिरोध की है ( यहाँ, `epsilon_(0)`, निर्वात की विद्युतशीलता ( परावैद्युतांक ) तथा `mu_(0)` निर्वात की चुम्बकशीलता है
View Solutionएक सरल दोलक के प्रयोग , जिसमें गुरूत्वीय त्वरण ( g ) मापना है , में 20 दोलनों का समय एक 1 sec अल्पतमांक वाली एक विराम घड़ी से मापते हैं | इस समय का माध्य मान 30s आता है | दोलक की लम्बाई को 1 mm अल्पतमांक के पैमाने से मापने पर 55.0 cm आती है | g के मापन में प्रतिशत त्रुटि का सन्निकट मान होगा
View Solutionकिसी प्रयोग में भौतिक राशियों A, B , C और D की माप में होने वाली त्रुटि की प्रतिशतता क्रमशः `1 % , 2 % , 3 %` और `4 %` है | तब X की माप , जबकि `X=(A^(2)B^(1//2))/(C^(1//3)D^(3))` है , में अधिकतम प्रतिशत त्रुटि होगी
View Solution
Critical Thinking(Objective Questions) questions and complete solutions for chapter मात्रक, विमायें तथा मापन of ERRORLESS PHYSICS (HINDI) of Class 12