Complete Solutions to Ordinary Thinking (Objective Questions)(मापन में त्रुटियाँ) of chapter मात्रक, विमायें तथा मापन of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | मात्रक, विमायें तथा मापन |
| ERRORLESS HINDI | Ordinary Thinking (Objective Questions)(मापन में त्रुटियाँ) |
| Number Of Questions | 44 |
| Academic Year | 2023-24 |
सरल लोलक का दोलन काल `T = 2pisqrt((I)/(g))` से दिया जाता है , जहाँ I लगभग 100 cm है तथा न्यूनतम 1mm तक शुद्धता से मापा जाता है | दोलन काल ( T ) लगभग 2 सैकण्ड है | यदि 100 दोलनों के समय को उस घड़ी से मापा जाए जिसका अल्पतमांक 0.1 सैकण्ड है , तो g में प्रतिशत त्रुटि होगी
View Solutionद्रव्यमान तथा चाल के मापन से प्राप्त द्रव्यमान तथा चाल में प्रतिशत त्रुटियाँ क्रमशः `2%` तथा `3 %` हैं | गतिज ऊर्जा की गणना में अधिकतम त्रुटि होगी
View Solutionएक विराम घड़ी की सहायता से एक लोलक के दोलन का आवर्त काल 2.5 सेकण्ड मापा जाता है , `(1)/(2)` जिसमें सेकण्ड की त्रुटि है | तब मापन में प्रतिशत आंशिक त्रुटि होगी
View Solutionएक प्रयोग में एक उपकरण द्वारा कोण मापने की आवश्यकता होती है | इस उपकरण में मुख्य पैमाने के 29 भाग वर्नियर पैमाने के 30 भागों के यथातथ्य संपाती हैं | यदि मुख्य पैमाने का लघुत्तम भाग आधे अंश `( 0.5^(@))` के बराबर है , तब इस उपकरण का अल्पतमांक है
View Solutionकिसी स्क्रूगेज के वृत्तीय पैमाने के दो पूर्ण फेरों द्वारा इसके मुख्य पैमाने पर तय की गई दूरी 1 mm है | वृत्तीय पैमाने पर कुल भागों की संख्या 50 है | साथ ही यह पाया जाता है कि स्क्रूगेज में -0.03 mm की शून्यांक त्रुटि है | इस स्क्रूगेज द्वारा किसी पतले तार का व्यास मापते समय कोई विद्यार्थी मुख्य पैमाने का पाठ्यांक 3mm तथा वृत्तीय पैमाने के 35 वें भाग को मुख्य पैमाने की लाईन में पाता है | तब तार का व्यास है
View Solutionसैकण्ड लोलक का माध्य आवर्तकाल 2 सैकण्ड है तथा आवर्तकाल में माध्य निरपेक्ष त्रुटि 0.05 सैकण्ड है | अधिकतम संभावित त्रुटि के साथ आवर्तकाल को किस प्रकार लिखा जाना चाहिये
View Solutionएक विद्यार्थी ने एक छड़ की लम्बाई मापकर 3.50 cm लिखी | इसको मापने में उसे किस उपकरण का प्रयोग किया
View Solutionएक डायोड की धारा - वोल्टता सम्बन्ध `I = ( e^(100OV//T) -1 ) mA` से दी जाती हैं | जहाँ V लगाई गई वोल्टता वोल्ट में है और तापमान T डिग्री कैल्विन में है | यदि एक विद्यार्थी 300 K पर 5 mA धारा नापते हुये मापन में `+-0.01V` की त्रुटि करता है , तब धारा के मान में mA में त्रुटि क्या होगी
View Solutionप्रतिशत त्रुटि की इकाई है
View Solutionयदि किसी गोले की त्रिज्या के मापन में त्रुटि `2 %` है , तो गोले के आयतन मापन में त्रुटि होगी
View Solutionवर्नियर कैलीपर्स में , मुख्य स्केल का 1 खाना x cm है तथा वर्नियर स्केल के ने , मुख्य स्केल के ( n - 1 ) खानों से सम्पाती होते हैं | वर्नियर कैलीपर्स का अल्पतमांक ( सेमी में ) है
View Solutionएक छात्र `g =(4pi^(2)l)/(T^(2))` की गणना के लिए एक प्रयोग करता है | `l~~1mm` तथा वह `Deltal` त्रुटि देता है | इसके लिये वह `DeltaT` अल्पतमांक की विराम घड़ी से n दोलन का समय प्राप्त करता है तथा मानवीय त्रुटि 0.1s देता है | निम्न में किस आंकड़े के लिए g का मापन शुद्ध होगा
View Solutionl लम्बाई के ताँबे के पतले तार के ताप में `10^(@)C` की वृद्धि करने पर इसकी लम्बाई में `2 %` की वृद्धि हो जाती है | यदि ताँबे की वर्गाकार प्लेट ( जिसकी भुजा की लम्बाई l है ) के ताप में `10^(@)C` की वृद्धि कर दी जाए तो इसके क्षेत्रफल में होने वाली प्रतिशत वृद्धि होगी
View Solutionव्यंजक `2dsin theta= lambda` का उपयोग करते हुए हम `theta` को माप कर d का मान जानना चाहते हैं | `theta` का मान 0 व `90^(@)` के बीच में है | तरंगदैर्ध्य का मान हमें परिशुद्धतः ज्ञात है तथा `theta` के मापने में त्रुटि, `theta` के सभी मानों के लिए समान है | जैसे `theta` का मान `0^(@)` से बढ़ता है तब
View Solutionएक भौतिक प्राचल a का मान तथा `a=b^(alpha)c^(beta)//d^(gamma)e^(delta)` सम्बन्ध के प्रयोग से b,c,d तथा e प्राचलों को मापकर निर्धारित किया जाता है | यदि b , c, d तथा e में अधिकतम त्रुटियाँ क्रमशः `b_(1) % C_(1) % d_(1) % व e_(1) %` , हैं तो प्रयोग द्वारा a के मापन में अधिकतम त्रुटि होगी
View Solutionदो वर्नियर कैलिपर्स इस तरह से है कि उनके मुख्य पैमाने का 1 सेमी, 10 समभागो में विभाजित है। एक कैलिपर्स `(C_(1))` के वर्नियर पैमाने पर 10 बराबर भाग है जोकि मुख्य पैमाने के 9 भागो के बराबर है। दूसरे कैलिपर्स `(C_(2))` के वर्नियर पैमाने पर भी 10 बराबर भाग है जोकि पैमाने के 11 भागो के बराबर है। दोनों कैलिपर्स के पठनो को चित्र में दर्शाया गया है। `C_(1)` तथा `C_(2)` द्वारा मापे गए सही मान (सेमी में) क्रमशः है
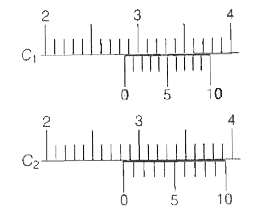
View Solutionदिया है प्रतिरोध `R =(V)/(i)` जहाँ V = `100 +-`5 वोल्ट तथा i = 10 `+-0.2` ऐम्पियर है , तो R में कुल त्रुटि होगी
View Solutionकिसी प्रयोग में सरल लोलक का आवर्तकाल क्रमशः 2.63s,2.56s, 2.42s, 2.71 s तथा 2.80s मापा गया तो औसत निरपेक्ष त्रुटि होगी
View Solutionएक बेलन का व्यास मापने के लिए शून्य त्रुटि रहित एक वर्नियर कैलिपर्स का उपयोग होता है | मापने के दौरान पैमाने का शून्य , मुख्य पैमाने के 5.10 cm और 5.15 cm के बीच में पाया जाता है | वर्नियर पैमाने 50 भाग 2.45 cm के तुल्य है | इस वर्नियर पैमाने का चौबीसवाँ `(24^(th))` भाग मुख्य पैमाने के एक भाग से सटीक सम्पाती होता है | बेलन का व्यास है
View Solutionएक प्रिज्म का कोण नापने में प्रयोग किया गया स्पेक्ट्रोमीटर निम्नलिखित मापन देता है
मुख्य स्केल मापन : 58.5 डिग्री
वर्नियर स्केल मापन : 09 भाग
दिया है - मुख्य स्केल का एक भाग 0.5 डिग्री के बराबर है | वर्नियर स्केल पर कुल भाग 30 है और यह मुख्य स्केल के 29 भागों से मिलते हैं | उपरोक्त आँकड़ों से प्रिज्म का कोण है
View SolutionSearle's प्रयोग द्वारा यंग प्रत्यास्थता गुणांक, `(Y=(4MLg)/(pild)) की तुलना निकालने के लिए एक L = 2m लंबे व d = 30.5mm व्यास के तार का उपयोग किया गया है | भार M = 2.5kg लगाने पर तार की लम्बाई में l = 0.25mm की वृद्धि हुई | d और l को नापने के लिए क्रमशः स्क्रूगेज और माइक्रोमीटर का प्रयोग किया गया | दोनों के पिच 0.5mm एवं दोनों के सरकुलर स्केल पर 100 निशान है | Y के निकाले गये मान में अधिकतम प्रसंभाव्य त्रुटि में
View Solutionसरल लोलक की लम्बाई और आवर्तकाल के मापन में प्रतिशत त्रुटि क्रमशः `1 %` तथा `2 %` है | तब गुरूत्वीय त्वरण के मापन में अधिकतम त्रुटि है
View Solutionएक भौतिक राशि P निम्न सूत्र से प्रदर्शित की जाती है `P=(A^(3)B^((1)/(2)))/(C^(-4)D^((3)/(2)))` तो P में अधिकतम त्रुटि किस राशि के कारण आ सकती है
View Solutionयदि `L = 2.331cm , B = 2.1cm` हो, तो `L + B =`
View Solutionदिये गये अंकों 25.12 , 2009,4.156 एवं `1.217xx10^(-4)` में सार्थक अंकों की संख्या है
View Solutionयदि छड़ A की लम्बाई `3.25 +- 0.01 cm` एवं B की लम्बाई `4.19+- 0.01 cm` है तो छड़ A की तुलना में B की लम्बाई कितना अधिक है
View Solutionएक भौतिक राशि `X=M^(a)L^(b)T^(c)` द्वारा प्रदर्शित है तथा M , L एवं T के मापन में प्रतिशत त्रुटि क्रमशः `alpha, beta व gamma` है , तो X में अधिकतम प्रतिशत त्रुटि होगी
View Solutionएक भौतिक राशि A चार प्रक्षेपित राशियों a,b , c एवं d से व्यजंक `A=(a^(2)b^(3))/(csqrt(d))` द्वारा सम्बन्धित है तथा a, b, c व d के मापन की प्रतिशत त्रुटि क्रमशः `1 % , 3 % , 2 %` एवं `2 %` है तो A में प्रतिशत त्रुटि होगी
View Solutionकिसी प्रयोग में पुल की ऊँचाई ज्ञात करने के लिए , पुल से एक पत्थर छोड़ा जाता है | यह पानी के तल तक पहुँचने में 2s लेता है | यदि समय मापन में होने वाली त्रुटि 0.1 हो तो पुल की ऊँचाई के मापन में त्रुटि होगी
View Solutionदो प्रतिरोधों का मान `R = ( 6 +- 0.3 ) kOmega " और " R = ( 10 +- 0.2) kOmega` है | जब ये दोनों प्रतिरोध समान्तर क्रमे में जोड़े जायें तब तुल्यांकी प्रतिरोध में प्रतिशत त्रुटि होगी
View Solutionवर्नियर कैलीपर्स के मुख्य पैमाने पर 1 mm के चिन्ह है। इसके मुख्य पैमाने के 16 खाने , वर्नियर पैमाने के 20 खानों से सम्पाती होते है। इस वर्नियर कैलीपर्स का अल्पतमांक है :
View Solutionसंख्याओं 23.023 , 0.0003 और `2.1xx10^(-3)` के संगत सार्थक अंक है
View Solutionएक वस्तु प्रारंभ में विराम अवस्था में है | एक विद्यार्थी इस वस्तु के मुक्त - पतन में , किसी दिये गये समय में तय की गई दूरी नापता है और इसका उपयोग गुरूत्वीय त्वरण 'g' का मान ज्ञात करने में करता है | यदि दूरी तथा समय की मापों में अधिकतम प्रतिशत त्रुटि क्रमशः `e_(1)` और `e_(2)` हो तो , g का मान ज्ञात करने में प्रतिशत त्रुटि होगी
View Solutionनिम्नलिखित में असत्य कथन का चयन कीजिये
View Solutionएक ठोस गेंद का घनत्व एक प्रयोग से निर्धारित होना है | गेंद का व्यास एक स्क्रूगेज , जिसका पिच 0.5 mm है तथा जिसके वृत्तीय पैमाने पर 50 भाग है, द्वारा मापा जाता है | माप में गुख्य पैमाने का मान 2.5mm तथा वृत्तीय पैमाने का मान 20 भाग है | यदि गेंद के मापे गये द्रव्यमान में सापेक्ष त्रुटि `2 %` है , तब घनत्व में सापेक्ष त्रुटि है
View Solutionएक तार का व्यास नापने में किये गये स्क्रूगेज के प्रयोग से निम्नलिखित मापन आये :-
मुख्य स्केल पाठ्यांक : 0 मि.मी.
वृत्तीय स्केल पाठ्यांक : 52 भाग
दिया है कि मुख्य स्केल पर 1 मि.मी. वृत्तीय स्केल के 100 भागों के संगत है। उपरोक्त डाटा से तार का व्यास है :
View Solutionकिसी पदार्थ का घनत्व CGS ( सी.जी.एस. ) प्रणाली में `4g//cm^(3)` है , तो ऐसी प्रणाली में , जहाँ लम्बाई का मात्रक 10cm और द्रव्यमान का मात्रक 100g है, घनत्व का मात्रक होगा
View Solutionएक पिण्ड का द्रव्यमान तथा आयतन क्रमश : `5.00 +- 0.05` kg तथा `1.00 +- 0.05m^(3)` प्राप्त होता है | इसके घनत्व में अधिकतम संभावित प्रतिशत त्रुटि होगी
View Solutionएक छात्र एक सरल - आवर्त - दोलन के 100 आवृत्तियों का समय 4 बार मापता है और उनको 90s,91s,95s और 92s पाता है | इस्तेमाल की गई घड़ी का न्यूनतम अल्पांश 0.5s है | तब मापे गये माध्य समय को उसे लिखना चाहिए
View Solutionएक स्क्रू-गेज का पिच 0.5 mm है और उसके वृत्तीय स्केल पर 50 भाग है | इसके द्वारा एक पतली अल्यूमीनियम शीट की मोटाई मापी गई | माप लेने के पूर्व यह पाया गया कि जब स्क्रू गेज के दो जोवो को सम्पर्क में लाया जाता है तब 45 वां भाग मुख्य स्केल लाईन के संपाती होता है और मुख्य स्केल का शून्य ( 0 ) मुश्किल से दिखता है | मुख्य स्केल का पाठ्यांक यदि 0.5mm तथा 25 वां भाग मुख्य स्केल लाईन के संपाती हो , तो शीट की मोटाई क्या होगी
View Solutionकिसी सरल लोलक का आवर्त , `T = 2pisqrt((L)/(g))` है | L का मापित मान g 20.0 cm है , जिसकी यथार्थता 1 mm है | इस लोलक के 100 दोलनों का समय 90s है , जिसे 1s विभेदन की घड़ी से मापा गया है , तो g के निर्धारण में यथार्थता होगी
View Solutionएक व्यक्ति एक पत्थर को कुएं में गिराते समय और कुऐं की तली में संघट से उत्पन्न ध्वनि के समय अंतराल का मापन करके कुएं की गहराई का पता लगाता है | वह समयांतराल के मापन में त्रुटि `deltaT` = 0.01 सेकंड एवं कुऐं की गहराई L=20m मापता है गुरुत्वाकर्षण त्वरण `g = 10ms^(-2)` एवं ध्वनि गति `300ms^(-1)` दी गई है | `(deltaL)/(L)` के मापन में निकटतम आंशिक त्रुटि है
View Solutionघन की आकृति वाले किसी पदार्थ का घनत्व, उसकी तीन भुजाओं एवं द्रव्यमान को माप कर, निकाला जाता है | यदि द्रव्यमान एवं लंबाई को मापने में सापेक्ष त्रुटियाँ क्रमशः `2 %` तथा `1 %` हो तो घनत्व को मापने में अधिकतम त्रुटि होगी
View Solutionकिसी छात्र ने इस्पात की लघु गेंद के व्यास की माप 0.001cm अल्पतमांक वाले स्क्रू गेज द्वारा की | मुख्य पैमाने की माप 5mm और वृत्तीय पैमाने का शून्य संदर्भ लेवल से 25 भाग ऊपर है | यदि स्क्रू गेज में शून्यांक त्रुटि -0.004cm है , तो गेंद का सही व्यास होगा
View Solution
Ordinary Thinking (Objective Questions)(मापन में त्रुटियाँ) questions and complete solutions for chapter मात्रक, विमायें तथा मापन of ERRORLESS PHYSICS (HINDI) of Class 12