Complete Solutions to Ordinary Thinking (आवेश एवं कूलॉम का नियम ) of chapter स्थिर वैद्युत of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | स्थिर वैद्युत |
| ERRORLESS HINDI | Ordinary Thinking (आवेश एवं कूलॉम का नियम ) |
| Number Of Questions | 75 |
| Academic Year | 2023-24 |
विद्युत आवेशों के मध्य लगने वाले बलों से सम्बन्धित नियम है
View Solutionदो समान बिन्दु, जिनमें प्रत्येक पर `3muC` आवेश है, एक निश्चित दूरी (मी. में) पर रखे गये हैं। यदि उन्हें `(hati + hatj + hatk)` तथा `(2hati + 3hatj + 3hatk)`, पर रखा जाता है, तब उनके मध्य उत्पन्न स्थिर वैद्युत बल होगा :
View Solution`5muC` के दो स्थायी आवेश A और B को 6m की दूरी पर रखा गया है। C , A और B को जोड़ने वाली रेखा का मध्य बिन्दु है। एक `-5muC` के आवेश 'Q' को A तथा B को जोड़ने वाली रेखा के लंबवत् C की ओर 0.06 J की गतिज ऊर्जा के साथ छोड़ा जाता है। आवेश 'Q' एक बिन्दु D पर विराम में होगा। CD की दूरी होगी :
View Solutionआवेश `+Q` के कूलम्ब - क्षेत्र के प्रभाव में, इसके चारों ओर एक आवेश - दीर्घवृत्तीय कक्षा में विचरण कर रहा है | तब, सही वक्तव्य/वक्तव्यों का पता लगाएँ
View Solutionधातु के बने R, 2R, 3R त्रिज्या चाले तीन खोखले संकेन्द्री गोलों को क्रमश : `Q_(1) ,Q_(2),Q_(3)` , आवेश दिये जाते हैं | तीनों गोलों की बाहरी सतहों पर आवेश के घनत्व बराबर पाये जाते हैं | तब दिये गये आवेशों का अनुपात `Q_(1):Q_(2):Q_(3)` होगा
View Solutionएक समांतर प्लेट संधारित्र में, प्लेट का क्षेत्रफल A तथा आवेश Q है। अन्य प्लेट पर आवेश के कारण एक प्लेट पर लगने वाला बल बराबर होगा :
View Solutionएक साबुन के बुलबुले को ऋण आवेश दिया गया है , तो उसकी त्रिज्या
View Solutionजब कंघी को सूखे बालों में रगड़ा जाता है तो यह छोटे - छोटे कागज के टुकड़ो को आकर्षित करने लगती है इसका कारण है
View Solutionएक वर्ग के विपरीत कोनों में प्रत्येक पर एक आवेश Q रखा है। दूसरे दो विपरीत कोनों पर आवेश q रखा है। यदि Q पर परिणामी विद्युत बल शून्य है , तब `Q/q` का मान है :
View Solutionदो गोले जिन पर `+6muC` और `+9muC` का आवेश हैं, एक दूसरे से d दूरी पर स्थित है तथा दोनों विरोधी बल F का अनुभव करते है | जब एक `-3muC` का आवेश इसी दूरी पर रखे दोनों गोलों को दिया जाए तब नया विरोधी बल है
View Solutionसमरूप विद्युत क्षेत्र E में आवेश q को प्रक्षेपित किया जाता है | इसके द्वारा Y दूरी तय करने में सम्पन्न कार्य है
View Solutionगतिमान आवेश से सम्बद्ध ऊर्जा का कारण है
View Solutionविद्युत् - क्षेत्र में जा रहे एक आवेशित कण पर लगने वाले विद्युत - बल का परिमाण निर्भर करता है
View Solutionभिन्न आवेश के दो समरूप गोलों को वायु माध्यम में परस्पर d दूरी पर रखने पर वे एक दूसरे को बल F से आकर्षित करते हैं | गोलों को सम्पर्क में लाकर पुनः पूर्व स्थिति में रख दिया जाता है | अब गोले परस्पर प्रतिकर्षण बल आरोपित करने लगते हैं जिसका परिमाण पूर्व में आरोपित आकर्षण बल के बराबर होता है | तब गोलों पर प्रारम्भिक स्थिति के आवेशों का अनुपात होगा
View Solutionजब किसी विधि द्वारा प्राकृतिक धातु प्लेट की सतह से `10^(19)` इलेक्ट्रॉन हटाये जाते है, तब इस पर आवेश होगा
View Solutionएक समान बिन्दु से समान त्रिज्या तथा द्रव्यमान के दो गोलों को समान लम्बाई की दो डोरियों से इस प्रकार लटकाया जाता हैं कि उनकी सतह एक दूसरे को स्पर्श करती है | गोलों पर `4xx10^(-6)C` का आवेश संचित करने पर वे इस प्रकार प्रतिकर्षित होते हैं कि संतुलन में उनकी डोरियों के बीच कोण `60^(@)` हो जाता हैं | यदि डोरियों के बीच बिन्दु से गोले के केन्द्र तक दूरी 10 cm हो तब प्रत्येक गोले का द्रव्यमान ज्ञात कीजिए
`(K=9xx10^(9)` तथा g=10 ms`"^(-2))`
View Solutionत्रिज्या `R_(1)` , के एक ठोस गोले का आयतन आवेश घनत्व `rho=(rho_(0))/(r)` है | इसे एक खोखले गोले जिसकी त्रिज्या `R_(2)` तथा आवेश पृष्ठ घनत्व `sigma` है के अन्दर इस प्रकार रखा गया है कि निकाय का कुल आवेश शून्य होता है | `rho_(0)` एक धनात्मक नियतांक है तथा गोले के केन्द्र से दूरी r है | तब अनुपात `R_(2)/R_(1)` होगा
View Solutionत्रिज्या R के एक ठोस गोलीय चालक में केन्द्र पर त्रिज्या `a( a lt R)` की एक गोलीय गुहा है | केन्द्र पर आवेश + Q रखा जाता है | तब आन्तरिक पृष्ठ , बाह्य पृष्ठ और स्थिति `r(a lt r lt R )` पर आवेश का मान क्रमशः है
View Solutionपृथ्वी के पृष्ठ पर विपरीत ऋणात्मक आवेश `5xx10^(5)C` लगभग है पृथ्वी का आवेश पृष्ठ घनत्व `(C//m^(2) )` लगभग है
View Solutionदो वृत्तीय प्लेटों , जिनके बीच दूरी 5 mm है , से एक समान्तर पट्टिका संधारित्र बनाया गया है। जिसके बीच परावैद्युत स्थिरांक 2.2 का एक परावैद्युत रखा गया है। जब परावैद्युत में विद्युत क्षेत्र `3xx10^(4)V//m` है , तब धनात्मक प्लेट का आवेश घनत्व लगभग होगा :
View Solutionनिम्न में से कौन सा एक विकल्प विद्धुत बल रेखाओं का गुण नही है
View Solutionप्रत्येक मान के दो आवेश x = -a और x = a x- अक्ष पर रखे है | द्रव्यमान m और आवेश `q_(0)=(q)/(2)` का एक कण मूल बिन्दु पर रखा है | यदि आवेश `q_(0)` को y- अक्ष के अनुदिश एक अल्प-विस्थापन `(yltlta)` दिया जाए, तब कण पर कार्यरत , परिणामी बल इसके समानुपाती है
View Solutionसरकंडे ( पिथ ) की दो बॉलों ( गोलियों ) पर समान ( बराबर ) आवेश हैं | इन्हें समान लम्बाई की डोरियों ( धागे से एक बिन्दु से लटकाया गया है | संतुलन की अवस्था में इनके बीच की दूरी r है | दोनों डोरियों को उनकी आधी लम्बाई पर कस कर बाँध दिया जाता है | अब सन्तुलन की स्थिति में दोनों बॉलों के बीच की दूरी होगी
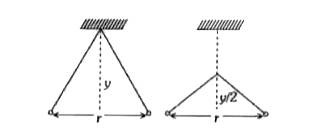
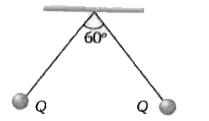
View Solutionदो छोटी गोलाकार गेंदें प्रत्येक पर `Q = 10muC` आवेश है , को दो समान लम्बाई प्रत्येक 1 मीटर, के कुचालक धागों द्वारा छत के किसी बिन्दु से लटकाई गयी है | यह पाया गया है कि साम्यावस्था में धागों के मध्य चित्रानुसार `60^(@)` का कोण है | धागों में तनाव है- (दिया है =`(1)/(4piepsilon_(0))=9xx10^(9)Nm//C^(2)`
View Solutionकिसी वर्ग के चार कोनों पर बिन्दु आवेश `-Q , -q , 2q` तथा 2Q क्रमशः रखे गये हैं | Q तथा q के बीच क्या संबंध होना चाहिये, ताकि वर्ग के केन्द्र पर विभव शून्य हो जाए
View Solutionत्रिज्या r की वलय पर आवेश Q एक समान रूप से वितरित है | इसके केन्द्र पर स्थित आवेश द्वारा अनुभव बल होगा
View Solutionकिसी उदासीन चालक गोले की कल्पना कीजिए | एक धनावेशित बिन्दु आवेश को गोले के बाहर रखा जाता है | तब गोले पर कुल आवेश होता है
View Solutionएक चालक को स्थानांतरित इलेक्ट्रॉनों द्वारा `-3xx10^(-7)` कूलॉम आवेश दिया जाता है। चालक के द्रव्यमान में वृद्धि (किग्रा में) तथा इलेक्ट्रॉनों की संख्या क्रमशः है
View Solutionदो समान आवेशित गोले एक दूसरे से वायु में 0.6m की दूरी पर रखे है इनके बीच लगने वाला प्रतिकर्षण बल 10 mg भार है तब प्रत्येक गोले पर आवेश होगा | `(g=10`मी./से.`"^(2))`
View Solutionनिर्वात् की विद्युतशीलता का मान होता है
View Solutionदो छोटे गोलों के द्रव्यमान `M_(1)` तथा `M_(1)` है, इन्हें `L_(1) व L_(2)` लम्बाई की भारहीन विद्युतरोधी डोरियों से लटकाया गया है | गोलों पर आवेश क्रमशः `Q_(1)` तथा `Q_(2)` है | गोले इस प्रकार लटकाये गये है कि वे एक - दूसरे से समान तल में होते है तथा डोरियाँ ऊर्ध्वाधर से `theta_(1) व theta_(2)` कोण अन्तरित करती है | ( चित्रानुसार ) निम्नलिखित में कौन सी शर्त आवश्यक होगी , यदि `theta_(1)=theta_(2)`

View Solutionएक आवेश Q को दो भागों में q और Q - q में विभाजित किया जाता है | अलग करने पर दोनों आवेशों के बीच का कूलॉम बल अधिकतम तब होगा जब अनुपात `Q//q` का मान होगा
View Solutionएक कूलॉम आवेश में इलेक्ट्रॉनों की संख्या का मान होगा
View Solutionदो समरूप चालक गेंद A व B पर क्रमशः धनात्मक आवेश `q_(1) व q_(2)` है | किन्तु `q_(1) ne q_(2)` है | दोनों बॉल को परस्पर स्पर्श किया जाता है तथा फिर उन्हें पूर्व स्थिति में ही रख दिया जाता हैं | आवेशों के मध्य बल होगा
View Solutionदो `R_(1), R_(2)` त्रिज्या के आवेशित चालक गोलों को एक तार द्वारा जोड़ा गया है | तब गोलों के पृष्ठीय आवेश घनत्वों का अनुपात `sigma_(1)//sigma_(2)` होगा
View Solutionएक धातु के गोले A को धनावेश दिया जाता है जबकि दूसरे अन्य एकसमान धातु के गोले B को उतना ही ऋणावेश दिया जाता है यदि पहले दोनों गोले के द्रव्यमान समान हैं तो बाद में गोले के द्रव्यमान होंगे?
View Solutionएक पिण्ड द्वारा प्रत्येक सेकण्ड में `10^(10)` इलेक्ट्रॉन ग्रहण किये जाते है | कितने समय पश्चात् पिण्ड का आवेश 1 कूलम्ब हो जायेगा
View Solutionएक बिन्दु आवेश q जो कि एक पतली आवेशित छड़ जिसकी लम्बाई L तथा आवेश Q है , के एक सिरे से अक्ष पर 1 दूरी पर रखी है | इसकी लम्बाई के सापेक्ष एक समान विपरित दोनों के मध्य वैद्युत बल का आयाम होगा
View Solutionदो बिन्दु आवेश `+3muC` एवं `+8muC` एक दूसरे को 40N के बल से प्रतिकर्षित करते हैं | यदि `-5muC` का आवेश प्रत्येक में और जोड़ दिया जाये तो इनके मध्य लगने वाला बल हो जायेगा
View Solutionदो प्रोटॉन परस्पर `1xx10^(-10)` से.मी. की दूरी पर है | उन पर क्रियाशील बल है
View Solution10 cm भुजा वाले समबाहु त्रिभुज ABC के शीर्षों पर क्रमशः `1muC, -1muC"` तथा `"2muC` आवेश वायु में रखे गये हैं | शीर्ष C पर स्थित आवेश पर परिणामी बल होगा
View Solution`alpha` - कण पर आवेश है
View Solutionदो समान त्रिज्याओं तथा क्रमशः `+10muc व -20muC` आवेश वाले दो छोटे गोलीय चालक एक दूसरे से R दूरी पर रखे जाने पर `F_(1)` बल अनुभव करते हैं | यदि उनके सम्पर्क में लाकर पुनः उसी दूरी तक पृथक कर देते हैं तो वे `F_(2)` बल अनुभव करते हैं | `F_(1)` का `F_(2)` से अनुपात होगा
View Solutionत्रिज्या ' a ' तथा ' b ' के दो एक - केन्द्री गोलों के ( चित्र देखिये ) बीच के स्थान में आयतन आवेश - घनत्व `rho=(A)/(r)` है , जहाँ A स्थिरांक है तथा r केन्द्र से दूरी है | गोलों के केन्द्र पर एक बिन्दु - आवेश Q है | A का वह मान बतायें जिससे गोलों के बीच के स्थान में एकसमान वैद्युत क्षेत्र हो

View Solutionदो आवेश एक दूसरे से 'd' दूरी पर है | यदि दोनों के मध्य `(d)/(2)` मोटाई की तांबे की प्लेट रख दें तो प्रभावी बल होगा
View Solutionदो इलेक्ट्रॉन एक दूसरे से `1Å` की दूरी पर हैं | इनके बीच कूलॉम बल होगा
View Solutionदो ताँबे की गेंदें , प्रत्येक का भार 10 gm है | एक दूसरे से वायु में 10cm दूर रखी हैं | यदि प्रत्येक `10^(6)` परमाणुओं से एक इलेक्ट्रॉन एक गेंद से दूसरी गेंद की ओर स्थानान्तरित होता है | इनके मध्य कूलॉम बल है | ( ताँबे का परमाणु भार 63.5 है )
View Solutionएक a त्रिज्या वाले ठोस गोलीय चालक पर कुल धनावेश 2Q है | एक गोलीय चालक कोश जिसकी आन्तरिक त्रिज्या b तथा बाहरी त्रिज्या c है , पर कुल आवेश `-Q` है | यह ठोस गोले के साथ संकेन्द्रीय रखा है | गोलीय कोश के आन्तरिक तथा बाह्य पृष्ठों पर पृष्ठीय ओवश घनत्व होंगे
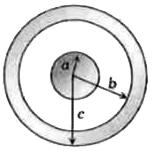
View Solutionतीन आवेश प्रत्येक Q समबाहु त्रिभुज के शीर्षों पर रखे हैं | केन्द्रक पर रखे आवेश q पर विद्युत बल होगा ( त्रिभुज की प्रत्येक भुजा L है )
View Solutionवायु में रखे दो आवेश एक दूसरे को `10^(-4)N` से प्रतिकर्षित करते हैं | दोनों आवेशों के मध्य तेल भर दिया जाये तो बल `2.5xx10^(-5)N` हो जाता है तो तेल का परावैद्युतांक होगा
View Solutionतीन आवेश ' a ' भुजा वाले समबाहु त्रिभुज के शीर्षों पर रखे हैं | शीर्ष A पर रखे आवेश द्वारा अनुभव किया गया बल BC के लम्बवत् दिशा में होगा
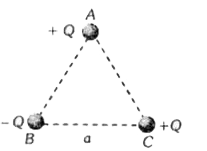
View Solutionदो कण जिनके द्रव्यमान m तथा आवेश q है , एक दूसरे से 16 सेमी. दूर हैं | यदि वे कोई बल अनुभव न करें तो `(q)/(m)` का मान होगा
View Solutionजब काँच की छड़ को सिल्क से रगड़ा जाता है तो यह
View Solutionहाइड्रोजन परमाणु में, r त्रिज्या की कक्षा में एक इलेक्ट्रॉन नाभिक के चारो ओर चक्कर लगाता है इनके मध्य कूलॉम बल `vecF` है ( यहाँ `K=(1)/(4piepsilon_(0)`)
View Solutionकिसी पिण्ड पर `-80muC` आवेश है | इस पर अतिरिक्त इलेक्ट्रॉनों की संख्या है
View Solutionदो बिन्दु आवेशों को हवा में एक निश्चित दूरी r पर रखा जाता है | ये एक - दूसरे की ओर F बल लगाते हैं | तब दूरी r' जिस पर ये आवेश परावैद्युत नियतांक k के माध्यम में समान बल लगाते है , है
View Solutionदो आवेश `+6muC` तथा `+15muC` को x- अक्ष के अनुदिश क्रमशः x = 0 तथा x = 2m पर रखा गया है | एक ऋणात्मक आवेश को इनके मध्य इस प्रकार रखा गया है कि इस पर परिणामी बल शून्य होता है | ऋणात्मक आवेश की दूरी होगी ( d ) स्थिति , आवेश की मात्रा पर निर्भर करती है
View Solutionआवेश `-50e` की एक बॉल को एक खोखले गोले के केन्द्र पर रखा है, जिसका कुल आवेश `-50 e` है | खोखले गोले के बाह्म पृष्ठ पर आवेश होगा
View Solutionपृथक - पृथक् डोरियों से क्रमांक 1 से 5 तक अंकित गेंद लटकायी जाती हैं | युग्म `( 1 , 2 ), ( 2 , 4 )` तथा `( 4 , 1 )` परस्पर वैद्युत स्थैतिक आकर्षण बल दर्शाते हैं जबकि युग्म `( 2 , 3 )` और `( 4 , 5 )` प्रतिकर्षण दर्शाते हैं, तो गेंद क्रमांक 1 होना चाहिये
View Solutiona लम्बाई के एक वर्ग के चारों कोनों A , B , C , D पर समान आवेश q रखे हैं | D पर रखे हुए आवेश पर लगने वाले बल का परिमाण होगा
View Solutionदो धनात्मक आयनों में प्रत्येक का आवेश q तथा d परस्पर व दूरी पर स्थित है | प्रत्येक आयन पर हटाये गये इलेक्ट्रॉन की संख्या क्या होगी , यदि आयनों के मध्य प्रतिकर्षण बल F क्रियाशील हो ( e इलेक्ट्रॉन पर आवेश है )
View Solutionसमान त्रिज्याओं के दो गोलाकार चालकों B एवं C पर आवेश की मात्रा समान है तथा उन्हें एक - दूसरे से कुछ दूर रखने पर उनके बीच लगने वाला प्रतिकर्षण बल F है | उतनी ही त्रिज्या वाले एक अन्य अनावेशित चालक का संपर्क पहले B से कराते हैं और फिर C से संपर्क कराकर उसे हटा दिया जाता है | B तथा C के बीच लगने वाला बल अब कितना होगा
View Solutionजब किसी वस्तु को पृथ्वी से जोड़ा जाये तो पृथ्वी से वस्तु की ओर इलेक्ट्रॉन का प्रवाह होता है | इसका तात्पर्य है कि वस्तु
View Solutionदो आवेशित गोलों पर आवेश क्रमश : `+7muC` एवं `-5muC` हैं , एवं इनके मध्य कार्यरत बल F है | यदि प्रत्येक को `-2muC` का अतिरिक्त आवेश दे दिया जाये तो इनके मध्य नया आकर्षण बल होगा
View Solutionएक दूसरे से `5xx10^(-11)m` की दूरी पर स्थित इलेक्ट्रॉन एवं प्रोटॉन के मध्य स्थिर वैद्युत बल और गुरूत्वाकर्षण बल का अनुपात होगा ( इलेक्ट्रॉन पर आवेश = `1.6 xx 10^(-19)C` , इलेक्ट्रॉन का द्रव्यमान = `9.1 xx 10^(-31) kg` , प्रोटॉन का द्रव्यमान = `1.6xx10^(-27)kg , G = 6.7xx10^(-11)Nm^(2)//kg^(2)`
View Solutionदो आवेशित गोलों पर आवेश क्रमशः `-9muC" एंव "5muC` है इनको आपस में स्पर्श कराकर कुछ दूरी पर रख देते है तो प्रत्येक गोले के लिए निम्न कथनों में सत्य कथन है
View Solutionदो समरूप आवेशित गोले A एवं B , जो एक - दूसरे से एक निश्चित दूरी से विस्थापित है , के बीच F परिमाण का प्रतिकर्षण बल लगता है | समान आकार के एक तीसरे अनावेशित गोले C को गोले A के सम्पर्क में रखकर विलगित किया जाता है तथा इसे A एवं B के मध्यबिन्दु पर रखा जाता है | C गोले पर लगे बल का परिमाण है
View Solutionसमान परिमाण के दो आवेश एक दूसरे से r दूरी पर स्थित हैं और इनके मध्य कार्यरत बल F है | यदि आवेशों के मान आधे कर दिये जायें एवं इनके मध्य की दूरी को दो गुनी कर दी जाये तो इनके मध्य नया बल होगा
View Solution`1muC` के अनन्त आवेश x- अक्ष पर x = 1 , 2,4,8 , ……….. `oo` स्थितियों पर रखे हैं | यदि 1C का आवेश मूल बिन्दु पर स्थित हो तो इस पर आरोपित कुल बल होगा
View Solutionकिसी विद्युत क्षेत्र से संबधित वायुमण्डल का ऊपरी भाग का विभव पृथ्वीतल के सापेक्ष 400kV पर है | उपरोक्त विद्युत क्षेत्र ऊँचाई के साथ घटता जाता है | पृथ्वीतल के निकट विद्युत क्षेत्र `100Vm^(-1)` है | फिर भी, हमें घर से बाहर आने पर झटका नहीं लगता है | क्यों ( मान लो घर एक स्टील का पिंजरा है जिससे की उसके अन्दर विद्युत क्षेत्र नहीं है)
View Solutionचार धात्विक चालकों की निम्न आकृतियाँ हैं
1. गोला
2. बेलन
3. नाशपाती आकार
4. तड़ित चालक यदि इन्हें एक कुचालक आधार पर रखकर आवेशित किया जाये तो किस पर लम्बे समय तक आवेश रहेगा
View Solutionनिम्न में से गलत कथन चुनें | कूलॉम का नियम उस विद्युत बल को सही परिभाषित करता है , जो
View Solutionनिम्न कथनों में कौनसा कथन कूलाम के नियमों को दर्शाता है
View Solutionकिसी उभयनिष्ठ बिन्दु से लम्बाई l की दो द्रव्यमानहीन डोरियों से निलंबित, दो सर्वसम आवेशित गोले , अन्योन्य प्रतिकर्षण के कारण , आरम्भ में एक दूसरे से `d ( d ltltl )` दूरी पर है | दोनों ही गोलों से एक नियत दर से आवेशों का क्षरण आरम्भ होता है , और इसके परिणामस्वरुप गोले एक दूसरे की ओर वेग v से आते हैं | तब गोलो के बीच की दूरी , x के फलन के रूप में वेग का विचरण किस रूप में होता है
View Solutionकल्पना कीजिए कि एक प्रोटॉन और एक इलेक्ट्रॉन के आवेश में अल्प अन्तर होता है | इनमें से एक `-e` है और दूसरा `(e + Deltae )` है | यदि एक दूसरे से d दूरी पर रखे हाइड्रोजन के दो परमाणुओं के बीच (जहाँ d परमाणु के साइज से बहुत अधिक है ) स्थिर वैद्युत बल और गुरूत्वीय बल का परिणामी ( नेट ) शून्य है तो , `Deltae` की कोटि होगी
View Solution
Ordinary Thinking (आवेश एवं कूलॉम का नियम ) questions and complete solutions for chapter स्थिर वैद्युत of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS स्थिर वैद्युत
- Assertion & Reason
- Critical Thinking
- Graphical Questions
- JEE Section (Comprehension type questions)
- JEE Section (Integer type questions)
- JEE Section (JEE (Advanced) 2018)
- JEE Section (Matrix Match type questions)
- JEE Section (More than one correct answers)
- JEE Section (Reasoning type questions)
- Ordinary Thinking (आवेश एवं कूलॉम का नियम )
- Ordinary Thinking (धारिता)
- Ordinary Thinking (विद्युत क्षेत्र एवं विभव )
- Ordinary Thinking (विद्युत फ्लक्स एवं गॉस नियम)
- Ordinary Thinking (वैद्युत द्विध्रुव)
- Ordinary Thinking (संधरित्रों का संयोजन)
- Self Evaluation Test