Complete Solutions to Ordinary Thinking (विद्युत क्षेत्र एवं विभव ) of chapter स्थिर वैद्युत of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | स्थिर वैद्युत |
| ERRORLESS HINDI | Ordinary Thinking (विद्युत क्षेत्र एवं विभव ) |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
दो समान आवेश Q परस्पर कुछ दूरी पर रखे हैं इनको मिलाने वाली रेखा के केन्द्र पर q आवेश रखा गया है | तीनों आवेशों का निकाय सन्तुलन में होगा यदि का q मान हो
View Solutionत्रिज्या R और कुल आवेश Q वाले एक ठोस गोले पर आवेश घनत्व वितरण `P(r)=(Q)/(piR^(4))r` है , गोले के केन्द्र से `r_(1)` दूरी पर गोले के अन्दर एक बिन्दु ' p ' पर विद्युत क्षेत्र का परिमाण है
View Solutionदो छोटे गोलाकार परस्पर r दूरी पर रखे गये हैं | प्रत्येक पर q वैद्युत आवेश है | यदि एक गोलाकार को दूसरे गोलाकार के चारों ओर r त्रिज्या के वृत्तीय पथ पर घुमाया जाता है तो सम्पन्न कार्य होगा
View Solutionदो बिन्दुओं P एवं Q के विभवों को क्रमशः 10V एवं -4V पर बनाए रखा जाता है | 100 इलेक्ट्रॉनों को P से Q तक ले जाने में किया गया कार्य है
View Solutionएक इलेक्ट्रॉन जिसका द्रव्यमान m तथा आवेश q है वह E वैद्युत क्षमता वाले क्षेत्र में विराम अवस्था से गतिशील हो जाता है | तो इसे `l` दूरी तय करने के लिए इसे कितने वेग की आवश्यकता होगी
View Solutionएकसमान आवेशित गोलाकार कोश के भीतर वैद्युत क्षेत्र की तीव्रता होती है
View Solutionकिसी भी बिन्दु x,y,z ( सभी मीटरों में ) विद्युत विभव `V = 4x^(2)` वोल्ट द्वारा दिया जाता है | बिन्दु (1m, 0,2m ) पर विद्युत क्षेत्र वोल्ट/मीटर होगा
View Solutionएक 5 सेमी त्रिज्या के खोखले गोलाकार को 10 वोल्ट तक आवेशित किया जाता है | गोलाकार के केन्द्र पर विद्युत विभव होगा
View Solutionजब एकांक धन आवेश को समविभव सतह पर एक बिन्दु से दूसरे बिन्दु तक ले जाते है , तो
View Solutionदो बड़ी ऊर्ध्वाधर (vertical ) व समांतर धातु प्लेटों के बीच 1cm की दूरी है | वे X विभंवातर के DC स्त्रोत से जुड़ी हैं | दोनों प्लेंटो के मध्य एक प्रोटॉन को स्थिर अवस्था में छोड़ा जाता है | छोड़े जोने के तुरंत बाद प्रोटॉन ऊर्ध्व से `45^(@)` कोण बनाता हुआ गति करता है | तब का मान लगभग है
View Solutionएक आदर्श चालक के समीपवर्ती बाहर किसी बिन्दु पर विद्युत क्षेत्र `vecE` होता है
View Solutionचित्र में प्रदर्शित X - Y अक्ष के केन्द्र पर एक आवेश +q रखा गया है | सीधी रेखा AB के अनुदिश , आवेश Q को A से B तक ले जाने में किया गया कार्य होगा
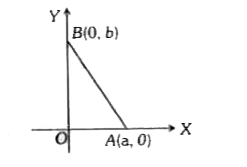
View Solutionयदि एक समबाहु त्रिभुज के तीनों शीर्ष पर `2q , -q ,-q` आवेश क्रमशः स्थित हैं , तो त्रिभुज के केन्द्र पर
View Solutionकिसी भी आकार के एक आवेशित चालक के बाहरी पृष्ठ के पास किसी बिन्दु पर , विद्युत क्षेत्र की तीव्रता `E_(1)` है | एक समान आवेशित अनंत पतली समतल चादर के कारण विद्युत क्षेत्र की तीव्रता `E_(2)` है तो `E_(1)` तथा `E_(2)` में संबंध होगा
View SolutionABC एक समबाहु त्रिभुज है | प्रत्येक शीर्ष पर +q आवेश रखा गया है | बिन्दु O पर वैद्युत क्षेत्र की तीव्रता होगी
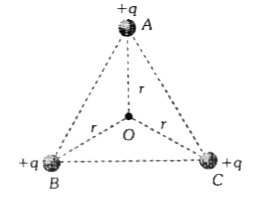
View Solution1cm तथा 3cm त्रिज्या के धातु के दो गोलों को क्रमशः `-1xx10^(-2)C` तथा `5xx10^(-2)C` आवेश दिया गया है | यदि इनको एक चालक तार से जोड़ दिया जाए तो , बड़े गोले पर अन्तिम आवेश होगा
View Solutionवैद्युत क्षेत्र की तीव्रता का परिमाण E इस प्रकार है कि उसमें रखे इलेक्ट्रॉन पर उसके भार के तुल्य बल लगता है | यह वैद्युत क्षेत्र होगा
View Solutionतीन संकेद्रीय गोलीय कोश की त्रिज्याएँ a, b व `c(altbltc)` हैं तथा इनके आवेश पृष्ठ घनत्व क्रमशः `sigma, -sigma व sigma` हैं | यदि `V_(A), V_(B) व V_(C)` तीनों गोलीय कोश के विभव हों , तब c = a + b , के लिये है
View Solutionएक इलेक्ट्रॉन और एक प्रोटॉन एकसमान वैद्युत क्षेत्र में रखने पर उनके त्वरण का अनुपात होगा
View Solutionदो आवेश `+6muC` तथा `-4muC` को 15 cm की दूरी पर रखा जाता है जैसा कि दर्शाया गया है | A के दाएँ से कितनी दूरी पर , वैद्युत-स्थैतिक विभव शून्य होगा ( दूरी cm में )
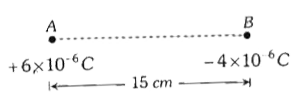
View Solutionनिम्न में से सही संबंध है
View Solutionएक बिन्दु ( x , y , z ) पर वैद्युत विभव `V = -x^(2)y –xz^(3) +4` है | इस बिन्दु पर वैद्युत क्षेत्र `vecE` होगा
View Solutionएक प्रोटॉन और एक इलेक्ट्रॉन को एक समान विद्युत क्षेत्र में रखा जाए तब
View Solutionएक धातु में इलेक्ट्रानों का माध्य मुक्त पथ `4xx10^(-8)m` हैं | वह विद्युत - क्षेत्र जो धातु में किसी इलेक्ट्रान को औसत रूप में 2eV की ऊर्जा प्रदान कर सके , `V//m` की मात्रकों में होगा
View Solutionयदि किसी स्थिर - विद्युत क्षेत्र में E विद्युत क्षेत्र की तीव्रता हो तो स्थिर विद्युत ऊर्जा घनत्व समानुपाती होगा
View Solutionकिसी चालक को दिया गया आवेश उसकी बाह्य सतह पर स्थित होता है क्योंकि
View Solutionएक लकड़ी का गुटका एक घर्षण-रहित तल पर आवृत्ति `v_(0)` से सरल आवर्त दोलन ( SHM ) करता है | गुटके के ऊपर पृष्ठ पर +Q आवेश है | तब एकसमान वैद्युत क्षेत्र `vecE` लगाये जाने पर ( चित्र देखिये ) गुटके का सरल आवर्त दोलन होगा
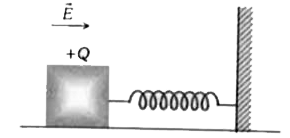
View Solutionधातु का एक अनावेशित गोला दो आवेशित प्लेटों के बीच चित्र के अनुसार रखा गया है वैद्युत बल रेखाओं की प्रकृति किस प्रकार की होगी

View Solutionचित्र में `+Q` आवेश घन के एक किनारे पर स्थित है | तब आवेश `+Q` के कारण घन पर विद्युत अभिवाह का मान है
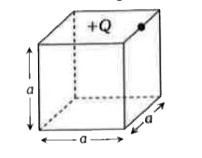
View Solutionएक बिन्दु आवेश q को त्रिज्या r वाले एक वृत्त में Q आवेश के चारों ओर घुमाने में किया गया कार्य होगा
View Solutionदो समान्तर धात्विक प्लेटों का आवेश `+Q` तथा `-Q` है | प्लेटें एक निश्चित दूरी पर परस्पर सम्मुख स्थित है | प्लेटों को केरोसिन तेल में डुबा दिया जाता है | प्लेटों के मध्य विद्युत क्षेत्र .....?
View Solutionकिसी 0.1m त्रिज्या के गोलीय चालक के पृष्ठ पर `0.036N//C` का विद्युत क्षेत्र उत्पन्न करने के लिए इस पर रखे गये इलेक्ट्रोनों की संख्या
View Solutionएक लम्बे बेलनाकार कोश के ऊपरी आधे भाग में धनात्मक पृष्ठ आवेश `sigma` तथा निचले आधे भाग में ऋणात्मक पृष्ठ आवेश `-sigma` है | इस बेलन के चारों ओर विद्युत क्षेत्र - रेखाएँ , यहाँ दर्शाये गये आरेखों में से किस आरेख के समान होगी ( यह आरेख केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं है )
View Solutionचित्र में दर्शाये गए दो बिन्दु आवेश `+10^(-7)C` तथा `-10^(-7)C` को A तथा B पर रखा गया है जिनके बीच की दूरी `20 cm` है | तब बिन्दु पर विद्युत क्षेत्र की गणना कीजिए जो कि A और B दोनों से `20 cm` की दूरी पर है
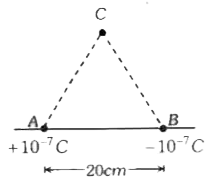
View Solutionयदि एक रेखीय समदैशिक परावैद्युत को विद्युत क्षेत्र की तीव्रता E में रखा जाता है | तब उसका धुवण P होगा
View Solutionकिसी निश्चित क्षेत्र में विद्युत क्षेत्र की तीव्रता `vecE=5hati-3hatjkV//m` दी गयी है | बिन्दु A तथा B जिनके निर्देशांक क्रमशः (4,0, 3) m तथा ( 10,3,0 ) m हैं , के मध्य विभवांतर `V_(B) – V_(A)` होगा
View Solutionएकसमान पृष्ठ आवेश घनत्व वाले चालक पृष्ठ के निकट वैद्युत क्षेत्र
View Solution`2sqrt(2)` मी. भुजा के एक चतुर्भुज के चारों कोनों पर `1muC` आवेश रखा गया है | विकर्णो के कटान बिन्दु पर विभव की मात्रा होगी `(K = 9xx10^(9) SI` इकाई)
View Solutionएक छड़ x- अक्ष के अनुदिश रखी हुई है | जिसका एक सिरा केन्द्र पर तथा दूसरा सिरा `xrarroo` पर है | उस पर एक समान आवेश `lambda//m` लगाया जाता है | बिन्दु x = -a पर अक्ष के सापेक्ष विद्युत क्षेत्र होगा
View Solutionएक कण `A , +q` आवेश व कण `B, +4q` आवेश रखता है | प्रत्येक का द्रव्यमान m है | जब समान विभवान्तर द्वारा विराम अवस्था से गिराया जाये, तो इनकी चालों का अनुपात `(v_(A))/(v_(B))` हो जायेगा
View SolutionR त्रिज्या के किसी आवेशित चालक गोलीय कोश ( खोल) के केन्द्र `(3R)/(2)` से दूरी पर विद्युत क्षेत्र है | इसके केन्द्र से `(R)/(2)` दूरी पर विद्युत क्षेत्र होगा
View Solutionएक बिन्दु द्विध्रुव किसी दिशा निर्धारक के केन्द्र बिन्दु पर स्थित है| x - y समतल में बिन्दु (10 cm, 10 cm) पर विद्युत क्षेत्र की तीव्रता का परिमाण `1.0xx10^(-3)V//m` है | तब बिन्दु (20 cm, 20 cm) पर विद्युत क्षेत्र की तीव्रता का परिमाण होगा
View Solutionएक आदर्श चालक के लिए निम्न में से कौन सा कथन असत्य है
View Solutionविद्युत बल रेखाओं के लिए निम्न में से असत्य कथन है
View Solutionप्रत्येक लम्बाई 1 cm के दो छोटे छड़ चुम्बकों के चुम्बकीय आघूर्ण क्रमशः `1.20 Am^(2) एवं 1.00 Am^(2)` है | इनके N धुवों को दक्षिण की ओर इंगित कर एक दूसरे के समान्तर इन्हें एक क्षैतिज मेज पर रखा गया है | इनकी एक उभयनिष्ठ चुम्बकीय मध्य रेखा है | और इनके बीच की दूरी 20.0cm है | इनके केन्द्रों को जोड़ने वाली रेखा के मध्य बिन्दु O पर परिणामी क्षैतिज चुम्बकीय प्रेरण का मान लगभग है ( पृथ्वी के चुम्बकीय प्रेरण का क्षैतिज घटक `3.6xx10^(-5)Wb//m^(2)`)
View Solutionकिसी बिन्दु आवेश से एक निश्चित दूरी पर विद्युत क्षेत्र `500V //m` तथा विभव 3000V है | यह निश्चित दूरी क्या है
View Solutionपारे की 27 एक समान बूंदें , एक ही समय पर , 10Volt के समान विभव से आवेशित की गयी है | माना कि बूंद का आकार गोलीय है | यदि सभी बूंदें मिलकर एक बड़ी बूंद का निर्माण कर लें , तब इस बड़ी बूंद का विभव होगा
View Solutionएक आवेशित अनन्त चालक तल पर एक रेखा AA' है जो कागज के तल के लम्बवत् है | समतल पर आवेश का पृष्ठ घनत्व `sigma` है और B एक गेंद है जिसका द्रव्यमान m तथा आवेश परिमाण q है | B को डोरी से AA ' रेखा पर एक बिन्दु से बांधा गया है तब सरल रेखा AA' और डोरी के बीच निर्मित स्पर्श रेखा का कोण `(tan theta)` है
View Solutionएक बिन्दु आवेश Q , एक एकसमान रेखीय आवेश घनत्व `lambda` वाले अनन्त लम्बाई के तार तथा एक एकसमान पृष्ठ आवेश घनत्व `sigma` वाले अनन्त समतल चादर के कारण r दूरी पर विद्युत क्षेत्र की तीव्रतायें क्रमश : `E_(1)(r), E_(2)( r ) "तथा" E_(3)(r )` हैं यदि एक दी गई दूरी `r_(0)` पर `E_(1)( r_(0)) =E_(2)( r_(0))=E_(3)(r_(0) )` तब
View Solution30 सेमी दूर पर 2 न्यूटन/कूलॉम मान का विद्युत क्षेत्र उत्पन्न करने वाले बिंदु आवेश का मान क्या होगा|
`[1//4piepsilon_(0)=9xx10^(9)` न्यूटन मी`""^(2)//`कूलॉम`""^(2)]`
View Solutionदो आवेश `+q` और `-q` एक निश्चित दूरी पर हैं, उनके बीचों बीच स्थित बिन्दु पर
View Solutionत्रिज्या `R_(1)` तथा `R_(2)` के दो आवेशित गोलों का आवेश पृष्ठ घनत्व समान है | इनके विभवों का अनुपात है
View Solutionसमरूप विद्युत क्षेत्र `1.6xx10^(5) Vm^(-1)` में स्थित - कण का द्रव्यमान `6.4 xx10^(-27)kg` तथा आवेश `3.2xx xx10^(-19)C` है | विराम स्थिति से `2xx10^(-2)` m का पथ तय करने के बाद कण का वेग होगा
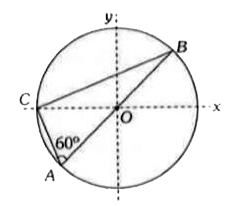
View Solutionचित्रानुसार एक निकाय के तीन बिन्दुओं A , B व C पर आवेश क्रमशः `(q)/(3), (q)/(3) और -(2q)/(3)` स्थित है | बिन्दु O को R त्रिज्या के वृत का केन्द्र और कोण CAB = `60^(@)` लेने पर ,
View Solution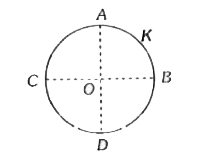
R त्रिज्या की पतली चालकीय रिंग को +Q आवेश दिया जाता है वलय के केन्द्र O पर वलय के AKB भाग के आवेश के कारण विद्युत क्षेत्र E है , वलय के केन्द्र पर ACDB भाग के आवेश के कारण वैद्युत क्षेत्र होगा
View Solutionसंलग्न चित्र में दशाए गएतान परावधुत गाला पर , जिनकी त्रिज्याएँ क्रमशः `R//2`, R तथा 2R है , आवेश Q , 2Q तथा 4Q क्रमशः समान रूप से वितरित है | यदि बिन्दु P , जो प्रत्येक गोले के केन्द्र से R दूरी पर है , पर गोले 1 , 2 तथा 3 के कारण विद्युत क्षेत्र का परिमाण क्रमशः `E_(1)E_(2) तथा E_(3)` है तब
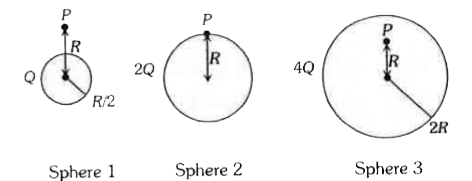
View SolutionR त्रिज्या के एक गोले की सतह पर विद्युत आवेश Q की मात्रा उपस्थित है | तब इस निकाय की विद्युत विभव ऊर्जा होगी
View Solutionएक चालक गोले की त्रिज्या R है | इस पर Q आवेश है | गोले के केन्द्र पर विद्युत विभव तथा विद्युत क्षेत्र क्रमशः है
View Solutionमान लें व्योम में एक विद्युत क्षेत्र `vecE = 30x^(2)hati` है | तब विभवान्तर `V_(A) – V_(0)` , जहाँ `V_(0)`, मूलबिन्दु पर विभव एवं `V_(A)`, x = 2m पर विभव है
View Solutionएक गोलीय कोश की त्रिज्या 10 सेमी. तथा आवेश q है | यदि गोलीय कोश के केन्द्र से 5 सेमी. , 10 सेमी. तथा 15 सेमी. की दूरी पर विद्युत विभव क्रमशः `V_(1) , V_(2) , V_(3)` हो तब
View Solutionदो चालक गोलों की त्रिज्यायें 3 cm तथा 1cm है , इन्हें मुक्त आकाश में परस्पर 10 cm की दूरी पर रखा गया है | यदि प्रत्येक गोलों को 10v के समान विभव से आवेशित किया जाये , तब इनके मध्य प्रतिकर्षण बल होगा
View Solutionविद्युत क्षेत्र की तीव्रता E वाले स्थान पर इसके कारण ऊर्जा घनत्व का मान ( निर्वात् में ) होगा
View Solutionभिन्न - भिन्न अर्धव्यासों के दो गोलों को समान आवेश दिया जाता है I तो विभव का मान
View Solutionमुक्त क्षेत्र के किसी बिंदु पर Q कूलम्ब आवेश के कारण वैधुत विभव `Qxx10^(11)`वोल्ट है | इस बिंदु पर वैद्युत क्षेत्र है |
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजा BC और AC , 2a है | इसके प्रत्येक कोने पर +q आवेश स्थित है | बिन्दु D और E क्रमशः भुजाओं BC और CA के मध्यबिन्दु है | तो D से E तक किसी आवेश को ले जाने में किया गया कार्य होगा
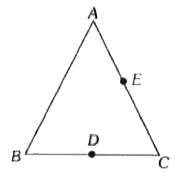
View Solutionवैद्युत विभव एवं दूरी ( x ) के बीच सम्बन्ध को निम्न रूप में दर्शाया गया है `V= ( 5x^(2) + 10x - 9 )` वोल्ट | x = 1 मीटर पर वैद्युत क्षेत्र का मान होगा
View Solutionगलत कथन का चयन कीजिए
View Solutionचित्र में दिखाये गये अनुसार 2L भुजा के एक वर्ग के चार कोनों पर `+q , +q , -q` और `-q` आवेश स्थित हैं, दो आवेश `+q` और `+q` के बीच के मध्य बिन्दु A पर विद्युत विभव है
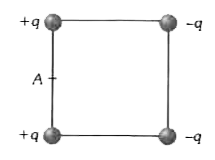
View Solutiona तथा b त्रिज्या के दो गोले आवेशित करने के पश्चात एक तार के द्वारा जोड़ दिये जाते हैं | गोलों की विद्युत क्षेत्र की तीव्रताओं का अनुपात होगा
View Solutionएक कण जिसका द्रव्यमान m तथा आवेश q है किसी एकसमान विद्युत क्षेत्र E में स्थिर है फिर इसे मुक्त कर दिया जाये तो y दूरी चलने के पश्चात इसके द्वारा प्राप्त गतिज ऊर्जा होगी
View Solutionमाना एक विद्युत क्षेत्र `vecE = E_(0) hatx` , जहाँ `E_(0)` स्थिरांक है | इस वैद्युत क्षेत्र के कारण चित्र में दर्शाये आच्छादित क्षेत्र से गुजरने वाली वैद्युत फ्लक्स है
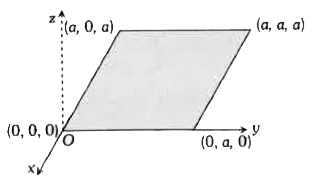
View Solutionएक समान परिमाण के विद्युत क्षेत्र `2xx10^(4)N//C` में एक इलेक्ट्रॉन विराम अवस्था से 1.5cm दूरी गिरता है | इलेक्ट्रॉन को इस दूरी से गिरने में लगा समय होगा
View Solutionएक घन जिसकी प्रत्येक भुजा की लम्बाई b है | इसके प्रत्येक कोने पर आवेश q रखा है , इस आवेश वितरण के कारण घन के केन्द्र पर विद्युत क्षेत्र का मान होगा
View Solutionएक इलेक्ट्रॉन का त्वरण दिये गये कूलम्बियन बल के प्रभाव में `2.5xx10^(22)m//s^(2)` है | तब एक प्रोटॉन का त्वरण समान बल के प्रभाव में लगभग होगा
View Solutionअसत्य कथन चयनित कीजिये
View Solutionएक ऋण आवेशित तेल बूंद को `100Vm^( -1)` के ऊर्ध्वाधर विद्युत क्षेत्र द्वारा गुरूत्वीय प्रभाव में गिरने से स्थिर रखा गया है | बूंद का द्रव्यमान `1.6xx10^(-3)`g हो , तब बूँद पर इलेक्ट्रॉन की संख्या होगी
View Solutionएक समान आवेश Q तथा त्रिज्या R के पहले गोलीय खोल के केन्द्र से दूरी पर विद्युत विभव है
View Solutionदो बिन्दु आवेश `20muC` एवं `80muC` एक - दूसरे से 10 cm की दूरी पर रखे हैं | इन दोनों को जोड़ने वाली रेखा पर `20muC` से कितनी दूरी पर विद्युत क्षेत्र की तीव्रता शून्य होगी
View Solutionमाना R त्रिज्या की एक पतली गोलीय कोश है जिसका एकसमान आवेश पृष्ठ घनत्व `sigma`है | केन्द्र से x दूरी पर कोश के बाहर एक बिन्दु पर विद्युत क्षेत्र है
View Solutionयदि किसी आवेशित गोलीय चालक जिसकी त्रिज्या 10cm है के केन्द्र से 5cm की दूरी पर विभव V है , तो इसके केन्द्र से 15cm दूरी पर विभव होगा
View Solutionचित्रानुसार समरूप विद्युत क्षेत्र की तीव्रता E प्रदर्शित है | पूर्णतः छायांकित बिन्दु के समान कितने बिन्दुओं पर विद्युत विभव समान होगा
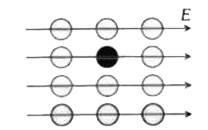
View Solutionदो धनात्मक आवेशों के कारण विद्युत बल रेखायें चित्र में प्रदर्शित हैं | बिन्दुओं A , B तथा C पर क्रमशः विद्युत क्षेत्र `E_(A) , E_(B)` तथा `E_(C)` के परिमाण परस्पर सम्बन्धित है
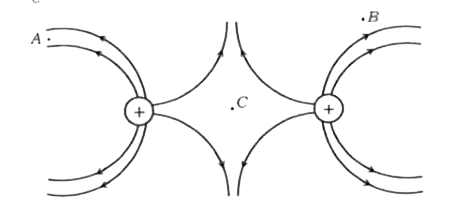
View Solutionएक लम्बा खोखला चालक बेलन समाक्षी रूप एक अधिक त्रिज्या के खोखले चालक बेलन के अन्दर रखा जाता है | दोनों बेलन प्रारम्भ में विद्युतीय उदासीन है
View Solutionx- अक्ष पर स्थित कुछ आवेश के कारण बिन्दु पर विभव `V ( x ) = 20/( x^(2)-4 )` वोल्ट है | तब x = `4` माइक्रोमीटर पर वैद्युत क्षेत्र है
View Solutionइकाई धन आवेश को अनन्त से धनात्मक आवेश Q से x दूरी पर एक बिन्दु तक लाने में सम्पन्न कार्य W है | तब इस बिन्दु पर विभव `phi` होगा
View SolutionA , B तथा C किसी एकसमान विद्युत क्षेत्र में तीन बिन्दु हैं | विद्युत विभव का मान

View Solutionवर्ग के चारों कोनों पर आवेश रखे गये है ( जैसा चित्र में दर्शाया गया है ) इसके केन्द्र पर वैद्युत क्षेत्र की तीव्रता `vecE` एवं विभव V है | यदि बिन्दु A और B के आवेश क्रमशः बिन्दु D व C के आवेशों के साथ बदल दिये जायें तब
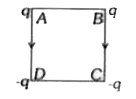
View SolutionX - Y तल के मूल बिन्दु (0,0 ) पर `10^(-3)muC` का आवेश रखा है | बिन्दु A और B क्रमशः निर्देशांक (sqrt(2) , sqrt(2)) एंव ( 2,0 ) पर स्थित है | तब A और B के मध्य विभान्तर होगा
View Solution`sqrt(2)` मी. भुजा वाले वर्ग के शीर्षों पर `+10muC , +5muC , -3muC` तथा + `8muC` आवेश रखे गये हैं | वर्ग के केन्द्र पर विभव होगा
View Solutionनिम्न चित्र में एक बिन्दु आवेश को बिन्दु P से A , B तथा C तक लाने में कार्य क्रमशः `W_(A),W_(B) `तथा `W_(C)` है , तब

View Solutionएक आवेश के कारण इससे 3 मी , की दूरी पर उत्पन्न विद्युत क्षेत्र `200N//C` है | आवेश का परिमाण है `[(1)/(4piepsilon_(0))=9xx10^(9)(N-m^(2))/(C^(2))]`
View Solution0.2 मी, भुजा वाले एक समबाहु त्रिभुज के दो शीर्षों A व B पर प्रत्येक `4muC` के आवेश वायु में रखे हैं | शीर्ष C पर विद्युत विभव `[(1)/(4piepsilon_(0))=9xx10^(9)(N-m^(2))/(C^(2))]`
View Solution`5muC` के बिन्दु आवेश से 80 सेमी. दूर किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता होगी
View SolutionR त्रिज्या के वृत्त पर 10 इलेक्ट्रॉन एक दूसरे से समान दूरी पर स्थित हैं | अनन्त पर V = 0 के सापेक्ष केन्द्र C पर विद्युत विभव V व विद्युत क्षेत्र E होंगे
View Solutionदो धनात्मक बिन्दु आवेश `12muC व 8muC` एक दूसरे से 10 सेमी. दूरी पर रखे हैं | इन्हें 4 सेमी. तक पास लाने में किया गया कार्य होगा
View Solutionतीन एकसमान बिन्दु आवेश चित्रानुसार एक समकोण समद्विबाहु त्रिभुज के शीर्षों पर रखे गये हैं | विकर्ण के मध्य बिन्दु पर कौनसा सदिश विद्युत क्षेत्र की दिशा से संपाती होगा
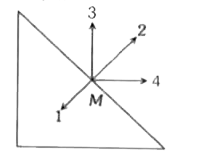
View Solutionविद्युत क्षेत्र `vecE = e_(1)hati + e_(2)hatj + e_(3)hatk` में आवेश Q का विस्थापन `vecr = ahati + bhatj` है | तो किया गया कार्य है
View Solutionएक इलेक्ट्रॉन विराम से 50V विभव वाले बिन्दु से 70V विभव वाले बिन्दु तक गति करता है , अंतिम अवस्था में इसकी गतिज ऊर्जा होगी
View Solutionएक `R` त्रिज्या के ठोस गोले पर एकसमान रूप से आवेश वितरित है | विद्युत क्षेत्र `E` ( गोले के अन्दर ) तथा गोले की त्रिज्या `R` में सम्बन्ध है
View Solutionदो आवेश `+5muC` तथा `+10muC` एक दूसरे से 20 cm दूर रखे हैं | इन आवेशों को जोड़ने वाली रेखा के मध्य बिन्दु पर कुल विद्युत क्षेत्र है
View Solution
Ordinary Thinking (विद्युत क्षेत्र एवं विभव ) questions and complete solutions for chapter स्थिर वैद्युत of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS स्थिर वैद्युत
- Assertion & Reason
- Critical Thinking
- Graphical Questions
- JEE Section (Comprehension type questions)
- JEE Section (Integer type questions)
- JEE Section (JEE (Advanced) 2018)
- JEE Section (Matrix Match type questions)
- JEE Section (More than one correct answers)
- JEE Section (Reasoning type questions)
- Ordinary Thinking (आवेश एवं कूलॉम का नियम )
- Ordinary Thinking (धारिता)
- Ordinary Thinking (विद्युत क्षेत्र एवं विभव )
- Ordinary Thinking (विद्युत फ्लक्स एवं गॉस नियम)
- Ordinary Thinking (वैद्युत द्विध्रुव)
- Ordinary Thinking (संधरित्रों का संयोजन)
- Self Evaluation Test