Complete Solutions to प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प of chapter धारिता और परावैधुत पदार्थ of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | धारिता और परावैधुत पदार्थ |
| GRB PUBLICATION HINDI | प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
एक प्रोटॉन और एक इलेक्ट्रॉन , एकसमान वैधुत क्षेत्र में रखे जाते हैं।
View Solutionएक बिंदु आवेश , वैधुत क्षेत्र में लाया जाता है। किसी नजदीकी बिंदु पर वैधुत क्षेत्र
View Solutionकिसी स्थान पर वैधुत क्षेत्र बाहरी की ओर है और मूल बिंदु से r दूरी के अनुपाती है। मूल बिंदु पर वैधुत विभव को शून्य लेते हुए
View Solutionएक धातु का ठोस गोला , एकसमान वैधुतक्षेत्र में रख दिया जाता है। बल रेखाएँ , चित्र I.36 में दिखाए पथ /पथो पर चलती हैं
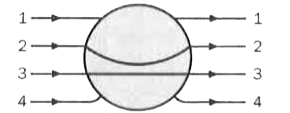
View Solutionएक आवेशित बेलनाकार संधारित्र के वलयाकार क्षेत्र में वैधुत क्षेत्र `vecE` का परिमाण
View SolutionR व्यासार्ध का एक धनात्मक आवेशित पतला धातु का रिंग , XY - तल में इसके केंद्र को मूल बिंदु O पर टिकाते हुए रखा जाता है। एक ऋणात्मक आवेशित कण `P,(0,0,x_(0))` बिंदु पर स्थिर अवस्था से छोड़ा जाता है जहाँ `z_(0)gt0` है। तब P की गति
View SolutionR व्यासार्ध का एक अचालक ठोस गोला , एकसमान रूप से आवेशित है। इससे गोले के केंद्र से r दुरी पर वैधुत क्षेत्र का परिणाम
View Solutionचित्र I.37 में किसी क्षेत्र की बल रेखा दिखाई गई है। निम्न विकल्पों में से यह कभी भी प्रदर्शित नहीं करेगा

View Solution`+q` का एक आवेश `x=x_(0),x=3x_(0),x=5x(0),...,oo` तक हर बिंदु पर X - अक्ष पर रखा जाता है और -q का एक आवेश, `x=2x_(0),x=4x_(0),x=6x_(0),..,oo` तक हर बिंदु पर रखा जाता है। यहाँ `x_(0)` एक धनात्मक नियतांक है। किसी आवेश Q इससे r दुरी पर किसी बिंदु पर वैधुत विभव `(1)/(4piepsilon_(0))(Q)/(r)` ले। तब उपरोक्त आवेश समूहों के कारण मूल बिंदु पर विभव है।
View Solutionनिम्न में से कौन - सी राशियाँ , शून्य विभव या शून्य स्थितिज ऊर्जा के चयन पर निर्भर नहीं करती ?
View SolutionQ आवेश वाला एक ठोस चालक गोला , चारों ओर से एक अनावेशित संकेन्द्री चालक गोलीय खोल से घिरा हुआ है। मान लें कि ठोस गोले के पृष्ठ ओर गोलीय खोल के बाहरी पृष्ठ के बीच विभवान्तर V है। यदि गोलीय खोल को अब `-3Q` आवेश दिया जाए , तो उन्ही दो पृष्ठों के बीच न्य विभवान्तर होगा
View Solutionजब हम X- अक्ष कि दिशा में `x=-1cm` से `x=+1` cm तक चलते हैं , तो विभवान्तर , 120 V से घटकर 80 V हो जाता है मूल बिंदु पर वैधुत क्षेत्र
View SolutionR (मीटर ) व्यासार्ध वाले दो एकसमान पतले रिंग , समाक्ष रुप से एक दूसरे से R दुरी पर रखे जाते हैं। यदि दोनों रिंगो पर क्रमशः `Q_(1)` और `Q_(2)` कूलॉम आवेश , एकसमान रूप से फैलाए गए हो , तो एक आवेश q को एक रिंग के केंद्र से दूसरे के केंद्र तक के जाने में किया गया कार्य है
View Solutiond मोटाई का एक परावैधुत स्लैब , किसी समांतर प्लेट संधारित्र में रखा जाता है जिसकी ऋणात्मक प्लेट x=0 पर है और धनात्मक प्लेट x=3d पर। स्लैब , दोनों प्लेटों से समान दुरी पर है। संधारित्र को कुछ आवेश दिया जाता है। ज्यों - ज्यों x,0 से 3d की ओर जाता है
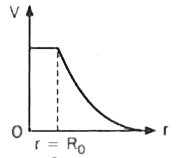
View Solutionएक गोलीय सममित आवेश समूह , मूल बिंदु पर केंद्रित है [ चित्र I.38]| जब वैधुत विभव
`V=(Q)/(4piepsilon_(0)R_(0)),rleR`
`V=(Q)/(4piepsilon_(0)r)rgtR_(0)`
हो तो
View Solutionएक समांतर - प्लेट संधारित्र , किसी निश्चित विभव तक आवेशित किया जाता है। फिर आवेशन करने वाली बैटरी अलग कर दी जाती है। अब यदि संधारित्र की प्लेटें एक दूसरे से परे की जाएँ , तो
View Solutionचित्र I.39 में दिखाए अनुसार एक सम्पूर्ण चालक के अंदर दीर्घवृत्तज कोटर बनाया जाता है। एक धनात्मक आवेश q कोटर के केंद्र पर रखा जाता है। बिंदु A और B कोटर के पृष्ठ पर है। तब
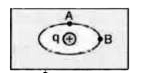
View Solutionएक समांतर - प्लेट वायु संधारित्र ,एक बैटरी से जोड़ा जाता है। संधारित्र के साथ जुडी राशियाँ आवेश , वोल्टता , वैधुत क्षेत्र और ऊर्जा , क्रमशः `Q_(0),V_(0),E_(0)` और `U_(0)` है। बैटरी से जुडी हुई प्लेटों के बीच की जगह को भरने के लिए एक परावैधुत स्लैब रखा जाता है। अब Q,V,E और U द्वारा निर्देशित संगत राशियाँ पहली राशियों से ऐसे सम्बद्ध हैं
View Solutionएक समांतर - प्लेट संधारित्र आवेशित किया जाता है और फिर आवेशन करने वाली बैटरी पृथक कर दी जाती है। यदि विधुतरोधी हैण्डलों से संधारित्र की प्लेटें एक दूसरे से और परे की जाएँ , तो
View Solutionदो ऋणात्मक आवेश (प्रत्येक आवेश =-q) , Y- अक्ष पर (0,a) और (0,-a) बिंदुओं पर स्थिर रखे जाते हैं। एक धनात्मक आवेश Q,X- अक्ष पर (2a,0) बिंदु पर स्थित अवस्था से छोड़ा जाता है। आवेश Q
View Solutionएक ताँबे के सिक्के का द्रव्यमान 3 g है और इसमें `3xx10^(22)` के परमाणु हैं। मान लें कि दो सिक्कों के इलेक्ट्रॉन का कुछ अंश नकाल लिया जाता है जिससे प्रत्येक पर एक नेट धनात्मक आवेश `+q` रह जाता है। जब एक सिक्के को मेज पर रखा जाता है , तो दूसरा इसके भार (mg) के विरुद्ध लग रहे वैधुत बल F द्वारा पहले से 2m ऊपर लटक जाता है जैसा कि चित्र I.40 में दिखाया गया है। कूलॉम नियम के अनुसार दो आवेशित बिंदुओं के बीच बल `F=9xx10^(9)(q_(1)q_(2))/(r^(2))N`, जब `q_(1)` और `q_(2)` कूलॉम में मापे जाते हैं और r, मीटर में। आवेश क्वान्टित है अर्थात q=ne जहाँ `e=1.6xx10^(-19)C` है।
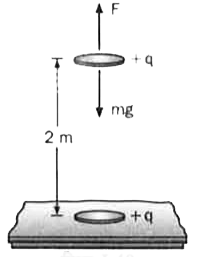
आवेश q का मान है
View Solutionएक ताँबे के सिक्के का द्रव्यमान 3 g है और इसमें `3xx10^(22)` के परमाणु हैं। मान लें कि दो सिक्कों के इलेक्ट्रॉन का कुछ अंश नकाल लिया जाता है जिससे प्रत्येक पर एक नेट धनात्मक आवेश `+q` रह जाता है। जब एक सिक्के को मेज पर रखा जाता है , तो दूसरा इसके भार (mg) के विरुद्ध लग रहे वैधुत बल F द्वारा पहले से 2m ऊपर लटक जाता है जैसा कि चित्र I.40 में दिखाया गया है। कूलॉम नियम के अनुसार दो आवेशित बिंदुओं के बीच बल `F=9xx10^(9)(q_(1)q_(2))/(r^(2))N`, जब `q_(1)` और `q_(2)` कूलॉम में मापे जाते हैं और r, मीटर में। आवेश क्वान्टित है अर्थात q=ne जहाँ `e=1.6xx10^(-19)C` है।
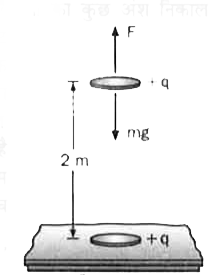
हर सिक्के से निकाले गए इलेक्ट्रॉनों कि संख्या है
View Solutionएक ताँबे के सिक्के का द्रव्यमान 3 g है और इसमें `3xx10^(22)` के परमाणु हैं। मान लें कि दो सिक्कों के इलेक्ट्रॉन का कुछ अंश नकाल लिया जाता है जिससे प्रत्येक पर एक नेट धनात्मक आवेश `+q` रह जाता है। जब एक सिक्के को मेज पर रखा जाता है , तो दूसरा इसके भार (mg) के विरुद्ध लग रहे वैधुत बल F द्वारा पहले से 2m ऊपर लटक जाता है जैसा कि चित्र I.40 में दिखाया गया है। कूलॉम नियम के अनुसार दो आवेशित बिंदुओं के बीच बल `F=9xx10^(9)(q_(1)q_(2))/(r^(2))N`, जब `q_(1)` और `q_(2)` कूलॉम में मापे जाते हैं और r, मीटर में। आवेश क्वान्टित है अर्थात q=ne जहाँ `e=1.6xx10^(-19)C` है।
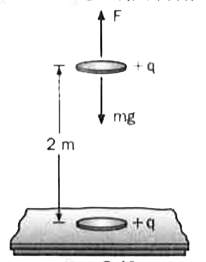
ताँबे के परमाणुओं का वह अंश जिसमें इलेक्ट्रॉन नहीं है
View Solutionकिसी एकसमान वैधुत क्षेत्र `vecE` में एक दूसरे से x दुरी पर दो बिंदुओं A और B के बीच विभवान्तर `(DeltaV)=-Ex` होता है जहाँ x, क्षेत्र रेखाओं के समांतर मापा जाता है। यदि एक आवेश `q_(0)` बिंदु A से B की ओर जाए , तो स्थितिज ऊर्जा में परिवर्तन `DeltaU=q_(0)DeltaV` होता है।
`8.0xx10^(4)V//m` परिमाण वाले किसी एकसमान वैधुत क्षेत्र में जो धनात्मक X- अक्ष की दिशा में है , एक प्रोटॉन को स्थिर अवस्था में छोड़ा जाता है। प्रोटॉन का `vecE` की दिशा में 0.50m विस्थापन होता है [ चित्र I.41] प्रोटॉन का द्रव्यमान `=1.66xx10^(-27)kg` और आवेश `=1.6xx10^(-19)C` है।
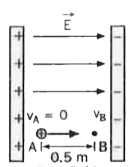
जैसे - जैसे प्रोटॉन A से B की ओर चलता है
View Solutionकिसी एकसमान वैधुत क्षेत्र `vecE` में एक दूसरे से x दुरी पर दो बिंदुओं A और B के बीच विभवान्तर `(DeltaV)=-Ex` होता है जहाँ x, क्षेत्र रेखाओं के समांतर मापा जाता है। यदि एक आवेश `q_(0)` बिंदु A से B की ओर जाए , तो स्थितिज ऊर्जा में परिवर्तन `DeltaU=q_(0)DeltaV` होता है।
`8.0xx10^(4)V//m` परिमाण वाले किसी एकसमान वैधुत क्षेत्र में जो धनात्मक X- अक्ष की दिशा में है , एक प्रोटॉन को स्थिर अवस्था में छोड़ा जाता है। प्रोटॉन का `vecE` की दिशा में 0.50m विस्थापन होता है [ चित्र I.41] प्रोटॉन का द्रव्यमान `=1.66xx10^(-27)kg` और आवेश `=1.6xx10^(-19)C` है।
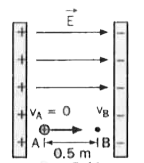
A ओर B बिंदुओं के बीच वैधुत विभव में अंतर है
View Solutionकिसी एकसमान वैधुत क्षेत्र `vecE` में एक दूसरे से x दुरी पर दो बिंदुओं A और B के बीच विभवान्तर `(DeltaV)=-Ex` होता है जहाँ x, क्षेत्र रेखाओं के समांतर मापा जाता है। यदि एक आवेश `q_(0)` बिंदु A से B की ओर जाए , तो स्थितिज ऊर्जा में परिवर्तन `DeltaU=q_(0)DeltaV` होता है।
`8.0xx10^(4)V//m` परिमाण वाले किसी एकसमान वैधुत क्षेत्र में जो धनात्मक X- अक्ष की दिशा में है , एक प्रोटॉन को स्थिर अवस्था में छोड़ा जाता है। प्रोटॉन का `vecE` की दिशा में 0.50m विस्थापन होता है [ चित्र I.41] प्रोटॉन का द्रव्यमान `=1.66xx10^(-27)kg` और आवेश `=1.6xx10^(-19)C` है।
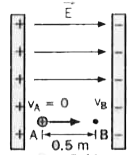
A बिंदु से B तक विस्थापन में प्रोटॉन की वैधुत स्थितिज ऊर्जा में अंतर है
View Solutionकिसी एकसमान वैधुत क्षेत्र `vecE` में एक दूसरे से x दुरी पर दो बिंदुओं A और B के बीच विभवान्तर `(DeltaV)=-Ex` होता है जहाँ x, क्षेत्र रेखाओं के समांतर मापा जाता है। यदि एक आवेश `q_(0)` बिंदु A से B की ओर जाए , तो स्थितिज ऊर्जा में परिवर्तन `DeltaU=q_(0)DeltaV` होता है।
`8.0xx10^(4)V//m` परिमाण वाले किसी एकसमान वैधुत क्षेत्र में जो धनात्मक X- अक्ष की दिशा में है , एक प्रोटॉन को स्थिर अवस्था में छोड़ा जाता है। प्रोटॉन का `vecE` की दिशा में 0.50m विस्थापन होता है [ चित्र I.41] प्रोटॉन का द्रव्यमान `=1.66xx10^(-27)kg` और आवेश `=1.6xx10^(-19)C` है।
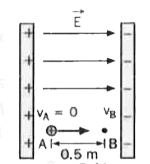
स्थिर अवस्था से चलकर 0.50m तय करने के बाद प्रोटॉन की गति `v_(B)` है
View Solutionq आवेश और A क्षेत्रफल वाली आवेश की एक समतल चादर का वैधुत क्षेत्र `E-(q)/(2epsilon_(0)A)` है। समान्य संकेतन से , एक समांतर - प्लेट संधारित्र में
`E=(q)/(epsilon_(0)A),V=(qd)/(epsilon_(0)A)` और `C=(epsilon_(0)A)/(d)`
आइए अब हम मान लें कि एक समांतर - प्लेट संधारित्र कि दोनों प्लेटों A और B को दिए गए आवेश अलग - अलग हैं , अर्थात `q_(1)` और `q_(2)` जैसा कि चित्र I.42 में दिखाया गया हैं |
प्लेट A के a और b पृष्ठों पर आवेश हैं
View Solutionq आवेश और A क्षेत्रफल वाली आवेश की एक समतल चादर का वैधुत क्षेत्र `E-(q)/(2epsilon_(0)A)` है। समान्य संकेतन से , एक समांतर - प्लेट संधारित्र में
`E=(q)/(epsilon_(0)A),V=(qd)/(epsilon_(0)A)` और `C=(epsilon_(0)A)/(d)`
आइए अब हम मान लें कि एक समांतर - प्लेट संधारित्र कि दोनों प्लेटों A और B को दिए गए आवेश अलग - अलग हैं , अर्थात `q_(1)` और `q_(2)` जैसा कि चित्र I.42 में दिखाया गया हैं |
प्लेट B के c और d पृष्ठों पर आवेशों हैं
View Solutionq आवेश और A क्षेत्रफल वाली आवेश की एक समतल चादर का वैधुत क्षेत्र `E-(q)/(2epsilon_(0)A)` है। समान्य संकेतन से , एक समांतर - प्लेट संधारित्र में
`E=(q)/(epsilon_(0)A),V=(qd)/(epsilon_(0)A)` और `C=(epsilon_(0)A)/(d)`
आइए अब हम मान लें कि एक समांतर - प्लेट संधारित्र कि दोनों प्लेटों A और B को दिए गए आवेश अलग - अलग हैं , अर्थात `q_(1)` और `q_(2)` जैसा कि चित्र I.42 में दिखाया गया हैं |
दोनों प्लेटों A और B के बीच वैधुत क्षेत्र हैं
View Solutionq आवेश और A क्षेत्रफल वाली आवेश की एक समतल चादर का वैधुत क्षेत्र `E-(q)/(2epsilon_(0)A)` है। समान्य संकेतन से , एक समांतर - प्लेट संधारित्र में
`E=(q)/(epsilon_(0)A),V=(qd)/(epsilon_(0)A)` और `C=(epsilon_(0)A)/(d)`
आइए अब हम मान लें कि एक समांतर - प्लेट संधारित्र कि दोनों प्लेटों A और B को दिए गए आवेश अलग - अलग हैं , अर्थात `q_(1)` और `q_(2)` जैसा कि चित्र I.42 में दिखाया गया हैं |
दोनों प्लेटों A और B के बीच विभवान्तर है
View Solutionq आवेश और A क्षेत्रफल वाली आवेश की एक समतल चादर का वैधुत क्षेत्र `E=(q)/(2epsilon_(0)A)` है। समान्य संकेतन से , एक समांतर - प्लेट संधारित्र में
`E=(q)/(epsilon_(0)A),V=(qd)/(epsilon_(0)A)` और `C=(epsilon_(0)A)/(d)`
आइए अब हम मान लें कि एक समांतर - प्लेट संधारित्र कि दोनों प्लेटों A और B को दिए गए आवेश अलग - अलग हैं , अर्थात `q_(1)` और `q_(2)`
तो संधारित्र कि धारिता है -
View Solutionनाभिक आवेश (Ze) ,R व्यासार्ध में नाभिक के अंदर आसमान रूप से वितरित है। आवेश घनत्व `rho(r )` (प्रति इकाई आयतन आवेश ), चित्र I.43 में दिखाए अनुसार केवल नाभिक के केंद्र से त्रिज्या दूरी r पर निर्भर है। वैधुत क्षेत्र केवल त्रिज्या दिशा में है।
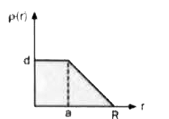
`r=R` पर वैधुत क्षेत्र
View Solutionनाभिक आवेश (Ze) ,R व्यासार्ध में नाभिक के अंदर आसमान रूप से वितरित है। आवेश घनत्व `rho(r )` (प्रति इकाई आयतन आवेश ), चित्र I.43 में दिखाए अनुसार केवल नाभिक के केंद्र से त्रिज्या दूरी r पर निर्भर है। वैधुत क्षेत्र केवल त्रिज्या दिशा में है।
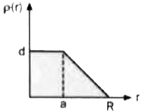
a=0 के लिए d (चित्र में दिखाए अनुसार P का अधिकतम मान ) का मान है
View Solutionनाभिक आवेश (Ze) ,R व्यासार्ध में नाभिक के अंदर आसमान रूप से वितरित है। आवेश घनत्व `rho(r )` (प्रति इकाई आयतन आवेश ), चित्र I.43 में दिखाए अनुसार केवल नाभिक के केंद्र से त्रिज्या दूरी r पर निर्भर है। वैधुत क्षेत्र केवल त्रिज्या दिशा में है।
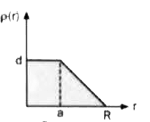
नाभिक के अंदर वैधुत क्षेत्र , आम तौर पर r पर रेखीय रूप से निर्भर देखा जाता है। इसका अर्थ है
View Solution
प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प questions and complete solutions for chapter धारिता और परावैधुत पदार्थ of GRB PUBLICATIONS PHYSICS (HINDI) of Class 12
All Exercises from GRB PUBLICATION HINDI Class 12 PHYSICS धारिता और परावैधुत पदार्थ
- NCERT पाठ्यपुस्तक अभ्यास : उत्तरों सहित
- उच्चस्तरीय चिंतन : प्रश्नोत्तरी
- उदाहरण
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (कथन - कारण - आधारित प्रश्न)
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (कॉलम मिलाना)
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (रिक्त स्थान भरना )
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (सत्य या असत्य )
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक सही विकल्प)
- प्रतिरुपी अभ्यास
- प्रश्नोत्तरी : 1 अंक
- प्रश्नोत्तरी : 2 अंक और 3 अंक
- प्रश्नोत्तरी : 5 अंक
- विषय - आधारित अभ्यास (धारिता)
- विषय - आधारित अभ्यास (संधारित्र का संयोजन )
- विषय - आधारित अभ्यास (संधारित्र में संचित ऊर्जा )
- विषय - आधारित समस्याएँ : ( धारिता )
- विषय - आधारित समस्याएँ : ( विविध प्रश्न )
- विषय - आधारित समस्याएँ : ( संधारित्र में संचित ऊर्जा )
- विषय - आधारित समस्याएँ : ( संधारित्रों का संयोजन )