Complete Solutions to प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक सही विकल्प) of chapter धारिता और परावैधुत पदार्थ of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | धारिता और परावैधुत पदार्थ |
| GRB PUBLICATION HINDI | प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक सही विकल्प) |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
चालक पेंट से कोट कि हुई एक टेबल - टेनिस की गेंद एक रेशमी धागे से लटकाई जाती है ताकि यह दो धातु की प्लेटों के बीच लटके। एक प्लेट को भूसंपर्कित किया जाता है। जबकि दूसरी एक उच्च वोल्टता जनित्र से जोड़ी जाती है। गेंद
View Solutionसमान व्यासार्ध और समान आवेश वाले दो गोलाकर चालक B और C जब एक दूसरे से कुछ दुरी पर रखे जाते हैं तो वे एक दूसरे को F बल से प्रतिकर्षित करते हैं। B के बराबर व्यासार्थ वाले परन्तु अनावेशित एक तीसरे गोलाकार चालक A को चालक B के साथ छुआकर फिर C के साथ छुआया जाता है और अंत में दोनों से परे ले जाया जाता है। B और C के बीच नया प्रतिकर्षण बल है
View Solutionदो अनावेशित गेंदें एक - दूसरे को कुछ बल के साथ आकर्षित करती हैं। यदि उन्हें एक दूसरे से छुआकर फिर उतनी ही दूर अलग कर दिता जाए , तो दोनों गेंदें
View Solutionयदि दो समान आवेशों Q और Q को जोड़ने वाली रेखा के केंद्र पर , एक आवेश q ऐसे रख दिया जाए कि समूह साम्यावस्था में हों , तो Q का मान है
View Solutionएक आवेश Q के पहले दो टुकड़े q और q किए जाते हैं। बाद में ये आवेश q और q कुछ दुरी पर रख दिए जाते हैं। यदि दोनों आवेशों के बीच आकर्षण का बल अधिकतम हो , तो
View Solutionचार आवेश (प्रत्येक आवेश =-Q) एक वर्ग के चार कोनो पर रख दिए जाते हैं और एक आवेश q इसके केंद्र पर। यदि समूह साम्यावस्था में है , तो Q का मान है :
View Solutionएक धनात्मक आवेशित काँच कि छड़ एक वस्तु को आकर्षित करती है। वस्तु अवश्य ही होनी चाहिए
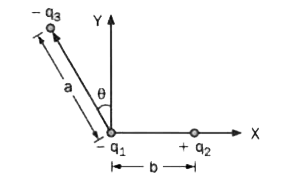
View Solutionतीन आवेश `(-q1),(+q_(2))` और `(-q_(3))` चित्र I.1 में दिखाए अनुसार रखे जाते हैं। आवेश `(-q_(1))` बल पर का x- घटक इनके अनुपाती है
View Solutionएक वर्ग के दो विपरीत कोनो पर आवेश Q रखे जाते हैं। दूसरे दो कोनो पर आवेश (-q) रखे जाते हैं। यदि Q पर नेट वैधुत बल शून्य हो , तो `Q//q` इनके बराबर है
View SolutionA और B दो एकसमान गोलाकार आवेशित वस्तुएँ हैं जो एक दूसरे से कुछ दुरी पर रखी जाने पर एक दूसरे को F बल से प्रतिकर्षित करती हैं। उसी आकर का एक तीसरा अनावेशित गोला , B के सम्पर्क में लाया जाता है फिर दूर हटा लिया जाता है। इसे फिर A और B मध्य - बिंदु पर रखा जाता है C पर बल का परिणाम है
View Solutionएक आवेश Q के दो भाग q और Q-q किए जाते हैं। उनके बीच अधिकतम बल के लिए q का क्या मान है ?
View Solutionदो समांतर आवेश एक दूसरे से d दूरी पर है। इसके अभिलम्ब द्विभाजक पर केंद्र से x दूरी पर रखा एक तीसरा आवेश अधिकतम कूलॉम बल अनुभव करेगा जब
View Solutionनिम्न में गलत कथन ढूँढे। कूलॉम नियम ने ठीक उसे वैधुत बल वर्णित किया जो
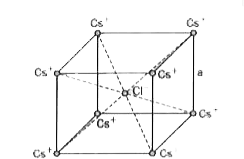
View Solutionमूल (basic) CsCl क्रिस्टल कि बनावट में `Cs^(+)` और `Cl^(-)` आयन चित्र I.2 में दिखाए अनुसार bcc व्यवस्था में पड़े होते हैं। आठ `Cs^(+)` आयनो द्वारा `Cl^(-)` आयन पर लगाया गया स्थिरवैधुत बल है
View Solution1 से 5 नम्बरों वाली पाँच गेंदें अलग - अलग धागों से लटकाई जाती हैं। जोड़ो (1,2),(2,4) और (4,1) में स्थिरवैधुत आकर्षण दिखता है तथा जोड़ों (2,3) और (4,5) में प्रतिकर्षण। इसलिए गेंद 1 अवश्य ही होनी चाहिए
View Solutionएक दूसरे से d दूरी पर दो आवेशित गोले , एक दूसरे पर कुछ बल F लगाते हैं। यदि वे परावैधुतांक 2 वाले किसी द्रव में डुबो दिए जाएँ , तो बाकी सभी शर्ते वही रहने पर उन द्वारा लगाया गया बल कितना होगा ?
View Solutionतीन आवेश +4q,Q और q ,l लम्बाई वाली सीधी रेखा में क्रमशः `0,l//2` और l दूरियों वाले बिंदुओं पर रखे जाते हैं। Q कितना होना चाहिए कि आवेश Q पर नेट बल शून्य हो ?
View Solutionएक इलेक्ट्रॉन , एक हाइड्रोजन परमाणु के नाभिक के चारों ओर r व्यासार्ध कि वृत्ताकार कक्षा में घूम रहा है। दोनों के बीच कूलॉम बल `vecF` है
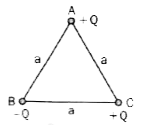
View Solutionतीन आवेश , a भुजा वाली एक समबाहु त्रिभुज के कोनों पर चित्र I.3 के अनुसार रखे जाता हैं। कोने A पर रखे आवेश द्वारा BC पर लम्बवत दिशा में अनुभव किया गया बल है
View Solutionकूलॉम बल को सक्रिय होने के लिए परमाणु का कम से कम साइज होगा
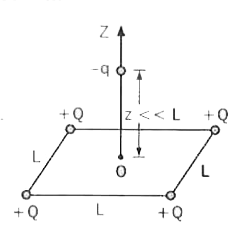
View Solutionचित्र I.4 में दिखाए एक कठोर वर्गाकार ढाँचे के चारों कोनों पर एक ही परिमाण Q के चार बिंदु धनात्मक आवेश रखे जाते हैं। ढाँचे का तल , Z - अक्ष पर लम्बवत है। यदि एक ऋणात्मक बिंदु आवेश , ढाँचे से z दूरी पर रख दिया जाए , तो
View Solutionएकसमान परिमाण के दो आवेश r दुरी पर एक दूसरे पर F बल लगाते हैं। यदि आवेश आधे कर दिए जाएँ और उनके बीच की दुरी दुगुनी कर दी जाए , तो हर आवेश पर लगने वाला नया बल है
View Solution`1muC` के अनन्त आवेश , X - अक्ष पर x=1,2,4,8,…, `oo` निर्देशांकों पर रखे जाते हैं। यदि मूल बिंदु पर आवेश 1 C रखा जाए , तो इस आवेश पर कितना नेट बल लगेगा ?
View Solutionबिंदु आवेश ,`+4q,-q` और `+4q,X`- अक्ष पर क्रमशः `x=0,x=a` और x=2a बिंदुओं पर रखे जाते हैं।
View Solutionसमान मात्रा q के तीन धनात्मक आवेश एक समबाहु त्रिभुज के कोनों पर रखे जाते हैं। परिणामी क्षेत्र रेखाएँ इस प्रकार खींची जानी चाहिएँ
View Solutionएक आवेशित तेल की बूँद , `3xx10^(4)V//m` के एकसमान क्षेत्र में लटकाई जाती हैं ताकि न यह गिरे और न ही ऊपर चढ़े। बूँद का आवेश होगा
(बूँद का भार `=9.9xx10^(-15_kg` और `g=10m//s^(2))`
View Solutionएक धातु के खोखले गोले के अंदर के कोटर में आवेश q रखा है। निम्न चित्रों में से कौन -सा चित्र , वैधुत बल रेखाओं को सही रूप से प्रदर्शित करता है ?
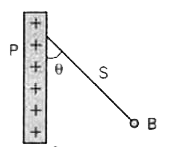
View Solutionएक आवेशित गेंद B , रेशमी धागे S से लटकी हुई है जो चित्र I.5 में दिखाए अनुसार एक बड़ी आवेशित चालक चादर P के साथ `theta` कोण बनाती है। चादर का पृष्ठीय घनत्व इनके समानुपाती है
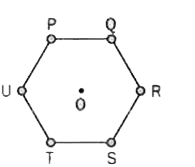
View Solutionएक ही मात्रा के छः आवेश , तीन धनात्मक और तीन ऋणात्मक , एक सम - षट्भुज के कोनों पर रखे जाते हैं [ चित्र I.6] ताकि बिंदु O पर वैधुत क्षेत्र , उस वैधुत क्षेत्र का दोगुना हो जब केवल R पर रखा जाए। क्रमशः P,Q,R,ST और U पर निम्न में से आवेशों का कौन - सा संयोजन अनुमेय है ?
View Solutionp आघूर्ण का एक वैधुत द्विध्रुव , वैधुत क्षेत्र E की बल रेखाओं के अनुदिश रखा जाता है और यह साम्यावस्था में है। इसे `180^(@)` के कोण से विक्षेपित करने के लिए किया गया कार्य होगा
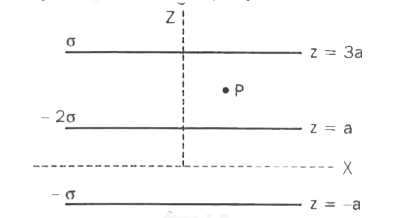
View Solutionतीन अनन्त लम्बाई वाली आवेश की चादरें , चित्र I.7 के अनुसार रखी जाती हैं। बिंदु P पर वैधुत क्षेत्र है
View Solutionदो बिंदु आवेश +8q और -2q , क्रमशः x=0 और x=L पर रखे हुए हैं। X- अक्ष पर वह बिंदु , जहाँ पर इन दोनों बिंदु आवेशों के कारण नेट वैधुत क्षेत्र शून्य है , इस स्थान पर है
View Solution`r_(A)` और `(r_(B)gtr_(A))`व्यासार्ध वाले दो सकेंद्री चालक पतले गोलीय खोल A और B , आवेश `Q_(A)` और `(-Q_(B))(|Q_(B)|gt|Q_(A)|)` तक आवेशित किए जाते हैं। केंद्र से गुज़रती रेखा पर वैधुत क्षेत्र का सही चित्रण है
View Solutionएक वैधुत द्विध्रुव , किसी एकसमान वैधुत क्षेत्र के साथ `30^(@)` के कोण पर रखा जाता है। द्विध्रुव अनुभव करेगा
View Solutionधातु के विधुतरोधी गोलीय खोल के केंद्र पर एक बिंदु आवेश रखा जाता है। तब
View Solutionएक सरल लोलक की लम्बाई l है और इसके गोलक का द्रव्यमान m है। गोलक को Q कूलॉम आवेश दिया जाता है। लोलक को एक आवेशित समान्तर - प्लेट संधारित्र की ऊर्ध्वाधर प्लेटों के बीच लटकाया जाता है। यदि प्लेटों के बीच वैधुत क्षेत्र की तीव्रता E हो , तो लोलक का आवर्तकाल है
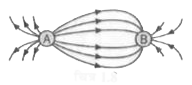
View Solutionचित्र I.8 में दो आवेशों A और B के कारण वैधुत क्षेत्र का आकाशीय वितरण दिखाया गया है। निम्न में से कौन -सा कथन सत्य है ?
View Solutionमान लें एक द्विध्रुव का वैधुत क्षेत्र , इसके अक्षीय तल में l दुरी पर `E_(a)` है और निरक्षीय तल में l दुरी पर `E_(q)` है। `E_(a)` और `E_(q)` के बीच सम्बन्ध है
View Solutionदो बिंदु आवेश (Q) और `(-2Q)` आपस में कुछ दुरी पर पड़े हैं। यदि (Q) के स्थान पर वैधुत क्षेत्र E हो , तो (-2Q) के स्थान पर वैधुत क्षेत्र होगा
View SolutionR व्यासार्ध के किसी एकसमान आवेशित कुचालक गोले का वैधुत क्षेत्र , इसके केंद्र से दुरी के फंक्शन के रूप में ग्राफ से ऐसे प्रदर्शित किया जाता है
View Solution3e परिमाण के आवेश और 2m द्रव्यमान वाला एक आवेश , वैधुत क्षेत्र `vecE` में चल रहा है। आवेश को दिया गया त्वरण है
View Solutionएक असमान वैधुत क्षेत्र में रखा हुआ वैधुत द्विध्रुव अनुभव करता है
View Solutiona व्यासार्ध की एक अर्द्धवृत्ताकार चाप , एकसमान रूप से आवेशित की जाती है। प्रति यूनिट लम्बाई आवेश , `lambda` है। केंद्र पर वैधुत क्षेत्र है
View SolutionR व्यासार्ध का एक ठोस गोला , एकसमान रूप से आवेशित किया जाता है ताकि इसका आयतन आवेश घनत्व `rho` हो। `r(rltR)` दुरी पर वैधुत क्षेत्र है
View Solutionएक द्विध्रुव वैधुत क्षेत्र के समान्तर रखा जाता है। यदि द्विध्रुव को `60^(@)` के कोण से घुमाने पर W कार्य करना पड़े तो इसे `180^(@)` के कोण से घुमाने में किया गया कार्य है
View Solutionचित्र I.9 में दिखाया आवेश समूह और एक गोलाकार गाउसीय पृष्ठ लें। गोलाकार पृष्ठ पर वैधुत क्षेत्र का फ्लक्स निकालते हुए , वैधुत क्षेत्र इनके कारण होगा
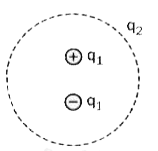
View Solutionमान लें R व्यासार्ध और कुल Q आवेश वाले एक ठोस गोले का आवेश घनत्व वितरण `rho(r)=(Q)/(piR^(4))r` है। गोले के केंद्र से `r_(1)` दुरी पर गोले के अंदर बिंदु P पर वैधुत क्षेत्र का परिणाम है
View Solutionयदि किसी बंद पृष्ठ में प्रवेश करने वाले और इससे निकलने वाले फ्लक्स के परिणाम क्रमश :`phi_(1)` और `phi_(2)` हों तो समूह के अंदर वैधुत क्षेत्र होगा
View Solutionगाउस नियम के अनुसार एक अनन्त लम्बी सीधी तार का वैधुत क्षेत्र इनके अनुपाती है
View Solutionएक गोले के अंदर एक वैधुत द्विध्रुव है। गोले के आर -पार कुल फ्लक्स है
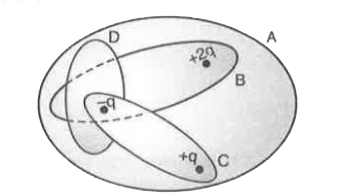
View Solutionचार गाउसीय पृष्ठों A,B,C और D में चित्र I.10 में दर्शाए अनुसार आवेश हैं। सबसे अधिक ऋणात्मक से आरम्भ करते हुए इन पृष्ठों के बढ़ते हुए वैधुत फ्लक्स के क्रम में निम्न अनुसार श्रेणीबद्ध किया जा सकता है
View Solutionएक घन के केंद्र पर आवेश Q रखा जाता है इसके एक फलक से गुजरने वाला फ्लक्स कितना है ?
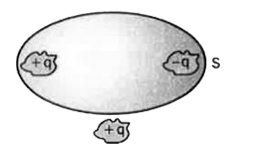
View Solutionचित्र में आवेशों का वितरण दिखाया गया है। इन आवेशों के वैधुत क्षेत्र का पृष्ठ S से गुजरने वाला फ्लक्स है
View SolutionR व्यासार्ध और L लम्बाई का एक बेलन , किसी एकसमान वैधुत क्षेत्र E में रखा जाता है जो बेलन के अक्ष के समान्तर है। बेलन के पृष्ठ से गुजरने वाला कुल फलक्स है
View Solutionक्रमशः `(+sigma)` और `(-sigma)` आवेश घनत्व वाली दो अनन्त लम्बी समान्तर चालक प्लेटें , एक दूसरे से थोड़ी दुरी पर हैं। दोनों प्लेटों के बीच माध्यम निर्वात है। यदि निर्वात की परावैधुत विधुतशीलता `epsilon_(0)` हो , तो प्लेटों के बीच के स्थान में वैधुत क्षेत्र है
View SolutionL मीटर भुजा वाला एक वर्गाकार पृष्ठ , पृष्ठ के तल में है [ चित्र I.12]| पृष्ठ के तल में ही एकसमान वैधुत क्षेत्र `vecE` , चित्र में दिखाए अनुसार वर्गाकार पृष्ठ के केवल नीचे वाले आधे भाग में हैं। पृष्ठ के साथ सम्बद्ध वैधुत फ्लक्स (SI यूनिट में ) है

View Solutionव्यासार्ध R वाला एक गोला , एकसमान वैधुत क्षेत्र E में रखा जाता है। गोले के पृष्ठ के ऊपर कुल वैधुत फ्लक्स है
View Solutionएक आवेश Q , एक घन के केंद्र पर रखा जाता है। घन के सभी छः फलकों में से गुजरने वाला वैधुत फ्लक्स है
View Solutionदो बड़ी समान्तर पतली धातु चादरों पर विपरीत आवेशों के समान पृष्ठीय आवेश घनत्व `2.56xx10^(-11)C//m^(2)` हैं। इन चादरों के बीच वैधुत क्षेत्र है
View Solutiona भुजा वाले एक घन के एक किनारे पर एक वैधुत आवेश Q रखा जाता है। इसके एक फलक से गुजरने वाला वैधुत फ्लक्स होगा
View Solutionएक आवेश Q एक घन के केंद्र पर स्थित है। किसी भी फलक से गुजरने वाला वैधुत फ्लक्स है
View Solutionएक खोखले बेलन के अंदर आवेश Q कूलॉम है [ चित्र I.13] |यदि वक्र पृष्ठ B से सम्बद्ध फ्लक्स (वोल्ट मीटर इकाई में )`phi` (वोल्ट मीटर इकाई में ) होगा

View Solutionदो बिंदु P और Q क्रमशः 10 V और -4V के विभवों पर रखे जाते हैं। बिंदु P से Q तक 100 इलेक्ट्रॉनों को ले जाने में किया गया कार्य है
View Solutionइस प्रश्न में कथन - 1 और कथन - 2 हैं। कथनों के बाद दिए गए चार विकल्पों में से वह विकल्प ढूंढे जो दोनों कथनों का सही वर्णन करता है।
कथन - 1 : बिंदु P से बिंदु Q तक जा रहे एक आवेशित कण पर किसी स्थिरवैधूत क्षेत्र द्वारा किया गया नेट कार्य , बिंदु P को बिंदु Q से जोड़ने वाले पर निर्भर नहीं है।
कथन - 2 : एक संरक्षी बल द्वारा , वस्तु को एक बंद लूप के अनुदिश चलाने में किया गया नेट कार्य शून्य है।
View Solutionकिसी स्थान पर धनात्मक X दिशा की ओर मुँह किया हुआ एकसमान वैधुत क्षेत्र है। मान के लें कि A मूल बिंदु है , B(X - अक्ष पर `x=+1cm पर ) एक बिंदु और C(Y - अक्ष पर y=+1cm पर ) एक अन्य बिंदु है। तब बिंदुओं A,B और C पर विभवों को ये शर्ते पूरी चाहिएँ
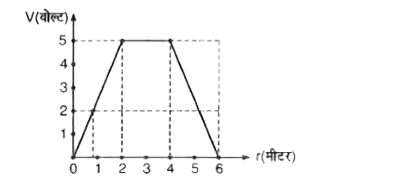
View Solutionविभव V का एक निश्चित बिंदु से r दुरी के साथ परिवर्तन चित्र I.14 में दिखाया गया गया है। r=5m पर वैधुत क्षेत्र है
View Solutionदो समान आवेश , X - अक्ष पर x=-a और x=+a पर स्थित है। एक और बिंदु आवेश Q मूल बिंदु पर पड़ा है। जब आवेश Q को X - अक्ष के अनुदिश एक थोड़ी दुरी x तक विस्थापित किया जाता है , तो इसकी वैधुत स्थितिज ऊर्जा में परिवर्तन लगभग इनके अनुपाती है
View Solutionधनात्मक आवेश घनत्व `sigma` वाली एक अनन्त चादर से Z लम्बवत दुरी पर वैधुत विभव है
View SolutionR व्यासार्ध वाले दो पतले तार के रिंग , जिनके अक्ष संपाती है , एक दूसरे से d दुरी पर रखे जाते हैं। दोनों रिंगो पर आवेश (+q) और (-q) हैं। दोनों रिंगो के केन्द्रो के बीच विभवान्तर है
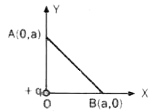
View Solutionतीन आवेश Q,+q और +q एक समकोण समद्विबाहु त्रिभुज के कोनों पर चित्र I.15 में दिखाए अनुसार रखे जाते है। समूह कि नेट स्थिरवैधुत ऊर्जा शून्य होगी आवेश Q , इनके बराबर हो
View Solution1 mm और 2 mm व्यासार्ध वाले दो दो गोलाकार चालक A और B एक दूसरे से 5cm कि दुरी पर हैं और एकसमान आवेशित है। यदि गोलों का एक तार से जोड़ दिया जाए , तो साम्यावस्था में चालकों A और B के पृष्ठों पर वैधुत क्षेत्रों के परिमाणों का अनुपात है
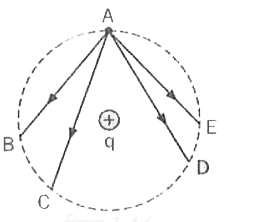
View Solutionएक बिंदु आवेश के वैधुत क्षेत्र में एक आवेश , बिंदु A से B,C,D और E तक ले जाया जाता है। किया गया कार्य [ देखे चित्र I.16]
View Solutionएक आवेशित कण Q , एक दूसरे आवेशित कण O , जो d दुरी पर स्थित है की ओर v गति से फेंका जाता है। यह निकटतम दुरी r तक जाता है और फिर वापिस लौटता है [ चित्र I.17]| यदि q को गति 2v दी जाए , तो उपगमन की निकटतम दुरी होगी

View SolutionR व्यासार्ध के एक पतले चालक गोलीय खोल पर आवेश Q है। एक और आवेश Q गोलीय खोल के केंद्र पर रख बिंदु P पर स्थिरवैधुत विभव है
View Solutionचित्र I.18 में दिखाए गए एक बिंदु आवेश Q के वैधुत क्षेत्र में एक आवेश Q को A से B तक और A से C तक ले जाया जाता है।

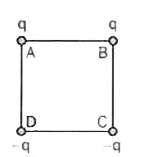
View Solutionचित्र I.19 के अनुसार एक वर्ग के कोनों पर आवेश रखे जाते है। मान ले कि केंद्र पर वैधुत क्षेत्र , `vecE` और विभव , V है। यदि बिंदुओं A और B पर आवेश क्रमशः बिंदुओं D और C पर आवेशों के साथ बदल दिए जाएँ , तो
View Solutionद्विविमीय निर्देशांक पद्धति में दो बिंदु आवेश -2q और q , बिंदुओं (-3a,0) और (+3a,0) पर रखे गए है। शून्य विभव वाले बिंदुओं का बिन्दुपथ एक वृत्त है जिसका व्यासार्ध है
View Solutionदो आवेश `q_(1)` और `q_(2)` एक दूसरे से 30 cm दूर हैं जैसा कि चित्र I.20 में दिखाया गया है। एक तीसरे आवेश `q_(3)` को 40 cm व्यासार्थ के व्रत कि त्रिज्या के अनुदिश C से D तक चलाया जाता है। समूह कि स्थितिज ऊर्जा में परिवर्तन `(q_(3))/(4piepsilon_(0))`k है , जहाँ k है

View SolutionX -अक्ष पर स्थित कुछ आवेशों के कारण किसी बिंदु `x(mum)` में पर विभव निम्न समीकरण के अनुसार है
`V(x)=(20)/((x^(2)-4))` Volt
`x=4mum` पर वैधुत क्षेत्र E है :
View Solution3 R आंतरिक व्यासार्ध और 5R बाहरी व्यासार्ध वाले एक चालक गोलीय खोल के अंदर केंद्र से R दुरी पर एक बिंदु आवेश Q रखा जाता है। गोलीय खोल के केंद्र पर विभव है
View SolutionX-Y निर्देशांक पद्धति के मूल बिंदु (0,0) पर `10^(-3)muC` का एक वैधुत आवेश रखा जाता है। दो बिंदु A और B के बीच विभवान्तर होगा
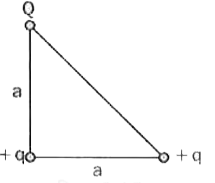
View Solutionमूल बिंदु O पर एक बिंदु आवेश +q रखा जाता है जैसा चित्र I.21 में दिखाया गया है। एक दूसरे बिंदु आवेश (-Q) को एक बिंदु A(0,a) से एक दूसरे बिंदु B (a,0) तक सीधे पथ AB के अनुदिश ले जाने में किया कार्य है
View Solutionआवेश (+q) और (-q) , क्रमशः A और B बिंदुओं , जो एक दूसरे से 2L दुरी पर है , पर रखे जाते हैं और बिंदु C,A और B बिंदुओं के बीच मध्य - बिंदु है [ चित्र I.22]| एक आवेश (+Q) को अर्धवृत CRD के अनुदिश ले जाने में किया गया कार्य है
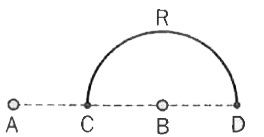
View Solutionएक आवेशित धातु के गोले में विभव V , केंद्र से दुरी R के साथ ऐसे परिवर्तित होता है
View Solutionनिम्न में से कौन -सा चित्र , स्थिर अवस्था से आरम्भ होकर V विभवान्तर से गुज़रता हुए इलेक्ट्रॉन द्वारा प्राप्त किए गए वेग v को प्रदर्शित है ?
View Solutionएक ही आकर कि n छोटी धातु कि बुँदे V वोल्ट तक आवेशित कि जाती है। यदि ये मिलकर एक अकेली बड़ी बूँद बनाएँ , तो इसका विभव होगा
View Solutionb भुजा वाले एक घन के हर कोने पर एक जैसे आवेश (-q) रखे जाते हैं। फिर घन के केंद्र पर रखे आवेश (+q) की स्थिरवैधुत स्थितिज ऊर्जा होगी
View Solutionनगण्य मोटाई की एक धातु की पन्नी , एक संधारित्र की दो प्लेटों के बीच केंद्र में रख दी जाती है। संधारित्र की धारिता होगी
View SolutionC धारिता वाले तीन एक जैसे संधारित्र श्रेणीक्रम में जोड़े जाते हैं और यह संयोजन एक और वैसे ही संधारित्र से समान्तर क्रम में जोड़ दिया जाता है। सारे संयोजन की धारिता है
View Solutionकिसी डिफीब्रिलेटर में एक `40muF` का संधारित्र , 3000 V तक आवेशित किया जाता है। संधारित्र में संचित ऊर्जा , 2 ms की अवधि के स्पंद के दौरान एक रोगी में भेजी जाती है। रोगी को दी गई शक्ति है
View Solutionदो एक जैसे धातु की प्लेटों को धनात्मक आवेश , क्रमशः `q_(1)` और `q_(2)(ltq_(1))` दिए जाते हैं। यदि उन दोनों को अब एक दूसरे के पास लाकर C धारिता वाला एक समान्तर - प्लेट संधारित्र बनाया जाए , तो उनके बीच विभवान्तर है
View SolutionA प्लेट - क्षेत्रफल और प्लेटों के बीच d दुरी वाला एक समान्तर - प्लेट संधारित्र , चित्र I.23 में दिखाए अनुसार परवैधूतों से भर दिया जाता है। परावैधुतांक `K_(1)` और `K_(2)` है। नेट धारिता है

View Solutionचित्र में दिखाई व्यवस्था की तुल्य धारिता क्या है , यदि प्लेट का क्षेत्रफल A हो ?

View Solutionएक समान्तर - प्लेट संधारित्र जिसकी प्रत्येक प्लेट का क्षेत्रफल A , उनके बीच की दुरी d और धारिता C है , `K_(1),K_(2)` और `K_(3)` परावैधुतांको वाले तीन अलग - अलग परावैधुत पदार्थों से भरा हुआ है जैसा कि चित्र I.25 में दिखाया गया है। यदि एक अकेला परावैधुत पदार्थ , इस संधारित्र में उतनी ही धारिता प्राप्त करने के लिए प्रयुक्त किया जाए , तो इसके परावैधुतांक K के लिए समीकरण होगा

View Solutionदो संधारित्र `C_(1)` और `C_(2)` क्रमशः 120V और 200V तक आवेशित किए जाते है। यह पाया जाता है कि उन्हें जोड़ने से प्रत्येक का विभव शून्य किया जा सकता है। तब
View Solutionचित्र I.26 में A और B बिंदुओं के बीच तुल्य धारिता है
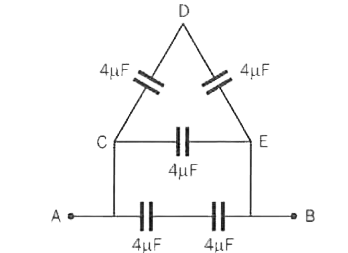
View Solutionदो एकसमान संधारित्र , समान्तर क्रम के जोड़कर V विभव तक आवेशित करके अलग किए जाते है और फिर श्रेणीक्रम में जोड़े जाते हैं अर्थात एक की धनात्मक प्लेट दूसरे की ऋणात्मक से जोड़ी जाती है
View Solutionएक समान्तर - प्लेट वायु संधारित्र की धारिता C है। जब इसे 5 परावैधुतांक वाले एक परावैधुत से आधा भर दिया जाता है , तो धारिता में प्रतिशत वृद्धि होगी
View Solutionसमान्तर क्रम में जोड़कर हर एक के सिरों पर 250 V विभवान्तर से 1.0 C आवेश संचित करने के लिए `1.0muF` के कितने संधारित्र आवश्यक है ?
View SolutionC धारिता वाले पाँच संधारित्र , चित्र I.27 के अनुसार जोड़े गए है। P और R बिंदुओं के बीच धारिता का P और Q बिंदुओं के बीच धारिता के साथ अनुपात है
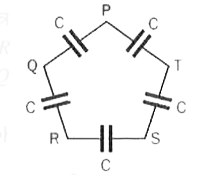
View Solution
प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक सही विकल्प) questions and complete solutions for chapter धारिता और परावैधुत पदार्थ of GRB PUBLICATIONS PHYSICS (HINDI) of Class 12
All Exercises from GRB PUBLICATION HINDI Class 12 PHYSICS धारिता और परावैधुत पदार्थ
- NCERT पाठ्यपुस्तक अभ्यास : उत्तरों सहित
- उच्चस्तरीय चिंतन : प्रश्नोत्तरी
- उदाहरण
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (कथन - कारण - आधारित प्रश्न)
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (कॉलम मिलाना)
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (रिक्त स्थान भरना )
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (सत्य या असत्य )
- प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक सही विकल्प)
- प्रतिरुपी अभ्यास
- प्रश्नोत्तरी : 1 अंक
- प्रश्नोत्तरी : 2 अंक और 3 अंक
- प्रश्नोत्तरी : 5 अंक
- विषय - आधारित अभ्यास (धारिता)
- विषय - आधारित अभ्यास (संधारित्र का संयोजन )
- विषय - आधारित अभ्यास (संधारित्र में संचित ऊर्जा )
- विषय - आधारित समस्याएँ : ( धारिता )
- विषय - आधारित समस्याएँ : ( विविध प्रश्न )
- विषय - आधारित समस्याएँ : ( संधारित्र में संचित ऊर्जा )
- विषय - आधारित समस्याएँ : ( संधारित्रों का संयोजन )