Complete Solutions to Section -C of chapter MODEL TEST PAPER-6 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MODEL TEST PAPER-6 |
| VIVA PUBLICATION | Section -C |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
The line of regression of y on x is given by `1.63x-y=19.36` and regression equation of x on y is `0.596y -x=11.83`. Estimated value of y when x= 13.5 is
View SolutionGiven `r= sqrt((3)/(4)), b_(yx)= (1)/(2)`, variance of x=12, then standard deviation of y is
View Solution`2x+3y-5=0` is the regression equation of x on y. Find its slope
View SolutionFrom the following data find regression equation of y on x, `Sigma x= 55, Sigma y= 88, Sigma x^(2)= 385, Sigma y^(2) = 1114, Sigma xy= 586,n= 10`
View SolutionIf `C(x)= 3ae^(-(x)/(3))` represents the total cost function, find slope of average cost function.
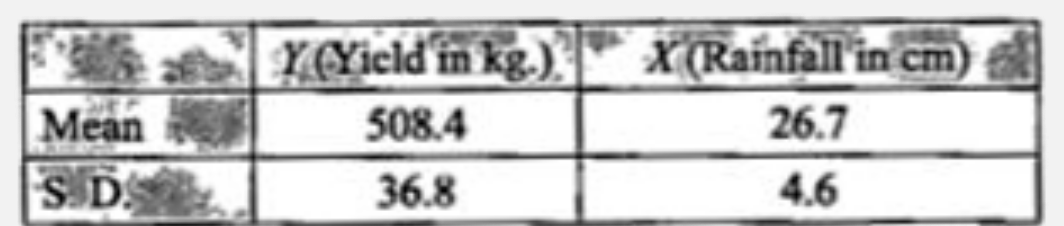
View SolutionYou are given the following data, obtain the regression equation and estimate the yield of crops when the rainfall is 29cm. Given that coefficient of correlation between yield and rainfall= 0.52
View SolutionIn a bivariate distribution, it was found `sigma_(x)=3`, the regression line of Y on X is `8x-10y+66=0` while regression line of X on Y is `40x-18y -214=0`. Calculate r(x,y)
View SolutionA young man rides his motor cycle at 25km/hr, he has to spend Rs 2 per km on petrol, if he rides at a faster speed of 40km/hr, the petrol cost increases to Rs 5/km. He has Rs 100 to spend on petrol and wishes to find maximum distance he can travel within 1 hour. Express this as a linear programming problem and solve it.
View SolutionThe demand function of an output is `x=106-2p`, where x is the output and p is the price per unit and average cost per unit is `5 + (x)/(50)`. Determine the number of units for maximum profit
View SolutionFor the demand function `p= (a)/(x+b)-c`, where `ab gt 0`, show that the marginal revenue decreases with the increase of x.
View Solution
Section -C questions and complete solutions for chapter MODEL TEST PAPER-6 of ARYA MATHS (ENGLISH) of Class 12