Complete Solutions to Section .C. of chapter SELF ASSESSMENT PAPER 06 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | SELF ASSESSMENT PAPER 06 |
| OSWAL | Section .C. |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
The average cost function associated with producing and marketing x units of an item is given by `AC = 3x - 11+ (10)/(x)`. Then MC at x = 2 is
View SolutionIf `sigma_x=5,r =-1/2and b_(yx)=-2/7` , then the value of `sigma_y` is:
View SolutionIf both the coefficient of regression is positive, then the coefficient of correlation is positive or negative?
View SolutionState TRUE or FALSE: can the two lines of regression be perpendicular?
View SolutionFor LPP problems the feasible region always falls on which quadrant?
View SolutionThe average cost function associated with producing and marketing units of an item is given by AC `= 2x - 11 + (50)/x` Find:
the total cost function and marginal cost function
View SolutionThe average cost function associated with producing and marketing x units of an items is given by `AC=2x-11+(50)/(x)`. Find the range of value of the output x, for which AC is increasing.
View SolutionThe manufacturing cost of an item is Rs3 per item, fixed cost is Rs900 and the labour cost is Rs `(x^2)/100` for x items produced. How many items must be produced to have average cost minimum.
View SolutionFor a bivariate date, you are given following information:
` sum x = 125 , sum x^(2) = 1650 , sum y = 100 , sum y^(2) = 1500 , sum xy= 50 , n= 25`
Find line of regression.
View SolutionFind the equations of two lines of regression for the data:
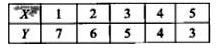
And hence find an estimate of variable Y for X = 3.5 from the appropriate line of regression.
View SolutionTwo tailors A and B earn ₹150 and ₹200 per day respectively. A can stich 6 shirts and 4 pants per day, while B can stitch 10 shirts and 4 pants per day. Form a L.P .P to minimize the labour cost to produce (stitch) at least 60 shirts and 32 pants and solve it graphically.
View Solution
Section .C. questions and complete solutions for chapter SELF ASSESSMENT PAPER 06 of ARYA MATHS (ENGLISH) of Class 12