State TRUE or FALSE: can the two lines of regression be perpendicular?
To determine whether the two lines of regression can be perpendicular, we need to analyze the relationship between the correlation coefficient r and the angles of the regression lines.
1. Understanding Regression Lines:
- The two lines of regression are the regression line of Y on X and the regression line of X on Y.
2. Condition for Perpendicularity:
- The lines of regression will be perpendicular if the angle θ between them is 90∘.
- Mathematically, this can be expressed using the tangent function:
tanθ=1−r2r⋅σxσyσ2x+σ2y
- For the lines to be perpendicular, we set θ=90∘, which implies tan90∘ is undefined (or approaches infinity).
3. Setting Up the Equation:
- When θ=90∘, we have:
tan90∘=∞=1−r2r⋅σxσyσ2x+σ2y
4. Analyzing the Equation:
- The above equation implies that the denominator must approach zero for the fraction to be infinite. Thus:
r⋅σxσyσ2x+σ2y=0
- This can happen if either r=0 or σxσy=0.
5. Conclusion:
- If r=0, it indicates that there is no correlation between X and Y. Therefore, the two lines of regression can indeed be perpendicular.
- Hence, the statement is TRUE.
Final Answer:
TRUE: The two lines of regression can be perpendicular.
- The two lines of regression are the regression line of Y on X and the regression line of X on Y.
- The lines of regression will be perpendicular if the angle θ between them is 90∘.
- Mathematically, this can be expressed using the tangent function:
tanθ=1−r2r⋅σxσyσ2x+σ2y
- For the lines to be perpendicular, we set θ=90∘, which implies tan90∘ is undefined (or approaches infinity).
- When θ=90∘, we have:
tan90∘=∞=1−r2r⋅σxσyσ2x+σ2y
- The above equation implies that the denominator must approach zero for the fraction to be infinite. Thus:
r⋅σxσyσ2x+σ2y=0
- This can happen if either r=0 or σxσy=0.
- If r=0, it indicates that there is no correlation between X and Y. Therefore, the two lines of regression can indeed be perpendicular.
- Hence, the statement is TRUE.
TRUE: The two lines of regression can be perpendicular.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The two line of regression are perpendicular if
Abyx.bxy=1Bbyx.bxy=−1Cbxy.byx=0Dbxy+byx=0If the regression coefficients bxy=1.6 and byx=0.4, and θ is the angle between the two lines of regression, then the value of tanθ is
AA) -0.36BB) 0.72CC) -0.18DD) 0.64
The value of r when the regression lines are perpendicular to each other is:
View SolutionFind the equations of two lines of regression for the data:
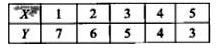
And hence find an estimate of variable Y for X = 3.5 from the appropriate line of regression.
View SolutionState True or False :
Fcl3 exists
View SolutionState True or False:
754÷0=0
View SolutionState True or False:
0÷489=0
View SolutionState True or False:
682÷0=0
View Solution
