Complete Solutions to MULTIPLE CHOICE QUESTION (ASSERTION AND REASON) of chapter MATRICES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MATRICES |
| OSWAL GURUKUL | MULTIPLE CHOICE QUESTION (ASSERTION AND REASON) |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
Assertion (A) : If `A=[(3,-3,4),(2,-3,4),(0,-1,1)]`, then adj (adj A).
Reason (R) : `|"adj( adj A)"| = | A |^((n-1)^(2))` , A be n rowed non-singular matrix
View SolutionAssertion (A) : If
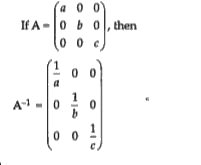
Reason (R) : The inverse of a diagonal matrix is a diagonal matrix.
View SolutionAssertion (A) : The rank of a unit matrix of order `nxxn` is n.
Reason (R) : The rank of a non-singular matrix of order `n xx n` is not n.
View SolutionAssertion (A) : The matrix `[(a,0,0,0),(0,b,0,0),(0,0,c,0)]` is a diagonal matrix.
Reason (R) : A = `[ a_(ij)]` is a square matrix such that `a_("ij") =0AAnej` , then A is called diagonal matrix.
View SolutionAssertion (A) : The inverse of the matrix `A=[(1,1,1),(1,2,3),(1,4,7)]` does not exist.
Reason (R) : The matrix A is singular.
View SolutionAssertion (A) : If A is a matrix of order `n xx n`, then `det (kA) = k^(n) det (A)` or `|kA|= k^(n) |A|`.
Reason (R) : If B is a matrix obtained from A by multiplying any row or column by a scalar k, then detB=k det A or `| B| =k| A|`.
View SolutionAssertion (A) : The matrix
`A=1/3[(1,-2,2),(-2,1,2),(-2,-2,-1)]`
is an orthogonal matrix.
Reason (R) : If A and B are orthogonal, then AB is also orthogonal.
View SolutionAssertion (A) : If A is a skew-symmetric matrix of order , `3xx 3`, then det (A) = 0 or `|A|= 0.`
Reason (R) : If A is a square matrix, then det (A) = det (A')= det (-A').
View SolutionAssertion (A) : The inverse of A= `[(3,4),(3,5)]` does not exist.
Reason (R) : The matrix A is non-singular.
View SolutionAssertion (A) : If a matrix of order `2 xx 2`, commutes with every matrix of order `2 xx 2`, then it is scalar matrix.
Reason (R): A scalar matrix of order `2 xx 2` commutes with every `2 xx 2` matrix.
View SolutionAssertion (A) : The determinant of a matrix A = `[a_(ij)]_(5xx5)` where `a_(ij)+a_(ij)=0` for all i and j is zero.
Reason (R) : The determinant of a skew symmetric matrix of odd order is zero.
View Solution
MULTIPLE CHOICE QUESTION (ASSERTION AND REASON) questions and complete solutions for chapter MATRICES of ARYA MATHS (ENGLISH) of Class 12