Complete Solutions to MATHEMATICS (SECTION A) of chapter JEE MAIN 2021 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE MAIN 2021 |
| JEE MAINS PREVIOUS YEAR | MATHEMATICS (SECTION A) |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
The number of elements in the set `{x in R :(|x| -3) |x+4|=6}` is equal to : then 'a' must be greater then :
04:31View SolutionA card from a pack 52 cards is lost. From the remaining cards , two cards are drawn and are found to be speades. Find the probability that missing card is also a spade.
06:55View SolutionThe locus of the midpoints of the chord of the circle, `x ^(2) + y ^(2) = 25` which is tangent to the hyperbola, `(x ^(2))/( 9) - (y ^(2))/(16)=1` is :
04:41View SolutionThe number of elements in the set `{x in R :(|x| -3) |x+4|=6}` is equal to :
04:31View SolutionConsider three observations a, b and c such that b=a+c. If the standard deviation of a+2, b+2, c+2 is d, then which of the following is true ?
02:41View SolutionLet a vector `a hati + beta hatj ` be obtained by rotating the vector `sqrt3 hati + hatj` by an angle `45^(@)` about the origin in counterclockwise direction in the first quadrant. Then the area of triangle having vertices `(alpha, beta) , (0, beta) and (0,0)` is equal to:
05:22View Solution`Let A = [{:(i, -i), (-i , i):}], i sqrt (-i)` Then, the system of linear equations`A ^(8) [{:(x), (y):}]= [{:(8), (64):}]` has:
03:46View SolutionThe number of roots of the equation,
`(81) ^( sin ^(2)x) + (81) ^( cos ^(2)x) x = 30`
in the interval [0, `pi`] is equal to :04:01View SolutionLet the functions `f: R toR and g: R to R` be defined as :
`f (x) = {{:(x + 2, """" x lt 0), (x ^(2), """" x gt 0) :} and g (x) = {{:( x ^(3) , """"x lt 1), ( 3x -2, """" x gt 1):}`
Then, the number of points in R where (fog)(x) is NOT differentiable is equal to :06:50View SolutionIf y=yır) is the solution of the differential equation, `(dy)/(dx) + 2 y tan x = sin x, y ((pi)/(3))= 0,` then the maximum value of the function y(x) over R is equal to :
06:52View SolutionLet a complex number `z|z| =1,.` satisfy `log _((1)/(sqrt2)) ((|z| +11)/((|z| -1) ^(2)))le 2.` Then, the largest value of |z| is equal to `"_______"`
04:24View Solution`Let S _(K) = sum _(r=1) ^(k) tan ^(-1) (( 6 ^r)/( 2 ^( 2 r + 1) + 3 ^( 2r +1))) .` Then `lim _( k to oo) S _(k)` is equal to :
07:11View SolutionThe range of a R for which the function
`f (x) = (4a -3) (x + log _(e) 5) + 2 (a -7) cot ((x)/(2)) sin ^(2) ((x)/(2)), x ne 2 npi, n in N` has critical points, is :04:33View SolutionIf `"log"_(10) sin x+"log"_(10)cos x=-1 and "log"_(10)(sin x+cosx)=(("log"_(10)n)n-1)/(2)` then the value of n is ____________
05:06View SolutionIf for `x in (0, (pi)/(2) ) , log _(10) sin x + log _(10) cos x =-1 and log _(10) (sin x + cos x) = (1)/(2) ( log _(10) n-1), n gt 0,` then the value of n is equal to :
02:51View SolutionLet the position vectors of two points P and Q be `3 hati - hatj + 2 hatk and hati + 2 hatj -4 hatk,` respectively. Let Rand S be two points such that the direction ratios of lines PR and QS are (4, -1, 2) and (-2, 1, -2), respectively. Let lines PR and QS intersect at T. If the vector `vec(TA)` is perpendicular to both `vec(PR) and vec(QS)` and the length of vector `vec(TA) is sqrt5` units, then the modulus of a position vector of A, is :
11:30View SolutionIf for `a gt 0,` the feet of perpendiculars from the points A(a, - 2a, 3) and B(0,4,5) on the plane Ix +my+nz=0 are points c(0, -a, -1) and D respectively, then the length of line segment CD is equal to :
07:46View SolutionLet P be a plane Ix+my+nz=0 containing the line, `(1-x)/(1) = (y+4)/(2) = (z+2)/(3).` If plane P divides the line segment AB joining points A(-3, -6, 1) and B(2, 4, -3) in ratio k: 1 then the value of k is equal to:
07:44View SolutionIf n is the number of irrational terms in the expansion of `(3 ^(1//4) + 5 ^(1//8)) ^(60) ,` then (n-1) is divisible by :
06:26View SolutionWhich of the following Boolean expression is a tautology ?
03:20View SolutionThe system of equations `kx + y + z =1, x + ky + z = k ` and `x + y + zk = k^(2)` has no solution if k is equal to `:`
03:51View SolutionIf the fourth term in the expansion of `( x + x^(log_(2) x ))^(7)` is 4480 , then the value of x where `x in N` is equal to `:`
05:09View SolutionIf the Boolean expression `( p rArr q ) hArr ( ~q ** p )` is a tautology, then the Boolean expression `p ** ( ~ q )` is equivalent to `:`
07:01View SolutionWhich of the following is true for y(x) that satisfies the differential equation `( dy )/( dx ) = xy -1 +x -y , y (0) = 0 :`
02:33View SolutionChoose the incorrect statement about the two circles whose equations are given below `:`
`x^(2) + y^(2) - 10x - 10 y + 41 = 0` and
`x^(2) + y^(2) - 16x - 10 y + 80 = 0`04:23View SolutionIf `A = ({:(0, sin alpha),(sinalpha,0):})` and det `( A^(2) - ( 1)/( 2) I )=0` , then a possible value of `alpha` is `:`
02:26View SolutionIf `cot^(-1) ( alpha) = cot^(-1)(2) + cot^(-1)(8) + cot^(-1)(18) + cot ^(-1)(32) + "…………"` upto 100 terms , then `alpha` is `:`
04:39View SolutionTwo dices are rolled. If both dices have six faces numbered 1,2,3,5,7 and 11, then the probability that the sum of the numbers on the top faces is less than or equal to 8 is `:`
03:45View SolutionIn a triangle `PQR` , the co-ordinates of the points P and Q are `( -2,4)` and `( 4,-2)` respectively. If the equation of the perpendicular bisector of `PR` is `2x - y+2=0` , then the centre of the circumcircle of the `Delta PQR` is `:`
03:29View SolutionWhich of the following statements is incorrect for the function `g ( alpha)` for `x in R ` sucth that `g( alpha) = int_((pi )/( 6)) ^((pi )/( 3)) ( sin ^(alpha)x)/(cos^(alpha)x + sin ^(alpha)x)dx`
07:07View SolutionWhat is the inverse of the function `y=5^(logx)`?
01:32View SolutionTeam 'A' consists of 7 boys and n girls and Team 'B' has 4 boys and 6 girls. If a total of 52 single matches can be arranged between these two teams when a boy plays against a boy and a girl plays against a girl, then n is equal to `:`
02:57View SolutionLet `vec( a) = 2 hat(i) - 3 hat(j) + 4 hat(k)` and `vec( b) = 7 hat(i) + hat(j) - 6 hat(k)` . If `vec( r ) xx vec( a) = vec( r ) xx vec( b) , vec( r ) . ( hat(i) +2 hat(j) + hat(k)) = -3`, then `vec ( r ). ( 2 hat(i)- 3hat(j) + hat(k))` is equal to `:`
03:31View SolutionIn a school, there are three types of games to be played. Some of the students play two types of games, but none play all the three games. Which Venn diagrams can justify the above statement ?
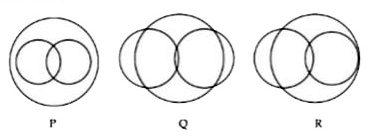 01:20View Solution
01:20View SolutionThe value of `4 + (1)/(5 + (1)/(4+ (1)/(5+ (1)/(4+....oo))))` is
03:27View SolutionArea of the triangle formed by the complex number z, iz and z+iz is __________
08:45View SolutionThe sum of possible values of x for `tan^(-1) ( x + 1) + cot ^(-1) ((1)/( x - 1)) = tan^(-1)((8)/( 31))` is `:`
03:43View SolutionThe equation of the plane which contains the y-axis and passes through the point ( 1,2,3) is `:`
02:38View SolutionThe line `2x-y+1=0` is tangent to the circle at the point (2, 5) and the center of the circle lies on `x-2y=4.` The radius of the circle is
02:16View SolutionThe value of `underset( x rarr 0^(+))( lim) (cos^(-1) ( x- [x]^(2) ). sin^(-1) (x- [ x] ^(2)))/(x- x^(3))` , where [x] denotes the greatest integer `le x ` is `:`
03:48View SolutionLet `f: R -{3} to R-{1}` be defined by f(x) `=(x-2)/(x-3)`
Let `g: R to R` be given as g(x)=2x-3. Then, the sum of all the values of x for which `f^(-1) (x)+g^(-1) (x)=(13)/2` is equal to07:14View SolutionLet `f: R to R` be a function defined as
`f(x)={(,(sin (a+1)x+sin 2x)/(2x), if x lt 0),(, b, if x=0), (,(sqrt(x+bx^(3))-sqrtx)/(bx^(5/2)), if x gt 0):}`
If f is continuous at x=0 then the value of a+b is equal to :06:16View SolutionLet `S_1` be the sum of first 2n terms of an arithmetic progression. Let `S_2` be the sum first 4n terms of the same arithmeti progression. If `(S_(2)-S_(1))` is 1000, then the sum of the first 6n term of the arithmetic progression is equal to :
04:19View SolutionLet in a series of 2n observations, half of them are equal to a and remaining half are equal to -a. Also by adding a b in each of these observation, the mean and standard deviation of a new set become 5 and 20 respectively. Then the value of `a^2+b^2` is equal to :
02:23View SolutionLet `veca and vecb` be two non-zero vectors perpendicular to each other and `|veca|=|vecb|`. If `|veca xx vecb|=|veca|`, then the angle between the vectors `(veca +vecb+(veca xx vecb)) and veca` is equal to :
04:36View SolutionLet a complex number be `w=1-sqrt3`I, Let another complex number z be such that |z w|=1 and arg(z)-arg (w) `=pi/2`. Then the area of the triangle with vertices origin, z and w is equal to :
03:10View SolutionConsider a hyperbola `H : x^(2)-2y^(2) =4`. Let the tangent at a point `P(4, sqrt6)` meet the x-axis at Q and latus rectum at `R (x_(1),y_(1)), x_(1) gt 0`. If F is a focus of H which is nearer to the point P, then the area of `triangleQFR` is equal to
05:29View SolutionLet `g(x)=int_(0)^(x) f(t) dt`, where f is continuous function in [0,3] such that `1/3 le f(t) le 1` for all `t in [0,1] and 0 le f(t) le 1/2` for all ` tin (1,3]`. The largest possible interval in which g(3) lies is:
03:32View SolutionLet the centroid of an equilateral triangle ABC be at the origin. Let one of the sides of equilateral triangle be along the straight line x+y=3. If R and r be the radius of circumcircle and incircle respectively of `triangleABC`, then (R+r) is equal to :
05:03View SolutionIn a triangle ABC, if `|vec(BC)|=8, |vec(CA)|=7, |vec(AB)|=10`, then the projection of the `vec(AB)` on `vec(AC)` is equal to :
02:38View SolutionLet the system of linear equations
`4x+lambda y+2z=0`
`2x-y+z=0`
`mux+2y+3z=0, lambda , mu in R`
has a non-trivial solution. Then which of the following is true?02:53View SolutionIf `15 sin^(4) alpha+10 cos^(4) alpha=6`, some `alpha in R`, then the value of `27 sec^(6) alpha+8 cosec^(6) alpha` is equal to
03:52View SolutionLet a tangent be drawn to the ellipse `x^2/(27) +y^2=1" at "(3sqrt3 cos theta, sin theta)," where "theta in (0,pi/2)`, Then the value of `theta` such that the sum of intercepts on axes made by this tangent is minimum is equal to :
04:36View SolutionThe area bounded by the curve `4y^(2)=x^(2) (4-x) (x-2)` is equal to :
05:07View SolutionDefine a relation R over a class of `n xx n` real matrices A and B as `ARB` iff there exists a non-singular matrix P such that `A=P^(-1)BP`
Then which of the following is true?07:02View SolutionLet in a Binomial distribution, consisting of 5 independent trials, probalitiies of exactly 1 and 2 sucesses be 0.4096 and 0.2048 resepectively. Then the probability of getting exactly 3 sucesses is equal to :
03:43View SolutionLet `S_(1): x^(2)+y^(2)=9 and S_(2) : (x-2)^(2)+y^(2)=1`. Then the locus of centre of a variable circle S which touches `S_1` internally and `S_2` externally always passes through the points:
05:13View SolutionA pole stands vertically inside a triangular park ABC. Let the angle of elevation of the top of the pole from corner of the park be `pi/3`. If the radius of the circumcircle of `triangleABC` is 2. then the height of the pole is equal to :
02:16View SolutionIf P and Q are two statements, then which of the following compound statement is a tautology?
03:46View SolutionLet y=y(x) be the solution of the differential equation `(dy)/(dx)=(y+1) ((y+1)e^(x^(2)/2)-x), 0 lt x lt 2.1,` with y(2)=0. Then the value of `(dy)/(dx)` at x=1 is equal to .
06:10View Solution
MATHEMATICS (SECTION A) questions and complete solutions for chapter JEE MAIN 2021 of JEE MAINS PREVIOUS YEAR of Class 12
