Complete Solutions to SECTION-A of chapter JEE MAIN 2021 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE MAIN 2021 |
| JEE MAINS PREVIOUS YEAR | SECTION-A |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The statement among the following that is a tautology is :
View SolutionA man on the straight line whose arithmetic mean of reciprocal of intercepts on the axes is `1/4`. There are 3 marbles at A (1,1) , B(2,2) , C(4,4) . Then which marble lie on its path
View SolutionThe equation of the plane passing through the point (1, 2, –3) and perpendicular to the planes 3x + y – 2z = 5 and 2x – 5y – z = 7, is
View SolutionThe population p(t) at time t of a certain mouse species satisfies the differential equation `(d p(t))/(dt)=0. 5 p(t)-450` If `p(0)""=""850` , then the time at which the population becomes zero is (1) `2 ln 18` (2) `ln 9` (3) `1/2 ln 18` (4) `ln 18`
View SolutionThe system of linear equation
` 3x - 2y - kz =10`
` 2x - 4y - 2z =6`
` x +2y -z =5m`
is in-consistent if :
View SolutionIf ` f: R to R ` is function defined by ` f(x) = [x-1] cos ( (2x -1)/(2)) pi`, where [.] denotes the greatest integer function , then f is :
View SolutionThe distance of the point (1,1,9) from the point of intersection of the line `(x-3)/1=(y-4)/2 = (z-5)/2` and plane x+y+z=17
View SolutionTangent is drawn to `y=x^3` at `P(t,t^3)` , it intersects curve again at Q.Find ordinate of point which divide PQ internally in 1:2
View SolutionIf `int ( cos x - sin x )/( sqrt(8 - sin 2x ))dx = a sin^(-1) (( sin x + cos x )/(b)) +c ,`where c is a constant of integration, then the ordered pair (a, b) is equal to :
View SolutionValue of `-^(15)C_(1) + 2..^(15)C_(2)- 3.^(15)C_(3) + ...... - 15.^(15)C_(15)+ ^(15)C_(1)+ ^(15)C_(2)+ ....^(15)C_(14)` is
View Solution`f(x) = (4x^3-3x^2)/6 -2Sinx +(2x-1)Cosx` , then `f(x)` is
View SolutionLet `f :R to R` be fefined as f(x) = 2x -1 and ` g : R - {1} to R` be defined as ` g(x) = (x-1/2)/(x-1)` Then the composition function ƒ(g(x)) is :
View SolutionAn ordinary dice is rolled for a certain number of times. If the probability of getting an odd number 2 times is equal to the probability of getting an even number 3 times, then the probability of getting an odd number for odd number of times is :
View SolutionA committee has to be formed from 6 Indians and 8 foreignera such that the number of Indians should be atleast two and foreigners should be double that of Indians. In how many ways can it be formed
View SolutionThe area ( in sq, units ) of the part of the circle `x^2 +y^2 = 36` , which is outside the parabola ` y^2 = 9x ,` is
View SolutionIf `p,q gt0,p+q=2` and `p^4+q^4=272`, then p and q are roots of
View SolutionTwo vertical poles are 150 m apart and the height of one is three times that of the other if from the middle point of the line joining their feet , an observer finds the angles of elvation of their tops ot be complememntary then the height of the shorter pole ( in meters ) is :
View SolutionEvaluate `: lim_(x->0)(int_0^(x^2)sinsqrt(t)\ dt)/(x^3)`
View SolutionIf `e^(( cos^2 x + cos^4x+ cos ^6 x + ……..oo ) log_e 2)` satisfies the equation ` t^2 - 9t + 8=0` , then the value of `( 2 sin x)/( sin x + sqrt(3) cos x) ( 0 lt x lt (pi)/(2))` is
View SolutionThe locus of the midpoint of the segment joining the focus to a moving point on the parabola `y^2=4a x` is another parabola with directrix `y=0` (b) `x=-a` `x=0` (d) none of these
View SolutionA missile fires a target . The probability of getting intercepted is `1/3` and if it is not intercepted then probability of hitting the target is `3/4` . Three independent missiles are fired . Find the probability of all three hit.
View SolutionIf `0 lt theta, phi lt (pi)/(2), x = sum_(n=0)^(oo)cos^(2n)theta, y=sum_(n=0)^(oo)sin^(2n)phi` and `z=sum_(n=0)^(oo)cos^(2n)theta*sin^(2n)phi` then :
View Solution`f(x+1)=f(x) + f(1) , f(x), g(x) : N to N`
`g(x)` = any arbitrary function and `fog(x)` is one-one
View SolutionThe equation of the line through the point (0,1,2) and perpendicular to the line `(x-1)/(2)=(y+1)/(3)=(z-1)/(-2)` is :
View SolutionLet `alpha` be the angle between the lines whose direction cosines satisfy the equation `l+m-n=0`and `l^2+m^2-n^2=0` then value of `(Sinalpha)^4+(Cosalpha)^4` is
View SolutionThe value of the integral
`int (sin theta.sin2theta(sin^(6)theta+sin^(4)theta+sin^(2)theta) sqrt(2sin^(4) theta+3sin^(2)theta+6))/(1-cos2theta)d theta` is :
(where c is a constant of integration)
View SolutionThe value of `int_(-1)^(1)x^(2)e^([x^(3)])dx`, where [t] denotes the greatest integer `le t`, is :
View SolutionA man is observing, from the top of a tower, a boat speeding towards the tower from a certain point A, with uniform speed. At that point, angle of depression of the boat with the man's eye is `30^(@)` (Ignore man's height). After sailing for 20 seconds, towards the base of the tower (which is at the level of water), the boat has reached a point B, where the angle of depression is `45^(@)`. Then the time taken (in seconds) by the boat from B to reach the base of the tower is:
View SolutionA tangent is drawn to the parabola `y^(2) = 6x` which is perpendicular to the line `2x + y = 1`. Which of the following points does NOT lie on it?
View SolutionAll possible values of `theta in [0, 2pi]` for which `sin 2theta +tan 2theta gt 0` lie in :
View SolutionLet the lines `(2-i)z=(2+i) barz` and `(2+i)z+(i-2)barz-4i=0`, (here `i^(2)= -1`) be normal to a circle C. If the line `iz+barz+1+i=0` is tangent to this circle C, then its radius is :
View SolutionThe image of the point (3, 5) in the line `x -y + 1 = 0`, lies on :
View SolutionIf the cuves, `(x^(2))/(a)+(y^(2))/(b)=1 and (x^(2))/(c )+(y^(2))/(d)=1` intersect each other at an angle of `90^(@)`, then which of the following relations is TRUE?
View Solution`lim_(n to oo) (1+(1+(1)/(2)+………+(1)/(n))/(n^(2)))^(n)` is equal to :
View SolutionThe coefficients a, b and c of the quadratic equation, `ax^(2) + bx + c = 0` are obtained by throwing a dice three times. The probability that this equation has equal roots is:
View SolutionThe total number of positive integral solutions (x, y, z) such that xyz = 24 is :
View SolutionIntegral value of k for which `x^2-2(3k-1)x+8k^2-7 gt 0`
View SolutionIf a curve passes through the origin and the slope of the tangent to it at any point (x, y) is `(x^(2)-4x+y+8)/(x-2)`, then this curve also passes through the point:
View SolutionThe statement `A to (B to A)` is equivalent to :
View SolutionIf Rolle's theorem holds for the function `f(x)=x^(3)-ax^(2)+bx-4, x in [1,2]` with `f'((4)/(3))=0`, then ordered pair (a, b) is equal to :
View SolutionIf the vectors `veca` and `vecb` are mutually perpendicular, then `veca xx {veca xx {veca xx {veca xx vecb}}` is equal to:
View SolutionA fair coin is tossed fixed times. The probability of getting 7 heads is equal to probability of getting 9 heads. Then find the probability of getting 2 heads
View SolutionA is `2xx2` symmetric such that trace of `A^2` is 1.How many such matrices are possible with integer entries ?
View SolutionIn a increasing geometric series, the sum of the second and the sixth term is `(25)/(2)` and the product of the third and fifth term is 25. then , the sum of ` 4^(th) , 6 ^(th) and 8^(th)` terms to
View SolutionThe value of `sum_(n=1)^100 int_(n-1)^n e^(x-[x])dx = `
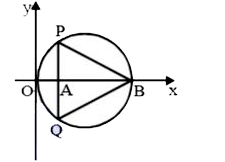
View SolutionIn the circle given below . Let OA = 1 unit , OB = 13 unit and PQ ` bot ` OB. Then the area of the triangle PQB ( in square units)is
View SolutionSum of series `1+2/3+7/3^2+12/3^3 + . . . . . oo`
View Solution`lim_(hrarr0)2((sqrt3Sin(h+pi/6)-Cos(h+pi/6))/(h(sqrt3Cosh-Sinh)))`
View SolutionFind maximum value of term independent of "t" in `(tx^(1/5) + (1-x)^(1/10)/t )^10 , x in (0,1)`
View SolutionGrowth of bacteria is directly proportional to number of bacteria . At t=0 , number of bacteria = 1000 and after 2 hours population is increased by `20%`. After this population becomes 2000 where `t=k/(ln(6/5)`. Find value of `(k/ln2)^2`
View SolutionIf` (1,5,35 ),( 7,5,5),( 1, lamda ,7) and ( 2 lamda ,1,2)` are coplanar then the sum of all possible values of ` lamda ` is
View Solution`Sin^-1x/a=Cos^-1x/b=tan^-1y/c` value of `cos((pic)/(a+b))`
View SolutionThe number of seven digit integers, with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only, is
View SolutionLet f be any function defined on R and let it satisfy the condition :
`| f (x) - f(x) | le ( x-y)^2, AA (x,y) in R ` if ` f(0) =1, ` then :
View Solution`y=1/2x^4-5x^3+18x^2-19x` what will be max. value of slope at
View SolutionThe intersection of three lines
` x-y=0 ,x +2y =3 and 2x +y=6` is a
View SolutionConsider the three planes
`P_1 :3x +15 y +21 z=9`,
` P_2 :x - 3y -z=5 ,` and
` P_3 : 2x +10y +14 z =5`
then , which one of the following is true ?
View SolutionThe value of `|((a+1)(a+2),a+2,1),((a+2)(a+3),a+3,1),((a+3)(a+4),a+4,1)|` is
View SolutionThe value of ` int_(- pi//2) ^(pi//2) ( cos^2 x)/( 1+3^x ) dx ` is
View SolutionLet `P(x,y)` be a point which is a constant distance from the origin. Then equivalence relation of `(1,-1)` is
View SolutionFor the statements p and q, consider the following compound statements :
(a) `(~q ^^ (p to q)) to ~p`
(b) `((p vv q) ^^ ~p) to q`
Then which of the following statements is correct?
View SolutionLet `a, b in R`. If the mirror image of the point P(a, 6, 9) with respect to the line `(x-3)/(7)=(y-2)/(5)=(z-1)/(-9)` is (20, b, -a -9), then |a + b| is equal to :
View SolutionEquation of plane through (1,0,2) and line of intersection of planes `vecr*(hati+hatj+hatk)=1` and `vecr*(hati-2hatj)=-2`
View SolutionIf P is a point on the parabola `y = x^2+ 4` which is closest to the straight line y = 4x – 1, then the co-ordinates of P are :
View SolutionThe angle of elevation of a jet plane from a point A on the ground is `60^@`. After a flight of 20 seconds at the speed of 432 `km//"hour"`, the angle of elevation changes to `30^@`. If the jet plane is flying at a constant height, then its height is :
View SolutionIf `n ge 2` is a positive integer, then the sum of the series `""^(n+1)C_2 + 2(""^2C_2+ ""3C_2 + ""4C_2 +...+ ""nC_2)` is:
View SolutionLet `f(x)={(-55x,,,xlt-5),(2x^3-3x^2-120x,,,-5lexlt4),(2x^3-3x^2-36x+10,,,xge4):}`
Then interval in which f(x) is monotonically increasing is
View SolutionLet f be a twice differentiable function defined on R such that f(0) = 1, f'(0) = 2 and `f '(x) ne 0` for all `x in R`. If `|[f(x)" "f'(x)], [f'(x)" "f''(x)]|= 0`, for all `x in R`, then the value of f(1) lies in the interval:
View SolutionFor which of the following curves, the line `x + sqrt3 y = 2sqrt3` is the tangent at the point `((3sqrt3)/(2), 1/2)` ?
View SolutionThe value of the integral, `int_1^3 [x^2-2x–2]dx` , where [x] denotes the greatest integer less than or equal to x, is :
View SolutionEvaluate `tan(1/4*Sin^-1(sqrt(63)/8))`
View SolutionThe negative of the statement `~p vv (p ^^ q)` is
View SolutionA curve `y=ax^2+bx+c` passing through the point `(1,2)` has slope of tangent at orign equal to 1 , then ordered triplet `(a,b,c)` may be
View SolutionThe area of the region : `R = {(x, y) : 5x^2 le y le 2x^2 + 9}` is :
View SolutionGiven `y=y(x)`passing through (1,2) such that `xdy/dx +y = bx^4` then find b if `int_1^(2) f(x)dx=62/5`
View Solution`f(0)=1 , f(2)=e^2 , f'(x)=f'(2-x)` , then find the value of `int_0^(2)f(x)dx`
View SolutionIf A is symmetric matrix and B is skew symmetric matrix of order `3xx3`, then consider `(A^2B^2-B^2A^2)X=0`, where X is a matrix of unknown variable of `3xx1` and O is a null matrix of `3xx1` , then system of linear equation has
View SolutionLet a, b, c be in arithmetic progression. Let the centroid of the triangle with vertices (a, e), (2, b) and (a, b) be `((10)/(3), 7/3)`. If `alpha, beta` are the roots of the equation `ax^2 + bx + 1 = 0`, then the value of `alpha^2 + beta^2 - alpha beta` is :
View SolutionFor the system of linear equations :
x - 2y = 1, x - y + kz = -2, ky + 4z = 6, `k in R`, consider the following statements :
(A) The system has unique solution if `k ne 2, k ne - 2`.
(B) The system has unique solution if k = - 2.
(C) The system has unique solution if k = 2.
(D) The system has no-solution if k = 2.
(E) The system has infinite number of solutions if `k ne 2`.
Which of the following statements are correct?
View SolutionThe probability that two randomly selected subsets of the set {1, 2, 3, 4, 5} have exactly two elements in their intersection, is :
View SolutionLet `hati+yhatj+zhatk` and `xhati-hatj+hatk` are parallel then unit vector parallel to `xhati+yhatj+zhatk`
View SolutionLet A = {1,2,3,…..10} and `f:ArarrA` be defined as `f(k)={{:(k+1," if k is odd"),(k," if k is even"):}`
Then the number of possible functions g:`ArarrA` such that gof=f is
View SolutionLet `f:RrarrR` be defined as `f(x)={{:(2sin(-(pix)/2)",",if xlt-1),(|ax^2+x+b|",",if -1lexle1),(sin(pix)",",if xgt1):}`
If f(x) is continuous on R , then a+b equals
View Solution`f(x)=int_1^x lnt/(1+t) dt , f(e)+f(1/e)=`
View SolutionThe prime factorization of a number 'n' is given as `n=2^x xx 3^y xx 5^z , y+z=5 and y^-1+z^-1 =5/6` . Find out the odd divisors of n including 1
View SolutionLet `f(x)= sin^(-1)x and g(x) = (x^2-x-2)/(2x^2-x-6)`. If `g(2)=underset(xrarr2)(lim)g(x)` then the domain of the function fog is
View SolutionThe triangle of maximum area that can be inscribed in a given circle of radius 'r' is
View SolutionLet L be a line obtained from the intersection of two planes x+2y+z = 6 and y+2z=4 . If point `P(alpha,beta,gamma)` is the foot of perpendicular from (3,2,1) on L then the value of `21(alpha+beta+gamma)` equals .
View SolutionLet `F_1(A,B,C)=(A^^~B)vv[~C^^(AvvB)]vv~A and F_2(A,B)=(AvvB)vv(BrarrA)` be two logical expressions. Then :
View SolutionThe slope of the tangent to curve is `(xy^2+y)/x` and it intersects the line `x+2y=4` at `x=-2. If (3,y)` lies on the curve then y is
View SolutionLocus of the mid-point of the line joining (3,2) and point on `(x^2+y^2=1)` is a circle of radius r . Find r
View SolutionConsider the following system of equations :
`{:(x+2y-3z=a),(2x+6y-11z=b),(x-2y+7z=c","):}`
where a, b and c are real constant. Then the system of eqations :
View SolutionIf `0 lt a,b lt 1 and tan^(-1)a+tan^(-1) b = pi/4`, then the value of
`(a+b)-((a^2+b^2)/2)+((a^3+b^3)/3)-((a^4+b^4)/4)+...` is :
View SolutionThe sum of the series `sum_(n=1)^oo(n^2+6n+10)/((2n+1)!)` is equal to
View Solution`f(x)` is differentiable function at `x=a` such that `f'(a)=2 , f(a)=4.` Find `lim_(xrarra) (xf(a)-af(x))/(x-a)`
View SolutionLet `A(1,4)` and `B(1,-5)` be two points let p be the point on `(x-1)^2+(y-1)^2=1`. Find maximum value of `(PA)^2+(PB)^2`
View SolutionMirror image of point `(1,3,5)` w.r.t plane `4x-5y+2z=8` is `(alpha,beta,gamma)` then `5(alpha+beta+gamma)`
View Solution`f(x)=int_0^x e^t f(t)dt+e^x , f(x)` is a differentiable function on `x in R` then `f(x)=`
View SolutionIf `A_1` is area between the curve `y=Sinx , y=Cosx` and y-axis in 1st quadrant and `A_2` is area between `y=Sinx , y=Cosx` x=`pi/2` and x-axis in 1st quadrant . Then find `A_2/A_1`
View SolutionA seven digit number is formed using digits 3,3,4,4,4,5,5. The probability, that number so formed is divisble by 2, is:
View Solution
SECTION-A questions and complete solutions for chapter JEE MAIN 2021 of JEE MAINS PREVIOUS YEAR of Class 12