Complete Solutions to Solved Examples of chapter APPLICATIONS OF INTEGRALS - FOR COMPETITION of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATIONS OF INTEGRALS - FOR COMPETITION |
| KC SINHA | Solved Examples |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Find the area of the region bounded by the x-axis and the curves defined by `y=tanx(w h e r e-pi/2lt=xlt=pi/3)` and `y=cotx(w h e r epi/6lt=xlt=(3x)/2)` .
View SolutionFind the area bounded by the curves `x^2+y^2=4,x^2=sqrt(2)y ,a n dx=ydot`
View SolutionFind the area bounded by the curves `x^2+y^2=25 ,4y=|4-x^2|,` and `x=0` above the x-axis.
View SolutionFind the area of the region bounded by the curve C : y=tan x ,tangent drawn to C at x=pi/4, and the x-axis.
View SolutionThe area bounded by the curve `y = x(x - 1)^2,` the y-axis and the line `y = 2` is
View SolutionThe area between the curve `y=2x^4-x^2,` the axis, and the ordinates of the two minima of the curve is 11/60 sq. units (b) 7/120 sq. units 1/30 sq. units (d) 7/90 sq. units
View SolutionCompute the area of the region bounded by the curves `y=ex log_(e)x and y=(log x)/(ex).`
View SolutionThe line `y=m x` bisects the area enclosed by the curve `y=1+4x-x^2` and the lines `x=0,x=3/2 and y=0.` Then the value of `m` is
View SolutionLet `f(x)=M a xi mu m{x^2,(1-x)^2,2x(1-x)},` where `0lt=xlt=1.` Determine the area of the region bounded by the curves `y=f(x),x-a xi s ,x=0,` and `x=1.`
View SolutionA curve `y=f(x)` passes through the origin. Through any point `(x,y)` on the curve, lines are drawn parallel to the coordinate axes. If the curve divides the area formed by these lines and coordinates axes in the ratio `m : n` , find the curve.
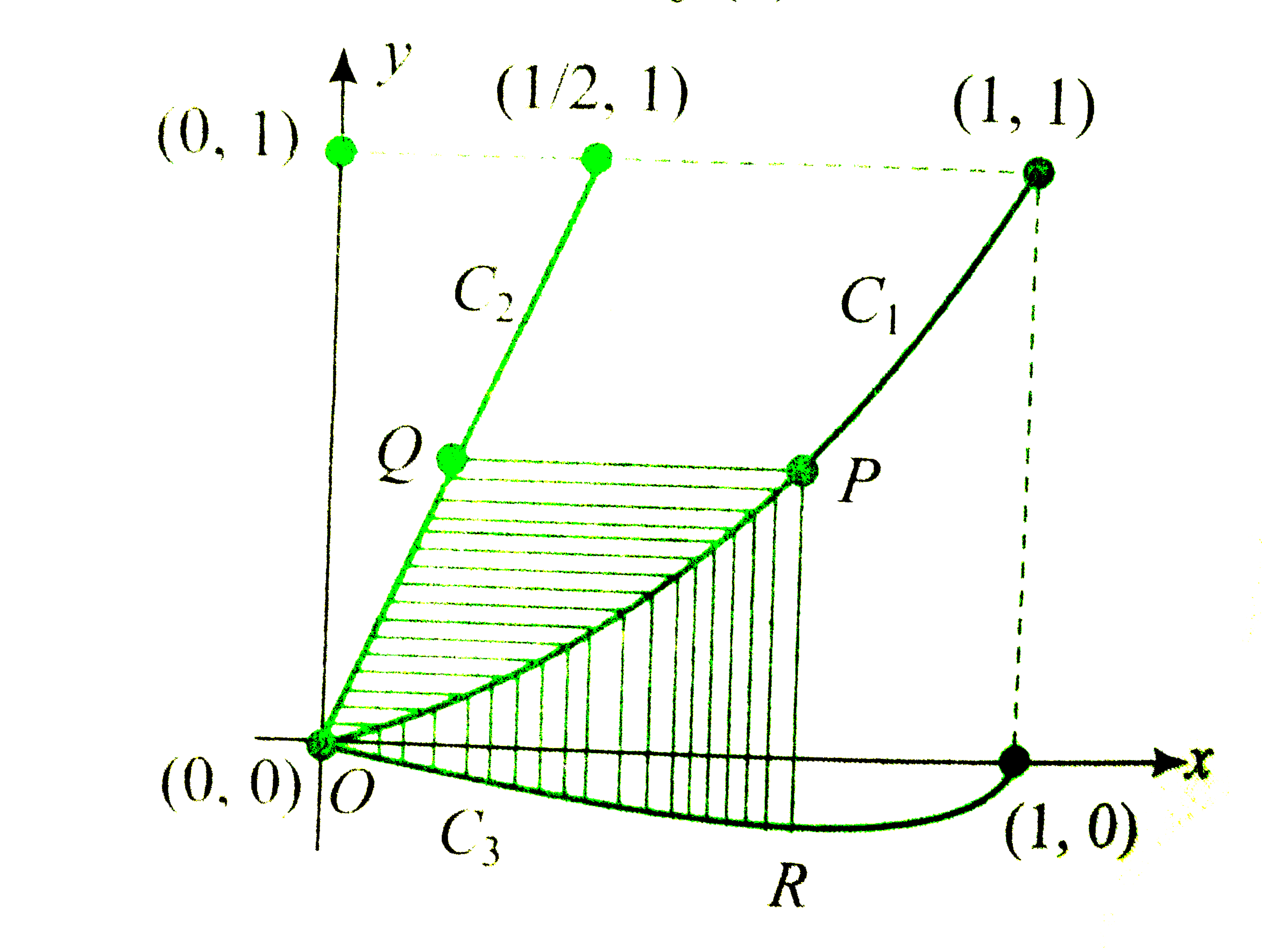
View SolutionLet `C_(1) and C_(2)` be the graphs of the functions `y=x^(2) and y=2x,` respectively, where `0le x le 1." Let "C_(3)` be the graph of a function y=f(x), where `0lexle1, f(0)=0.` For a point P on `C_(1),` let the lines through P, parallel to the axes, meet `C_(2) and C_(3)` at Q and R, respectively (see figure). If for every position of `P(on C_(1)),` the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionFind the ratio of the areas in which the curve `y=[(x^3)/(100)+x/35]` divides the circle `x^(2)+Y^(2)-4x+2y+1=0`. (where, [.] denotes the greated integer function).
View SolutionFind the area of the region formed by `x^(2)+y^(2)-6x-4y+12 le 0, y le x` and `2x le 5`.
View SolutionFind all the possible values of `b >0,` so that the area of the bounded region enclosed between the parabolas `y=x-b x^2a n dy=(x^2)/b` is maximum.
View SolutionConsider a square with vertices at `(1, 1), (-1, 1), (-1, -1) and (1, -1)`. Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionLet `A_n` be the area bounded by the curve `y=(tanx)^n` and the lines `x=0,y=0,` and `x=pi/4dot` Prove that for `n >2,A_n+A_(n-2)=1/(n-1)` and deduce `1/(2n+2)
View SolutionLet `f(x)` be continuous function given by `f(x)={2x ,|x|lt=1`and `x^2+a x+b ,|x|>1}dot`
Find the area of the region in the third quadrant bounded by the curves `x=-2y^2a n dy=f(x)` lying on the left of the line `8x+1=0.`
View SolutionSketch the region included between the curves `x^(2)+y^(2)=a^(2)` and `sqrt(|x|)+sqrt(|y|)=sqrt(a)(a.0)` and find its area.
View SolutionThe area of the region bounded by the parabola `(y-2)^(2)=x-1`, the tangent to the parabola at the point (2,3) and the X-axis is
View SolutionFind the area of the region given by `x+y le 6, x^2+y^2 le 6y` and `y^2 le 8x`.
View SolutionLet `b!=0` and for `j=0,1,2,....,n`. Let `S_(j)` be the area of the region bounded by Y_axis and the curve `x cdot e^(ay)=sin by, (jpi)/bleyle((j+1)pi)/(b)`. Show that `S_(0),S_(1),S_(2),...S_(n)` are in geometric progression. Also, find their sum for a=-1 and `b=pi`.
View SolutionFind the area bounded by the curve `x^2=y ,x^2=-ya n dy^2=4x-3`
View SolutionIf [4a2 4a 1 4b2 4b 1 4c2 4c 1] [f-1 f1 f2] = [3a2 + 3a 3b2 + 3b 3c2 + 3c] fx is a quadratic function and its maximum value occurs at a point V. A is a point of intersection of y = f x with x-axis and point .B is such that chord AB subtends a right angled at V. Find the area enclosed by fx and chord AB.
View SolutionFind the area of the region bounded by the curves `y=x^(2), y=|2-x^(2)|, and y=2,` which lies to the right of the line x=1.
View SolutionThe area bounded by the parabolas `y=(x+1)^2` and `y=(x-1)^2a n dy=(x-1)^2` and the line `y=1/4` is 4 sq. units (b) 1/6 sq. units 4/3 sq. units (d) 1/3 sq. units
View SolutionThe area of the region between the curves `y=sqrt((1+sinx)/(cos x))` and `y=sqrt((1-sin x)/(cos x))` and bounded by the lines `x=0` and `x=(pi)/(4)` is
View SolutionConsider the function `f(x)={{:(x-[x]-(1)/(2),x !in),(0, "x inI):}` where [.] denotes the fractional integral function and I is the set of integers. Then find `g(x)max.[x^(2),f(x),|x|},-2lexle2.`
View SolutionConsider the function `f(x)={{:(x-[x]-(1)/(2),x !in),(0, "x inI):}` where [.] denotes the fractional integral function and I is the set of integers. Then find `g(x)max.[x^(2),f(x),|x|},-2lexle2.`
View Solution
Solved Examples questions and complete solutions for chapter APPLICATIONS OF INTEGRALS - FOR COMPETITION of KC SINHA ENGLISH of Class 12