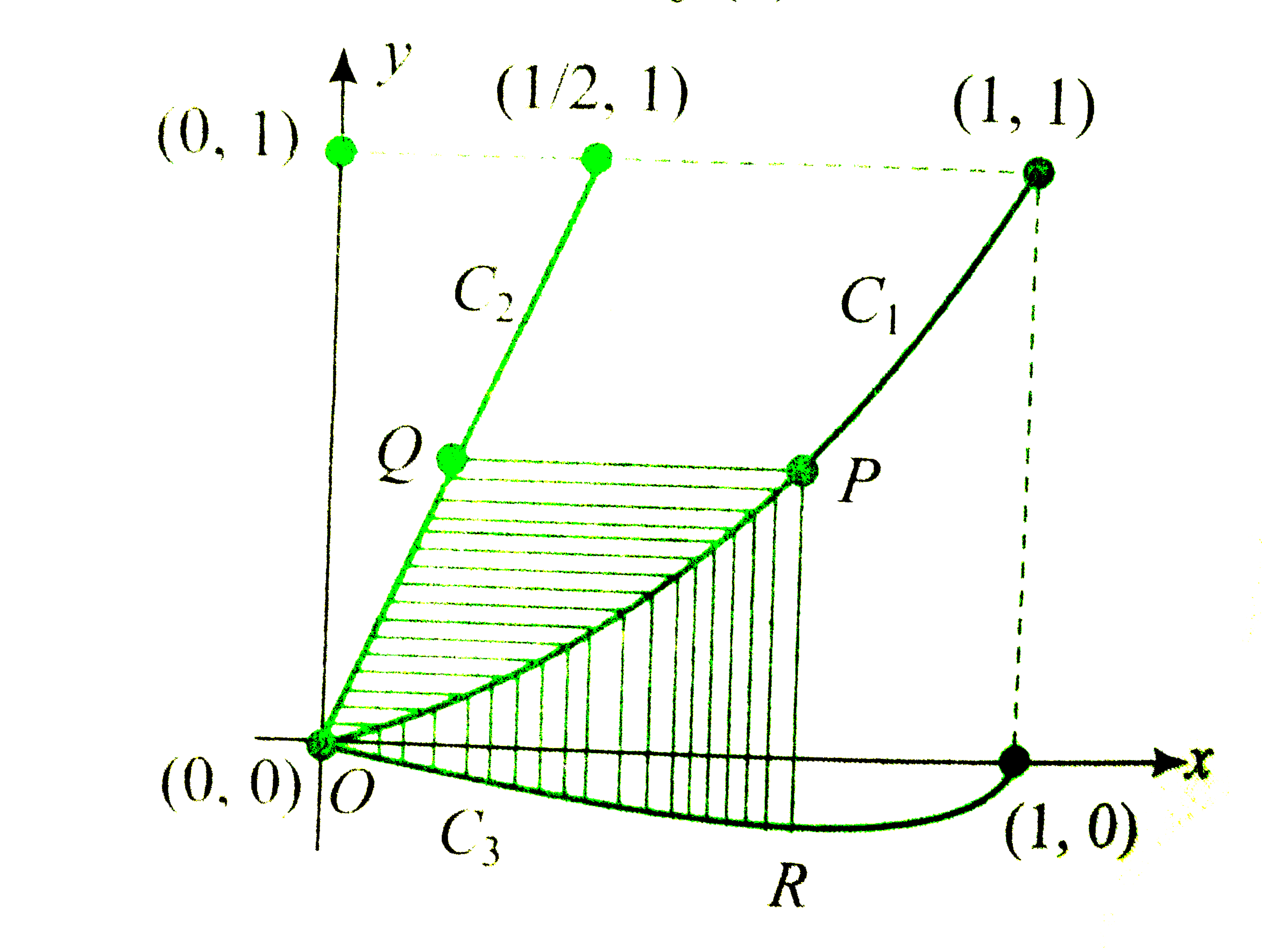
Let C(1) and C(2) be the graphs of the functions y=x^(2) and y=2x, res

Let $C_{1} C_{2}$ be the graphs of the functions $y = x^{2}$ and $y = 2 x,$ respectively, where $0 \leq x \leq 1 .$ Let $C_{3}$ be the graph of a function $y = f (x),$ where $0 \leq x \leq 1, f (0) = 0 .$ For a point $P$ on $C_{1},$ let the lines through $P,$ parallel to the axis, meet $C_{2}$ and $C_{3}$ at $Q$ and $R,$ respectively (see Figure). If for every position of $P (o n C_{1}),$ the areas of the shaded regions $O P Q$ and $O R P$ are equal, determine the function $f (x)$

View Solution

Let C be the centroid of the triangle with vertices (3, -1) (1, 3) and ( 2, 4). Let P be the point of intersection of the lines $x + 3 y - 1 = 0$ and $3 x - y + 1 = 0$ . Then the line passing through the points C and P also passes through the point :

View Solution

Let $f (x) = max {x^{2}, {(1 - x)}^{2}, 2 x (1 - x)}$ where $0 \leq x \leq 1$ . Determine the area of the region bounded by $y = f (x)$ , x-axis, x = 0 and x = 1.

View Solution

Two circles $C_{1}$ and $C_{2}$ intersect at two distinct points $P$ and $Q$ in a line passing through $P$ meets circles $C_{1}$ and $C_{2}$ at $A$ and $B$ , respectively. Let $Y$ be the midpoint of $A B$ and $Q Y$ meets circles $C_{1}$ and $C_{2}$ at $X$ a n d $Z$ respectively. Then prove that $Y$ is the midpoint of $X Z$

View Solution

The circle C1 : $x^{2} + y^{2} = 3$ , with center at O, intersects the parabola $x^{2} = 2 y$ at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3, respectively. Suppose C2 and C3 have equal radii $2 \sqrt{3}$ and centers Q2 and Q3, respectively.If $Q_{2} and Q_{3}$ lies on the y-axis, then

View Solution

Let $C_{1}$ and $C_{2}$ be parabolas $x^{2} = y - 1$ and $y^{2} = x - 1$ respectively. Let P be any point on $C_{1}$ and Q be any point $C_{2}$ . Let $P_{1}$ and $Q_{1}$ be the reflection of P and Q, respectively w.r.t the line y = x then prove that $P_{1}$ lies on $C_{2}$ and $Q_{1}$ lies on $C_{1}$ and $P Q \geq [P P_{1}, Q Q_{1}]$ . Hence or otherwise , determine points $P_{0}$ and $Q_{0}$ on the parabolas $C_{1}$ and $C_{2}$ respectively such that $P_{0} Q_{0} \leq P Q$ for all pairs of points (P,Q) with P on $C_{1}$ and Q on $C_{2}$

View Solution

Let $C_{1}$ and $C_{2}$ be respectively, the parabolas $x^{2} = y - 1$ and $y^{2} = x - 1$ Let P be any point on $C_{1}$ and Q be any point on $C_{2}$ . Let $P_{1}$ and $Q_{1}$ be the refelections of P and Q, respectively with respect to the line y=x.
If the point $p (π, π^{2} + 1)$ and $Q (μ^{2} + 1, μ)$ then $P_{1}$ and $Q_{1}$ are

View Solution

Let $C_{1}$ and $C_{2}$ be respectively, the parabolas $x^{2} = y - 1$ and $y^{2} = x - 1$ Let P be any point on $C_{1}$ and Q be any point on $C_{2}$ . Let $P_{1}$ and $Q_{1}$ be the refelections of P and Q, respectively with respect to the line y=x.
Arithemetic mean of $P P_{1}$ and $Q Q_{1}$ is always less than

View Solution

Let C be a circle with centre $P_{0} and A B$ be a
diameter of C . suppose $P_{1}$ is the midpoint of line
segment $P_{0} B, P_{2}$ the midpoint of line segment
$P_{1} B$ and so on Let $C_{1}, C_{2}, C_{3}$ be circles with diameters $P_{0} P_{1}, P_{1} P_{2}, P_{2} P_{3}$ ,... respectively
Suppose the circles $C_{1}, C_{2}, C_{2},$ ... are all shaded
The ratio of the area of the unshaded portion of C
to that of the original circle is

View Solution

Let the circles
$S_{1} \equiv x^{2} + y^{2} + 4 y - 1 = 0$
$S_{2} \equiv x^{2} + y^{2} + 6 x + y + 8 = 0$
touch each other . Also, let $P_{1}$ be the point of contact of $S_{1}$ and $S_{2}$ , $C_{1}$ and $C_{2}$ are the centres of $S_{1}$ and $S_{2}$ respectively.
The coordinates of $P_{1}$ are

View Solution

Similar Questions

Recommended Questions