Complete Solutions to PART - A of chapter BOARD'S QUESTION PAPER MARCH - 2020 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | BOARD'S QUESTION PAPER MARCH - 2020 |
| KUMAR PRAKASHAN | PART - A |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
Area bounded by curve
`y = tan pi x, x in [- (1)/(4) , (1)/(4) ]` and X - axis is ….....
View SolutionIf the area of the region bounded by two curves ` y=x^2 and y=x^3 ` is `(k)/(6)` then k=…….
View SolutionArea bounded by the ellipse ` (x^2 )/(4) +(y^2)/(16) =4` is …….
View SolutionThe order and degree of the differential equation `(y''')^(3) + (y'')^(4) + (y')^(4) + y=7` are …..... Respectively.
View SolutionThe number of arbitrary constant the particular solution of a differential equation of order 4 will be ........
View SolutionIntegrating factor of the differential equation `y dx - ( x-2y^(2) ) dy=0` is …..
View SolutionMeasure of the angle between the vector `vec(a)=hati-hatj+hatk` and `vec(b)=hati+hatj+hatk` is …………..
View SolutionIf `overset(to) (a) = hat(i) + 2 hat(j) + hat(k) and overset(to)(b) = hat(i) - 2 hat(j) - 3 hat(k)` then `( overset(to)(a) + overset(to)(b) ). ( overset(to)(a) - overset(to)(b) ) = …......`
View SolutionFind the area of a parallelogram whose adjacent sides are given by the vectors `overset(to)(a) = 3 hat(i) + 5 hat(j) - 2 hat(k) and overset(to)( b) = 2 hat(i) + hat(j) + 3 hat(k)`.
View SolutionLet `|overset(to)(x) | = |overset(to)(y)| = |overset(to)(x) + overset(to)(y) | = 1` and if measure of the angle between `overset(to)(x) and overset(to)(y)` is `alpha`, then `sin alpha= ......`
View Solution`hat(i). ( hat(k) xx hat(j)) + hat(j) .(hat(i) xx hat(k) ) + hat(k). ( hat(j) xx hat(i) ) + hat(i). (hat(i) xx hat(j) ) + hat(j) . ( hat(j) xx hat(k) ) =...........`
View SolutionFor three vectors `vec(a),vec(b)` and `vec( c ),vec(a)+vec(b)+vec( c )=vec(0)|vec(a)|=3,|vec(b)|=4,|vec( c )|=5`, then evaluate
`2(vec(a)*vec(b)+vec(b)*vec( c )+vec( c )*vec(a))`.
View SolutionIf the lines `(2x-5)/(k) = (y+2)/(-5) = (z)/(1)` and `(x)/(1) = (y)/(2) = (z)/(3)` are perpendicular to each other, then value of k is....................
View SolutionIf the plane `2x + 3y + 4z=1` intersects X-axis, Y-axis and Z-axis at the points A, B and C respectively, then the centroid of a `Delta ABC` is …....
View SolutionDistance between the two planes `2x -2y + z= 5 and 6x-6y + 3z = 25` is …... Units.
View SolutionThe objective function of a linear programming problem is ..........
View SolutionThe vertices of the feasible region determined by some linear constraints are `(0,2), (1,1),(3,3), (1,5)`. Let `Z=px + qy` where `p,q gt 0`. The condition on `p and q` so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is .......
View SolutionIf the vertices of a feasible region are `O(0,0),A(10,0), B(0,20), C(15, 15)`, then minimum value of a objective function `Z= 10 x - 20y + 30` is….......
View SolutionIf P(E ) = 0.8, P(F) = 0.5 and `P(E cap F) = 0.4` then `P( E//F)=….......`
View SolutionA random variable X has the following probability distribution :
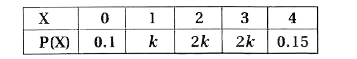
then `P(X le 1) = ….......`
View SolutionChoose the correct answer
The probability of obtaining an even prime number on each die, when a pair of dice is rolled is
View SolutionLet R be the relation on the set N given by `R= { (a, b): a= b-2, b gt 6}`. Choose the correct answer.
View Solution`a**b = (ab)/(1)` defined on Q. Inverse of `0.001` is…........
View SolutionFor sets `S= { pi, pi^(2) , pi^(3) } and T= {e, e^(2) , e^(3) }` if `F^(-1) : T to S` is defined as `F^(-1) = { ( e, pi^(3) ) , (e^(2) , pi^(2) ), (e^(2) , pi)}`, then function `F=.........`
View Solution`sum_(i=0)^(2) cot^(-1) { - (i+1)} = …....` .
View SolutionWhich of the following is a graph of `f(x) = tan^(-1) x , ( x in R)` ?
View Solution`sec^(-1) x + cosec^(-1) x + cos^(-1) (x^(-1) ) + sin^(-1) ( x^(-1) ) = …..` (where `|x| ge 1 , x in R` )
View Solution`cot{ (2019pi)/(2) - ( cosec^(-1) (5)/(3) + tan^(-1)"" (2)/(3) ) } = .....`
View SolutionConstruct a `3 xx 4` matrix, elements are given by `a_(ij) = |-3i + 4j|`.
View SolutionA is `3xx3` matrix and det(A) `=7`. IF B = adj A then det(AB)= …........
View SolutionIf `A = [{:(3,1),(-1,2):}] and A^(2) - 5A= kI` then `k=.........`
View SolutionMatrices X and Y are inverse of each other then........
View SolutionIf `Delta = abs{:(x+y+z^(2) , x^(2) + y+ z, x+y^(2) + z),(z^2, x^2, y^2),(x+y,y+z,x+z):}`, (where `( x ne y ne z) x, y, z in R- {0}` ) then `Delta= ........`
View SolutionFor `Delta = abs{:(2019, 2020, 2021),(2022,2023,2024),(2025, 2026, 2027):}` sum of minor and cofactor of 2020 is.........
View SolutionIf area of triangle is 35 sq. units with vertices `(2,-6), (5,4)and (k,4)`, then `k=…......`
View SolutionLet the function `f` be defined by
`f(x) ={{:(cx+1",", "if", x ge 3),(dx + 3",","if", x lt 3):}`
If `f` is continuous at `x = 3` then `d - c = ........`
View SolutionDifferentiate the functions `(x+ 3)^(2).(x+ 4)^(3).(x+ 5)^(4)`
View SolutionIf `y= log_(e) ( log_(pi) x) , ( x gt 1)` then `( d^2 y)/( dx^2) = …....`
View SolutionFind the point at which the tangent to the curve `y=sqrt(4x-3)-1` has its slope `(2)/(3)`.
View SolutionApproximate value of `sqrt(0.081) = ….....`
View SolutionFunction `f(x) = |sinx|, x in (- (pi)/(2) , 0)` is :
View SolutionThe local maximum value of `f(x)=x+(1)/(x)` is ………….
View Solution`intsqrt( ( cos x - cos^(3) x)/( 1 - cos^(3) x)) dx = ........+ C`. ( where `x in R - { (kpi)/( 2)//k in Z}` )
View SolutionIf `int (1)/( e^(x) + 1) dx= px- q log |1+e^(x) | + C` then `p+q=….........`
View Solution`int e^(x^3) . 5^(x^2) . x. [2log 5+ 3x] dx = …...... + C`.
View Solution`int( dx)/( sqrt( 2x - x^(2) ) ) = …...... +C`.
View Solution`int_(-1)^( sqrt3) (dx)/( 1+x^2) = …...... .`
View Solution`int_(0)^(pi) cos^(3)x . Sin^(4) x dx = …... `.
View Solution`int_(- (pi)/(6) )^((pi)/(6) ) sin^(5) x cos^(2) x dx = ….....`.
View Solution`int_(0)^(2) f(x) dx = …...`, where `f(x) = ` max `{x, x^(2) }`.
View Solution
PART - A questions and complete solutions for chapter BOARD'S QUESTION PAPER MARCH - 2020 of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 12