Complete Solutions to TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| KUMAR PRAKASHAN | TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
Solve the following linear programming problem graphically :
Maximise Z = 4x + y `" …(1)"`
subject to the constraints :
`x+y le 50 " …(2)"`
`3x+y le 90" …(3)`"
`x ge 0, y ge 0" ...(4)"`
View SolutionSolve the following linear programming problem graphically :
Minimise Z = 200 x + 500 y `" …(1)"`
subject to the constraints :
`x+2y ge 10" …(2)"`
`3x+4y le 24" …(3)"`
`x ge 0, y ge 0" ...(4)"`
View SolutionSolve the following problem graphically :
Minimise and Maximise Z = 3x + 9y `" …(1)"`
subject to the constraints : `x+3y le 60" …(2)"`
`x+y ge 10 " …(3)"`
`x le y" …(4)"`
`x ge 0, y ge 0" …(5)"`
View SolutionDetermine graphically the maximize value of the subjective function `Z = 10x + 25y` `" …(1)"`
subject to the constraints :
`x le 3, y le 3" …(2)"`
`x+y le 5" …(3)"`
`x ge 0, y ge 0" .. .(4)"`
View SolutionMinimise Z = 3x + 2y
subject to the constraints :
`x+y ge 8" …(1)"`
`3x+5y le 15" …(2)"`
`x ge 0, y ge 0" …(3)"`
View Solution(Diet problem): A dietician wishes to mix two types of foods in such a way that vitamin contents of the mixture contain atleast 8 units of vitamin A and 10 units of vitamin C. Food 'I' contains 2 units/kg. of vitamin A and 1 unit/kg. of vitamin C. Food 'II' contains 1 unit/kg. of vitamin A and 2 units/kg of vitamin C. It costs Rs. 50 per kg. to purchase Food 'I' and Rs. 70 per kg. to purchase Food 'II'. Formulate this problem as a linear programming problem to minimise the cost of such a mixture.
View Solution(Allocation problem) A cooperative society of farmers has 50 hectare of land to grow two crops X and Y. The profit from crops X and Y per hectare are estimated as Rs. 10,500 and Rs. 9000 respectively. To control weeds, a liquid herbicide has to be used for crops X and Y at rates of 20 litres and 10 litres per hectare. Further, no more than 800 litres of herbicide should be used in order to protect fish and wild life using a pond which collects drainage from this land. How much land should be allocated to each crop so as to to maximise the total profit of the society ?
View Solution(Manufacturing problem) A manufacturing company makes two models A and B of product. Each piece of Model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of Model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of Rs. 8000 on each piece of model A and Rs. 12000 on each piece of Model B. How many pieces of model A and model B should be manufactured per week to realise a maximum profit ? What is the maximum profit per week ?
View Solution(Diet problem) A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholestrol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholestrol. How many packets of each food should be used to minimise the amount of vitamin A in the diet ? What is the minimum amount of vitamin A ?
View Solution(Manufacturing problem) A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine III must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of M and N on the three machines are given in the following table :
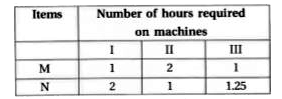
She makes a profit of Rs. 600 and Rs. 400 on items M and N respectively. How many of each should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit ?
View Solution(Transportation problem) There are two factories located one place at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below :

How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost ?
View Solution
TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK questions and complete solutions for chapter LINEAR PROGRAMMING of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 12