Complete Solutions to SECTION C NCERT EXEMPLAR SOLUTION (Long Answer Type Questions) of chapter ELECTROMAGNETIC WAVES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC WAVES |
| KUMAR PRAKASHAN | SECTION C NCERT EXEMPLAR SOLUTION (Long Answer Type Questions) |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
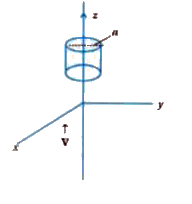
An infinitely long thin wire carrying a uniform linear static charge density `lambda` is placed along the z - axis. The wire is set into motion along its length with a uniform velocity `V=v hat(k)_(z)`. Calculate the pointing vector `S=(1)/(mu_(0))(vec(E )xx vec(B))`.
View SolutionSea water at frequency `v=4xx10^(8)` Hz has permittivity `in ~~ 80 in_(0)`, permeability `mu = mu_(0)` and resistivity `rho = 0.25 Omega`, Imagine a parallel plate capacitor immersed in sea water and driven by an alternating voltage source `V(t)=V_(0)sin 2pi vt`. What fraction of the conduction current density is the displacement current current density ?
View SolutionA long straight cable of length l is placed symmetrically along z - axis and has radius `a(lt lt l)`. The cable consists of a thin wire and a co-axial conducting tube. An alternating current thin wire and returns along the coaxial conducting tube. The induced electric field at a distance s from the wire inside the cable is `vec(E )(s, t)=mu_(0)I_(0)v cos (2pi vt) ln ((s)/(a))hat(k)`
Calculate the displacement current density inside the cable.
View SolutionA long straight cable of length l is placed symmetrically along z - axis and has radius `a(lt lt l)`. The cable consists of a thin wire and a co-axial conducting tube. An alternating current thin wire and returns along the coaxial conducting tube. The induced electric field at a distance s from the wire inside the cable is `vec(E )(s, t)=mu_(0)I_(0)v cos (2pi vt) ln ((s)/(a))hat(k)`
Integrate the displacement current density across the cross - section of the cable to find the total displacement current `I^(d)`.
View SolutionA long straight cable of length l is placed symmetrically along z - axis and has radius `a(lt lt l)`. The cable consists of a thin wire and a co-axial conducting tube. An alternating current thin wire and returns along the coaxial conducting tube. The induced electric field at a distance s from the wire inside the cable is `vec(E )(s, t)=mu_(0)I_(0)v cos (2pi vt) ln ((s)/(a))hat(k)`
Compare the conduction current `I_(0)` with the displacement current `I_(0)^(d)`.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by `vec(E )=E_(0)sin (kz - omega t)hat(i)` and `vec(B)=B_(0)sin(kz - omega t)hat(j)`.
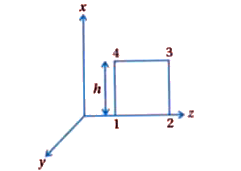
Evaluate `int vec(E ). Vec(d)l` over the rectangular loop 134 shown in figure.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by `vec(E )=E_(0)sin (kz - omega t)hat(i)` and `vec(B)=B_(0)sin(kz - omega t)hat(j)`.
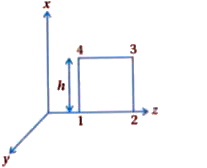
Evaluate `int vec(B).vec(d)s` over the surface bounded by loop 1234.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by `vec(E )=E_(0)sin (kz - omega t)hat(i)` and `vec(B)=B_(0)sin(kz - omega t)hat(j)`.
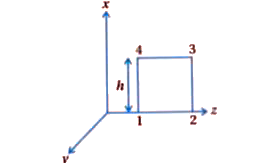
Use equation `int vec(E ).vec(d)l =-(d phi_(B))/(dt)` to prove `(E_(0))/(B_(0))=c`.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by `vec(E )=E_(0)sin (kz - omega t)hat(i)` and `vec(B)=B_(0)sin(kz - omega t)hat(j)`.
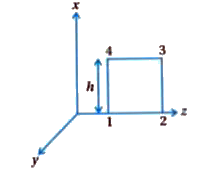
By using similar process and the equation `int vec(B).vec(d)l = mu_(0)I+ in_(0)(d phi_(E ))/(dt)`, prove that `c=(1)/(sqrt(mu_(0)in_(0)))`
View SolutionA plane EM wave travelling along z - direction is desctribed `vec(E )=E_(0)sin(kz - omega t)hat(i)` and `veC(B)=B_(0)sin (kz - omega)hat(j)`. Show that
The average energy density of the wave is given by `U_(av)=(1)/(4)in_(0)E_(0)^(2)+(1)/(4).(B_(0)^(2))/(mu_(0))`.
View SolutionA plane EM wave travelling along z - direction is desctribed `vec(E )=E_(0)sin(kz - omega t)hat(i)` and `veC(B)=B_(0)sin (kz - omega)hat(j)`. Show that
The time averaged intensity of the wave is given by `I_(av)=(1)/(2)c in_(0)E_(0)^(2)`.
View Solution
SECTION C NCERT EXEMPLAR SOLUTION (Long Answer Type Questions) questions and complete solutions for chapter ELECTROMAGNETIC WAVES of KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) of Class 12
All Exercises from KUMAR PRAKASHAN Class 12 PHYSICS ELECTROMAGNETIC WAVES
- BOARD.S QUESTION PAPER MARCH - 2020 (PART - A)
- BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - A
- BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - B
- BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
- SECTION A QUESTIONS - ANSWERS (TRY YOURSELF)
- SECTION A QUESTIONS - ANSWERS (INTRODUCTION)
- SECTION B NUMERICALS (Numerical From .DARPAN. Based On Textbook)
- SECTION B NUMERICALS (Numerical From Textual Exercise)
- SECTION B NUMERICALS (Numerical From Textual Illustrations)
- SECTION C NCERT EXEMPLAR SOLUTION (Long Answer Type Questions)
- SECTION C NCERT EXEMPLAR SOLUTION (Multiple Choice Questions)
- SECTION C NCERT EXEMPLAR SOLUTION (Short Answer Type Questions)
- SECTION C NCERT EXEMPLAR SOLUTION (Very Short Answer Type Questions)
- SECTION D MULTIPLE CHOICE QUESTIONS (MCQs)
- SECTION D MULTIPLE CHOICE QUESTIONS (MCQs) MCQs asked in Competitive Exams