A plane EM wave travelling along z - direction is desctribed →E=E0sin(kz−ωt)ˆi and veC(B)=B0sin(kz−ω)ˆj. Show that
The average energy density of the wave is given by Uav=14∈0E20+14.B20μ0. Solution in Gujrati
In electromagnetic waves due to electric field vector magnetic field vector waves carry energy →E and →B varies with time nad position.
Let E and B is average value at given time,
UE=12∈0E2 and energy density due to magnetic field B,
UB=12B2μ0
Total average energy density of EM waves,
Uaverage=UE+UB=12E0E2+12B2μ0
Consider EM wave propagating in z - direction hence electric field and magnetic field will be represented as
→E=E0sin(kz−ωt) and
→B=B0sin(kz−ωt)
Average value of E2 over one cycle (periodic time)
<E2>=E202
Hence Uaverage=12E0E202+12μ0(B202)
So, Uaverage=14[∈0E20+E204μ0] ...(1)
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SECTION D MULTIPLE CHOICE QUESTIONS (MCQs)76videos
ELECTROMAGNETIC WAVES
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SECTION D MULTIPLE CHOICE QUESTIONS (MCQs) MCQs asked in Competitive Exams23videos
ELECTROMAGNETIC WAVES
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SECTION C NCERT EXEMPLAR SOLUTION (Short Answer Type Questions)9videos
ELECTROMAGNETIC WAVES
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )38videos
ELECTROMAGNETIC INDUCTION
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section D ( MCQs asked in Cometitive Exams )39videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
Similar Questions
Maxwell's equations describe fundamental laws of …..
01:50View SolutionMaximum value of magnetic field of progressive electromagnetic wave is 20 nT, then maximum value of electric field is ………
08:55View SolutionShow that the magnetic field B at a point in between the plates of a parallel plate capacitor during charging is B=μ0∈0r2.dEdt (symbols having usual meaning).
 03:14View Solution
03:14View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......
 02:28View Solution
02:28View SolutionCapacitance of a capacitor 100 μ F. The work is done for depositing chargc 8×10−18 C on it will be .........
02:48View Solutionif E=E_(0)sin(kz-omegat) and B=B_(0)(kz-omegat) are electric and magnetic field produced by an electromagnetic wave travelling in +z direction in a medium. Then if eta=(E_(0))/(B_(0)) , then the value of eta is [mu =permeability of a medium epsilon= permittivity of medium]
02:38View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E_(0) " sin "(kz- omegat) hati " and " B =B_(0) " sin " (kz- omegat) hatj (i) Evaluate intE. dl over the rectangular loop 1234 shown in figure. (ii) Evaluate int B.ds over the surface bounded by loop 1234. (iii) Use equation int E.dl = (-dphi_(B))/(dt) to prove (E_(0))/(B_(0)) =c. (iv) By using similar proces and the equation int B.dl =mu_(0) I+ epsilon_(0) (dphi_(E))/(dt), prove that c (1)/(sqrt(mu_(0) epsilon_(0))
01:54View SolutionThe magnetic field of a plane electromagnetic wave is given by: →B=B0ˆi−[cos(kz−ωt)]+B1ˆjcos(kz+ωt) where B0=3×10−5T and B1=2×10−6T. The rms value of the force experienced by a stationary charge Q=10−4C at z=0 is close to:
03:06View SolutionA. The electric field of a plane electromagnetic wave travelling in the +ve Z - direction is described by
a. Ex=E0sin(kz+ωt)
b. Ex=E0sin(kz−ωt)
c. Ex=E0sin(2kz)
d. Ex=E0sin(kz)
B. We feel excessive sweating on a cloudy day. Why ?05:00View SolutionAn electromagnetic wave travels in vacuum along z - direction : →E=(E1ˆi+E2ˆj)cos(kz−ωt). Choose the correct options from the following :
01:48View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . Evaluate int vec(E ). Vec(d)l over the rectangular loop 134 shown in figure.
13:58View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . Evaluate int vec(B).vec(d)s over the surface bounded by loop 1234.
04:35View SolutionA plane EM wave travelling in vacuum along z - direction is given by →E=E0sin(kz−ωt)ˆi and →B=B0sin(kz−ωt)ˆj.
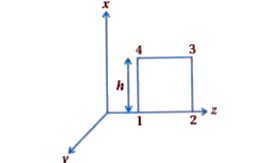
Use equation ∫→E.→dl=−dϕBdt to prove E0B0=c.View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . By using similar process and the equation int vec(B).vec(d)l = mu_(0)I+ in_(0)(d phi_(E ))/(dt) , prove that c=(1)/(sqrt(mu_(0)in_(0)))
06:05View SolutionA plane EM wave travelling along z - direction is desctribed →E=E0sin(kz−ωt)ˆi and veC(B)=B0sin(kz−ω)ˆj. Show that
The time averaged intensity of the wave is given by Iav=12c∈0E20.View Solution

