Complete Solutions to प्रश्नावली 10(B) of chapter सदिश बीजगणित of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सदिश बीजगणित |
| MANOHR RAY | प्रश्नावली 10(B) |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
किसी मूल बिंदु के सापेक्ष A और B बिंदुओं के स्थिति सदिश क्रमशः `veca` और `vecb` है तो (i) `vec(AB)`, (ii) `vec(BA)` सदिशों को ज्ञात करो।
View Solution(a) निम्न चित्र में त्रिभुज ABC में सदिश `vec(AB)` तथा `vec(BC)` का योगफल ज्ञात कीजिए।
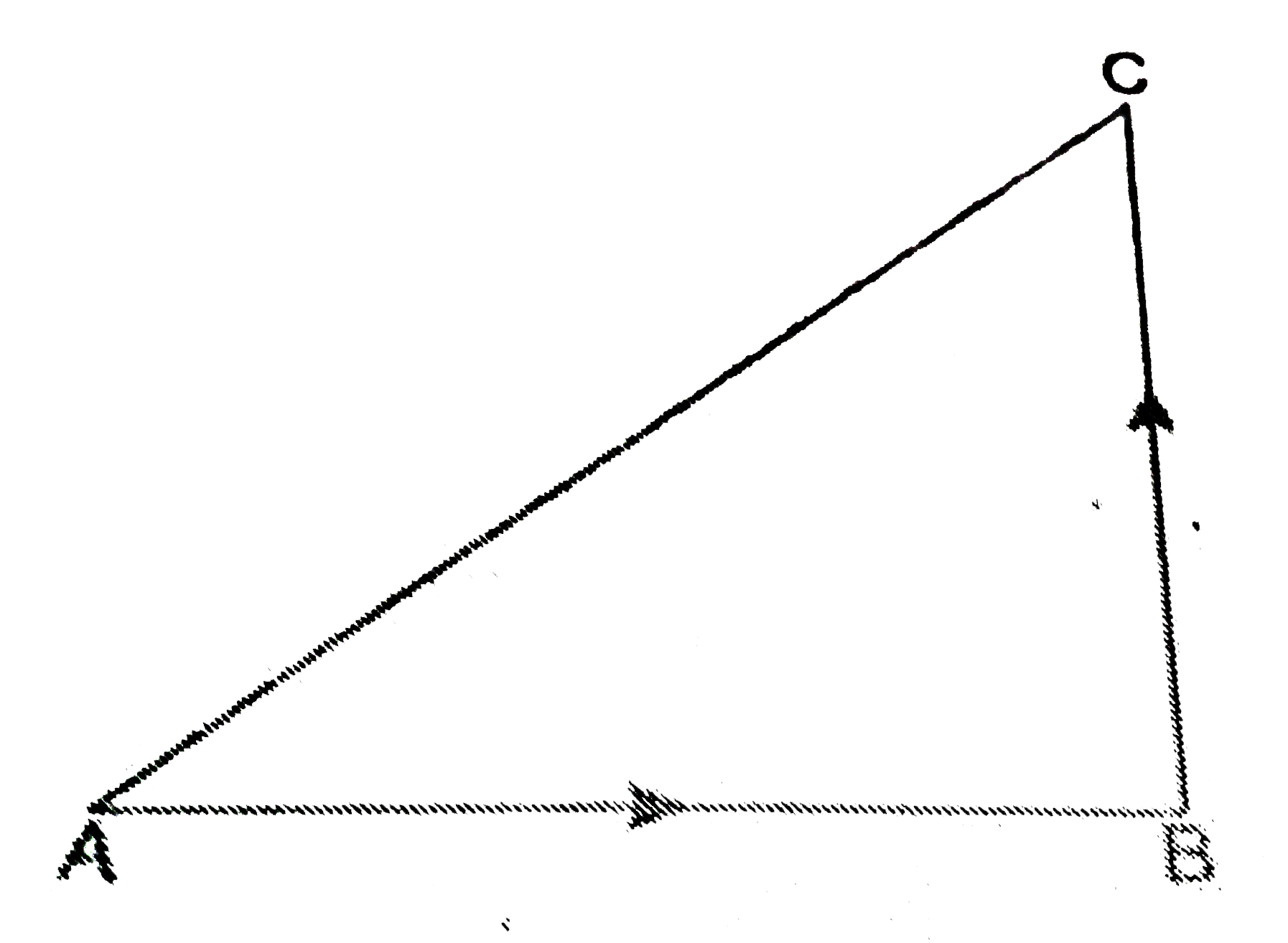
(b) निम्न चित्र में `vec(OA)+vec(OB)` ज्ञात कीजिए।

(c) `DeltaABC` में क्रमशः `vec(AB),vec(BC),vec(CA)` से निरूपित सदिशों का योग कितना है?
View Solutionदिए गए चित्र में `vec(OA)=veca,vec(AB)=vecb` तो `vec(OB)` और `vec(CD)` ज्ञात करो जबकि C,D क्रमशः `OA` और `AB` के मध्य बिंदु है।
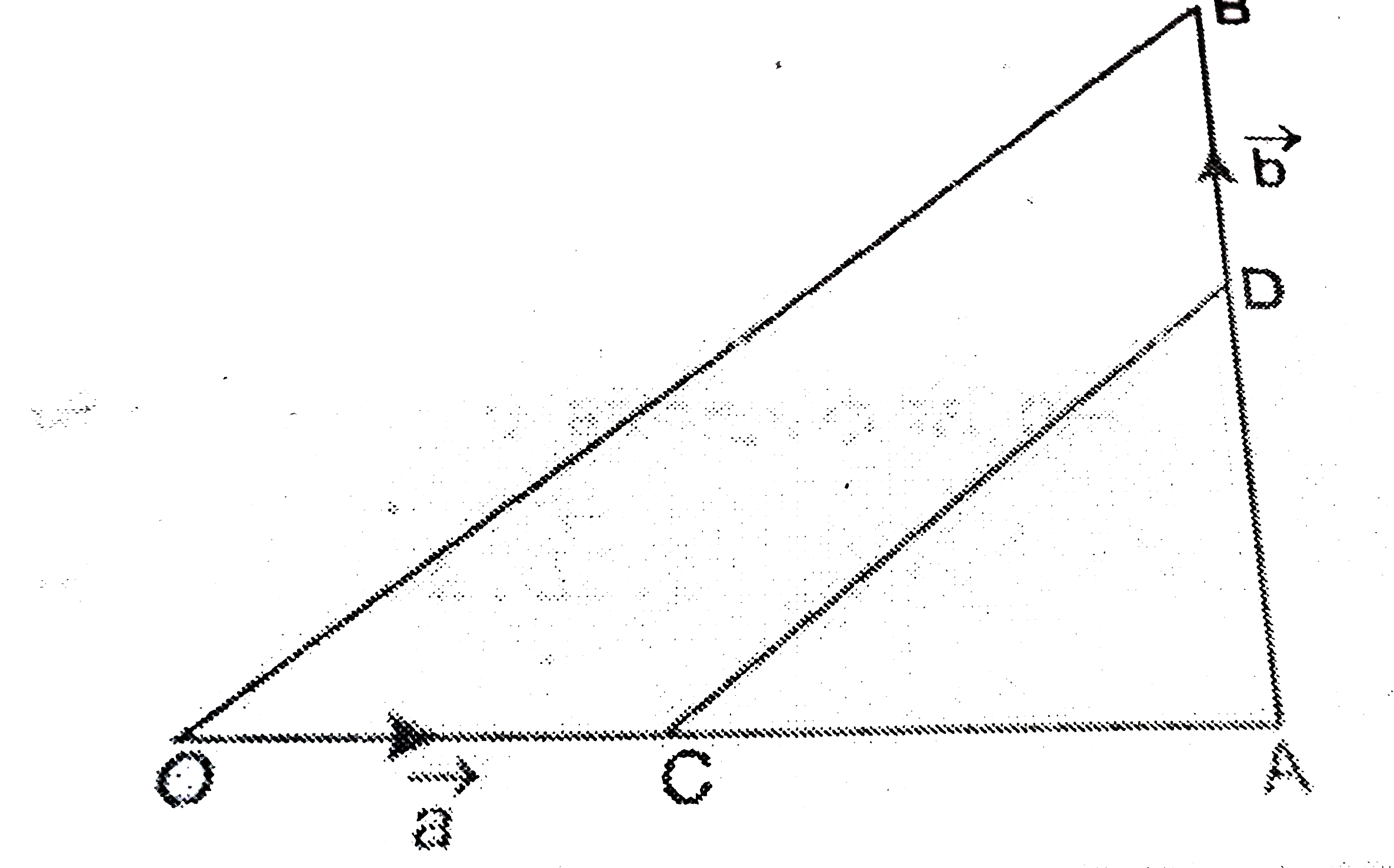
View Solution(i) निम्न चित्र से `vec(AD),vec(DA)` सदिश ज्ञाम करो। (ii) यदि `vec(AB)=veca,vec(BC)=vecb,vec(AD)=vecc,` तो `vec(DC)` ज्ञात करो।

View Solutionनिम्न चित्र में सदिश `vec(CB)` का मान बताइए।

View Solution`ABCD` समांतर चतुर्भुज है। E,AB का मध्य बिंदु है और F,BC का मध्य बिंदु है। यदि `vec(AB)=veca` और `vec(AD)=vec(b)` तो `vec(EF)` का मान बताओ।

View Solutionतीन सदिश `veca,vecb,vecc` इस प्रकार हैं कि `veca+vecb+vecc=0` तो दर्शाइए कि ये सदिश एक त्रिभुज निर्मित करते है।
View Solution`ABCD` कोई समांतर चतुर्भुज है। सिद्ध कीजिए कि रेखाओं `vec(AB),vec(CD),vec(AC)` और `vec(DB)` के द्वारा निरूपति बलों का परिणामी बल `2vec(AB)` के द्वारा मान, दिशा और स्थिति में निरूपित होगा।
View Solutionएक समतल में चार बिंदु `A,B,C,D` है तो `vec(AB)+vec(BC)+vec(DC)+vec(DA)` का मान ज्ञात कीजिए।
View Solutionएक समतल में चार बिंदु A,B,C,D है और चार सदिश रेखाएं `AB,BD,DC` और `CA` के द्वारा निरूपित की जाती है तो सिद्ध कीजिए कि `vec(AB)+vec(BD)+vec(DC)+vec(CA)=0`
View Solution`ABCD` एक समांतर चतुर्भुज है। `E` और `F` क्रमशः CD और AD के मध्य बिंदु हैं। `vec(BE),vec(BF)` को `vec(BA)` और `vec(BC)` के पदों में व्यक्त करो।
View Solution`ABCDEF` एक समषट्भुज है जिसमें `A` पर `vec(AB),vec(AC),vec(AD),vec(AE)` तथा `vec(AF)` बल कार्य करते हैं, तो सिद्ध कीजिए कि उनका परिणामी `3vec(AD)` है।
View Solutionयदि एक समषट्भुज की दो आसन्न भुजाओं से निरूपित सदिश `veca` और `vecb` हो तो क्रमशः अन्य भुजाओ से निरूपित सदिश क्या है?
View Solution`ABCDE` एक पंचभुज है। सिद्ध कीजिए कि बलों `vec(AB),vec(AE),vec(BC),vec(DC),vec(ED)` और `vec(AC)` का परिणामी `3vec(AC)` है।
View Solution`ABCD` एक चतुर्भुज है और AC और BD इसके विकर्ण हैं । सिद्ध करो कि सदिश `vec(AB)+vec(DC)=vec(AC)+vec(DB)`
View Solution`ABC` एक त्रिभुज है। भुजा BC का मध्य बिंदु `D`है। सिद्ध कीजिए कि `vec(AB)+vec(AC)=2vec(AD)`.
View Solutionयदि `vec(AB)` का मध्य बिंदु `C` है तथा `AB` के बाहर कोई बिंदु `P` है तो सिद्ध कीजिए कि `vec(PA)+vec(PB)=2vec(PC)`.
View Solution
प्रश्नावली 10(B) questions and complete solutions for chapter सदिश बीजगणित of DR HARSWAROOP SHARMA MATHS (HINDI) of Class 12